富水高压隧道掌子面涌突水稳定性研究
2021-07-14管连永尚明源李化云
管连永,尚明源,李化云
(1.四川路航建设工程有限责任公司,四川 成都 610041;2.核工业西南勘察设计研究院有限公司,四川 成都 610031;3.西华大学土木建筑与环境学院,四川 成都 610039)
在富水地层修建隧道易引起山体内贮藏的大量地下水通过掌子面涌入隧道,造成人员伤亡、冲毁施工机具,造成巨大损失。师晓权[1]基于极限平衡原理建立掌子面稳定分析水平条分模型,引入了掌子面锚杆加固等效压力系数ka,能较为准确模拟掌子面锚杆加固效果。耿萍等[2]利用离散元方法,追踪统计了隧道周围岩体的裂隙发育、隧道内的突水量和突泥量,揭示了隧道涌水突泥随断层倾角变化的规律:富水断层倾角越小,隧道与断层的竖向距离越小,隧道越容易发生涌水突泥,掌子面底部为易发位置。金建伟[3]研究了海底隧道结构防排水原则、排放量标准,并给出了建立厦门翔安海底隧道防排水体系的建议。包德勇[4]通过工程实例研究了富水隧道在断层破碎带突涌水的特征及原因,并给出了相应的工程对策。Chambon 等[5]对砂性土体隧道掌子面稳定性进行研究,描述了不同埋深情况下掌子面的坍塌形式,强调了掌子面稳定性与未支护段有密切关系。王秀英等[6]基于极限平衡理论,采用水平条分法推导了掌子面极限支护力计算公式,求解了试验段浅埋情况下所需的掌子面支护力。梅卫锋等[7]推导了突泥突水情况下隧道掌子面岩墙厚度的计算公式,根据隧道已有的力学参数,计算了不同溶腔压力作用下,隧道掌子面前方岩墙的最小安全厚度。王秉勇等[8]推导出浅埋长距离隧道掘进施工中掌子面稳定性的计算公式。顾博渊等[9]在基于楔形块体理论对掌子面稳定性进行分析的基础上,得到一种分析隧道掌子面稳定性的简化方法。郑明新等[10]采用有限元软件MIDAS/GTS 模拟上下台阶法开挖,研究掌子面失稳机制及需采取的应对措施,并提出8 种掌子面加固方案。杨为民等[11]通过对比隧道前方有、无溶洞条件下开挖工况,从位移、应力、塑性区3 个方面分析了隧道前方大型溶洞对隧道围岩稳定性的影响。
综上所述,虽然有研究取得了诸多成果,但主要是针对掌子面失稳破坏的机制、破坏形式做出相应研究,未能探明富水高压工况下保障掌子面稳定的极限条件。基于此,本文旨在通过研究富水隧道开挖过程,在探明掌子面失稳过程的同时,提出确保掌子面稳定的极限防突体厚度(掌子面与断层破碎带之间的距离),以此来判别掌子面掘进至断层破碎带附近的加固时机。
豹狸岗隧道位于峨眉市金口河区,左线全长3 650 m,右线全长3 603 m,均为特长隧道。设计中隧道穿越多条富水高压裂隙密集带,极易发生突泥涌水,隧道掌子面接近裂隙密集时,可依据本研究成果指导施工,保障隧道顺利通过。
1 流固耦合机制及突泥涌水发生机制
1.1 流固耦合机制
岩土体中水的渗流场改变会引起应力场相应变化,致使岩土体渗透变形,这一过程具有一定的时效性,该水渗流场对应力场的影响主要表现在两个方面:1)水的渗流对裂隙结构面的物理化学作用,减弱结构面填充物的物理力学性质,降低了结构面的强度;2)地下水通过水力作用于结构面而产生扩展的作用。水在岩土体中尺寸、形状十分不规则的孔隙或岩体裂隙、溶洞中流动[12]。我们难以得到水在岩土体空隙或者裂隙中的运动规律。介于此,可采用平均的概念进行描述,研究具有等效的平均性质的渗透规律。经过对比分析表明,将岩土体假设为连续介质,可以完全满足实际工程精度的要求。
1.2 隧道突泥涌水发生机制
隧道岩体破坏的根本原因在于地下水,其对岩石有着物理、化学以及力学作用。它通常会引起:1)岩石软化从而导致岩体及结构面强度下降,在裂隙面和结构面起润滑作用导致摩阻力减小,增加岩块的活动自由度,从而使得岩体加速向破碎–松散介质转化,促进岩体强度和变形特性的根本变化。2)增大岩体裂隙的连通性,并扩大其张开度,使得其赋水导水能力增强,使渗流场变化对岩体稳定性和应力场的影响增大。3)由于地下水的存在,在其静水压力和动水压力的作用下,岩土体原来的渗流场和应力场发生改变,并保持着动态平衡。隧道开挖通常会导致这种平衡破坏,当其中一方变化幅度过大,这种动态平衡将被打破,触发诸如滑塌、涌水等地质灾害。水槛动态剧变通常反映工程体应力环境的恶化。
2 模型假定及物理力学参数
本节采用有限差分数值模拟软件Flac3D,模拟豹狸岗隧道穿越裂隙密集带的过程,研究掌子面失稳过程,确定掌子面极限防突体厚度。对于正常围岩的渗透性,其表现为各向同性,x、y、z三个方向的渗透系数一致(kx=ky=kz);裂隙密集带的围岩由于有较强的方向性,其渗透性表现为各向异性,其中x、y方向的渗透系数一致,z方向的渗透系数较大(kx=ky<kz)。渗透系数的设置情况如图1 所示。具体的物理力学参数见表1,围岩及支护的渗透系数见表2。
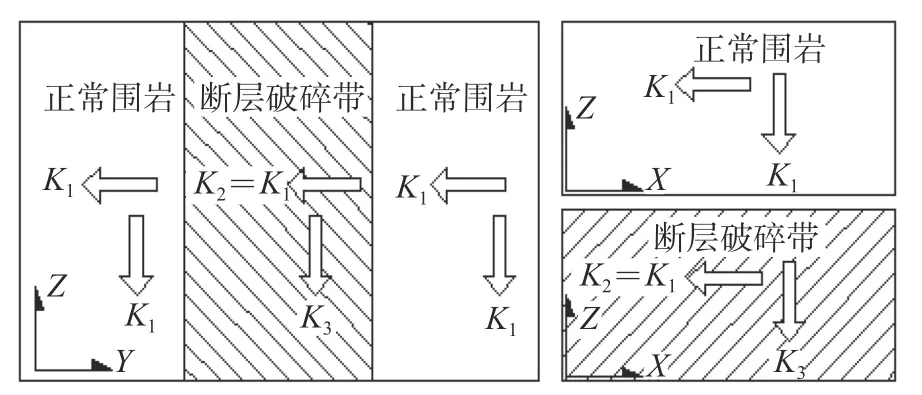
图1 渗透系数设置

表1 围岩及支护结构参数

表2 渗透系数
本文通过建立三维有限差分模型,模拟实际开挖,建立掌子面失稳模式,研究失稳过程,确定掌子面极限防突体厚度。
建立模型如图2 所示。模型尺寸范围:−50 m ≤x≤50 m,0 m ≤y≤60 m,−28 m ≤z≤70 m,Z方向的零点位置为隧道中心。

图2 模型示意图
隧道净空等效半径6.120 m,初支为喷射混凝土,厚0.24 m,二衬钢筋混凝土厚度50 cm。模型尺寸范围:−50 m ≤x≤50 m,0 m ≤y≤60 m,−28 m ≤z≤70m。
纵向围岩分布:正常围岩范围为0 m ≤y≤24 m、40 m ≤y≤60 m;裂隙密集带围岩范围为24 m ≤y≤40m。隧道中心的水头高度:H=60 m。
为了模拟施工中掌子面逐渐逼近裂隙密集带而发生的失稳现象,模型沿纵向的开挖步骤与施工保持一致,开挖进尺为2 m 一个循环。初期紧跟掌子面,二次衬砌滞后于掌子面。
3 掌子面失稳破坏演化过程分析
本节对地层渗流场随隧道施工的变化规律进行分析。由于开挖后,掌子面及周边临空面的渗流边界改变,初始的渗流场所处的平衡状态被打破,渗流场需要重新分布。地层的孔隙水压力随隧道开挖的变化过程如图3—图5 所示。

图5 开挖30 m 时的水压值(单位:Pa)
对围岩空隙水压演化过程进行分析,将掌子面失稳破过程分为3 个阶段:
1)孕育阶段。如图3 所示,沿隧道纵向,由掌子面开挖引起的围岩荷载变化导致掌子面后方的防突体出现超空隙水压力现象。该现象随开挖面逼近裂隙密集带越发明显,裂隙密集带区域的孔隙水压力值受隧道开挖影响较小。掌子面处于稳定状态。
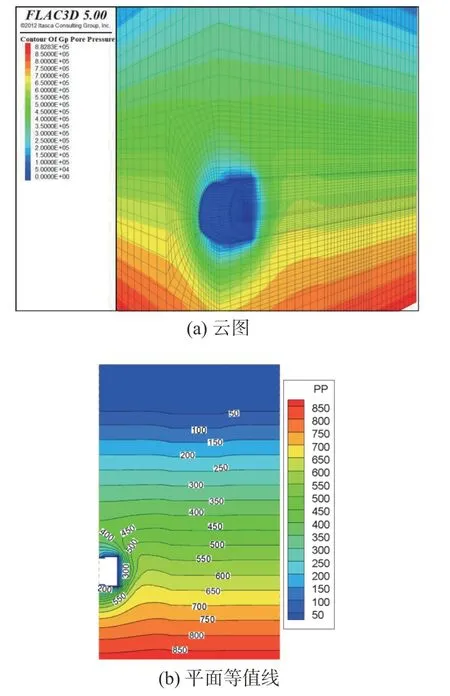
图3 开挖6 m 时的水压值(单位:Pa)
2)释能阶段。如图4 所示,随着进一步开挖,掌子面与裂隙带间距不断减小,虽然未穿过裂隙带,但是由于隧道掌子面临空及排水,而使裂隙带积压的高水压和掌子面之间形成了一定的联通作用,超孔隙水压力现象减弱直至消失,裂隙带的水压得到一定程度释放。由于水力作用,掌子面仍处于敏感状态。当防突体厚度无法承受高水压和高地压的联合作用时,涌水现象就会发生。
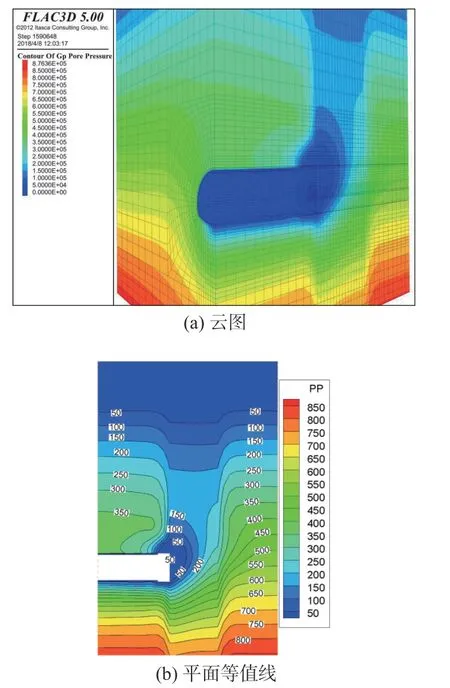
图4 开挖24 m 时的水压值(单位:Pa)
3)发生阶段。如图5 所示,由于防突体过于薄弱,无法承受水压,裂隙带和隧道之间的流水“管道”被打通,裂隙带积水通过掌子面涌入隧道,可以初步判定此时掌子面前方的防突体失效。从此过程中可以看出,在裂隙带水侵入隧道后,裂隙带水头在空间上形成一个漏斗的形式。在这个漏斗之内地层孔隙水压力值为一个极低值,可以称这个空隙水压低值区为“泄水漏斗”。而掌子面产生失效的断面和裂隙带之间的距离,称之为“临界失效距离”,在这个距离之外为安全开挖距离。
超静孔隙水压力是由于外部作用或者边界条件变化在岩体中引起的不同于静孔隙水压力的那部分孔隙水压力。在有排水条件下,它将逐渐消散,并在消散过程中伴随岩体的体积变化。
4 防突体极限厚度的分析确定
本节分别用掌子面挤出位移、涌水量、塑性区体积及最大剪切应变增量4 个指标采用切线法对极限防突体厚度进行了确定(见图6—图9)。以图6 为例,以掌子面掘进位置为横坐标,掌子面涌水量为纵坐标绘制曲线。由曲线走势可知,20<x<24 之间存在一拐点,掌子面在该点处于极限稳定状态。通过做切线确定两条切线的交点x坐标,该点到裂隙密集带的距离为极限防突体厚度。防突体极限厚度如表3 所示。
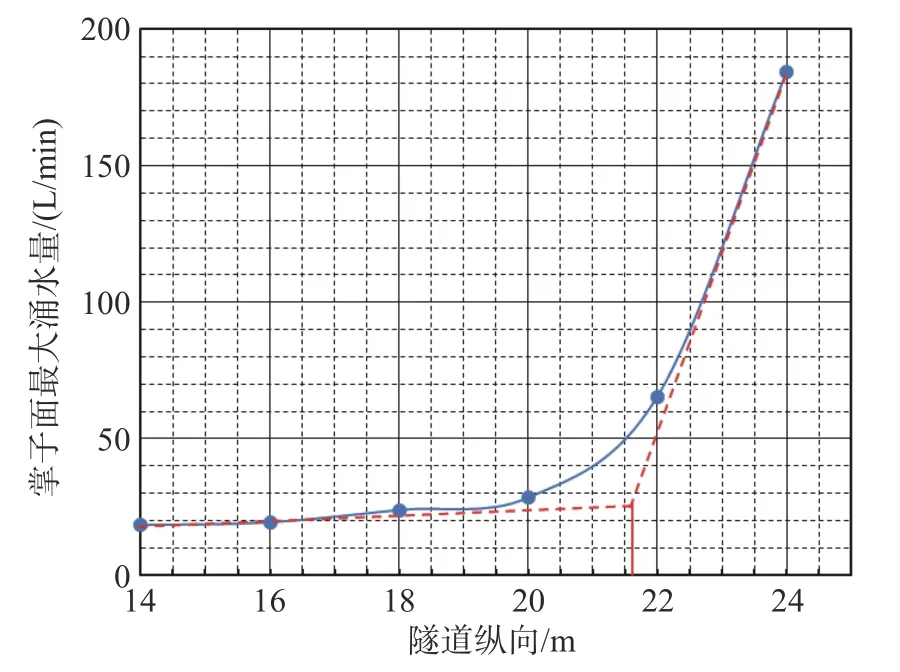
图6 涌水量判定极限防突体厚度
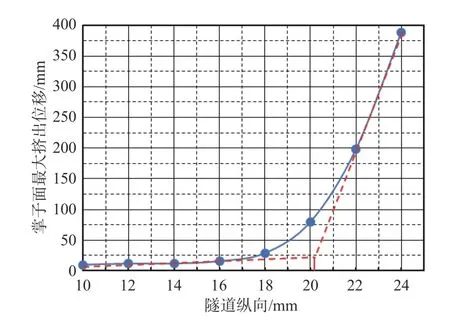
图7 掌子面位移判定极限防突体厚度
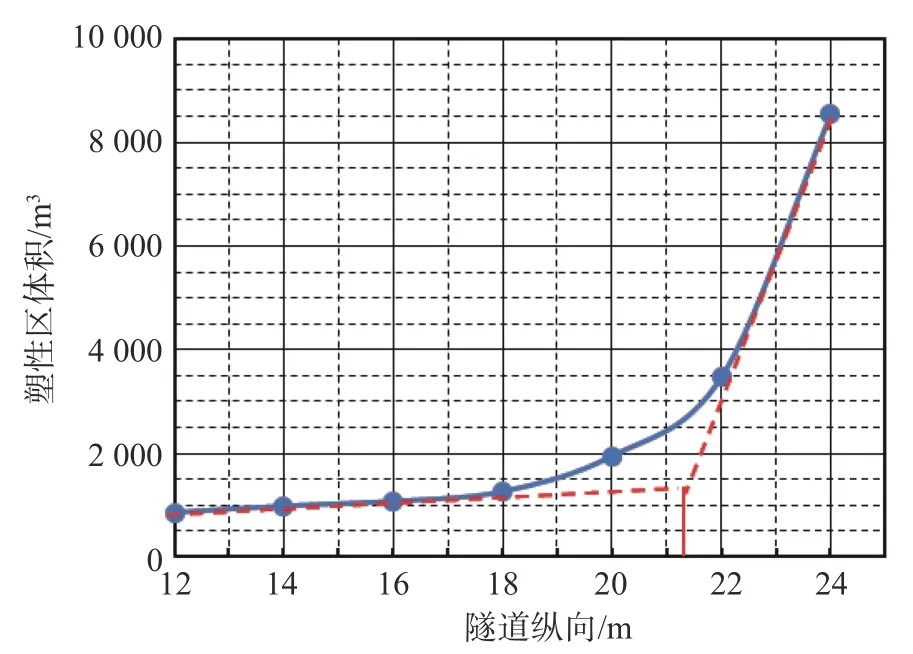
图8 塑性区判定极限防突体厚度
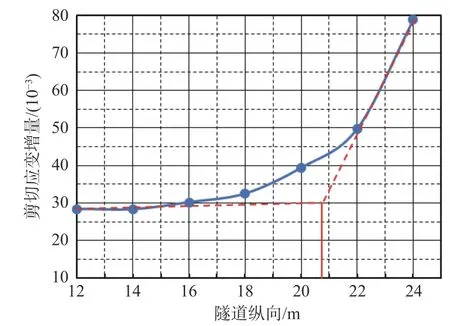
图9 剪切应变判定极限防突体厚度
由表3 可知,4 个指标得到的极限厚度分别为2.4、3.8、2.7、3.3 m,4 个指标得到的结果存在一定的误差。为确保掌子面的稳定性,我们保守的取其中的最大值作为该种工况的防突体极限厚度,即3.8 m。

表3 防突体极限厚度表
5 结束语
本文建立模型研究了富水隧道掌子面失稳模式;基于突水突泥地层掌子面稳定性分析力学模型,探明了掌子面渗透破坏以及失稳过程;提出掌子面稳定性评价方法,明确了防突体极限厚度。
