岩体内应力波传播的研究进展与展望

王 梦， 范立峰

(北京工业大学城市建设学部， 北京 100124)

岩体内应力波传播规律的研究是岩体工程稳定性分析的基础. 天然岩体是由多种矿物组成的特殊材料. 经历各种地质构造运动后，其内部形成了不同尺度的不连续结构面，对岩体的力学特性以及岩体内应力波的传播规律有很大影响[1-7]. Zhao等[8]研究表明，从细观缺陷到宏观节理等不同尺度不连续结构面均会影响应力波传播. 不同尺度的不连续结构面对应力波传播具有不同的作用机理. 细观缺陷会导致应力波产生弥散和衰减，而宏观节理会造成应力波发生透射和反射. 相较单一尺度的细观缺陷岩体和宏观节理岩体内应力波的传播，双尺度不连续结构面岩体内应力波传播规律的研究更加复杂，需同时考虑细观缺陷和宏观节理对应力波传播的共同作用. 近年来，随着深部岩体工程、极地岩体工程的深入开展，岩体内应力波传播还需考虑多场耦合问题. 本文系统总结了细观缺陷岩体、宏观节理岩体、双尺度不连续结构面岩体内应力波传播的分析方法，展望了极端环境下岩体内应力波传播的研究，对岩体工程动态稳定性分析和安全性评估具有重要的意义.

1 细观缺陷岩体内应力波传播规律的研究

岩体是一种复杂的天然介质，如图1所示. 岩体内存在大量的细观缺陷[9]，图2为采用X射线计算机断层扫描(computed tomography，CT)技术观测到的岩体细观缺陷分布图像. 鉴于岩体内存在的细观缺陷会影响应力波传播，席道瑛等[10]试验研究了应力波的传播规律，揭示了应力波的衰减机制. 随后，李祥龙等[11]采用分离式霍普金森杆(split Hopkinson pressure bar，SHPB)试验装置，研究了材料损伤程度对应力波传播的影响. 另外，鞠杨等[12]基于有限元方法，构建了岩石类孔隙介质的三维数值模型，分析了孔隙结构和空间特征对应力波传播特性的影响. 当应力波在细观缺陷岩体内传播时，细观缺陷形状和分布的不规则性显著影响应力波的传播，导致应力波的散射. 因此，波散射理论被普遍应用于研究细观缺陷岩体的动态力学特性及应力波传播规律[13-17]. Mal[18]验证了币形裂纹对应力波的散射作用. Snchez-Sesma等[19]推导了单裂纹下应力波散射的解析解. 随后，Krüger等[20]利用旋转交错网格，将单裂纹应力波散射的解析解推广到多裂纹介质中. 波散射理论通常假设单一细观缺陷对应力波的滤波效果是相同的，并且适用于细观缺陷在岩体内分布稀疏的情况[21]. 然而，细观缺陷在岩体内通常具有数量多、无序等特点，对于细观缺陷密集分布的真实岩体，波散射理论研究难以得到有效的解析解. 因此，Pointer等[22]采用间接边界元法模拟了任意数量裂隙中散射的地震波. 该方法被Iturrarán-Viveros等[23-24]推广到研究二维和三维裂纹中应力波的散射问题. Chen等[25]结合边界元法和线性滑动边界条件，进一步模拟了二维裂纹中水平剪切(shear horizontal，SH)波的散射.

图1 天然岩体Fig.1 Natural rock mass

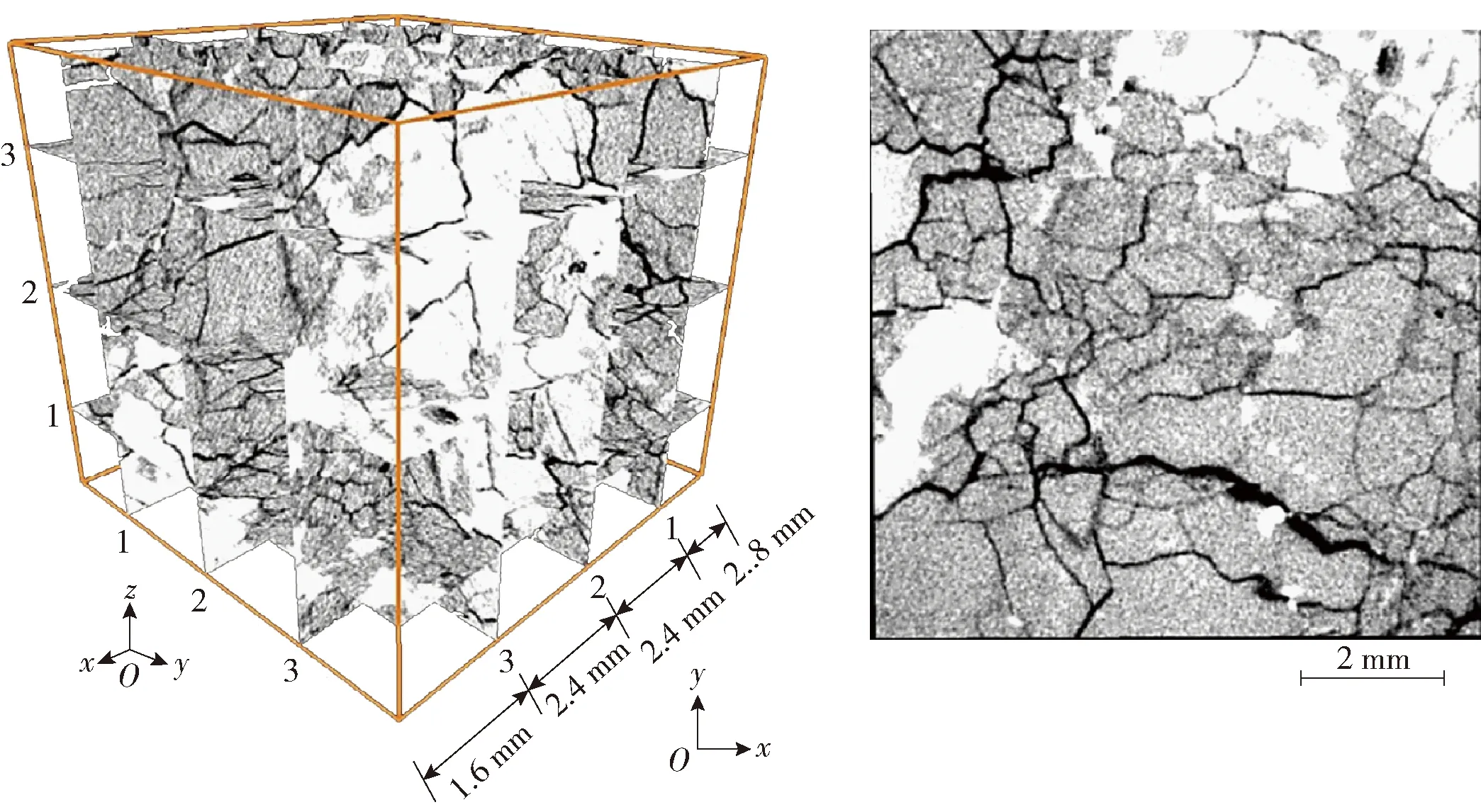
图2 岩体内细观缺陷的CT图像[9]Fig.2 CT images of micro-defects in rock mass[9]

由于天然岩体内通常存在密集分布的细观缺陷，导致应力波传播问题的解析解难以求解. 因此，等效弹性模量方法被提出用来研究细观缺陷岩体内应力波的传播. 等效弹性模量方法将细观缺陷岩体等效地看作连续均匀的介质，通过等效弹性模量建立实际细观缺陷岩体和等效介质模型之间的联系，利用等效弹性模量来反映细观缺陷对岩体内应力波传播的影响[26-30]，通过求解等效介质内应力波的传播规律来表征实际细观缺陷岩体内应力波的传播规律，从而建立细观缺陷岩体与应力波传播速度和幅值衰减的关系. 为了更全面地描述岩体的力学性质，有必要考虑细观缺陷的大小、密度和细观缺陷填充物(气体、液体、断层泥等)的性质对等效弹性模量的影响. 因此，一阶理论[31-32]、自洽理论(self-consistent)[33-36]、微分自洽理论[37-40]、滤波法(二阶理论)[41-43]等一系列的等效弹性模量方法被提出. Eshelby[32]基于一阶理论建立等效弹性模量，研究了含椭圆形的各向同性介质的内外部应力、应变场. 随后，该方法被推广到研究含椭圆形的各向异性的介质[32]和各向异性的裂隙岩体[44-45]. O’Connell等[34]和Budiansky等[35]采用自洽理论计算了干性和部分饱和情况下随机分布裂隙介质的等效弹性模量，分析了介质内微裂隙之间的相互作用. 在此基础上，O’Connell等[36]进一步分析了饱和裂隙介质的等效弹性模量. 为了更精确地预测细观缺陷介质的等效弹性模量，Henyey等[38]提出了微分自洽理论来分析随机分布的币形裂隙介质的等效弹性模量. Zimmerman[39]采用微分自洽理论计算了含球形孔隙或夹杂物岩体的等效弹性模量，并与传统的自洽理论进行了比较. 随后，Hodson[43,46]提出了滤波法研究含定向或随机定向裂纹介质的等效弹性模量，并将滤波法推广到研究裂隙密度无序且含多方向裂隙列介质的等效弹性模量[42].

研究表明细观缺陷岩体在应力波传播作用下具有显著的频率依赖性等动态力学特性[47-49]，而等效弹性模量方法无法考虑此类特性[50]. 因此，等效黏弹性介质方法被提出用来等效研究细观缺陷岩体的动态力学行为[51-53]. Ichikawa等[51]用X射线显微镜观察了花岗岩的三维结构，并采用黏弹性均匀化方法分析了细观缺陷花岗岩的力学行为. Ren等[49]基于数值流行方法模拟了随机分布细观缺陷岩体内应力波的传播，进一步验证了细观缺陷岩体的等效黏弹性特性. Fan等[52]基于应力波传播理论研究了细观缺陷岩体的等效黏弹性行为，采用冲击试验实际测得了细观缺陷岩体的等效复模量，并利用复模量建立了等效黏弹性介质模型，冲击试验的试验装置如图3所示. Niu等[54]通过比较数值计算结果与试验结果，建立了一种确定岩杆黏性系数的有效方法. 基于等效黏弹性连续介质方法，Zhou等[55]采用频谱分析方法计算了细观缺陷岩体内应力波传播的衰减系数和波数，并用数值流行方法模拟了细观缺陷岩体内应力波的传播，数值模型方案如图4所示. 另外，王礼立[56]提出了三特征线时域分析方法，考虑了应力波在黏弹性介质中的传播，计算黏弹性介质中应力波传播的三特征线方法如图5所示. 随后，Wang等[57]和Zhu等[58-59]采用三特征线方法研究了黏弹性介质中的应力波传播特性. 基于黏弹性损伤理论和应力波在一维黏弹性杆中的传播理论，Niu等[60]研究了应力波传播引起的一维黏弹性杆的层裂，得到了可以预测层裂位置、频率、时间的理论方程式. 以上研究均基于常温岩体工程，随着深部、极地等多场环境下岩体工程的开展，高低温岩石力学特性研究已逐渐成为岩石力学的研究热点. 岩体在温度的影响下，其内部构造、物理力学特性等都会发生一系列改变[61-62]. 图6表示不同温度下岩石中的细观缺陷，从图6中可以看到，温度越高岩石中的细观缺陷越多. 因此，温度导致的岩体物理学特性变化必然会影响应力波的传播规律. 研究高低温岩石力学特性对极端环境下岩体工程的发展有重要意义.

图3 冲击试验的试验装置Fig.3 Experimental setup for impact test

图4 细观缺陷岩体内应力波传播的数值模型方案[55]Fig.4 Scheme of numerical model for stress wave propagation through micro-defected rock mass[55]

图5 计算黏弹性介质中应力波传播的三特征线方法Fig.5 Three characteristic lines method for calculating stress wave propagation in viscoelastic media

图6 不同温度下岩石中的细观缺陷Fig.6 Micro-defects in rock under different temperatures

2 宏观节理岩体内应力波传播规律的研究

天然岩体内不仅存在细观缺陷，同时存在大量的宏观节理[63-65]. 岩体内的宏观节理分为填充节理和非填充节理，如图7所示. Myer等[66]研究了应力波在单一节理岩体内的传播规律，图8表明，节理的力学特性显著影响应力波传播. 对于充填节理，大量的试验研究表明[67-69]，填充材料的粒径、含水量以及厚度等都会影响应力波的传播. 对于非填充节理，Li等[70]采用SHPB试验装置，研究了应力波在单个宏观节理岩体内传播的透、反射现象. 另外，Zhu等[71]通过通用离散元程序(unitized digital electronic calculation，UDEC)对应力波在含多个相交节理岩体内的传播进行了数值模拟分析，并与解析解和试验数据进行比较，验证了UDEC研究节理岩体内应力波传播的正确性. 目前，宏观节理岩体内应力波传播规律的理论分析方法主要有位移不连续方法和等效连续介质方法. 其中位移不连续方法可求解单一裂隙或者一组平行裂隙中应力波的传播[72-74]，并且该方法在节理裂隙较少的情况下求解效果较好[75]，因而被广泛应用于研究宏观节理岩体内应力波的传播. 用位移不连续方法求解宏观节理岩体内应力波传播时，假设宏观节理两侧的应力场是连续的，而位移场由于宏观节理本身的变形而不连续[76]. 另外，根据宏观节理的变形特性提出了线性位移不连续方法和非线性位移不连续方法. 当宏观节理位于应力波远场时，通常采用线性位移不连续方法考虑宏观节理的线性变形特性，当宏观节理处于应力波近场或者含填充物时，需要采用非线性位移不连续方法考虑宏观节理的非线性变形特性. 其中，线性位移不连续方法为

图7 岩体内的填充节理和非填充节理Fig.7 Filled and unfilled joints in rock mass

图8 宏观节理对应力波传播的影响[66]Fig.8 Effects of macro-joint on stress wave propagation[66]

(1)

非线性位移不连续方法为

(2)

式中：σ为法向应力；u为宏观节理法向位移；kn为初始宏观节理刚度；dmax为宏观节理最大允许闭合量；上标“-”表示参数属于宏观节理前的波场；“+”表示参数属于宏观节理后的波场.

Mindlin[77]较早地采用位移不连续方法解决了弹性约束板边界处纵波和横波的耦合问题. 随后，Schoenberg[78]和Pyrak-Nolte[79]基于线性位移不连续方法推导出宏观节理岩体内任意入射角度的应力波透、反射系数的解析解. Pyrak-Nolte等[75]采用线性位移不连续方法结合频谱分析方法，研究了应力波在一组平行节理中的传播特性，揭示了宏观节理对应力波的透、反射作用机制. Zhao等[80]采用线性位移不连续方法结合平面波分析和传播矩阵法，进一步研究了任意入射角度下应力波通过多条宏观节理的衰减规律. 对于远场动态荷载，宏观节理通常处于线性变形状态，可采用线性位移不连续方法有效地求解宏观节理处应力波的传播[69,81-82]. 然而对于近场动态荷载，应力波幅值较大，宏观节理会产生非线性变形[68,83-88]，此时必须采用非线性位移不连续方法研究应力波传播[89]. 因此，Bandis等[83]提出了双曲线模型(BB模型)来表示宏观节理的非线性变形特性. Zhao等[90]基于BB模型提出了结合特征线方法的非线性位移不连续方法，研究了大振幅应力波在非线性变形宏观节理处的传播特性，计算了非线性宏观节理处应力波传播的透、反射系数. 宏观节理处应力波传播的透、反射示意图和特征线方法如图9所示. 随后，该方法被扩展到研究一组平行的非线性变形宏观节理中应力波的传播[91]. 俞缙等[92]基于BB模型和经典指数模型建立了不同的位移不连续方法，比较了宏观节理在2种非线性变形行为下对应力波传播规律的影响，并对宏观节理的非线性变形本构关系做了进一步改进[93-96]. 为了揭示斜入射波在非线性变形宏观节理中的传播特性，Li[97]基于非线性位移不连续方法提出了时域递归方法. 针对复杂地层内应力波传播问题，Fan等[98-99]改进了传统的特征线方法，研究了宏观节理两侧波阻抗不同的岩体对应力波传播特性的影响.

图9 宏观节理处应力波传播的透反射示意图和特征线方法[90]Fig.9 Diagram of transmission and reflection and method of characteristic lines of stress wave propagation across a macro-joint[90]

等效连续介质方法也被广泛应用于研究宏观节理岩体内应力波的传播. 等效连续介质方法与研究细观缺陷岩体的等效弹性模量方法类似，都是从整体上将岩体看作连续、均匀、各向异性介质，通过求解等效连续介质内的应力波传播规律来表征岩体内应力波的传播规律，利用等效弹性模量分析岩体内不连续结构面对应力波传播规律的影响. 等效连续介质方法可以便捷、快速地计算应力波在岩体内的传播规律，在岩体工程领域得到了广泛的应用. 该方法可以高效求解岩体内裂隙数量多且分布均匀的情况下应力波的传播[100-102]. Schoenberg[103]基于等效弹性介质方法，提出了等效横观各向同性模型来表征包含一组平行节理的岩体，研究了应力波在多条宏观节理岩体内传播的反射问题. 随后，Amadei等[104]进一步提出了等效横观各向异性模型来研究应力波在宏观节理岩体内的传播规律. 由于等效弹性介质方法无法考虑宏观节理岩体内应力波传播的衰减特性和频率依赖特性，Li等[105]提出了等效黏弹性介质方法，研究了应力波在一组平行节理中的传播，并引入了虚拟波源的概念，解决了等效黏弹性介质方法内应力波的反射问题. 节理岩体和等效黏弹性介质模型如图10所示. Ma等[102]通过与等效弹性介质方法相比较，证明了等效黏弹性介质方法能够有效地计算宏观节理岩体内应力波的传播. Li等[106]改进了现有的等效黏弹性介质方法，计算了应力波在层状岩体内的传播. Fan等[89]通过将宏观节理的非线性变形特性引入到等效黏弹性介质方法，从而进一步拓展了等效黏弹性介质方法，建立了非线性等效黏弹性连续介质方法，研究了应力波在非线性变形宏观节理岩体内的传播规律.

图10 节理岩体和等效黏弹性介质模型示意图[105]Fig.10 Sketches of macro-jointed rock mass and equivalent viscoelastic medium model[105]

3 双尺度不连续岩体内应力波传播规律的研究

岩体内存在的不同尺度不连续结构面如图11所示. 不同尺度的不连续结构面对应力波的衰减具有不同的作用机理. 细观缺陷使应力波产生弥散和衰减，而宏观节理使应力波发生透、反射现象. 因此，难以建立统一模型分析细观缺陷和宏观节理对应力波传播的影响. 徐松林等[107]通过试验研究了双尺度不连续岩体的动态力学行为，揭示了细观缺陷和宏观节理对应力波传播规律的不同作用机理. Fan等[108]采用数值流形方法建模，在统一框架下分析了双尺度不连续岩体的应力波传播特性. 为了从理论上揭示细观缺陷和宏观节理对应力波传播的影响，俞缙等[109]研究了应力波在复杂岩体内的传播，发现岩石的特性和宏观节理都会引起应力波的衰减. Huang等[110]发展了传播矩阵法来研究应力波在黏弹性节理岩体内的传播. Fan等[111]在频谱分析的基础上提出了扩展的位移不连续方法，分析了黏弹性节理岩体内应力波的传播，并且提出一种均匀- 不连续建模思路来研究双尺度不连续岩体的等效黏弹性行为[21]，如图12所示. 另一方面，基于时域分析的应力波传播计算方法也得到了迅速的发展. Fan等[112-113]提出了基于时域分析的分离式三特征线法，如图13所示. 分离式三特征线与位移不连续方法相结合，研究了双尺度不连续岩体内应力波的传播规律. 随后，非线性位移不连续方法被引入到分离式三特征线方法中，研究了双尺度不连续岩体内非线性变形宏观节理对应力波传播的影响[112-113]. 基于时域分析的特征线方法采用了差分方式求解岩体内应力波的传播，避免了复杂的傅里叶变换，可提高计算效率.

图11 应力波在不同尺度的不连续结构面中的传播[8]Fig.11 Stress wave propagation through different scale discontinuities[8]

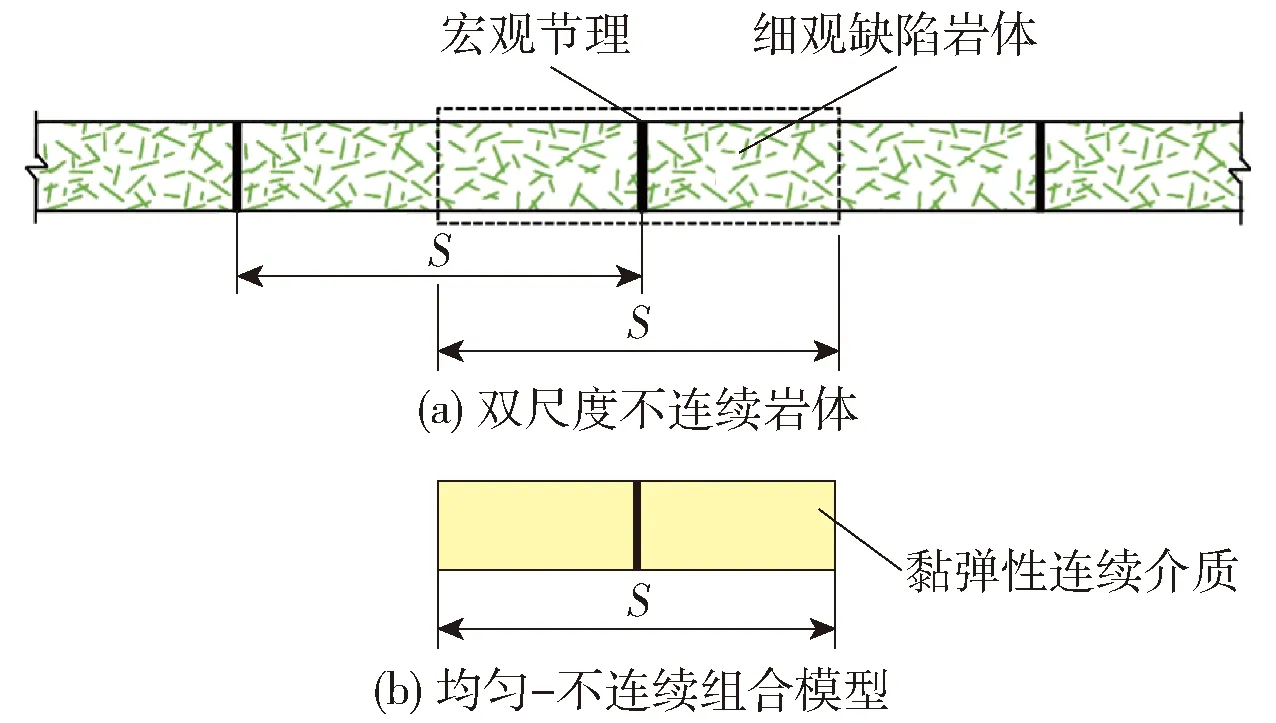
图12 均匀- 不连续组合方法的方案[21]Fig.12 Scheme of the homogenization discontinuity combination approach[21]

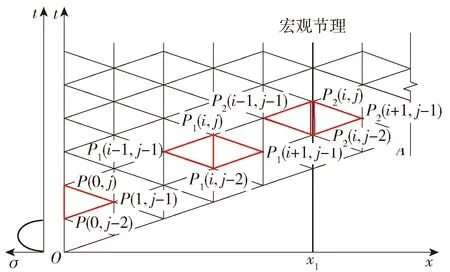
图13 分离式三特征线方法[112]Fig.13 Split three characteristic lines method[112]

4 有待研究的问题

目前，对细观缺陷岩体、宏观节理岩体、双尺度不连续结构面岩体内应力波的传播特性已有广泛的研究，取得了一系列研究成果. 然而，随着川藏铁路、深部工程等国家重大工程的深入开展，岩体工程面临更加复杂的环境，岩体内应力波传播也面临许多新的问题：

1) 对于深部岩体工程，岩体的宏细观内部构造、动态力学响应等均呈现出强非线性特性，如何全面、高效、准备地描述应力波在强非线性特性岩体内的传播规律有待进一步研究.

2) 深部岩体工程处于高温、高压、高地应力的“三高”多场耦合环境，如何分析应力波在“三高”耦合环境下深部岩体工程中的传播规律，揭示高温、高压、高地应力对应力波传播规律的耦合作用机理，是深部岩体工程动态稳定性分析急需解决关键难题之一.

3) 随着川藏铁路、深部岩体工程等国家重大工程的开展，如何在现有应力波传播理论基础上，结合国家重大工程，提出面向实际工程需求的岩体工程动态稳定性分析方法，是机遇也是一种挑战.