考虑模型误差的ROV抗饱和控制设计
2021-07-14薛乃耀王冬姣叶家玮
薛乃耀, 刘 鲲, 王冬姣, 叶家玮
考虑模型误差的ROV抗饱和控制设计
薛乃耀, 刘 鲲, 王冬姣, 叶家玮
(华南理工大学 土木与交通学院, 广东 广州, 510640)
为研究新型有缆开架式遥控水下航行器(ROV)的轨迹跟踪问题, 在径向基神经网络滑膜控制律基础上, 考虑推力约束条件, 提出一种变增益抗饱和辅助系统, 并通过李雅普诺夫稳定性相关定理证明了控制系统的稳定性。该系统充分考虑了ROV的实际作业工况, 利用MARLAB Simulik搭建仿真平台, 在轨迹跟踪仿真验证中引入建模误差、海流干扰、脐带缆作用力等因素影响。仿真结果表明, 加入抗饱和系统后, ROV进行轨迹跟踪时推进系统推力饱和持续时间降低27%, 各自由度的累计跟踪误差降低, 垂荡和横摇方向的跟踪误差大幅减少, 验证了新控制律的可靠性。
遥控水下航行器; 推力饱和; 轨迹跟踪; 径向基神经网络; 滑模控制
0 引言
自20世纪50年代开始, 遥控水下航行器(re- mote operated vehicle, ROV)被用于鱼雷及导弹回收等危险作业任务, 此后更被广泛用于深水探测、水下施工维护工程、钻井作业等领域[1]。ROV结构紧凑, 推进器输出动力有限, 精确的动力学模型和水下环境条件不易获得。为使ROV顺利完成作业任务, 研究人员对ROV在复杂环境下的轨迹跟踪进行了大量研究。自适应鲁棒控制律、最优控制、反馈线性化方法等都被用于解决ROV的轨迹跟踪问题[1-3]。滑模控制和其他智能控制方法因为其抗扰和自适应能力强而在ROV控制中得到应用。朱琦[4]采用准滑模控制方法, 实现ROV的姿态镇定和物体抓取任务; Chu等[5]设计了自适应模糊滑模控制器, 采用模糊系统估计未知非线性影响, 通过自适应更新律处理建模误差和输入饱和问题。基于径向基(radial basis function, RBF)神经网络具有逼近任意非线性函数的能力[6], 将这种性能应用于ROV的运动控制中, 能使其具有很强的抗干扰能力。夏俊[7]通过RBF神经网络自适应控制, 实现了水面无人艇的轨迹跟踪控制。
结合文献[8], 文中设计了一种新型ROV轨迹跟踪控制律。控制初期, ROV与目标轨迹偏差较大, 神经网络权值的学习尚未收敛, 容易导致其推进器处于饱和状态, 影响目标跟踪性能, 并可能使ROV失控。因此, 文中考虑ROV水动力特性、建模误差、海流干扰和脐带缆作用力等因素影响, 采用RBF神经网络设计了神经网络滑模控制器, 完成一种新型ROV轨迹跟踪控制任务。将滑模函数引入辅助系统的状态变量更新律中, 提出了一种变增益抗饱和辅助系统, 通过反馈补偿抑制推进器饱和。并通过合理配置抗饱和系统的增益, 有效提高ROV控制系统稳定性, 保障了RBF神经网络滑模控制律在控制初期且存在推力限幅情况下的轨迹跟踪性能。
1 ROV动力学模型
基于SNAME对海洋航行器运动的定义, 在固定坐标系中, ROV的动力学方程可表示为[8]

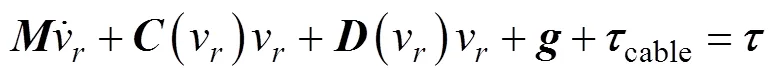




图1 ROV及其坐标系(1~6为螺旋桨编号)
2 控制律设计
2.1 神经网络滑模控制
在滑模控制中, 滑模面定义为

其中


结合ROV的动力学模型, 基于模型的滑模控制律为

ROV动力学模型的获取存在一定的误差, 且其水动力系数影响因素复杂, 采用RBF神经网络对ROV所受的集总扰动进行拟合和补偿, 其对集总扰动的最佳估计为
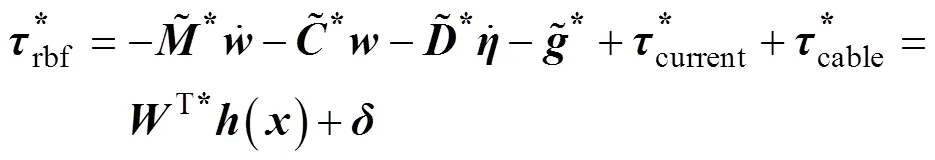


2.2 抗饱和辅助系统设计
为消除推力限幅的影响, 且避免在系统控制律设计中引入辅助系统的跟踪误差, 参考Chen等[10]对输入受限的多输入多输出系统控制设计, 建立以下辅助系统

辅助系统补偿控制力为

当系统在神经网络控制律作用下出现推力饱和时, 通过辅助系统生成补偿信号, 抵消饱和推力。辅助系统更新律式(12)考虑了系统与期望轨迹的状态误差对控制输出的影响, 在辅助系统状态更新律中引入滑模函数, 从而在控制起始, 状态误差偏大时, 结合系统状态, 动态地调整饱和反馈补偿, 更为有效地抑制推力饱和。
此时ROV在固定坐标系下输出的推力为
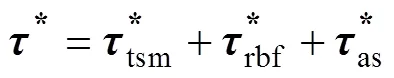

2.3 稳定性分析
在动力学中, ROV质量矩阵和科氏力矩阵满足以下关系

在对控制律的稳定性分析中, 为利用此关系, 选择李雅普诺夫函数为






由完全平方式可以得到







当存在推力饱和时, 将控制律代入ROV动力学方程中, 可得


同时, 由滑模面的定义式有
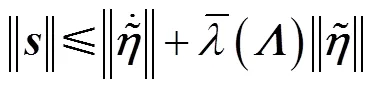

3 仿真验证
基于MATLAB Simulink可搭建图2所示仿真平台, 对抗饱和神经网络滑模控制进行验证。

图2 Simulink 系统仿真模型
ROV的主体属性如表1所示。为表示ROV各自由度间耦合作用的影响, 动力学方程模型使用的水动阻尼是基于文献[11]使用的2阶多项式模型, 相比于文献[8]中式(2)的简化阻尼力, 保留了更多的耦合项, 并考虑了不对称性影响。新型ROV的附加质量和水动力系数为文献[12]的计算流体力学(computational fluid dynamics, CFD)结果。在建模误差的设置中, 由于模型参数众多, 对控制的影响难以确定, 仿真中每个参数均设定一定的摄动量, 参数摄动通过标称值与真实值的相对误差表示。ROV的质量、惯性矩、浮心和重心容易测量, 在仿真计算中分别设置相对误差为10%, 15%, 10%和15%, 水动力系数误差设置为50%。仿真中, ROV运动模块采用CFD计算结果作为动力学模型求解的模型参数, 在控制系统模块中采用加入摄动量的标称模型参数计算控制力。
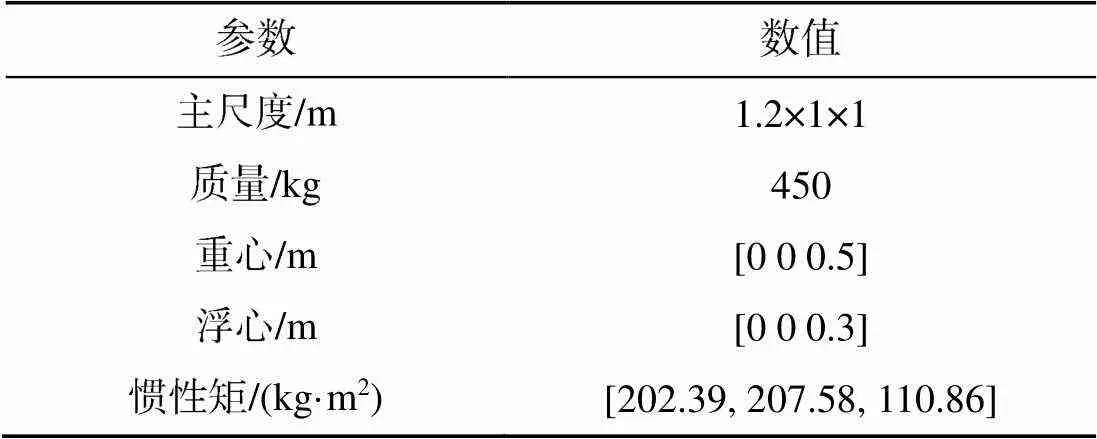
表1 ROV主要属性表
目标轨迹为使得ROV以0.1 m/s螺旋下潜, 旋转半径为5.8 m, 周期为85 s。同时要求艏向旋转速度为螺旋运动的角速度, 使得ROV前进速度与轨迹相切。加入抗饱和系统前后神经网络滑模控制的轨迹跟踪结果如图3~图6所示。
从图4可知, 在控制初期, ROV的位姿与目标位置存在5 m的偏差, 通过控制律计算输出的目标控制力极大, 因此长期处在推力饱和状态。如图5所示, 轨迹跟踪过程的前100 s中, 都存在剧烈的抖振。在推进器推力约束的影响下, 推力输出未达到理想状态, 使得各个自由度上的跟踪误差未能按照预期迅速减小, 推力输出持续处于饱和状态。即使通过反正切函数降低抖振, 依然伴有强烈的推力振荡现象。相比之下, 加入了抗饱和辅助系统后, ROV的横摇和艏摇姿态振荡得到削弱, 跟踪误差的收敛速度加快, 推进器推力饱和的持续时间降低, 跟踪误差减少。如图6所示, 无抗饱和系统时, 在600 s的轨迹跟踪过程中, RBF滑模控制的累计推力饱和时间为80.754 s, 加入抗饱和系统后, 同样的轨迹跟踪任务, 推进器累计推力饱和时间为39.663s。参考文献[13]对无模型滑模控制方法的判断指标, 通过均方差表示累计误差, 以此表示控制律的控制性能, 结果如表2所示。其中RBFSMC表示RBF神经网络滑模控制, AWRBFSMC表示抗饱和神经网络滑模控制器。相比于RBF神经网络滑模控制, 加入抗饱和系统后, ROV运动过程中在垂荡、横摇、艏摇方向出现的跟踪误差得到有效抑制, 同时, 其他运动方向上的跟踪性能也在一定程度上优于无抗饱和系统的控制律。

图3 螺旋下降过程位姿曲线
Fig.3Position and attitude curves during ROV spiral dive

图4 螺旋下降过程位姿误差曲线

图5 各螺旋桨推力输出曲线
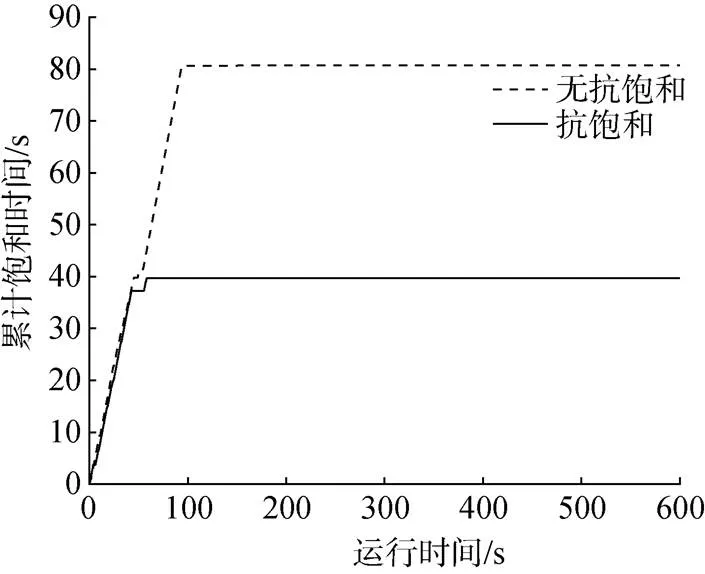
图6 累计推力饱和时间图

表2 2种控制方式位姿误差均方差对比
4 结束语
文中研究了海流干扰、未知建模误差和脐带缆扰动下的ROV轨迹跟踪问题。通过设计辅助系统, 利用反馈补偿实现抗饱和神经网络滑模控制, 解决了ROV控制初期神经网络学习未充分,跟踪误差偏大时的推力饱和问题, 实现了输入饱和情况下的轨迹跟踪控制。通过李雅普诺夫方法, 控制律的稳定性得到了严格证明。综合考虑了建模误差的耦合作用、海流干扰和脐带缆作用力等的影响, 对文中提出的轨迹跟踪控制进行了仿真研究。由仿真结果可知, 当ROV执行轨迹跟踪任务时, 抗饱和神经网络滑模控制器有效降低轨迹跟踪初期, 神经网络未完成学习时的推力饱和持续时间, 在一定程度上提高了跟踪性能。文中设计的抗饱和系统与Chen等[10]研究的类似, 仍需要饱和推力的有界性作为辅助系统稳定的前提条件, 如何提高抗饱和辅助系统的稳定性仍有待进一步的研究。
[1] 王啸. 基于自适应鲁棒算法的开架ROV悬停姿态控制研究[D]. 青岛: 中国海洋大学, 2014.
[2] Fernandes D D, Donha D C. Optimal Control System for a Semi-Autonomous Underwater Vehicle[J]. IFAC Proceedings Volumes, 2009, 42(18): 255-260.
[3] Fernandes D D, Sorensen A J, Pettersen K Y, et al. Output Feedback Motion Control System for Observation Class ROVs Based on a High-gain State Observer: Theoretical and Experimental Results[J]. Control Engineering Practice, 2015, 39: 90-102.
[4] 朱琦. 作业型水下机器人姿态控制方法研究[D]. 杭州: 浙江大学, 2018.
[5] Chu Z, Xiang X, Zhu D, et al. Adaptive Fuzzy Sliding Mode Diving Control for Autonomous Underwater Vehicle with Input Constraint[J]. International Journal of Fuzzy Systems, 2018, 20(5): 1460-1469.
[6] 刘金琨. RBF神经网络自适应控制Matlab 仿真[M]. 北京: 清华大学出版社, 2014: 57-60.
[7] 夏俊. 基于RBF神经网络的无人水面舰艇自适应控制[J]. 机械制造与自动化, 2019, 48(3): 185-188.
[8] Fossen T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. USA: John Wiley & Sons, Inc., 2011.
[9] Huo X, Ge T, Wang X, et al. Horizontal Path-following Control for Deep-sea Work-class ROVs Based on a Fuzzy Logic System[J]. Ships and Offshore Structures, 2018, 13(6): 637-648.
[10] Chen M, Ge S S, Ren B, et al. Adaptive Tracking Control of Uncertain MIMO Nonlinear Systems with Input Constraints[J]. Automatica, 2011, 47(3): 452-465.
[11] 徐诗婧. 开架式ROV水动力特性与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
[12] 薛乃耀, 王冬姣, 叶家玮, 等. 开架式水下机器人操纵性水动力系数计算[J]. 广东造船, 2020, 39(1): 25-28.
Xue Nai-yao, Wang Dong-jiao, Ye Jia-wei, et al. Maneuverability Coefficients Calculation of an Open-frame Underwater Remote Operated Vehicle[J]. Guangdong Shipbuilding, 2020, 39(1): 25-28.
[13] Salgado-Jimnez T, García-Valdovinos L G, Delgado- Ramírez G. Control of ROVs Using a Model-free 2nd- Order Sliding Mode Approach[EB/OL]. Sliding Mode Control. (2011-04-11)[2019-09-18]. https://www.intechopen. com/books/sliding-mode-control/control-of-rovs-using-a- model-free-2nd-order-sliding-mode-approach.
Anti-saturation Control Design for Remote Operated Vehicle Considering Model Error
XUE Nai-yao, LIU Kun, WANG Dong-jiao, YE Jia-wei
(School of Civil and Transportation Engineering, South China University of Technology, Guangzhou 510640, China)
To investigate the trajectory-tracking problems of a new open-frame remote operated vehicle(ROV), a new variable gain anti-saturation auxiliary system is proposed, which is based on the radial basis function neural network sliding mode control law and considers thrust constraints. The stability of the control law was proved using the Lyapunov stability theory. A simulation was built using MATLAB Simulink, and modeling errors, ocean current disturbances, and cable action force are considered during the trajectory-tracking study, which is similar to the actual working environment of a ROV. The results show that after incorporating the anti-saturation system, the thrust saturation duration of the propulsion system decreased by 27% during the ROV track tracking, the cumulative tracking error of each degree of freedom decreased, and the tracking error of the roll and heave degrees decreased significantly, demonstrating the reliability of the new control law.
remote-operated vehicle(ROV); thrust saturation; trajectory tracking; radial basis function neural network; sliding mode control
TJ630.32;TP183
A
2096-3920(2021)03-0272-06
10.11993/j.issn.2096-3920.2021.03.004
薛乃耀, 刘鲲, 王冬姣, 等. 考虑模型误差的ROV抗饱和控制设计[J]. 水下无人系统学报, 2021, 29(3): 272-277.
2019-12-09;
2020-06-29.
国家重点研发计划项目(2016YFC1400202); 广东省级科技计划项目(2015B010919006); 中央高校基本科研基金(D2192650).
薛乃耀(1994-), 男, 在读硕士, 主要研究方向为水下机器人控制.
(责任编辑: 许 妍)
