架空线缆高空电磁脉冲传导环境参数的计算与分析

刘 政，黑东炜，毛从光，聂 鑫，陈 伟，崔志同，杜传报

(西北核技术研究所，西安710024；强脉冲辐射环境模拟与效应国家重点实验室，西安710024)

高空电磁脉冲(high-altitude electromagnetic pulse, HEMP)作用范围广、电场强度大、频谱范围宽，可对数千千米的通信及电力基础设施造成严重威胁[1-4]。架空电力线缆由于架空高、线缆长，极易同高空电磁脉冲耦合，产生快上升沿、大幅值的电压及电流，导致局部放电、击穿或烧毁，对端口设备配电网变压器、绝缘子等构成威胁[5-6]。美国电磁脉冲委员会2008年发布的评估报告——《电磁脉冲袭击对国家关键基础设施的影响》指出，高空电磁脉冲对广域分布式电力系统具有严重威胁。国际电工委员会(IEC)根据大量不同方向入射的电磁脉冲场线耦合终端的耦合电流波形统计，针对长线端口制定了IEC 61000-2-10电磁脉冲传导环境标准[7-8]。然而，由于电力系统属于广域分布式系统，系统内的架空电力线缆往往横跨数千千米，因此，在不同区域中，线缆端接设备所处的地磁倾角与架空高度均可能发生变化，这些变化可能会对电磁脉冲传导环境产生影响。

本文基于Agrawal散射电压的传输线耦合模型，充分考虑了高空电磁脉冲源区与架空电力线缆之间相对位置的随机性，推导了架空电力线缆高空电磁脉冲传导环境变量参数计算公式，计算了不同地磁倾角及不同架空高度下的电力线缆传导环境波形参数，并与IEC 61000-2-10标准波形参数进行了对比分析，为电力系统高空电磁脉冲易损性评估提供参考。

1基于Agrawal散射电压的传输线耦合模型及有效长度的选取

损耗大地上，高空电磁脉冲传输的场线耦合计算模型，如图1所示。

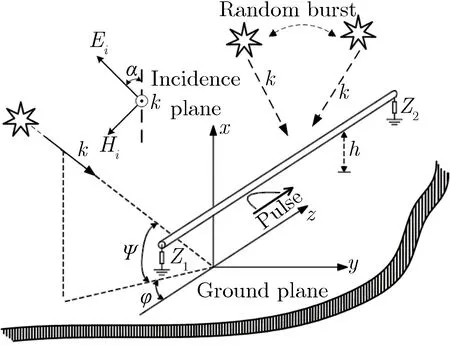
图1高空电磁脉冲传输的场线耦合计算模型Fig.1HEMP coupling model of transmission line

本文采用Agrawal散射电压的传输线耦合模型，将入射场同散射场分开计算，主要计算方程为

(1)

其中，Vs(x)为散射电压；V2′(x)为切向电压；Z′和Y′分别为传输线单位长度的阻抗和导纳。电流及传输线两端的电压可通过BLT方程求解得到。

(2)

其中，ρ1和ρ2分别为传输线两端的反射系数；S1和S2分别为传输线的两个激励源；l为架空电力线缆长度。对于架空电力线缆的高空电磁脉冲场线耦合响应，入射波通常选用IEC 61000-2-9中的双指数脉冲，电场强度波形可表示为

E(t)=kEmax(e-αt-e-βt)

(3)

其中，k=1.3；Emax=50 kV·m-1；α=4×107s-1；β=6×108s-1。

架空电力线缆的高空电磁脉冲场线耦合存在临界耦合长度，即当电力线缆长度达到某个固定值时，耦合电压或电流不再随电力线缆长度的增加而增加，耦合电流峰值Ip趋于饱和[9]。图2给出了掠入射时耦合电流峰值Ip与架空电力线缆长度l之间的关系。

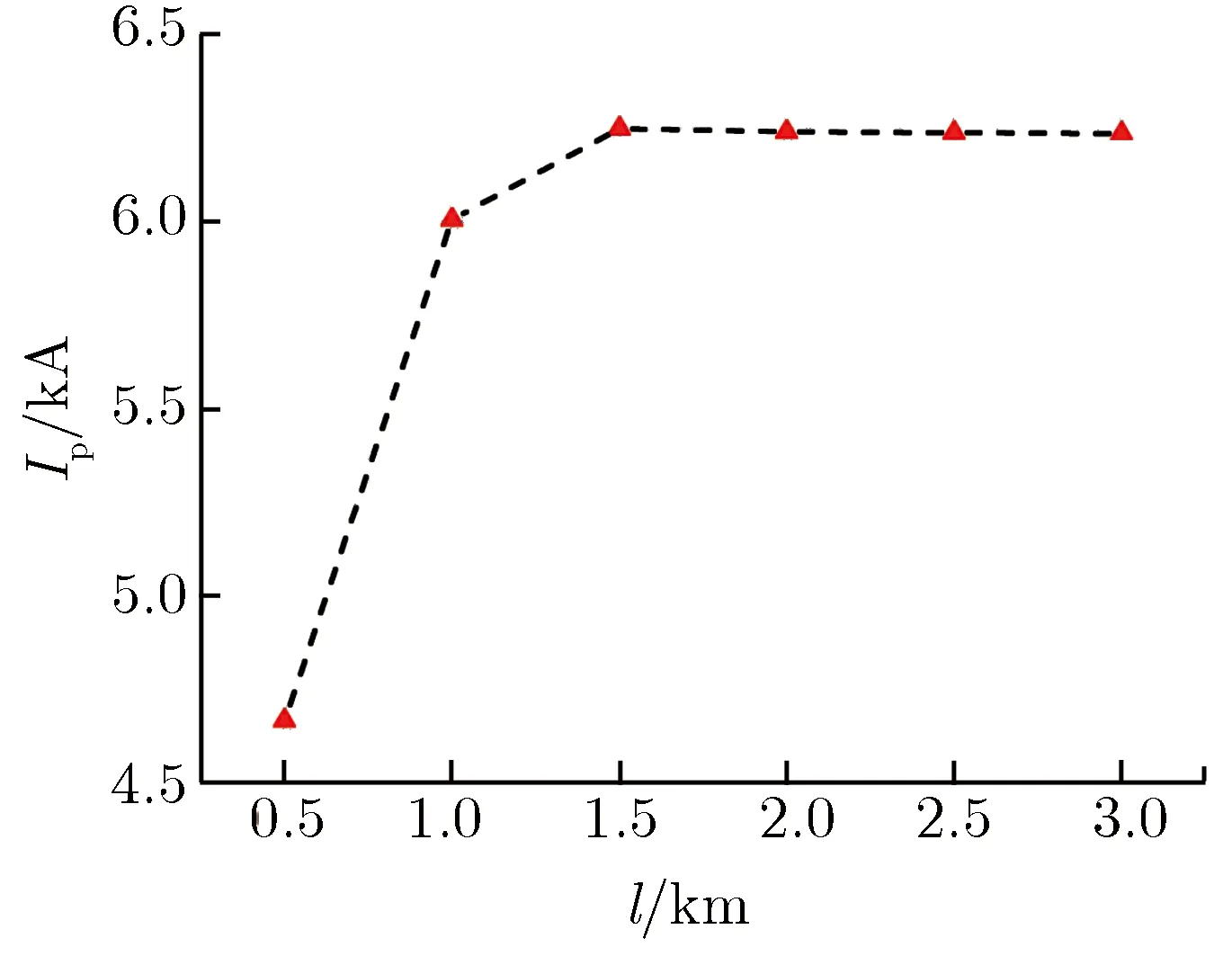
图2掠入射时耦合电流峰值与架空电力线缆长度之间的关系Fig.2Coupling peak current vs. elevated line lengthwith grazing incidence

由图2可见，当架空电力线缆长度超过1.5 km时，掠入射情况下的耦合电流峰值不再随架空电力线缆长度的变化而改变，因此本文后续计算分析时，为保证传导环境参数计算中架空线缆长度大于临界耦合长度，选取2 km作为架空电力线缆的标准长度。

2架空电力线缆高空电磁脉冲传导环境生成

架空电力线缆在高空电磁脉冲作用下产生的耦合电流峰值、上升沿最小值及脉冲宽度最大值一般不会集中在一种入射条件下出现。为了能够充分地考核被试品的性能，目前采用的传导环境波形是通过穷举大量入射方向和不同极化角度的场线耦合响应，并对计算的电流峰值及整流脉冲特征参数等进行统计分析，生成类似包络线性质的双指数波形。图3给出了归一化后的双指数脉冲波形。其中，η为上升沿系数，取值在[0,1]之间；脉冲上升沿tr为波形从η1=0.1上升到η2=0.9所用的时间；脉冲半宽tw为ηw=0.5处的波形宽度；传导环境生成过程中使用的有效脉宽tpw为ηpw=1/e处的波形宽度[8]。

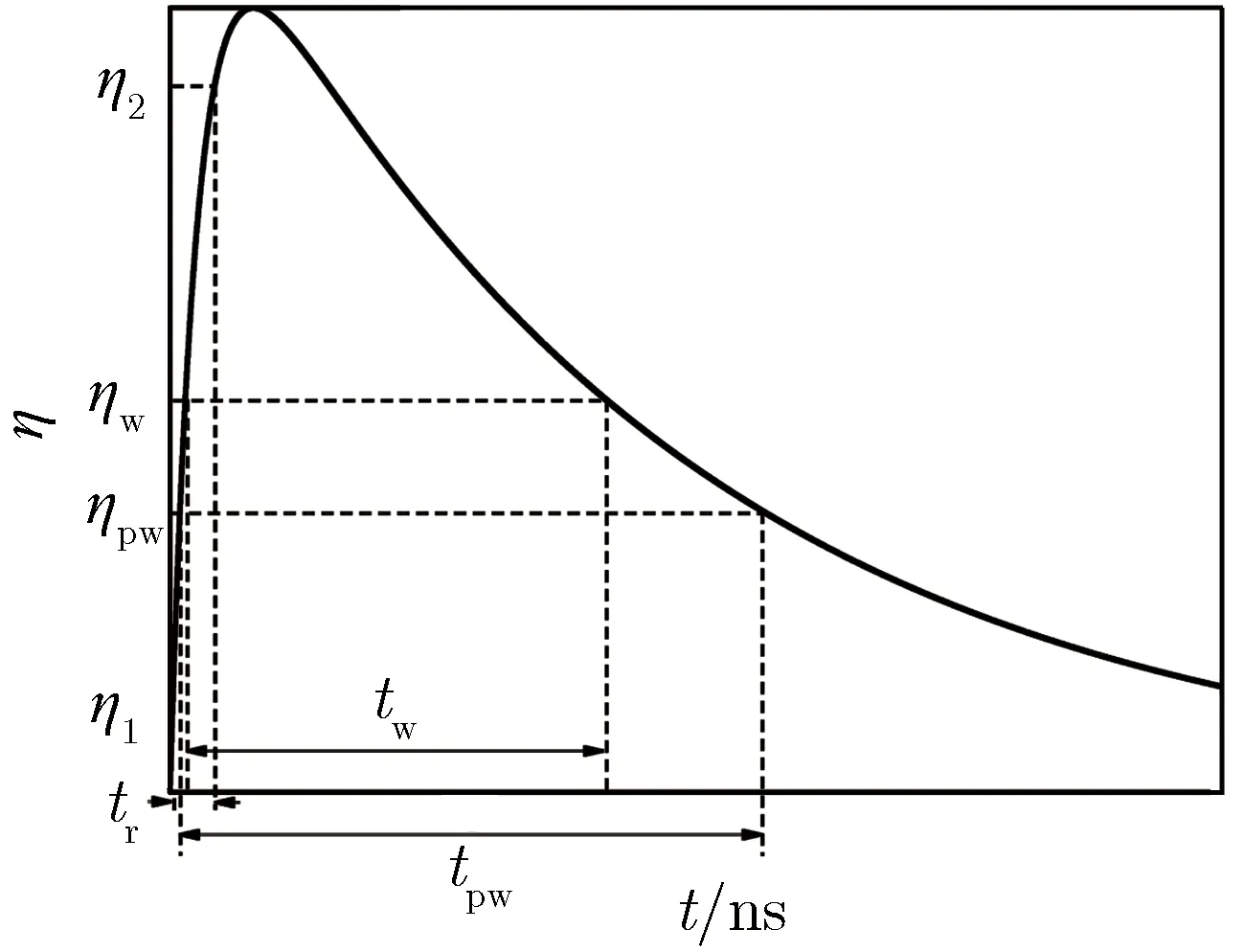
图3归一化后的双指数脉冲波形Fig.3Normalized double exponential pulse waveform

生成高空电磁脉冲传导环境的步骤为

1)确定架空电力线缆参数，如架空高度、长度等。通常，架空高度越高，耦合电流峰值越大；长度越长，耦合电流峰值越大，但存在耦合临界长度。

2)确定地磁倾角。地磁倾角会影响高空电磁脉冲的极化方向，从而影响最终的耦合响应。

3)确定电力系统所处的环境参数，如大地电导率、相对介电常数等。

4)针对给定参数的电力系统架空线缆，通过穷举所有架空线缆与高空电磁脉冲源区之间的位置关系，确定不同的方位角，得到大量样本的终端耦合电流波形。

5)提取耦合电流波形参数，确定耦合电流峰值和整流冲击值，并对参数进行统计排序，得到相应的累计概率分布曲线；在所有样本中找到耦合响应的最大电流变化率，作为后续传导环境计算的依据。

6)选取给定概率下的耦合电流峰值作为传导环境波形的峰值；将耦合电流峰值的80%除以最大电流变化率得到传导环境波形的上升沿；将给定概率下的整流冲击值除以耦合电流峰值得到相应的有效脉宽tpw，从而进一步计算得到脉宽半宽tw。

高空电磁脉冲传导环境生成过程中使用了耦合电流峰值、最大电流变化率和整流冲击值3个电磁范数概念。耦合电流峰值Ip是耦合电流在时域上的无穷范数，是所有耦合电流波形峰值绝对值中的最大值，表征电磁脉冲的威胁等级，可表示为

Ip=|I(t)|max

(4)

最大电流变化率ε是耦合电流在时域上的无穷范数，是所有耦合电流波形中变化率绝对值中的最大值，表征电磁脉冲上升沿变化的快慢，常出现在掠入射的情况下，可表示为[8]

(5)

整流冲击值Q是耦合电流在时域上的1-范数，是电流幅值的绝对值在全时域上的积分，是与能量有关的参数，可表示为

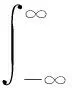
(6)

由高空电磁脉冲传导环境生成步骤可知，耦合模型中线缆参数、地理参数及环境参数的变化均会使最终的高空电磁脉冲传导环境参数发生变化，因此，应针对电力系统的不同节点，分别计算各处设备的高空电磁脉冲传导环境。

3场线耦合模型中的物理参数及其分布特性

高空电磁脉冲场线耦合模型中相关物理参数的统计分布特性决定了场线耦合情况的穷举结果。由于广域分布式电力及通信系统节点设备的地理位置通常是固定的，因此，本文从设备角度出发，充分考虑高空电磁脉冲源区与设备之间相对位置的随机性，建立场线耦合模型。该模型中的主要参数为

1)源区高度H

源区高度H表示高空电磁脉冲初始发生区域距地球表面的垂直距离。在没有特殊指定的情况下，认为源区高度在[50 km, 400 km]之间服从均匀分布。

2)地心角β

地心角β的定义，如图4所示。β表示源区和设备分别与地心连线之间的夹角。通常认为，地心角β在[0,βmax]之间服从均匀分布，最大值βmax由源区高度决定，可表示为

(7)

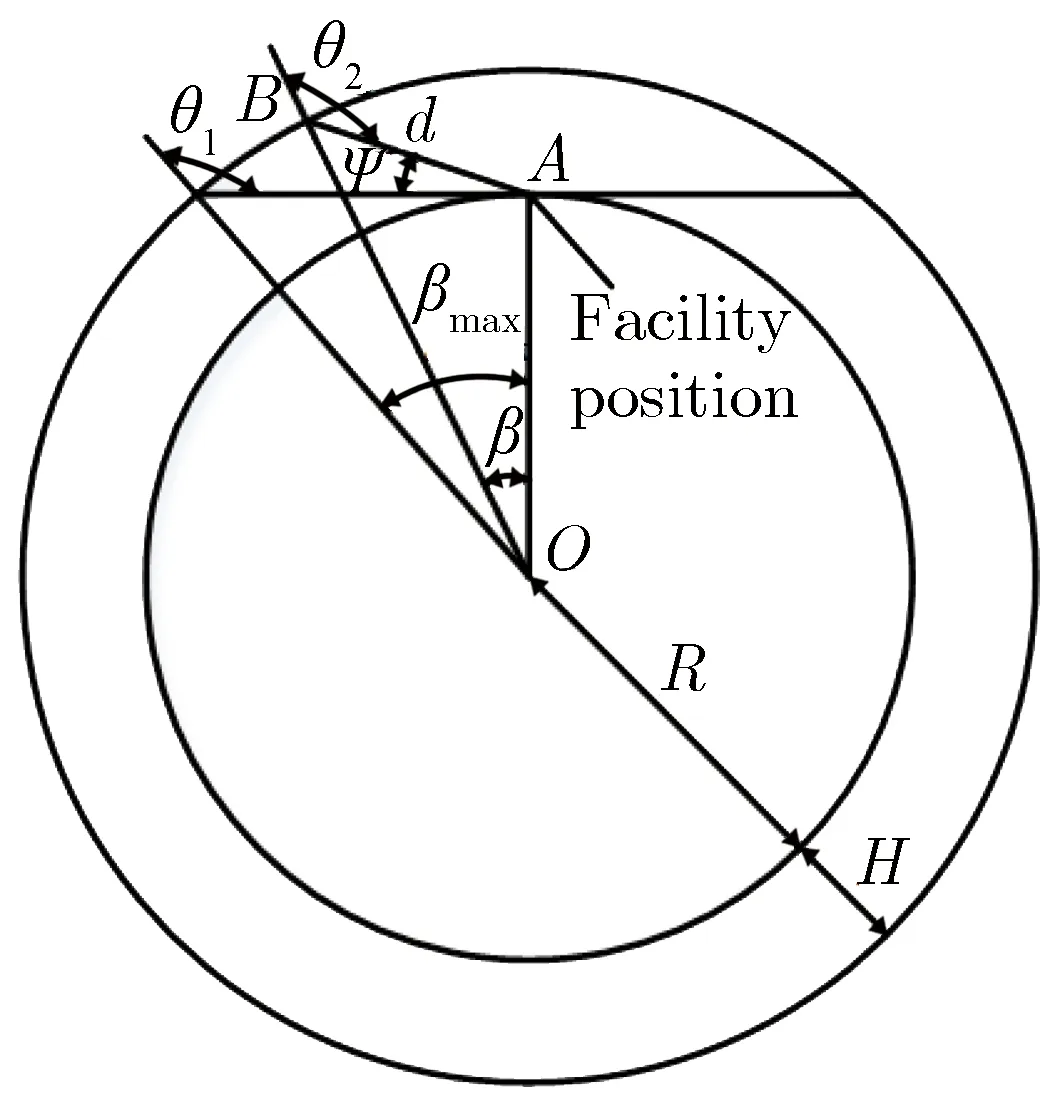
图4地心角β的定义Fig.4Definition of core angle β

3)方位角δ

高空电磁脉冲源区与架空线缆的3维空间位置关系，如图5所示。图5中，方位角δ表示线缆设备处(observer)与源区投影处地磁南极的位置关系，通常认为，δ在[0,2π]之间服从均匀分布。

图5高空电磁脉冲源区与架空线缆的3维空间位置关系Fig.5Three-demensional relationship betweenburst and elevated line

4)方向角φ

上述4个独立变量的分布特性使高空电磁脉冲的场线耦合响应具有随机性。图4及图5中变量之间的相互关系为

(8)

(9)

其中，d表示高空电磁脉冲源区与架空线缆设备之间的直线距离，可表示为

(10)

5)地磁倾角θb

地磁倾角θb表示地球表面任一点总地磁场强度的矢量方向与xOy水平面的夹角。通常，北半球的地磁倾角为正，南半球的地磁倾角为负。电磁脉冲自源区传播至线缆设备处时，极化方向角α的分布特性会受到θb的影响。α可表示为

(11)

4统计特性分析方法及数值验证

高空电磁脉冲传导环境的计算与分析中，常用蒙特卡罗方法。但当开展不同地理位置、架空高度及大地电导率等多种因素对高空电磁脉冲传导环境的影响分析时，需要多次使用蒙特卡罗方法，计算效率较低，因此，亟需一种高效的统计特性分析方法。

多项式混沌展开(polynomial chaos，PC)方法源自Wiener提出的同性混沌法，是一种数理基础严密的统计特性分析方法。该方法利用展开正交多项式的性质，将随机过程的随机特性转移到多项式的系数上，建立随机变量与随机响应量之间的函数关系，可求解随机响应量的全部概率信息。对于具有多变量的传输线场线耦合模型，该方法可表示为

Iload=Y(ξ)

(12)

其中，ξ=(ξ1,ξ2,ξ3，…，ξn)T为n维随机变量向量。根据随机变量所对应的多项式，场线耦合模型可展开为

(13)

对式(13)进行截断可得

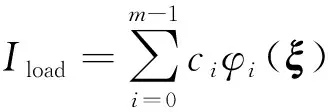
(14)

截断后的项数m由变量数n及多项式最高阶数p决定，可表示为

(15)

根据多项式展开的正交性，多项式的系数可通过各基项对随机过程在Hilbert空间内作内积得到，计算公式为

(16)

通过多项式系数及相关内积，可计算得到场线耦合模型的统计特性参数。均值和方差的计算公式分别为

Iload-mean=E(Y(ξ))=a0

(17)

(18)

高空电磁脉冲场线耦合模型中，变量H，β，δ，φ均服从均匀分布，与这些变量对应的正交多项式为勒让德正交多项式。

为了验证多项式混沌展开方法的高效性与准确性，本文计算了包含H，β，δ，φ这4个变量的高空电磁脉冲场线耦合统计特性参数，得到耦合电流均值Iload-mean及其标准偏差σ随时间的变化关系，如图6所示。为方便比较，图6还给出了蒙特卡罗方法(MC)的计算结果。计算中，蒙特卡罗方法的样本量为246 240，多项式混沌展开方法的高斯积分采样点为10。

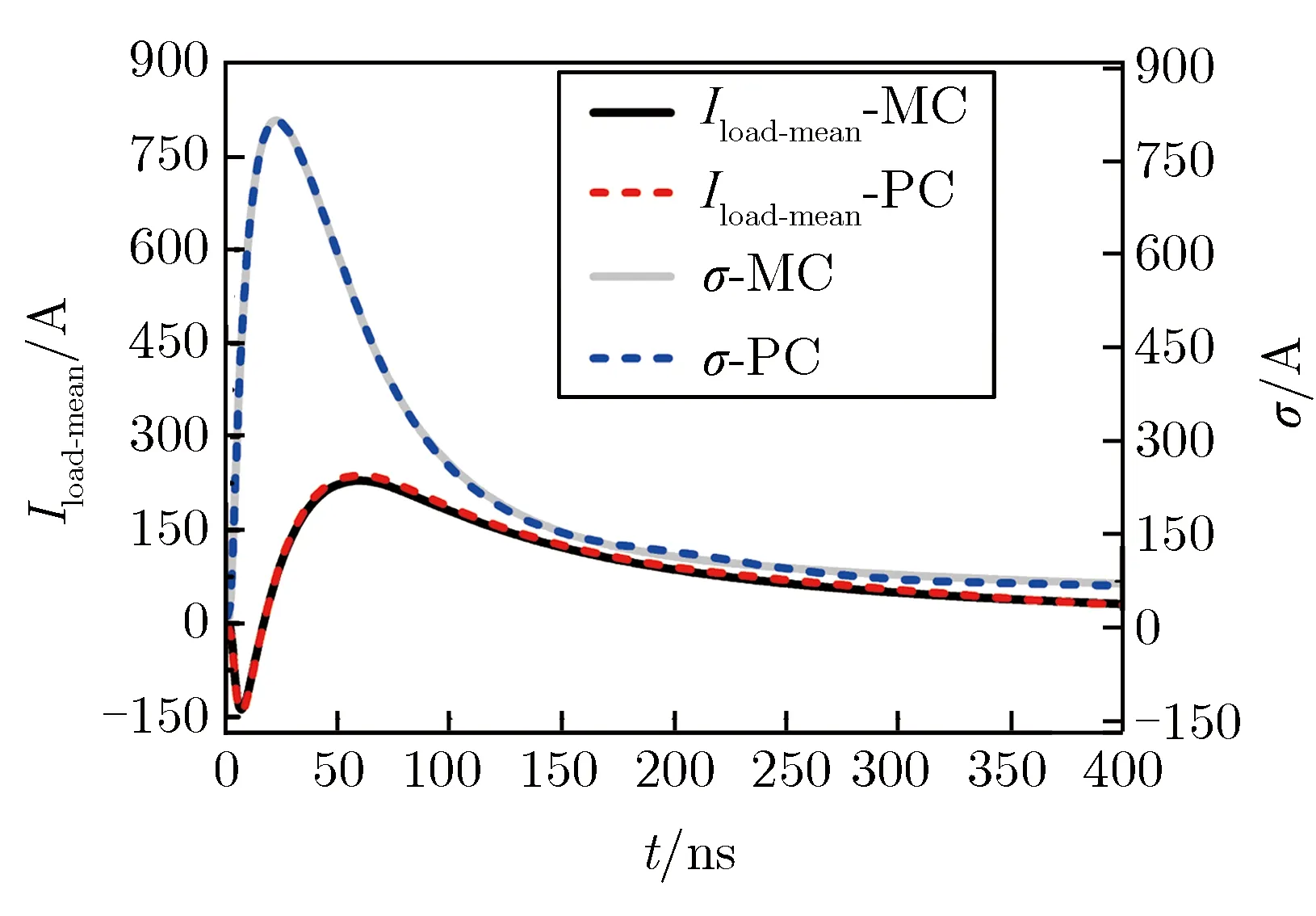
图6耦合电流均值及其标准偏差随时间的变化关系Fig.6Mean value and its standard deviationof coupling current vs. time

由图6可见，多项式混沌展开方法得到的耦合电流均值及其标准偏差与蒙特卡罗方法的计算结果相符，但蒙特卡罗方法的计算用时为25.81 h，多项式混沌展开方法的计算用时为0.63 h，前者是后者的41倍。这表明多项式混沌展开方法中，高斯积分的计算精度满足多项式混沌展开的要求，多项式展开所选取的阶数p也满足需求，且多项式混沌展开方法在传导环境计算中具有高效性。

5高空电磁脉冲传导环境数值计算与分析

利用多项式混沌展开方法的解析表达式，可以快速地得到大量波形，从而得到相关参数的统计特性分布。选取地磁倾角θb为45°，线缆长度l为2 km，架空高度h为10 m，大地电导率γg为0.01 S·m-1，计算得到耦合响应特征参数的统计特性分布，如图7所示。由图7可见，由解析多项式得到的累计概率P与蒙特卡罗方法得到的结果吻合良好，不同概率下的参数取值，如表1所列。

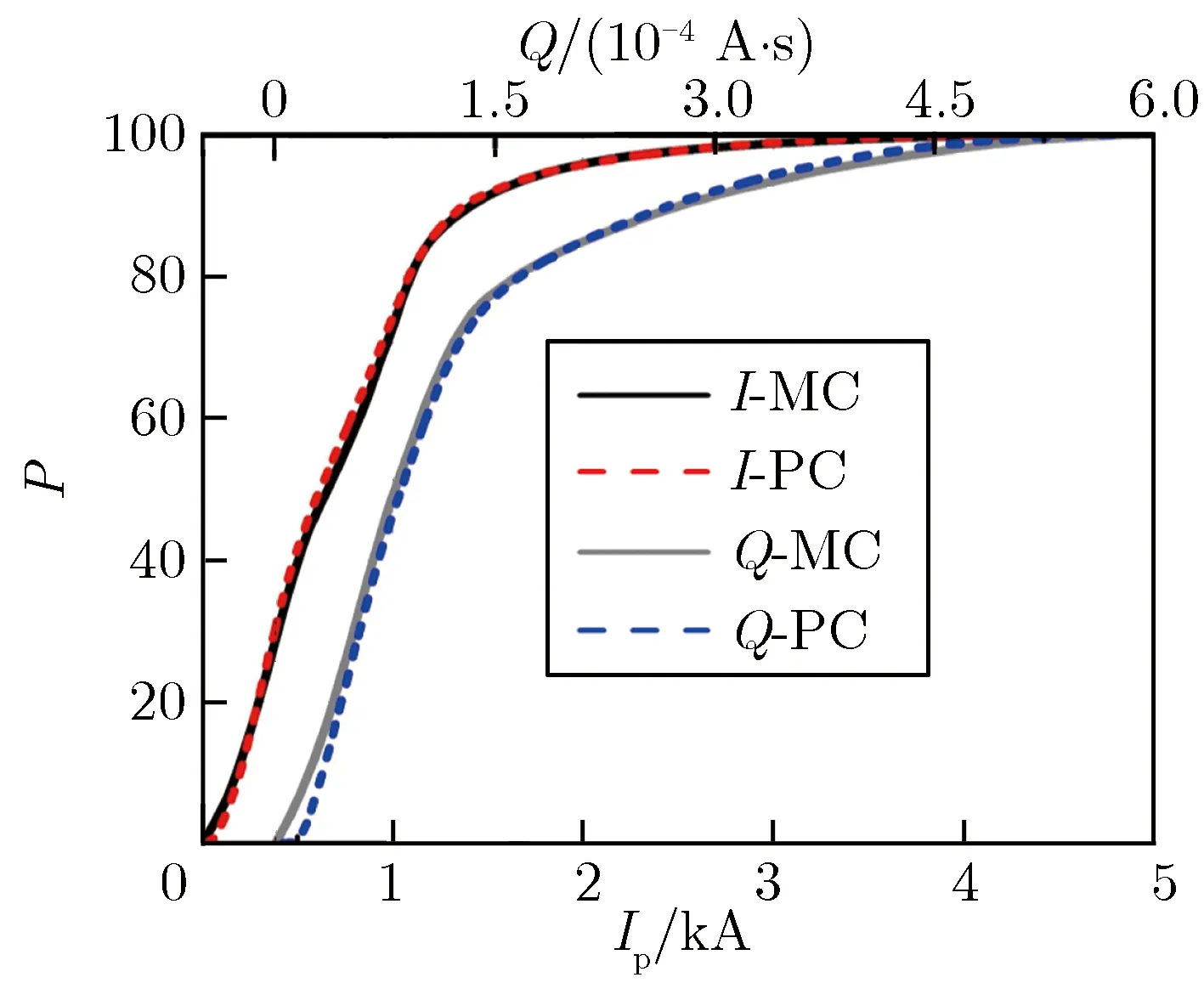
图7耦合响应特征参数的统计特性分布Fig.7Probability distribution function of specificparameters in coupling response

表1不同概率下的参数取值Tab.1Norms with different confidence

本文在掠入射条件下的耦合电流中得到电流最大变化率为4.62×1011A·s-1，有效脉宽tpw取各概率中对应的最大值195.85 ns，电流峰值分别取概率为99%和99.9%时的相应值，按照第2节中步骤进行双指数波形拟合，得到θb=45°时，线缆长度l为2 km，架空高度h为10 m，大地电导率γg为0.01 S·m-1条件下的高空电磁脉冲传导环境波形，如图8所示。为方便比较，图8还给出了IEC 61000-2-10标准波形。图8中传导环境波形参数的对比，如表2所列。由图8和表2可见，对于固定地理位置的架空电力线缆端接设备，当采用高概率时，计算所得的传导环境波形较标准电流峰值更高、上升沿更快、脉冲半宽更大。

图8高空电磁脉冲传导环境波形Fig.8The conducted environment waveform of HEMP

表2传导环境波形参数的对比(θb=45°)Tab.2Comparison of conducted environment parameters

图9给出了不同架空高度下，架空电力线缆传导环境波形耦合电流峰值Ip(P=99.9%)随地磁倾角θb的变化关系。由图9可见，Ip的取值波动范围为2～6 kA；在θb固定时，Ip随h的增大而逐渐增大；在h固定时，Ip随θb的增大而逐渐减小。

图9不同架空高度下，耦合电流峰值(P=99.9%)随地磁倾角的变化Fig.9Coupling current peak (P=99.9%) vs. dip angle at different heights

分析认为，传输线终端垂直段电场积分的变大会导致终端耦合电流变大，因此，在给定概率下，传导环境波形的耦合电流峰值随架空高度的增大而增大。地磁倾角的增大会使极化角α的分布向水平极化集中，图10给出了不同地磁倾角下的极化角累计概率分布。

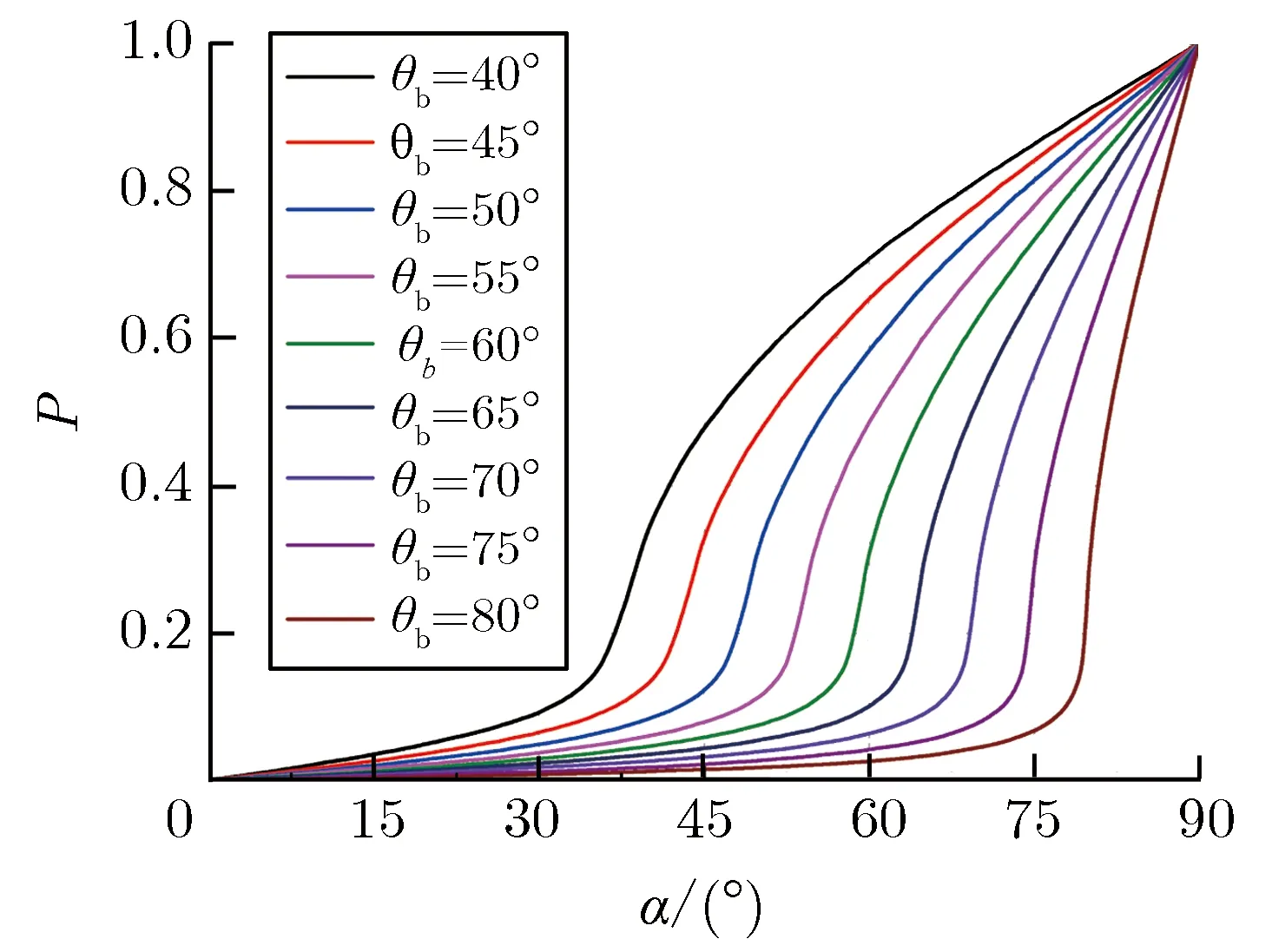
图10不同地磁倾角下的极化角累计概率分布Fig.10Probability distribution function of polarizationangle at different dip angles

对于架空长线缆，由于其耦合电流峰值常出现在掠入射的情况下，即完全垂直极化方式下的电磁脉冲对架空长线的耦合是最大的，因此，在极化角α更趋向于水平极化分布的高地磁倾角处，场线耦合更多的情况是偏水平极化，导致低幅值的终端耦合电流占居主要部分，所以，在给定概率下，传导环境波形的耦合电流峰值随地磁倾角的增大而逐渐减小。

图11给出了不同架空高度下，架空电力线缆传导环境波形上升沿tr(P=99.9%)随地磁倾角θb的变化关系。

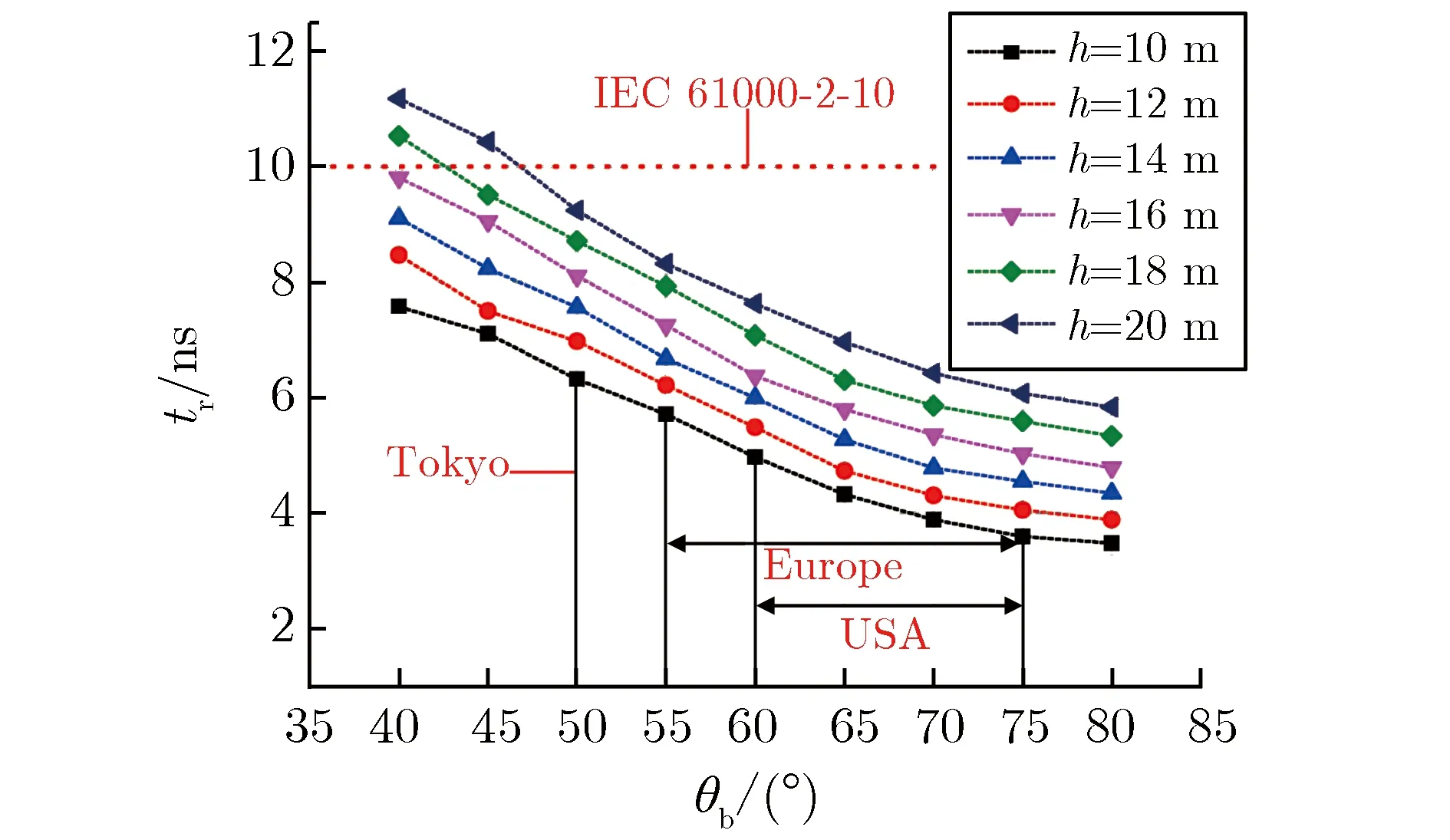
图11不同架空高度下，上升沿(P=99.9%)随地磁倾角的变化关系Fig.11 Risetime (P=99.9%) vs. dip angleat different heights

由图11可见，tr取值的波动范围为4～12 ns；在θb固定时，tr随h的增大而逐渐增大；在h固定时，tr随θb的增大而逐渐减小。这是因为tr是由架空线缆终端耦合电流峰值的80%除以最大电流变化率峰值得到的，而最大电流变化率峰值在线缆参数固定时不会发生改变。最大电流变化率峰值随线缆架空高度的变化关系，如图12所示。

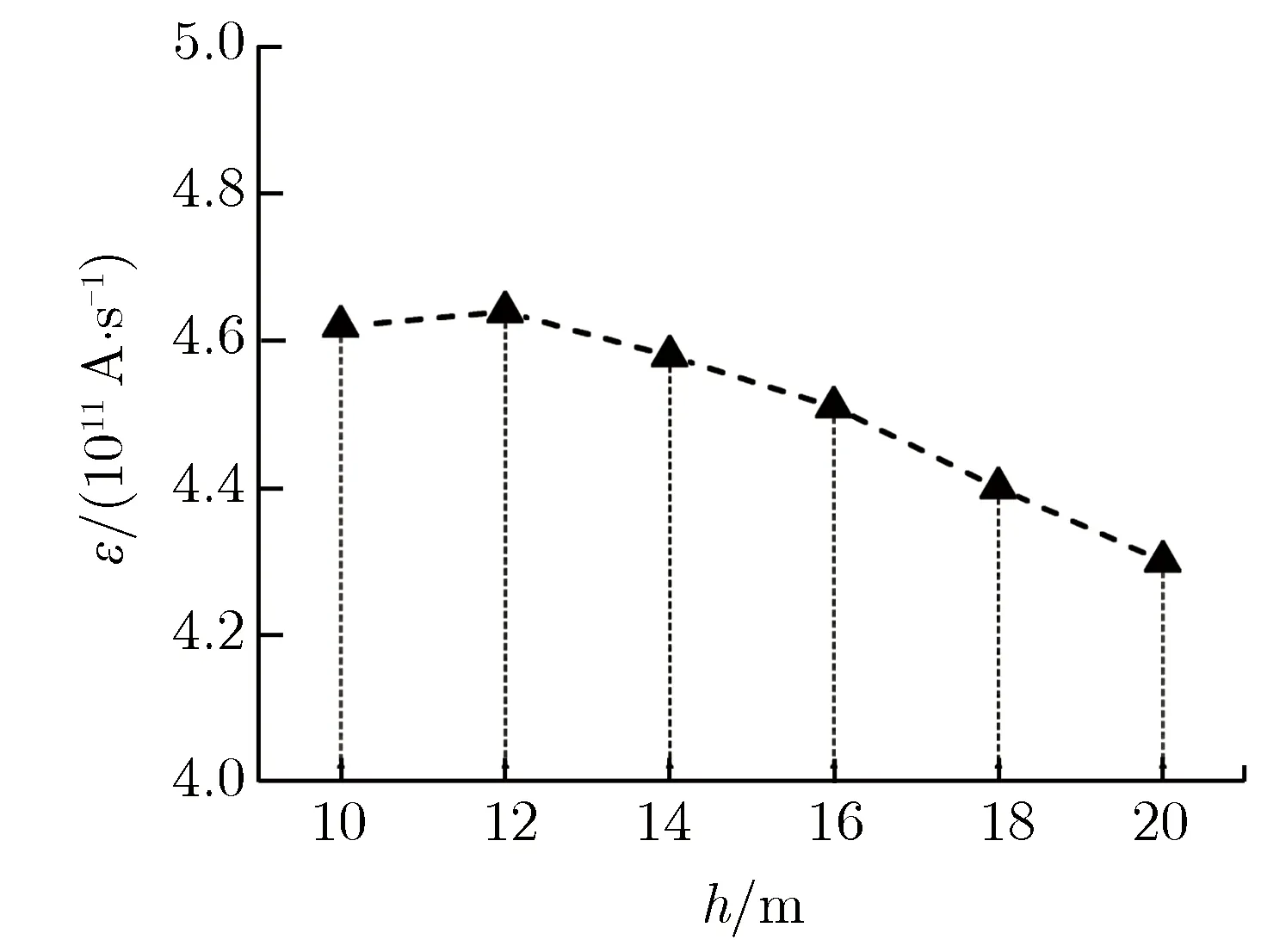
图12最大电流变化率峰值随线缆架空高度的变化关系Fig.12Max derivative value of current vs. height

由图12可见，最大电流变化率峰值随线缆架空高度的增加仅发生微小降低。因此，图11中上升沿随线缆架空高度及地磁倾角的变化趋势与图9中耦合电流峰值的相应变化趋势基本一致。

图13给出了不同架空高度下，架空电力线缆传导环境波形脉冲半宽tw(P=99.9%)随磁倾角θb的变化关系。由图13可见，tw的取值范围为70～150 ns；在θb固定时，tw随h的增大而逐渐减小；在h固定时，tw随θb的增大而逐渐减小。

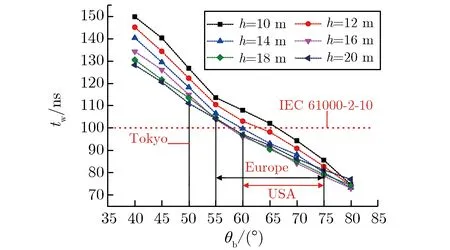
图13不同架空高度下，脉冲半宽(P=99.9%)随地磁倾角的变化关系Fig.13Pulse half width(P=99.9%) vs. dipangle at different height

典型的电力系统架空线路配电网工程设计中，水泥单杆或钢管杆高度通常为10～20 m，且分布广泛，各节点设备处的地磁倾角变化较大。地磁倾角在欧洲的变化范围为55°～75°，在美国为60°～75°，在加拿大北部可达90°，因此，在高空电磁脉冲性能考核时应当使用不同的传导环境试验波形。如果使用IEC 61000-2-10中给出的单一传导环境波形，则对地磁倾角较小区域的设备，可能出现电流峰值较低的欠考核情况；反之，对地磁倾角较大区域的设备，则可能出现电流峰值较高的过考核情况。

6结论

本文将多项式混沌展开方法与基于Agrawal散射电压的传输线模型相结合，提出了架空电力线缆高空电磁脉冲传导环境的生成方法和步骤，验证了方法的可行性，提高了计算效率。计算结果表明，不同地理位置处及不同架空高度下，电力系统线缆终端设备所受的高空电磁脉冲传导环境不尽相同，脉冲电流峰值的变化范围为2～6 kA，脉冲上升沿的变化范围为4～12 ns，脉冲半宽的变化范围为70～150 ns。建议在性能考核试验中，应针对具体问题进行具体分析，以免出现设备性能欠考核或过考核的情况。