《信号与系统》课程的MATLAB仿真——从一道例题展开

陈昌兆

（安徽理工大学 力学与光电物理学院，安徽 淮南232001）

0 引 言

《信号与系统》是电子信息类专业一门重要的专业基础课，是进一步学习后续课程如《数字信号处理》《通讯原理》《自动控制原理》等课程的基础.它是信息与通讯工程、电子科学与技术、控制科学与工程等国家一级学科在大学本科阶段的专业必修课.主要任务是研究信号与系统理论的基本概念和基本分析方法，通过建立信号与系统的数学模型并求解，然后对所得结果给以物理解释并开展相应的工程应用.由于课程的学习需要熟练使用多种数学工具、深刻理解其中蕴含的物理概念和原理并用来解决实际的工程问题，这些都给课程的教学造成了一定的困难.

如何积极有效地开展《信号与系统》的课程教学是摆在教师面前的十分突出的问题.由于传统的教学方式形式单一、内容乏味，很难在数学理论、物理概念和工程应用之间建立紧密的关联，这是导致学生难学、教师难教的主要原因.为了克服传统教学中存在的种种弊端，激发学生的学习积极性和主动性，国内外很多高校将互联网、多媒体、手机APP以及仿真等基于计算机的人机互动式教学手段引入到《信号与系统》课程教学中并起得不错的教学效果[1-5].例如，美国德克萨斯大学埃尔帕索分校已经连续多个学期将信息技术手段引入到课程教学中.参加该课程的学生可以通过Connexions、四基系统、交互式模拟和Openstax Tutor四种技术参与学习，利用Connexions模块可以在任意的时间和地点开展学习，并借助四基系统通过作业反馈等手段加深对课程中的重要专题的认识深度[4].阿根廷Rosario大学以J.C.Gomez[5]教授为首的《信号与系统》教学团队将网上演示和测试、多媒体课件、虚拟实验室等多种ICT（Information and Communications Technologies）工具引入到传统的课堂教学中，多年实践的结果表明传统教学和这些ICT工具的综合使用大大改善了课堂教学效果，提高了学生对课程学习的满意度，同时也提高了他们的学习成绩.

在多种多样的基于ICT的辅助教学中，计算机仿真最为行之有效，特别是MATLAB的出现给《信号与系统》课程的计算机辅助教学带来了便捷，其强大的数学计算功能、丰富的工具箱函数和可视化的图形用户界面给课程教学带来了极大的感官刺激，增强了课堂互动性，提高了学生学习的主动性和参与度.《信号与系统》课程的MATLAB仿真国内外有不少教材和参考书，如清华大学谷源涛教授[6]主编的《信号与系统—MATLAB综合实验》以及韩国中央大学W.Y.Yang等人[7]编写的《Signals and Systems with MATLAB 》，这些参考书系统、全面，但对初学者而言需要时间去练习并消化和吸收.实际上，对于初学者而言，快速入门至关重要，《信号与系统》虽然内容众多但贯穿其中的始终是一些重要的概念和分析方法，如卷积、单位冲激响应、傅里叶变换与频谱、拉普拉斯（z）变换与系统函数、滤波、调制和解调、根轨迹等等.在有限的教学时限下，教师选择能够涵盖多个关键知识点的经典例题进行MATLAB仿真不仅能加深学生对多个概念之间关联性的理解，还能取得事半功倍的教学效果.此处我们借助一个带通滤波系统典型例题的MATLAB分析阐述仿真软件在课程教学中的应用，虽然无法做到面面俱到，但至少是抓住了问题的关键.为了方便初学者，不仅附上每一个仿真的MATLAB程序，同时还有详细的中文注解，相信这些注解对初学者是大有裨益的.

1 带通滤波系统的MATLAB仿真

清华大学郑君里教授主编的教材《信号与系统》（第三版，高等教育出版社）的上册第301页有一道关于调幅信号作用于带通系统的例题，题干如下（略作改动）：

上述例题中激励信号是一种典型的调幅信号，cos(100t)为高频载波，1+cost为低频基带信号，调幅信号就是用低频调制信号去控制高频振荡的振幅，使高频振荡的振幅按照调制信号的规律振荡，这种调制技术在无线电波的有效发射等涉及频谱搬移的实际问题中都有应用.针对上述例题的MATLAB仿真至少可以包含以下内容：(1)激励信号的频谱观察；(2)系统函数分析系统；(3)输出响应；(4)在上述电路基础上引入反馈，进而进行根轨迹分析.这些重要专题的MATLAB仿真将分开阐述.

1.1 激励信号的频谱

频谱是《信号与系统》课程中极为重要的概念，时域信号与频谱之间通过傅里叶变换联系.频谱分析的目的是把复杂的时间历程波形，经过傅里叶分析分解为诸多谐波分量来研究，以获取动态信号中的各个频率成分幅度和相位分布，从而得到主要幅度和能量分布的频率值，完成对信号信息的定量解释.激励信号可以写成x(t)=cos(100t)+0.5cos(101t)+0.5cos(9t)，基于MATLAB程序的时域波形及其频谱图如下：

%% 信号波形

figure(1)

subplot(1,2,1)% 将图1定义为1×2矩阵图，

下一个图位于位置（1,1）

t=0:0.01:12; % 定义时间矢量t,抽样间隔为

0.01s

x=cos(100*t)+0.5*cos(101*t)+0.5*cos(99*t);% 定义 x矢量

N=length(x); % 求x矢量中元素个数N

plot(t,x)% 画信号波形图

xlabel('time in sec');

ylabel('x(t)');

title('Signal Waveform');

grid;

%% 信号频谱

subplot (1,2,2); % 下一个图位于位置（1,2）

x_f=fft(x); % 对信号x实行快速傅里叶变换

l=0:N-1; % 时间序列

k=(100/N)*l; % 频率序列

stem(k,abs(x_f))% 绘制幅度谱图

xlabel('frequency in Hz')

title('Spectrum of Signal');

grid;

从图1可以看出输入信号的包络线按照1+cost变化，变化周期为2π，最大振幅为2，对应的位置点为2nπ处.频谱图中采样频率fs=100Hz，奈奎斯特频率为fs/2=50Hz，谱图对奈奎斯特频率呈现对称性，频谱的峰值在16Hz左右，对应于原信号中角频率为100ras/s（线频率15.9Hz）成分，另外两种频率成分对应的角频率分别为99、101rad/s，幅度只有100ras/s处频率的一半，由于三种频率成分十分靠近，所以频谱叠在一起很难分辨.

图1 信号时域波形及其频谱

1.2 基于系统函数的分析

用系统函数分析系统是《信号与系统》课程中最常见的任务之一，因为系统函数刻画的是系统本身的性质，跟外加输入信号没有关系.系统函数实际上是单位冲激响应的拉普拉斯变换（z变换），而频响函数对应单位冲激响应的傅里叶变换.利用系统函数零极点分布可以分析系统的多种性质，如稳定性、因果性等等，而频响函数可以用来分析信号作用于系统时不同频率成分的幅度衰减和相移情况，是系统设计（如滤波器设计）的重要依据.针对当前的带通滤波系统用Matlab绘制该系统的零极点图、频响曲线和单位冲激响应.程序代码和图形如下：

%% 定义变量

t=linspace (0,5,401); % 定义时间矢量t，0~5s

之间共401个线性等分点

w=logspace (1,3,401); % 定义频率向量w,

10~103rad/s之间401个对数间隔点

num=[2 0]; % 定义系统函数分子多项式

den=[1 2 10001]; % 定义系统函数分母多项式

[poles,zeros]=pzmap (num,den); % 定义系统

函数零、极点向量

[mag,angle]=bode (num,den,w); % mag 和

angle定义为w处频响的幅度和相位

[y,x]=impulse (num,den,t); % y定义为t处系

统函数的冲激响应

%% 零极点图

figure(1)% 图1

subplot(2,2,1)% 将图1定义为2×2矩阵图，

下一个图位于位置（1,1）

plot(real(poles),imag(poles),'x',real(zeros),

imag(zeros),'o'); % 绘制零极点图

title ('Pole-Zero Diagram'); % 添加标题

xlabel ('Real'); % 添加 x轴标签

ylabel ('Imaginary'); % 添加 y轴标签

axis([-1.1 0.1 -120 120]); % 定义 x、y 轴范围

grid;

%% 频响曲线

subplot(2,2,2); % 下一个图位于位置（1,2）

semilogx(w,20*log10(mag)); % 绘制对数w值

幅度，以分贝为单位

title ('Magnitude of Bode Diagram'); % 添加标题

ylabel('Magnitude (dB)'); % 添加y轴标签

xlabel('Radian Frequency (rad/s)'); % 添加x轴

标签

axis([10 1000 -60 0]); % 定义 x、y 轴范围

grid;

subplot(2,2,4); % 下一个图位于位置（2,2）

semilogx(w,angle); % 绘制对数w值相位

title('Angle of Bode Diagram'); % 添加标题

ylabel('Angle (deg)'); % 添加y轴标签

xlabel('Radian Frequency (rad/s)'); % 添加x轴

标签

axis([10 1000 -90 90]); % 定义 x、y 轴范围

grid;

%% 单位冲激响应

subplot (2,2,3); % 下一个图位于位置（2,1）

plot(t,y); % 线性绘制阶跃响应

title ('Impulse Response'); % 添加标题

xlabel ('Time (s)'); % 添加x轴标签

ylabel ('Amplitude'); % 添加 y轴标签grid;

图2(a)显示H(s)的零点在0，极点在-1±j100，二者都是单阶的.单位冲激响应（图2(b)）是振荡衰减的，这与H(s)的反拉普拉斯变换表达式相吻合，即

图2(c)和(d)分别显示系统的幅频和相频特性，幅频曲线的基本特征是峰值点100rad/s，偏离此值，幅度迅速衰减.通带集中在100rad/s附近极小的频率范围（99~101rad/s），在此段频率范围，相位呈现线性特征.系统具有明显的带通滤波特性，通带的范围很窄，有效带宽大约2rad/s.

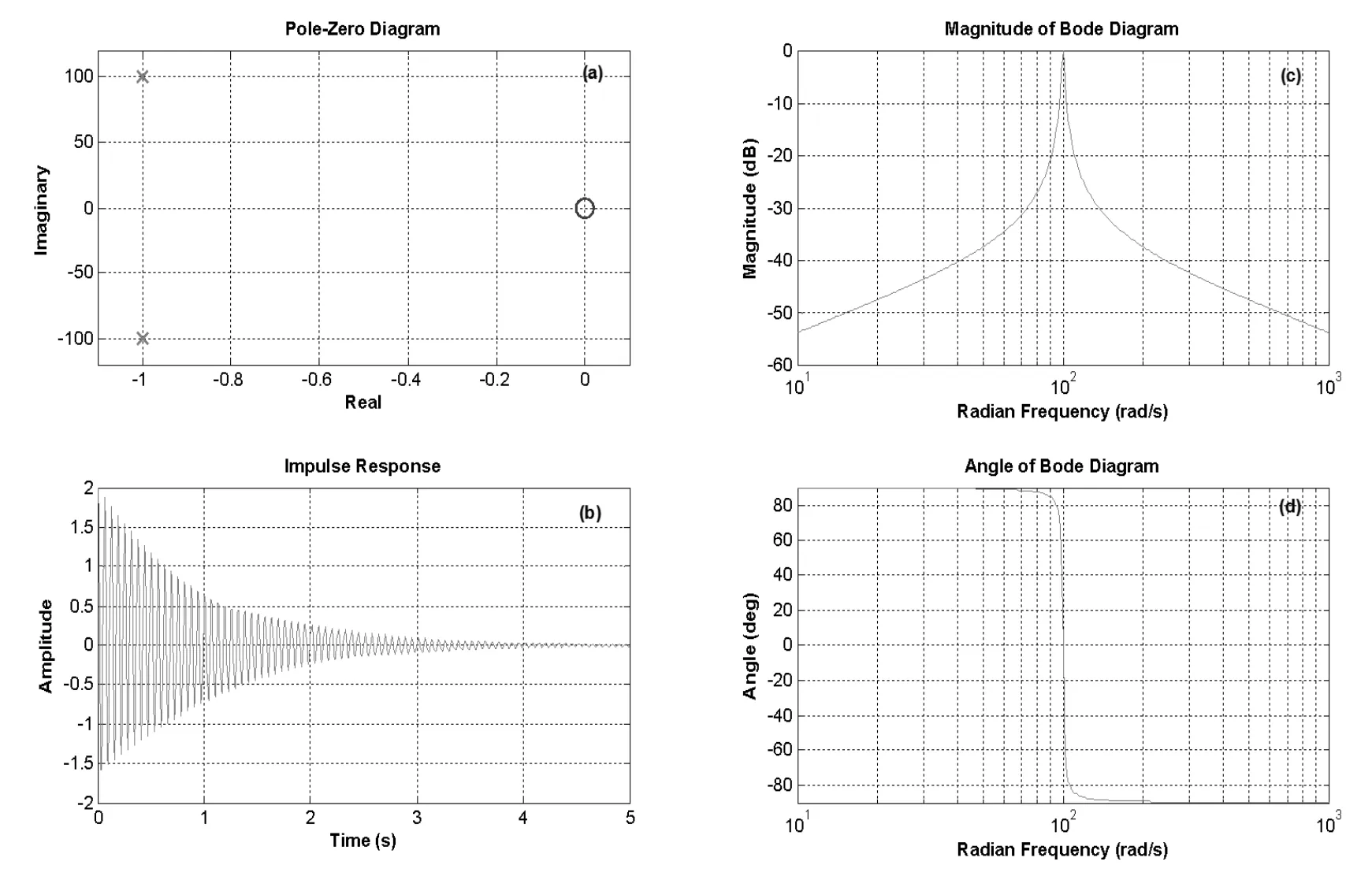
图2 (a)系统零极点分布; (b)单位冲激响应；(c)幅频特性曲线；(d)相频特性曲线

1.3 输出响应和频谱

利用lsim命令计算输出响应，输出信号及其频谱的代码和波形如下：

subplot (1,2,1);

num=[2 0]; % 定义多项式分子

den=[1 2 10001]; % 定义多项式分母

t=linspace(0,12,1201); % 定义时间矢量t，0-12s之间共1201个线性等分点

x=cos(100*t)+0.5*cos(101*t)+0.5*cos(99*t);

% 计算输入函数

[y,x]=lsim(num,den,x,t); % 在 t时刻计算对输入x的响应

plot(t,y); % 输出绘图

xlabel('Tim e (s)');

ylabel('Amplitude');

title('Output Signals');

grid;

subplot (1,2,2); % 下一个图位于位置（1,2）

N=length(y);

y_f=fft(y); % 对信号y实行快速傅里叶变换

l=0:N-1; % 时间序列

k=(100/N)*l; % 频率序列

stem(k,abs(y_f))% 绘制幅度谱图

xlabel('frequency in Hz')

title('Spectrum of Signal');

grid;

输出响应是系统在调幅波激励下产生的零状态响应，包含暂态和稳态分量.从图3(a)可以看出，从第二个波包开始，输出趋于稳定，说明暂态分量基本消失.稳态响应的输出仍然是调幅波，但整体相对于输入信号向右偏移0.8左右，幅度相对于输入信号有所衰减.跟输入信号相比，输出信号的频谱（图3(b)）位置并未改变，频谱的峰值也在16Hz左右，幅度基本与输入信号中该频率成分一致，另外两种频率成分对应的角频率分别为99、101rad/s，幅度明显小于100ras/s处频率的一半.这些结论跟教材中得出的如下稳态响应表达式是完全吻合的.

图3 (a)输出信号的波形；(b)输出信号的频谱

1.4 根轨迹

根轨迹是开环系统某个参数沿正实轴从零变化到无穷时，闭环系统特征方程式的根在s平面上的轨迹.它是一种利用几何手段分析和设计线性时不变系统的方法.一个常见的例子是当开环增益改变时跟踪闭环系统的极点在复平面上的变化.例如，图4所示的反馈系统中，闭环增益由H(s)=A(s)/[1+KA(s)]给出.

图4 比例负反馈系统框图

上式中A(s)一般是s的有理分式，MATLAB提供了一个叫“rlocus”的函数计算根轨迹.假设A(s)=2s/(s2+2s+10001)，则相应的程序代码和根轨迹图如下：

num=[2 0];

den=[1 2 10001];

rlocus(num,den)%画根轨迹

xlabel ('Re(s)');

ylabel ('Im(s)');

title('Locus of Roots');

从图5可以看出，根轨迹有两条.一条从-1+j100出发通过实轴上点-100然后沿实轴正方向终止于原点，另一条从-1-j100出发通过实轴上点-100然后沿负实轴终止于无穷远处.根轨迹中不在实轴上的部分一定关于实轴镜像对称.

图5 根轨迹图

2 结 语

《信号与系统》课程教学中引入MATLAB仿真可以大大改善课堂教学效果.我们以带通滤波器作为示例，展示了课程教学中几个关键性专题的MATLAB实现方法，不仅能够引导学生快速入门，还能够进一步加深学生对课程中最为重要的几个知识点的理解.