极小Frobenius范数广义双对称求解一类矩阵方程

张 峰

（安徽交通职业技术学院 航海系，安徽 合肥 230051）

0 引 言

在21世纪，数学不仅作为一门工具被其它科学领域所使用，数学引领着其它学科的发展.方程作为线性代数领域的基础核心问题，是通过在一定的函数约束条件下建立线性代数集合，利用所构建的矩阵集合求得矩阵方程的解.依照不同的矩阵方程亦或是利用不同函数约束条件，以更好地求得不同矩阵方程的最优解[1-3].在具有特定约束条件的矩阵集合中，矩阵方程解获取是数值代数中的主要内容，其在信号处理与数码处理的过程中具有重要的作用.由于矩阵方程的求最优解问题甚至是双对称解问题在有限元、参数识别以及线性最优控制理论等领域中起着决定性的作用，其进一步刺激了矩阵方程理论迅猛发展，故将能否求得矩阵方程最优双对称解的问题提升至数学计算领域最热门课题核心.因此，如何利用未知矩阵方程中所提供的特征值、特征向量与数据要求确定相应的方程矩阵集合，并利用集合中有效解的等价条件以及几何性质、表达式等设计出可行性计算方法作为研究一类矩阵方程的双对称求解核心.

范数作为线性代数与泛函分析内的所有矢量在其矢量空间中被赋予的不小于零的一个函数.而Frobenius范数则针对于矩阵函数来说，是矩阵中每个元素的平方和的开平方运算，更确切地说Frobenius范数就是衡量一类矩阵方程到其所对应的零矩阵方程之间的距离，类似于在二维空间中，平面内的某个固定点到其原点之间的直线距离即为固定点的Frobenius范数[4-5].Frobenius范数很好地衡量了该矩阵的大小.随着线性代数的不断发展，传统的矩阵方程求解方法不能更好地解决线性代数矩阵方程的极小范数中双对称解问题.文章利用在一类矩阵方程中引入Frobenius范数，利用Frobenius范数的特点将原矩阵方程中出现的广义逆问题成功转化为无约束条件求解问题，并进一步求出极小Frobenius范数的广义双对称解.

1 极小Frobenius范数广义双对称解求解设计

对于一类矩阵方程，近年来对其的研究较为丰富.在此部分文献中利用矩阵分解求出了此类矩阵方程的约束解、约束最小二乘解及其最佳逼近解.在以往的一类矩阵方程的极小Frobenius范数双对称解求解方法使用过程中，多使用此种迭代计算方法，得到最佳逼近解.但此种方法在使用的过程中，具有一定的不足.因此，在此次研究中就针对其不足，优化原有求解方法中的不足.为有效控制优化过程，设定对应的流程完成求解方法设计过程.

1.1 一类矩阵方程中心对称约束条件设定

设定矩阵表示为A∈Rn*n，Rn*n表示n×n阶实矩阵集合，在此矩阵运算过程中具有一定的约束条件，在此次研究中将约束条件设定如下：

如矩阵满足上述约束条件，则称此矩阵为中心对称矩阵[6-7].此矩阵中的n阶中心对称矩阵集合可写作CSRn*n.假设此矩阵中各元素满足约束条件，则称此矩阵为中心反对称矩阵.在此矩阵中的n阶反中心对称矩阵集合可写作CASRn*n.在此环节中，将对下述两个问题进行求解，具体问题如下所示.

设定研究对象矩阵为B∈Rn*n，C∈Rn*n,求得A∈CSRn*n,则有：

Xi表示已知矩阵，Ei表示未知矩阵,f(Z)表示连续可微凸函数.假设存在Z*=Rn*n，使得当且仅当Δf(Z*)=0.

如果（2）及约束条件成立，则说明，当前的函数的一类矩阵方程解是振动的，判定条件如下：

根据上述公式，设定ki表示n阶单位矩阵yn的第i列，i=1,2,…,n.则Tn可称为n阶单位矩阵，有=Tn.

通过文献研究可知，矩阵A∈CSRn*n成立的首要条件是Tn*Tn=A[8-9].其次，若A∈Rn*n，则有A+Tn*Tn∈CSRn*n.将上述约束条件整合处理，可得到下述公式：

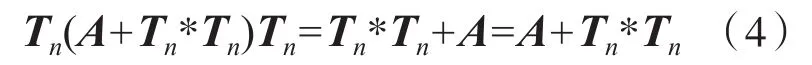
对上述公式进行分析可知，如果B,C∈CSRn*n,α1,α1∈ R,则α1B+α2C∈ CSRn*n.对此公式进行分析可知，CSRn*n为Rn*n的子空间.则有：

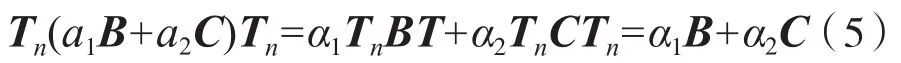
通过上述公式，对一类中心对称矩阵方程求解过程进行约束，且此方程必有中心对称解，此求解结果为一类矩阵方程的最小二乘解，即上述问题的解.将此结果作为下述计算过程的数据基础.由于矩阵问题常应用于结构力学、固体力学、结构设计等领域中[10-12]，在上述求解过程中根据应用环境设定取值方式，以此保证取值结果的可靠性.

1.2 矩阵方程迭代求解过程设定

使用上述设定的约束条件作为迭代求解过程的基础，将矩阵方程转化为方程组的形式，具体如下所示：

则矩阵函数的解可理解为方程组的解，由此可知，此方程组的最小二乘解[13-14]为矩阵方程解，将此方程组按列处理后，得到对应的线性方程组.定义(E,F,Δ)表示Menger PN空间，Δ为连续，那么概率分布函数f为下半连续，即随机t∈B，若n→∞存在qn→q、pn→p，那么：

通过上述公式可知，定义无限维Menger PN空间(E,F,Δ)中存在M开子集，随机t∈[0,1]，t-范数Δ符合以下要求：Δ(t,t)≥t.T:M→E为连续紧算子符合两点要求：

还原成公式（7）的形式，已知一类矩阵方程具有对应的数据解，则矩阵公式（7）也应具有数据解，为证实其具有数据解，设定此数据解为J，则有：

对上述公式等式两端进行转置处理，再进行较差减法可以得到对应的等式，也就是矩阵方程组（7）的数据解.根据公式（8）设定相应的迭代算法，对公式（7）进行求解.通过文献研究可知，在以往的研究中，对此公式解法的设计较为丰富，在此次研究中，将主要对矩阵的处理部分展开优化，以此提高数据运算能力.对于给定的一类对称矩阵，经过多次迭代后可以得到矩阵函数对应的解，由于矩阵方程有限维空间的限制，导致数据解序列进行正交处理，得到相应分量数列[15-17]，由于迭代处理中公式的等价性，使用此迭代方法得到的数据解可作为一类矩阵方程的极小Frobenius范数双对称解的数据计算来源，在接下来的处理中，将设定相应的计算过程得到极小Frobenius范数双对称解，完成方法优化过程.

1.3 广义双对称解逼近

根据上述设定的求解过程，考虑到方程组的广义双对称解情境.在此次研究中构造一个对应的求解过程.如果在1.2设定的迭代求解过程中可证实此矩阵方程组中具有广义双对称解[18-19]，则在不考虑计算误差的情况下，对于任意给定的初始一类矩阵方程，利用上文中设计的求解迭代算法，均可以在有限的迭代次数中得到对应的方程解.由此方法的迭代得到的数据解可视作矩阵方程组的极小Frobenius范数广义双对称解，因此，在此环节中将极小Frobenius范数双对称解逼近问题作为其求解过程，设定相应的方法完成基础运算，具体计算过程如下.

使用上述计算过程中得到的相容线性方程组[20]Ky=b的通解，定义条件设定t0≠0同时同α满足条件相斥，所以t0∈(0 ,1).结合公式（7）（8）得到公式（9）：

在上式中，z表示此方程组中的任意向量.由此同时可得到相应的范数解Q1、Q2，且此两组数据具有正交性，因此可知，K+b为上述方程组Ky=b的极小范数解.假设，且S为n阶中心对称方程，设定CSRn*n，使用上述中设定的迭代求解法能得到唯一的范数解，则此范数解可表示为：

根据此公式，在接下来的计算过程中证实此数据解为极小Frobenius范数对称解.通过公式（10）可知，上述公式具有中心对称解，因此只要证实此数据为公式（10）的最小范数解即可.使用传统的求解过程，得到矩阵方程的等价线性方程组，具体如下所示：

由上述公式可知，公式（12）是相容线性方程组的唯一极小范数解.对上述公式进行拉直映射同构处理可知，公式（12）为极小Frobenius范数双对称解.定义Menger PN空间(E,F,Δ)中存在开子集的紧性连续算子.当T符合如下要求时：

那么一类矩阵方程Tx=Jx+u在中有解.

由上可知，矩阵方程公式(13)具有相应的数据解，通过迭代算法可得到此公式的一个解.使用上述设定条件，可得到迭代问题中的唯一极小范数中心对称解，至此，求解计算过程结束.

将上文中设计部分进行整合，将其与原有的求解方法相结合.至此，一类矩阵方程的极小Frobenius范数广义双对称解求解方法设计完成.

2 实验论证分析

2.1 实验环境设计

在上文中完成了一类矩阵方程的极小Frobenius范数广义双对称解求解方法的设计过程，为验证此求解方法的计算效果，在此环节中对比文中设计方法与传统求解方法的使用效果，以此对文中设计方法展开全面的分析.为了提高实验效率，降低实验计算难度，使用计算机作为实验平台，完成数据计算处理过程.在此次实验中，选取高计算性能PC机作为实验平台，现将其参数设定如表1.

使用以上设定的实验平台参数，完成实验平台的组建过程.除上述设计的实验平台外，在此次实验中，涉及到大量的一类矩阵方程作为计算对象.在实验中共使用了1000个一类矩阵方程，将其每100个方程整合为一个方程实验组，使用文中设计方法与传统方法对其进行求解，并对相应的实验指标进行对比.

2.2 实验方案设计

在此次实验过程中，使用上文中设计的实验平台作为计算过程中的硬件基础.根据文中设计方法与传统方法的使用需求，在实验过程中，主要对此两种方法在计算过程中的迭代次数，方程式的逼近精准度以及计算响应时长作为实验的对照指标.通过文献研究可知，大部分的一类矩阵方程的极小Frobenius范数双对称解求解过程较为复杂且计算速度较为缓慢.因而，在此次实验过程中，对文中设计方法与原有方法的上述部分使用性能指标进行研究，通过上述指标的测试结果，分析文中设计方法与传统方法在使用中的差异.由于每个实验方程集合中具有多个方程，因此，将实验方程组的实验指标量化结果平均值作为实验最终结果.

2.3 计算迭代次数实验结果分析

由实验结果（图2）可知，在多个方程计算过程中，文中设计方法在计算中的迭代次数波动较小，且迭代次数基本控制在20次之内，具有较高的计算性能.与此同时，对图像进行分析可以看出，传统方法1 与传统方法2在计算过程中的迭代次数波动较大.使用统计学方法对上述实验结果进行分析可知，到实验结束时，文中设计方法的基础迭代次数为15次，且上下波动未超过5次，在实验的后期，此方法的迭代次数略有下降.传统方法1 与传统方法2的迭代次数均匀分布在25~30次之间，在部分方程组中具有小幅度波动的情况，可见此方法在计算过程中稳定性较差.通过文献研究可知，在求解过程，求解方法计算迭代次数对于计算结果的准确性具有直接的影响.因此，根据上述实验结果可知，文中设计方法的使用效果优于其他两种传统方法.

图2 计算迭代次数实验结果

2.4 方程式解逼近精准度实验结果分析

对实验图像（图3）进行分析可知看出，文中设计方法在求解过程中的逼近计算精准度较高，在使用的过程中可在较短的时间内完成计算过程，并得到相应的计算结果.相较于文中设计方法的使用效果，传统方法1与传统方法2在使用的过程中，对于方程式解的逼近精度较差，通过数据分析可以看出，在部分实验组中出现计算异常问题，由此可知此两种方法的使用效果较差.将此部分实验结果与计算迭代次数实验结果综合分析可知，文中设计方法的基础性能优于传统方法，根据此实验结果可初步判断文中设计方法的使用效果将优于传统方法.

图3 方程式解逼近精准度实验结果分析

2.5 方程式求解响应时长实验结果分析

根据上两部分实验结果可知，文中设计方法具有较好的使用效果，为了保证此次研究的全面性，在此部分中对方程式求解响应时长进行研究，通过此指标研究结果（图4）可以看出，文中设计方法的求解计算实验较短，随着实验次数的不断增加，文中设计方法的计算速度不断提升.与文中设计方法相比，传统方法1与传统方法2求解速度较慢，且随着实验次数的不断增加，此两种方法的计算速度出现下降的情况，可见此两种方法的计算能力较差，无法将其应用于大量的数据运算过程中.根据上述实验结果可知，文中设计方法的使用效果较为优异.

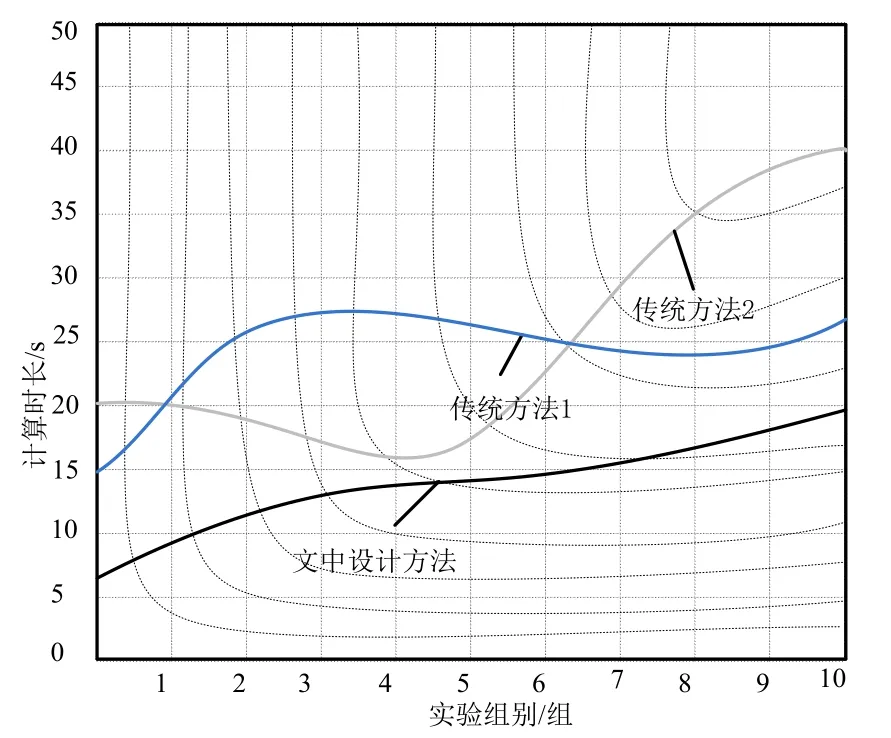
图4 方程式求解响应时长实验结果

将此次研究中得到的计算迭代次数实验结果、方程式解逼近精准度实验结果以及方程式求解响应时长实验结果进行整合分析可知，文中设计方法的使用效果优于传统方法.在日后的计算过程中，可使用文中设计方法作为主要方程式求解方法，提升一类矩阵方程极小Frobenius范数求双对称解求解速度与质量.

3 结束语

一类矩阵方程的极小Frobenius范数广义双对称解的问题就是在既定的矩阵集合中求得相容的该矩阵方程的双对称解或者可以说是不相容的方程中最小二乘解的过程.Frobenius范数定义了矩阵方程的长度性质，在满足行和范数的条件下，求得线性矩阵方程双对称解向量绝对值之和的最大值.通过矩阵方程的相关度量性构建方程实际结构信息，并利用线性矩阵方程间各行的强关联性，将方程投影到更低维度的线性矩阵方程子空间，简化方程的线性表达向量，并通过低秩矩阵对冗余信息进行数据修复，进而对数据进行特征提取.通过对上文关于一类矩阵方程的极小Frobenius范数广义双对称解问题的研究，虽然Frobenius范数能有效地将矩阵方程逼近问题进行分析研究，但很难验证其与非凸函数甚至其他矩阵范数之间的双对称解问题，需要在今后的研究中针对这一问题进行更深层次、更系统的理论研究.