生物听觉耦合机制的矢量组合阵方位估计方法
2021-07-13方尔正桂晨阳孙纯陈峰王欢
方尔正,桂晨阳,孙纯,陈峰,王欢
(1.哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;2.海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学),黑龙江 哈尔滨 150001;3.哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)
水下目标方位估计是水声阵列信号处理的重要研究方向之一,通常在空间分布若干传感器采集声场中的信号信息,然后利用方位估计技术提取信号的来波方向(direction of arrival, DOA)。常用的目标测向技术有基于常规波束形成(conventional beamforming, CBF)和最小方差无畸变响应(minimum variance distortionless response, MVDR)波束形成的DOA估计算法,以及子空间类DOA估计算法[1]。
随着海洋国防科技的快速发展,基于水下潜器的自主作战平台已经成为各国海军的重要发展领域之一。为了提高水下无人机的隐蔽性和灵活性,其工作平台尺度越来越小,所搭载的声呐阵列孔径也随之变小,基于小孔径阵列的目标探测技术已然成为未来海洋军事发展的重要内容之一。水声工程实践场景中,常会遇到阵列空间有限制的情况,为了提高小孔径阵列的DOA估计性能,通常采取的方法是虚拟阵元技术和合成孔径技术。前者通过不同阵元数据拟合,虚拟出新阵元扩展阵列,但是虚拟阵元信号与真实阵元信号相关性较高,无法带来较高信噪比收益,因此适用于高信噪比情况[2]。后者是在平台缓慢地匀速运动时,虚拟不同位置阵元,提高目标探测性能,主要针对匀速运动平台[3-4]。倘若在小平台直接搭载远小于信号波长的阵列,阵元间相位差较小,导致CBF和MVDR方法的波束宽度过宽,阵增益较小,无法有效分辨水下多目标。
奥米亚寄生蝇的独特听觉机制为解决这一问题提供了新方向。奥米亚寄生蝇的双耳距离约为1.2 mm,而蟋蟀叫声的波长约为7 cm远远大于双耳距离,但奥米亚寄生蝇却能依靠听觉定位寄主蟋蟀的位置进行寄生。Miles等[5]对奥米亚寄生蝇的听觉系统展开了研究,揭示了奥米亚寄生蝇可以精确定位蟋蟀位置的原因,建立了一个机械耦合模型模拟寄生蝇的双耳听觉系统结构。基于此机械耦合模型,开展了仿奥米亚寄生蝇听觉系统的声源定位、超短传感器阵列制作等研究内容[6-9]。然而,该耦合机制在放大信号的同时也将噪声同等放大,导致在低信噪比条件下该方法的DOA估计算法估计性能欠佳[6]。
矢量传感器可同步共点的拾取声场中一点的声压和2个或3个相互正交的振速分量。相比传统的声压传感器,矢量传感器可获得更丰富的信息。文献[10-13]的研究表明,对于有限尺度的声源,在其远程声场,矢量传感器接收的声压与振速信号是相干的,而对于各向同性噪声场互不相关,从理论上揭示了声强方法具有抑制噪声能力。
本文受声强和奥米亚寄生蝇听觉系统启发,提出了仿生物听觉系统机制的小孔径矢量组合阵列的DOA估计方法。本文采用一只矢量传感器若干声压传感器设计了一小孔径矢量组合阵列,设计了一种声强滤波器,结合奥米亚寄生蝇听觉结构,将其拓展至多元小孔径阵,推导出了耦合矩阵的具体表达式,最后利用CBF和MVDR方法获得了空间谱图,并进行仿真验证所提方法的有效性。
1 组合阵接收信号模型
本文研究的是小孔径矢量组合阵的方位估计问题。如图1所示,组合阵由2U只标量传感器和1只矢量传感器组成,阵元间距为d,矢量传感器位于坐标原点为“0”号阵元,原点两侧各布放U个声压传感器,分别用“-U,…,-1”和1,…,U进行标号。假设K个不相关单频信号s1(t),…,sK(t)分别从θ1,…,θK入射至矢量线阵,以坐标原点为参考点,则在t时刻,M元组合阵的接收数据可表示为(M=2U+1):
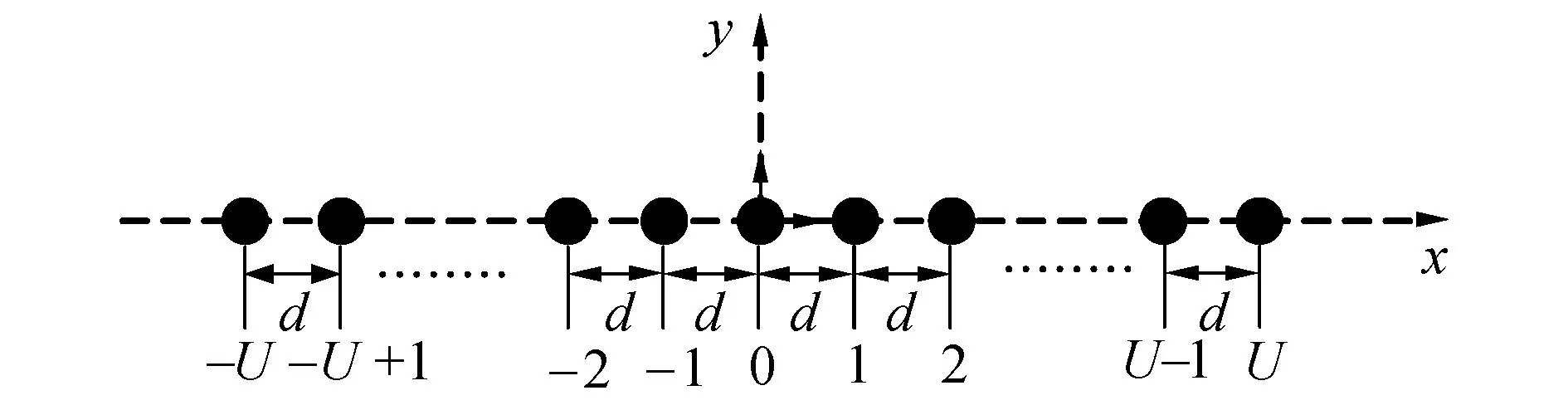
图1 矢量组合阵模型
(1)
式中:s(t)=[s1(t),s2(t),…,sK(t)]T表示K×1维信号向量;p(t)表示M×1维组合阵声压通道接收的数据;vx,0(t)和vy,0(t)表示1×1维矢量传感器的2个振速通道接收数据;np(t)表示M×1维零均值的高斯白噪声,各传感器的噪声互不相关,且与信号也不相关;nx,0(t)和ny,0(t)表示矢量传感器2个振速通道接收的噪声;A(θ)=[a-U(θ),…,a-1(θ),a0(θ),a1(θ),…,aU(θ)]T表示M×K维矢量阵声压分量的导向矢量矩阵。则标号为m的传感器对应的导向矢量可表示为(m=-U,-U+1,…,U):
am(θ)=[am(θ1)…am(θk)…am(θK)]
(2)
式中:am(θk)=ej2πmdcos θk/λk;λk=c/fk表示第k个单频信号的波长;c表示水下声速;fk表示第k个信号的频率。
式中:ux和uy分别表示x、y振速分量的方向矢量,可表示为:
(3)
2 矢量声强滤波器的设计
本节基于矢量水听器设计了矢量声强滤波器,然后对组合阵的声压通道数据进行滤波。
首先,将矢量阵接收的p0(t)、vx,0(t)和vy,0(t)做时域傅里叶变换,有:
(4)
式中:P0(f)、Vx,0(f)和Vy,0(f)分别表示p0(t)、vx,0(t)和vy,0(t)的傅里叶变换;S(f)表示傅里叶变换后的信号矢量;Np(f)、Nx(f)和Nx(f)表示噪声的傅里叶变换。
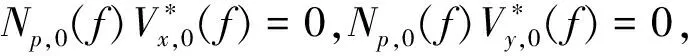
(5)
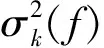
根据文献[12],可得到广义互相关滤波器,:
(6)
根据式(6),可得应用于声压阵的滤波器:
Hz(f)=Hs(f)IM
(7)
式中IM表示M×M维单位矩阵。
利用上式求得的滤波器对组合阵声压通道进行滤波,可得滤波后的声压阵列的频域信号:
(8)
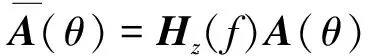
3 仿生物听觉耦合算法
3.1 寄生蝇双耳耦合机制
如图2所示,x1(t)和x2(t)表示蟋蟀声波达到耳朵两侧鼓膜的声波信号;y1(t)和y2(t)是奥米亚寄生蝇听觉耦合响应后的信号,在机械系统中模拟的是鼓膜的位移;奥米亚寄生蝇的鼓室建模为2个刚性桥;m0为质量块模拟双耳两侧运动部分;奥米亚寄生蝇鼓膜和周围结构的动力学特性分别用2组弹性和阻尼系数(α1,β1)、(α2,β2)模拟;鼓膜膜间桥用弹性和阻尼系数(α3,β3)的耦合连接2个刚性桥。当两侧鼓膜的声波信号使鼓膜振动,鼓膜将发生位移,该机械耦合系统受到了弹性力、阻尼力以及惯性力的作用,其运动方程可表示为:
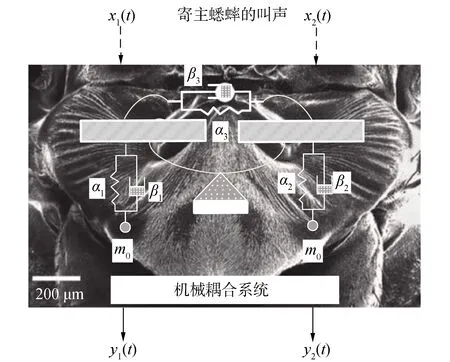
图2 奥米亚寄生蝇双耳机械耦合系统[8]
(9)
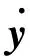
对式(9)进行傅里叶变换,可得到:
(10)
其中:
引入变量:
(11)
将式(11)代入式(10),可得:
(12)
其中:
通常情况下寄生蝇双耳为对称,即α1=α2=α0,β1=β2=β0,因此D1(f)=D2(f)、B4(f)=B2(f)、B3(f)=-B1(f)、以及G(f)=2B1(f)B2(f)。以双耳中心为参考点,设x1(t)=ejπfτ,x2(t)=e-jπfτ(τ为两耳接收信号的时延差),则双耳输出响应可表示为:
(13)
式中:τ=dccosθs/cc;dc=1.2 mm为双耳距离;cc≈344 m/s为空气声速;θc表示声波入设角度。
图3、4给出了耦合后(信号Y1(f)、Y2(f))和没有耦合(即双耳接收信号X1(f)、X2(f))的幅度以及相位随频率的变化关系,其中入射角度为45°。从图3、4可以看出,经过寄生蝇双耳耦合放大系统后的2个信号幅度和相位的差别明显增大,说明了该耦合放大系统增大了到达两耳信号的幅度和相位差(等效于扩大双耳间距)。
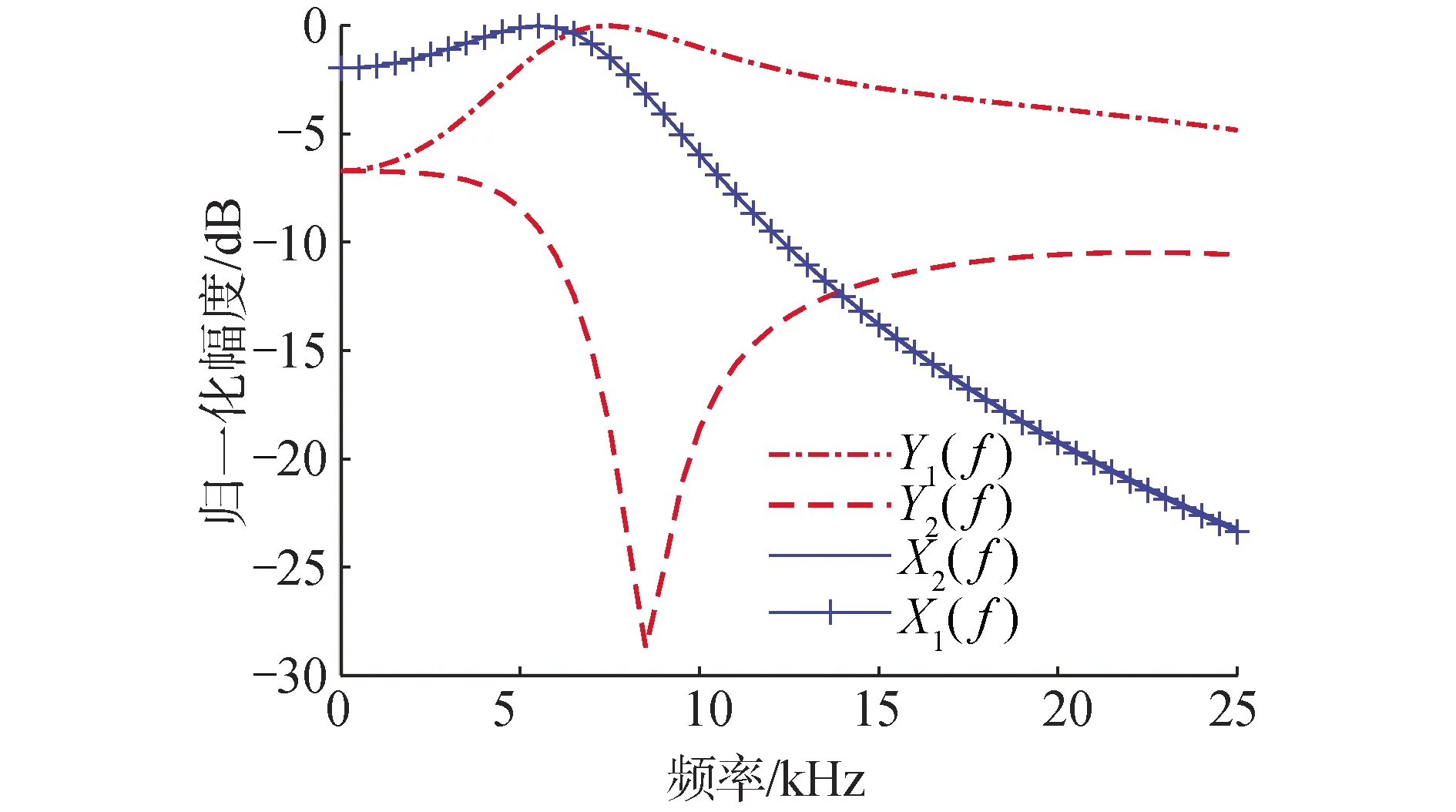
图3 寄生蝇双耳耦合和非耦合归一化幅度随频率的变化
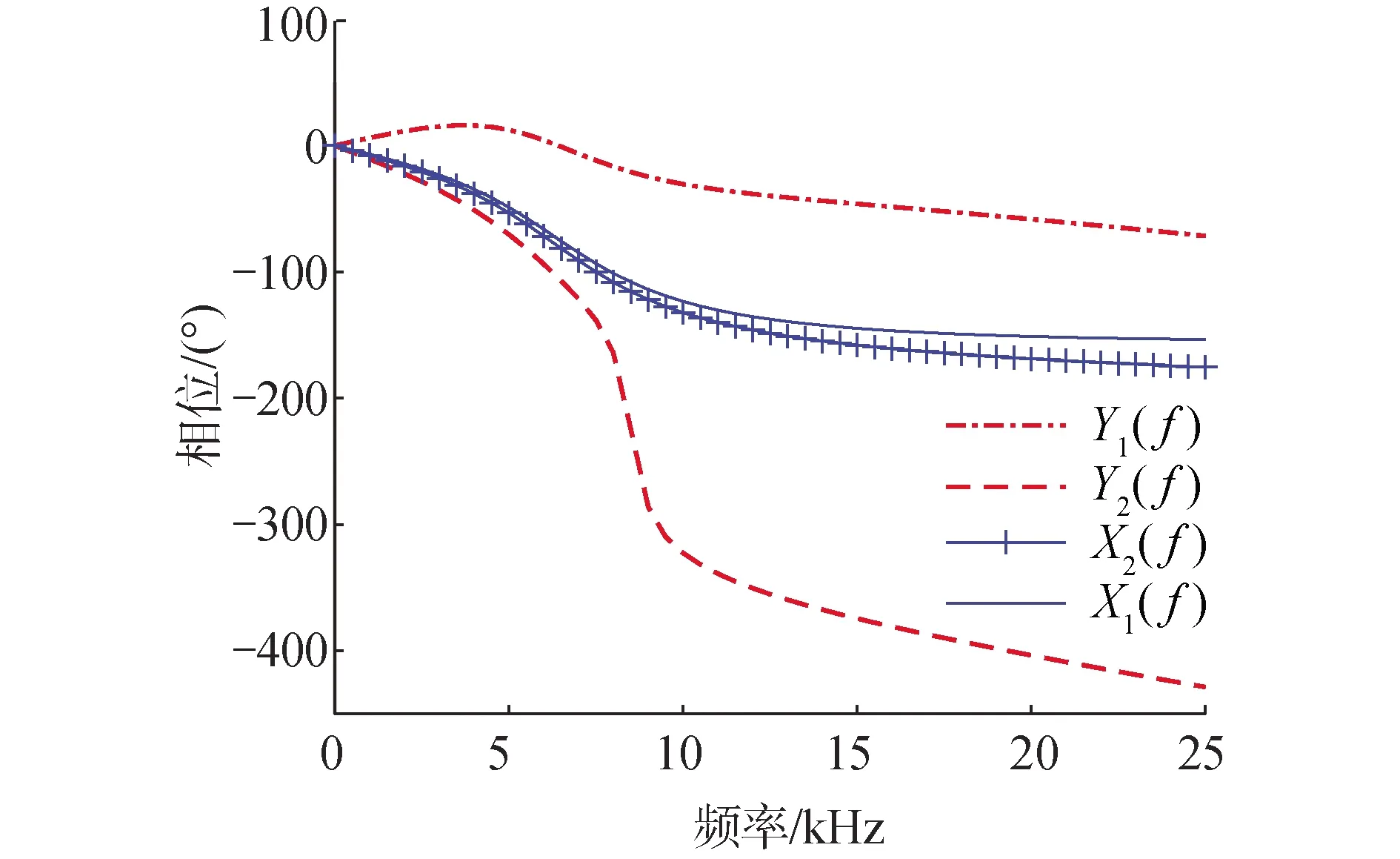
图4 寄生蝇双耳耦合和没有耦合的相位随频率的变换
3.2 多元线阵耦合放大矩阵
本文根据上述原理,将寄生蝇双耳耦合系统推广至多元线阵。通过寄生蝇耦合方法对广义矢量滤波后的信号进行耦合处理,增强2个相邻阵元的。
根据式(13)不难发现,二元传感器阵列的耦合放大矩阵的具体表达形式为:
Tc(f)=Hc(f)Λc
(14)
式中Hc(f)、Λc为2×2维矩阵,分别为:
其中:Γ(f)=α0+2α3+j2πf(β0+2β3)-m0(2πf)2,Υ(f)=α0+j2πfβ0-m0(2πf)2。
3.3 线阵耦合DOA算法
式(14)给出了相邻2个阵元的耦合放大矩阵的具体表达式,下面针对M元线阵,推导出相应的耦合放大矩阵。具体做法为:以相邻的2个阵元为一组将M元线阵分成N=M-1组,根据式(14)可以得到N组耦合放大矩阵,假设M元传感器的幅度、相位响应均一致,则N组耦合放大矩阵也是相同的,因此,将这些耦合放大矩阵合并,可以得到M元线阵的耦合放大矩阵TM为:
TM(f)=H(f)Λ
(15)
式中H(f)和Λ分别为2N×2N和2N×N矩阵,具体为:
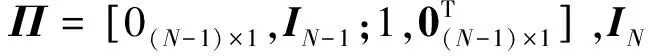
将式(15)左乘式(8),便可得到经过耦合放大的阵列接收信号:
(16)
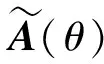
(17)
根据式(17),可以得到耦合放大的阵列信号协方差矩阵:
(18)
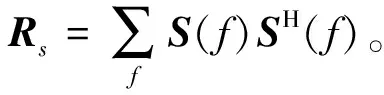
(19)
式中θl表示空间扫描角度。由于奥米亚寄生蝇的听觉耦合系统不仅增加了相位差,同时也增加了幅度差,为了降低幅度影响,对导向矢量进行去模处理为:
(20)
(21)
4 小孔经空间谱算法仿真
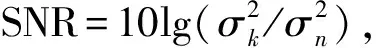
4.1 单目标空间谱对比分析
图5给出了不同入射角度单目标的CBF和MVDR空间谱估计结果。信号频率为1 000 Hz。信噪比为-10 dB。从图5可以看出,传统CBF和MVDR方法的旁瓣级都大于-3 dB,主瓣宽度很大。相比之下,基于本文所提方法的CBF和MVDR方法的旁瓣级很低,而且主瓣宽度较窄。产生这种现象的原因主要是本文设计了矢量声强滤波器抑制了声压阵列的噪声,然后又引入了生物听觉系统的耦合放大机制放大了相邻阵元的相位差。
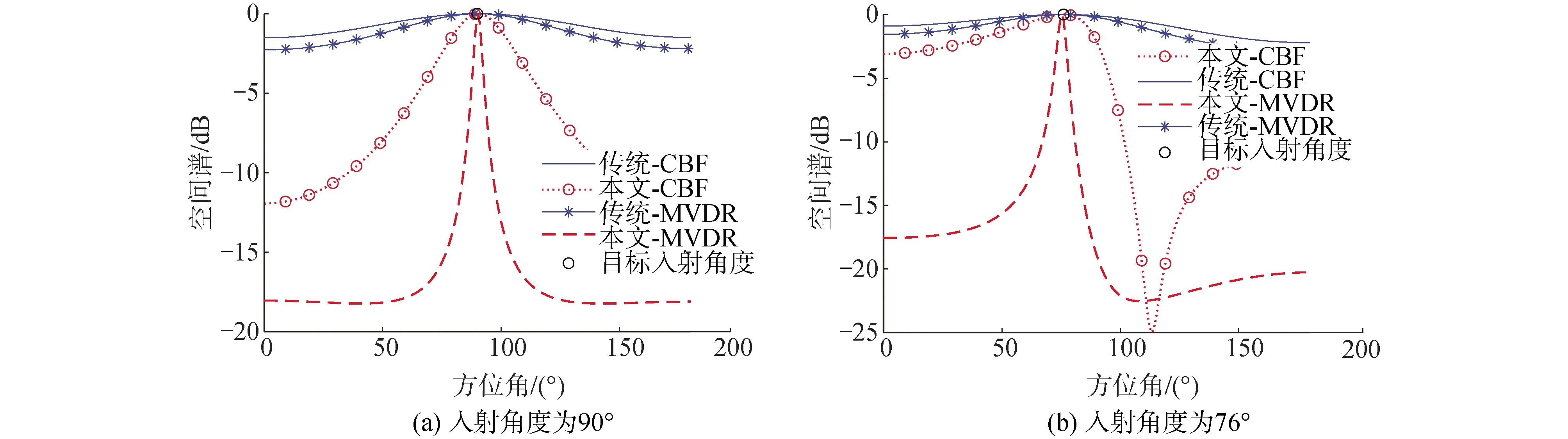
图5 不同入射角度的单声源空间谱结果
4.2 多目标空间谱对比分析
图6(a)给出了2个不相关等幅信号的CBF和MVDR空间谱估计结果。信号频率分别为1 000、980 Hz,入射角度分别为70°和110°,2个信号的信噪比均为15 dB。从图5(a)可以看出,传统CBF方法无法分辨2个不相关信号的来波方向,而本文所提CBF方法有2个谱峰,可分辨2个不相关信号,但方位估计误差较大。尽管传统MVDR估计的空间谱有2个谱峰,但谱峰高度太低,且方位估计误差较大,相比之下本文MVDR方法估计空间谱有2个超过25 dB的谱峰,可有效分辨2个不相关信号,而且方位估计精度较高。
图6(b)给出了3个不相关目标的CBF和MVDR空间谱估计结果。信号频率分别为1 000、980和1 080 Hz,对应的入射角度分别为55°、80°和110°,信噪比分别为15、15和9 dB。从图可以看出传统CBF、MVDR以及本文CBF方法都无法分辨3个不相关信号,相比之下本文MVDR方法有3个谱峰,可以分辨3个不相关信号,而且方位估计精度较高。
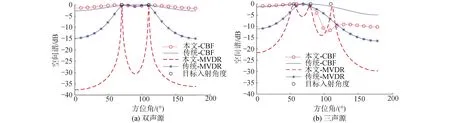
图6 多目标的空间谱结果
本节仿真结果表明本文所提方法相比传统方法更适合应用于水下小平台的多目标测向。
4.3 方位估计性能分析
本节通过200次蒙特卡罗仿真实验分析传统CBF、MVDR方法与所提CBF、MVDR方法的目标测向的均方根误差和目标分辨能力。
4.3.1 测向精度
本节采用的均方根误差定义为:
(22)
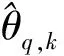
图7给出了入射角度为90°和50°的单目标方位估计的RMSE随信噪比的变化情况。从图7可以看出,随着信噪比的增加,CBF和MVDR方法的均方根误差逐渐减小,而且传统CBF、MVDR与本文所提CBF、MVDR方法在相同信噪比条件下方位估计精度几乎相等。对比图7(a)和图7(b)可以发现,当入射角度偏离阵列法线方向时,CBF和MVDR的测向结果变差,但对本文MVDR和传统CBF和MVDR的影响较小。尽管仿生学的耦合机制在放大信号的同时也放大了噪声,本文在耦合放大技术前加入的矢量声强滤波可以减弱耦合放大技术对噪声的放大作用,因此,所提方法在低信噪比条件下仍可保持较好的估计精度。
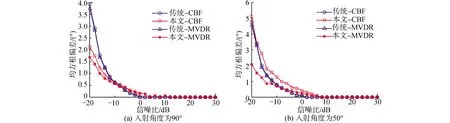
图7 不同入射角度单声源的测向RMSE随信噪比的变化情况
图8给出了CBF和MVDR方法对2个等幅目标测向RMSE随信噪比的变化情况。2个不相关信号频率分别为1 000和980 Hz,入射角度分别为70°和110°。从图8可以看出传统CBF方法的均方根误差一直为20°,说明传统CBF方法始终只有一个谱峰;随着信噪比的增加,传统MVDR和本文所提CBF和MVDR方法的均方根误差逐渐减小;而且本文CBF相比传统CBF具有较高的DOA估计精度,类似地,本文MVDR相比传统的MVDR具有较高的DOA估计精度;此外由于MVDR分辨力较高,因而本文MVDR方法较本文CBF方法具有更高的方位估计精度。
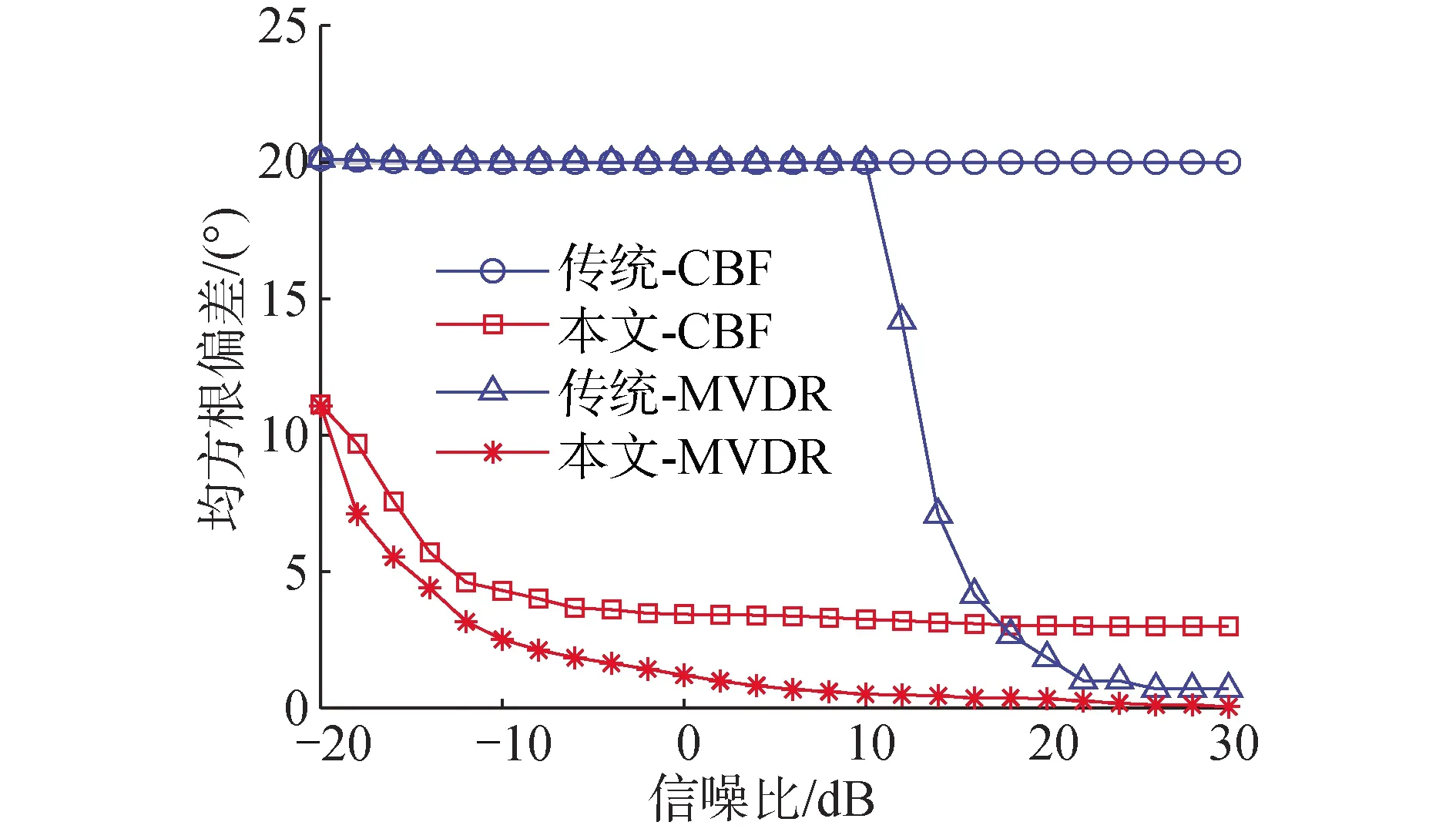
图8 入射角度为70°和110°的双声源测向误差随信噪比的变化情况
本节仿真结果说明在单目标情况下本文所提CBF、MVDR方法与传统CBF和MVDR方法的测向精度近似相同,但在多目标情况下,本文所提CBF和MVDR的测向精度要优于传统CBF和MVDR方法。
4.3.2 目标分辨能力
图9给出了双目标情况下CBF和MVDR方法的目标分辨概率随2个信号入射角度间隔的变化情况。2个不相关信号频率分别为1 000 Hz和980 Hz,入射角度分别为60°和60°+Δθ,Δθ从0°以3°为间隔变化至60°,信噪比为15 dB。从图9可以看出,传统CBF方法无法分辨2个不相关信号;本文的CBF方法在角度间隔不小于42°时便可分辨2个信号;传统MVDR在角度间隔不小于39°时才可完全分辨2个信号;相比之下本文MVDR方法在角度间隔达到15°时便可100%分辨2个目标。
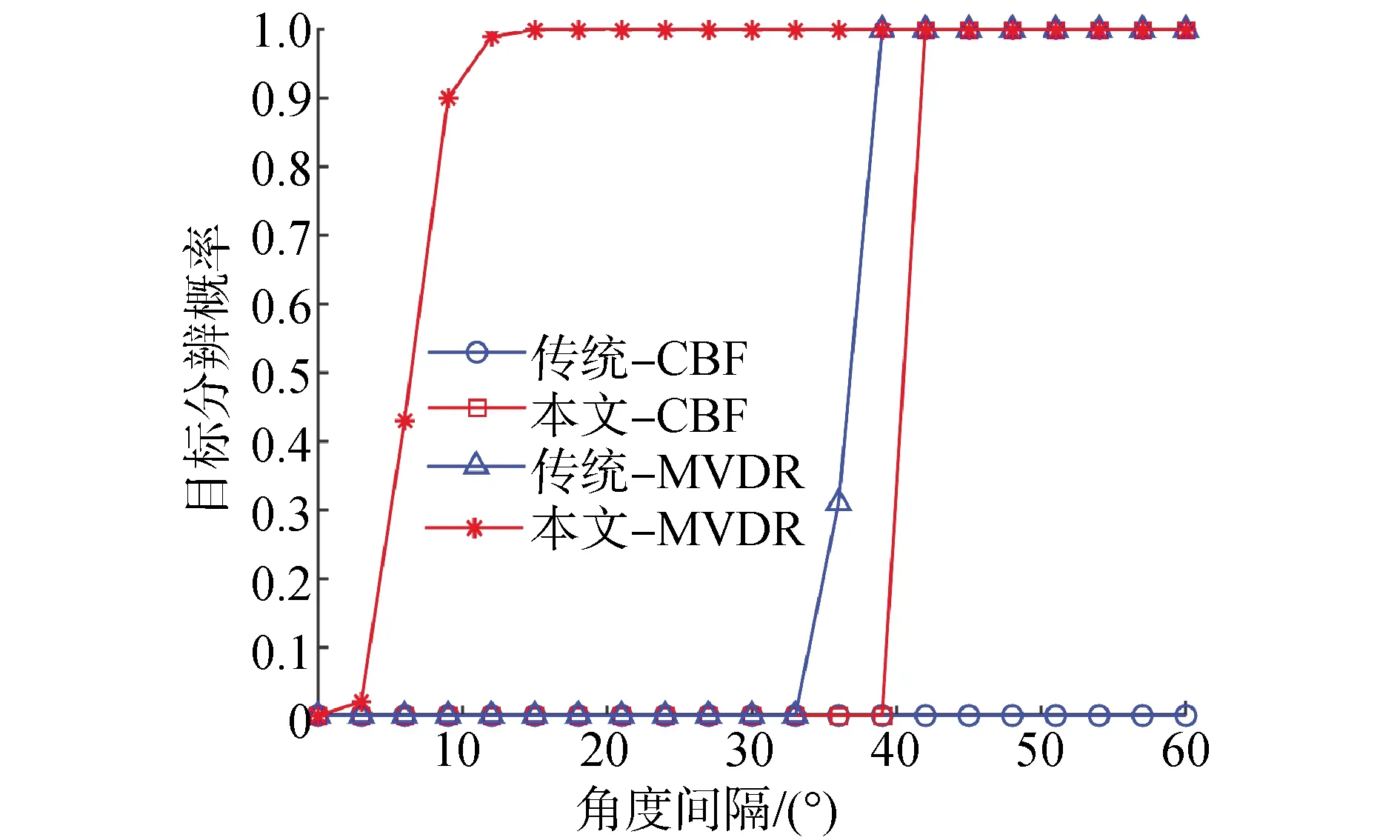
图9 双目标分辨概率随角度间隔的变化
本节仿真结果说明本文所提CBF、MVDR方法较传统方法具有更高的目标分辨能力,而且本文所提MVDR相比其他方法的目标分辨能力更强。
5 结论
1)本文通过利用设计的矢量声强滤波器抑制了各向同性噪声,提高了组合阵声压通道接收信号的信噪比,使所提CBF和MVDR方法在较低信噪比条件下仍可保持较好的DOA估计精度。
2)本文所提CBF和MVDR方法有效的结合了矢量声强滤波器的抑制噪声能力和寄生蝇听觉系统的耦合放大机理,与传统的CBF和MVDR方法相比,具有更低的旁瓣,更高的测向精度和目标分辨能力。
本文仅对小平台中的单频信号的DOA估计问题进行了研究,而水下信号还包括宽带信号,又因为耦合参数选取与频率息息相关,因此小孔径阵的宽带信号DOA估计问题是下一步要研究的内容。
