海底管道动态压溃时激发压力脉冲特性分析

2021-07-13付光明李明亮孙宝江高永海刘树阳时晨

哈尔滨工程大学学报 2021年7期

付光明，李明亮，孙宝江，高永海，刘树阳，时晨

(1.中国石油大学(华东)石油工程学院，山东青岛 266580; 2.中国石油大学(华东)，山东省油气储运安全重点实验室，山东青岛，266580)

管道压溃是外压作用下的非线性动态行为，是深水管道最为常见的失效形式。压溃发生后，压溃变形将以数百米每秒的速度沿管线传播，导致数公里甚至数百公里管道的损坏[1]，与此同时，管道压溃将激发数倍于压溃压力的脉冲压力，该压力脉冲将损伤周围管道，引起重大安全事故[2-3]。

近年来，国内外学者对水下爆炸和结构压溃变形等激发压力脉冲问题做了大量研究，Turner等[4]利用实验手段研究了铝管的压溃问题，实验中观察到与玻璃球压溃实验[5]中相似特性的压力脉冲，并指出压溃材料的失效时间历程对压力脉冲特性有显著的影响。Netto等[1]研究表明水的压缩性对压力脉冲起着重要作用，并利用近似流固耦合模型计算了压溃传播速度。Farhat等[3]研究了压溃模式对压力脉冲的影响，更高的压溃模式会产生更高的压力峰值，但与较低的压溃模式相比，持续时间更短。Ikeda等[6]对不同几何形状的黄铜结构进行了实验研究，研究了不同压溃模式下压力脉冲的特点。Gupta等[2]通过管道压溃试验研究表明，压力脉冲会对管道产生较强破坏，并测量了管道的动态压力，探讨了压溃开始时压力脉冲的演变规律。DeNardo等[7]探讨了复合无粘结夹层结构压溃过程中的屈曲和流固耦合效应。Kishore等[8]实验研究了充填不同密度聚氯乙烯泡沫的碳纤维/环氧树脂壳的水下压溃模式、压溃速度、压溃变形的径向位移等变化规律。Cor等[9-10]研究了球形和圆柱形压溃体积以及内部结构对压溃压力脉冲的影响,并指出内部结构可以显著降低压溃压力脉冲。Gish等[11]提出了一种用已知总势能与塑性变形损失能量之差来估计压力脉冲能量的方法，并指出压溃脉冲能量与系统压溃过程中产生的最大动能成正比。Michael Pinto等[12]对碳纤维增强环氧复合管的静水压溃进行了实验研究，探讨了其独特的压溃破坏机理。余建星等[13-14]利用自主研制的深海压力舱，进行全尺寸管道压溃试验，讨论了动态加载及准静态加载条件下管道压溃及动态屈曲传播行为。姚熊亮等[15-16]基于ABAQUS数值模拟平台，采用声固偶合技术研究了水下爆炸冲击波与结构的耦合行为。龚顺风等[17]通过深海压力舱小比例模型试验，研究了层间黏结性能对夹层管屈曲传播的影响。雷明玮等[18]、龚顺风等[19]利用有限元软件ABAQUS建立了夹层管复合结构在外压及纯弯作用下的三维数值模型，分析了外压及纯弯作用下夹层管复合结构屈曲失稳问题。

目前针对深水海底管道压溃激发压力脉冲的时空分布特征以及该压力脉冲与压溃传播的耦合规律的研究较少。本文建立了深水海底管道动态压溃传播的有限元数值计算模型，并利用文献中的实验结果验证了本文有限元模型的正确性。利用声固耦合技术模拟海底管道与周围流体介质的耦合作用，分析了管道周围压力脉冲的时空分布规律以及海底管道压溃传播过程中压溃变形与压力脉冲的耦合特性。讨论了海底管道发生翻转(Flip-Flop)型压溃传播时，管道周围压力脉冲的分布规律。

1 有限元模型

1.1 基本假设及载荷和边界条件设置

本文建立了管道动态压溃1/4有限元模型，如图1所示。其中，管道单元类型为8节点6面体单元(C3D8I)，基于声固耦合分析方法，采用声单元AC3D8模拟管道周围流体介质，流体外边界设置无反射界面模拟无限流体环境。流体内边界和管道外边界分别定义2个平面，并通过“TIE”的约束方式设置声固耦合界面，实现结构位移场和流体压力场的耦合。有限元模型长度不少于10倍管径。模型中设置刚性接触面I和II，用于模拟管道压溃后的内壁面的接触行为。管道轴向和周向满足初始椭圆度分布式[1]：

(1)

式中：ωo为极坐标系下径向位移，mm；Δ为管道初始椭圆度，Δ=(Dmax-Dmin)/(Dmax+Dmin)；x为轴向方向坐标；β为初始椭圆度在x轴向延伸的相关系数；θ为极坐标下的角度；D为管道直径，mm；Dmax为椭圆长轴长度，mm；Dmin为椭圆短轴长度，mm。

建立边界条件如图1所示：在管道对称平面上分别施加关于平面XOY、XOZ和XOY的平面对称约束；在管道另一端面上约束Y和Z方向的平动位移。管道外界面和液体内界面通过定义“Tie”的接触属性模拟管道与其周围流体的耦合效应。

图1 有限元模型和边界条件

动态压溃数值模拟过程包括：1)静态压溃分析过程，在管道外表面施加均布压力，利用Riks方法，获得管道的压力变化曲线，如图2所示，其中，Pco为压溃压力，Pi为进行动态压溃传播分析的初始压力，Pp为管道的屈曲传播压力。2)动态压溃分析过程，通过重启动计算技术，获得静态分析1)中的管道的应力和变形状态，并在(0,0,0)位置处施加微小扰动，如图1所示。在动态分析步中施加初始压力Pi，设置时间增量步为10-6s，进行动态压溃传播分析。

图2 管道动态压溃传播压力曲线

1.2 有限元模型的验证

选取文献[3]中室内压溃实验对本文的有限元模型进行验证。实验管道铝管结构尺寸为：直径为38.2 mm，长径比L/D为8，壁厚为0.711 mm，利用高速相机和PCB 138A06 ICP电气石水下冲击波压力传感器同步记录管道的压溃变形过程和压力脉冲情况。具体实验过程参见文献[3]。

管道压溃的数值模拟结果为1.37 MPa，与实验结果1.36 MPa误差为0.74%。该管道压溃后的变形形态为扁平型。图3(a)表示本文数值模拟求得管道压溃形态和实验获得的压溃形态结果比较，图3(b)为本文计算得到的压溃变形形态的演化过程和实验结果[3]的比较，通过比较可知，本文建立的数值模型可以合理预测管道不同阶段的动态压溃行为。图4为压溃过程(持续1.5 ms)中传感器1、传感器5和传感器7记录的压力脉冲的演化规律以及压溃过程中压溃变形(1)～(10)对应的压力脉冲。

图3 本文数值模拟结果与实验结果[3]比较

图4 初始压溃界面不同位置处压力脉冲分布规律

由图4可知，由于管道的压溃引起管道周围负压力脉冲的产生。其中，径向距离管道1D位置处，该负压力峰值大小约为0.5 MPa；管道压溃后内壁面发生碰撞，与此同时，该位置处管道周围的液体与管道发生碰撞，进而将激发正压力脉冲，该压力脉冲峰值约为1.8 MPa，高于管道的压溃压力1.36 MPa。文献[3]给出了该压力脉冲的实验和解析结果，利用本文有限元模型计算得到压力脉冲随时间变化曲线如图4所示。通过比较得知，本文计算得到的传感器1号的压力脉冲峰值为1.2 MPa，与实验测得结果1.8 MPa有较大的差别，但与文献[3]中解析结果1.36 MPa较为接近。通过分析原文献得知，该位置处管道壁厚存在偏心，而有限元数值模型中未考虑管道壁厚偏心的影响，导致该位置处压力脉冲峰值的数值模拟结果和实验结果在有较大偏差，但压力脉冲随时间的变化趋势一致。本文计算求得5号和7号传感器位置处压力脉冲峰值分别为1.38 MPa和0.56 MPa，与文献中实验结果[3]分别相差1.47%和10%，在该传感器位置处，数值模拟求得的压力脉冲峰值和随时间的变化规律与文献中的实验和解析结果的分析结果较为接近。通过与文献结果的比较，本文建立的有限元模型可以合理地预测外压作用下管道动态压溃压力、压溃变形形态和压力脉冲的演化过程。

2 动态压溃变形与压力脉冲

2.1 管道几何与材料参数

选取API-5XL[20]规范中X65管道作为研究对象，具体几何结构参数如表1所示。材料弹性模量为207 GPa，泊松比为0.3，屈服强度为448 MPa。考虑各向同性强化的弹塑性本构模型，分析外压作用下管道压溃行为和压力脉冲的时空分布规律。本文采用管道压溃压力作为动态压溃分析的初始压力，分析管道在压溃压力作用下管道的动态压溃变形与压力脉冲的变化规律。

分别采用DNV-OS-F101规范[21]计算压溃压力(Pco-ana)和压溃传播压力(PP-ana)：

(2)

Pp-ana=35σ0αfab(t/D)2.5

(3)

其中：

Pel(t)=2E(t/D)3/(1-v2)

Ppr(t)=2σ0αfabt/D

f=(Dmax-Dmin)/D

式中：D为管道直径，mm；t为管道壁厚，mm；Dmax为椭圆长轴长度，mm；Dmin为椭圆短轴长度，mm；pco为管道压溃强度，MPa；pp为管道压溃传播强度，MPa；Pel、Ppr和f为辅助计算参数；E为弹性模量，GPa；υ为泊松比；αfab为管道的制造系数，本文取1。

如表1所示，本文有限元模型计算得到的管道压溃压力结果与解析计算结果的最大误差为6.89%，压溃传播压力的模拟结果与解析结果的最大误差为4.88%，该有限元模型满足计算精度要求。

表1 管道几何参数及压溃压力数值模拟结果与经验公式计算结果对比

2.2 海底管道压溃动态压力脉冲变化规律

2.2.1L/D=10时压力脉冲变化规律

图5为工况4条件下管道动态压溃的分析模型和管道压力的变化曲线。由计算可知，该管道的压溃压力和压溃传播压力的有限元计算结果分别为65.63 MPa和25.33 MPa。如表1所示，该有限元计算结果与解析计算结果较为吻合。

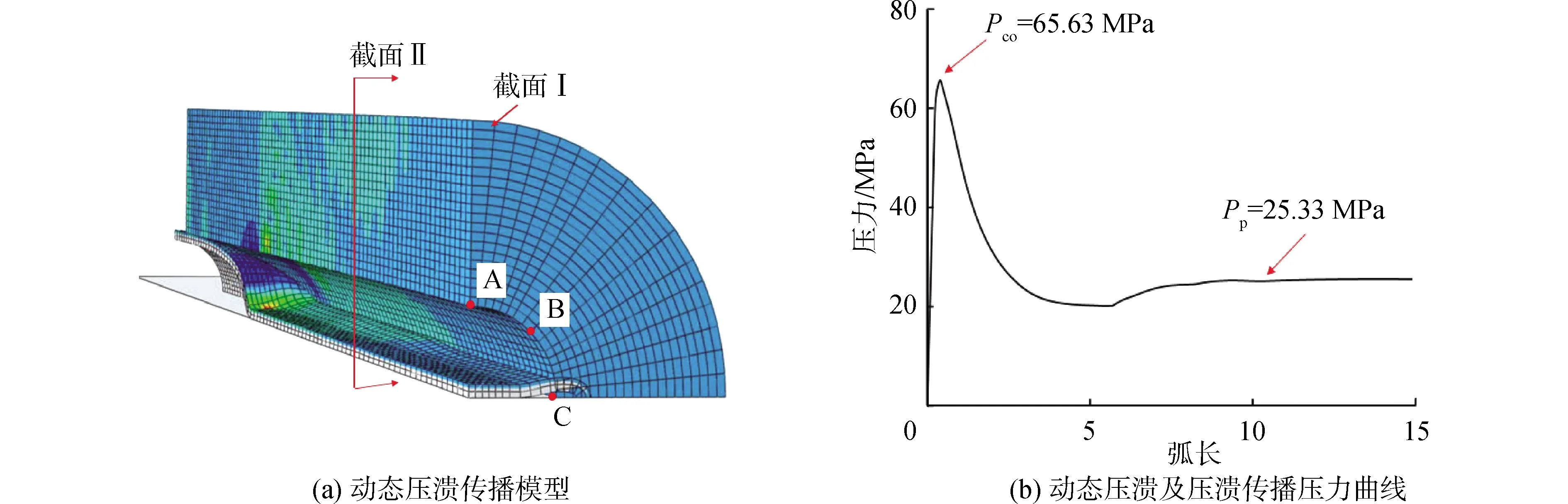
图5 管道动态压溃数值模型

图6为工况4条件下截面I上A、B和C这3个点压力脉冲的变化规律。由图6可知，在管道压溃变形初始时刻，A、B和C这3个点处产生负压力脉冲，该压力脉冲峰值大小近似等于管道压溃压力。随后，管道内壁面与刚性面接触，管道周围流体介质与管道外壁面发生碰撞，进而激发数倍于压溃压力(65.63 MPa)的正压力脉冲，其中，A点处的压力脉冲峰值为341 MPa，B和C点处的压力脉冲峰值分别为231 MPa和125 MPa。压溃发生初始时刻，压力脉冲沿管道周向分布不均匀，垂直于压溃变形方向的压力脉冲峰值最大(见图6中A点)，平行于压溃变形方向的压力脉冲峰值最小(见图6中C点)。压溃发生t=1 ms后，A、B和C这3个点处的压力脉冲显著降低，且分布规律趋于一致。

图6 压溃界面(截面I)处压力脉冲分布规律(工况4)

图7和图8为4种不同工况条件下，截面I和II处垂直于管道压溃变形在近壁面处、距离管道外壁面0.25D和0.5D距离处压力脉冲的演化规律。工况1，工况2，工况3和工况4条件下，管道的压溃压力分别为18.38、29.78、41.79、65.63 MPa，截面I上压溃瞬间激发的最大压力脉冲峰值(近壁面处)分别为125、157、300、341 MPa。

图7 截面I处压力脉冲分布

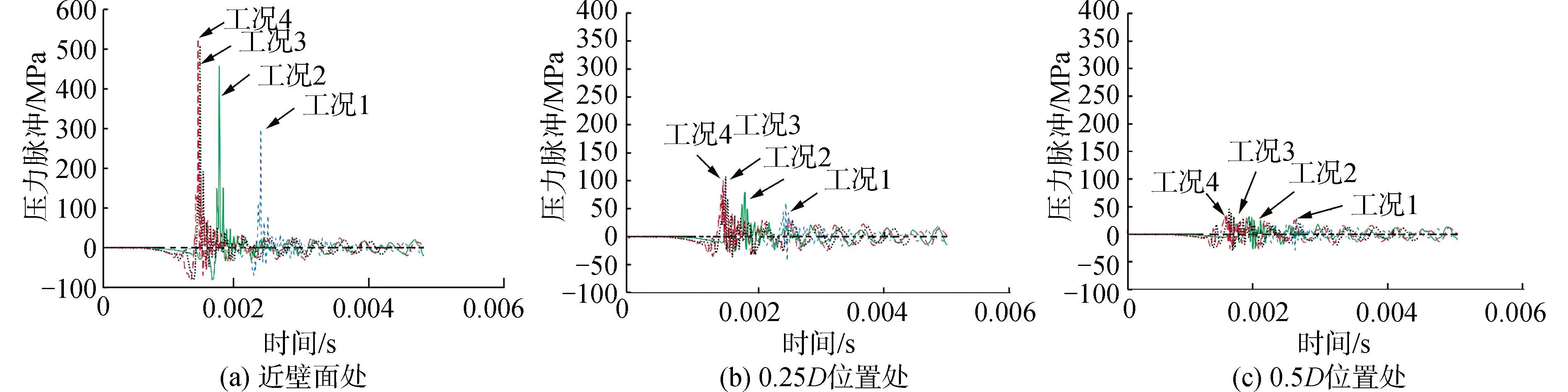
图8 截面II处压力脉冲分布

由此可知，管道压溃激发的压力脉冲峰值与管道压溃压力的大小有关。管道压溃压力越大，其压溃瞬间激发的压力脉冲峰值越大。近壁面处压力脉冲峰值(见图7(a))高于距离管道壁面0.25D和0.5D的处压力脉冲峰值(见图7(b)和(c))。随后，压力脉冲逐渐衰减。对比图7和图8中截面I和II处不同位置处压力脉冲的变化规律可知，压力脉冲随着压溃变形的传播，沿轴向方向传播。

2.2.2L/D=20时压力脉冲变化规律

图9表示L/D=20条件下海底管道的压溃变形和压力脉冲变化的情况。由图9可知，该海底管道在静水压力下发生翻转型压溃传播现象。初始压溃位置处，垂直于压溃变形方向上P1点的压力脉冲峰值最大，约为200 MPa；平行于压溃变形方向的P2点的压力脉冲峰值相对较小，约为70 MPa；随着压溃变形沿着轴线方向的传播，P1和P2点处的压力脉冲逐渐衰减。当压溃变形传递至P3和P4点所在的截面时，压溃变形发生90°变化。此时，位于垂直压溃变形方向上P4点的压力脉冲峰值最大，约为260 MPa。平行于压溃变形方向上P3点的压力脉冲峰值相对较小，约为50 MPa。由图9可知，压溃变形发生90°变化的同时，管道近壁面处的压力脉冲峰值发生的位置发生同样的变化。随着压溃变形沿轴向方向的传播，P3和P4点处的压力脉冲随之衰减，直至压溃变形再次出现90°变化，新的压力脉冲峰值在P5和P6所在的截面出现。压溃脉冲随压溃变形的90°交替变化而变化，直至压溃变形由止屈器等止屈装置阻止。