基于模糊评价的风电场有功功率分配算法研究

王治国，杨印

（西安德纳检验检测有限公司，陕西 西安 710000）

0 引言

当前经济发展速度加快，化石能源日益短缺，加上化工生产造成严重的环境污染，急需寻找新型能源进行替代。风能作为可再生的清洁能源得到广泛应用，在电网中的比重逐渐增加，有效功率输出波动频繁，给电网安全性与稳定性造成不良的影响。因此，当前工程多采用模糊评价模式对风电场功率进行科学分配，对机组载荷、频繁启停等因素综合考虑，确保风电场的安全稳定运行。

1 机组功率调节能力模糊评价

对于风电场功率分配来说，快速准确的评价功率调节率属于关键内容。在风电场机组中，因受到生产与安装误差影响，导致数学模型不尽相同，加上长期使用导致叶片变形、材料老化等，使数学模型参数出现变化，增加功率评价误差。为了节约风电场维修成本，应结合机组运行状态合理分配功率，即优先调度状态良好的机组，减少状态不良机组的调度。当风速为切出风速时，可适当降低机组功率给定，避免叶片载荷增加；当为切入风速时，机组为启动状态，无需进行调度，避免并网接触器重复闭合。为了使每台机组的功率调节能力充分发挥出来，一些具有较强调节力的机组应承担更多的发电任务。根据机组动力学特点，采用模糊评价法对机组调节能力进行测评。

机组限功率运行模糊集包括变桨限功率运行（B）、联合限功率运行（WB）、变速限功率运行（W）三种。因机组功率在调节阶段运行稳定性受到限制，对于单一机组来说，可开展限功率控制实验，当B运行中，风速较小；当WB运行中，风速较大。因此，可将运行对应风速范围分成低速、中速与高速，隶属度由变速机构运行程度而定。调节能力可分为上升与下降两种，二者具有互补性。在B状态运行中，转速始终处于额定转速内，机组转速、最优转速的差异较大，升功率调节力越强，说明隶属度数值越高。当风速为4m/s时，在第i台机组运行中，当转速为每秒1.5rad时，达到最佳值。在功率调节力评价中，不但与风速相关，还关系到转速与桨距角等指标。为了提高功率分配合理性，应对上述指标综合分析，可通过改变桨距角或转速的方式进行功率调节，提高响应速度。但如若变桨系统的操作过于频繁，则会使机组的载荷提升，使转速调节功率被改变，响应速度减慢，但载荷值会由此减小。假设某风速状态下，桨距角用β表示，机组运行的最佳转速为w，与额定转速W相比较低，输出功率用L表示。可通过调整转速的方式，使机组输出功率的最大值、最小值变化。以升功率为例，可采用变速变桨的方式，将给定功率控制在合理范围内；也可通过主动改变转速的方式，对变桨功率进行调节[1]。

2 基于功率调节的风电场功率分配措施

2.1 分配技术基础

以永磁同步风电机组为力，有功功率分配框图如下图1所示。由功率控制器对各台机组风速与实际功率进行采集，风速为VW，1到VW，N，实际功率输出为P1到PN，采用功率控制分配法，分别为每个机组配置一个给定功率，即Pset1到PsetN，最后使风电场中各台机组输出功率的总值与调度给定功率相同，其中前者用Psum表示，后者用Psumset表示。

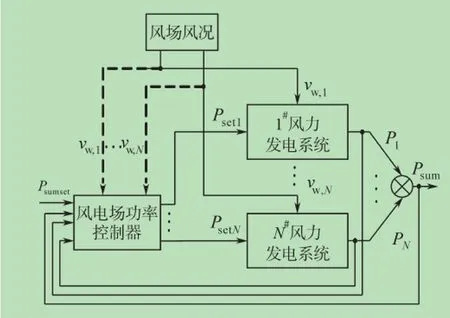
图1 风电场有功功率分配图

2.2 模糊控制流程

根据模糊控制器结构、推理规则、隶属度函数等创建模糊控制算办法，在对有功功率波动有效控制的同时，对风电功率进行平抑，具体流程如下：

第一步：对各参数变量进行初始化，明确电容器、电池运行范围、采样时间、风场容量、并网有功功率要求等，确保N时段内的有功功率波动处于△P之内；

第二步：在电容器与电池常规运行区间，制定隶属度函数、控制规则表，对t时段风电功率与t-N时段功率的最大波动率进行计算；

第三步：在当前电池能量状态下，以模糊控制规则为依据，输出比例系数，并计算出储能出力功率与并网分量值。在当前电容器能量状态下，根据控制规则，计算出电池与电容器的真实输出功率，并对二者的SOE情况进行估算；

第四步：在上述流程完毕后，获得特定时段内并网值、储能信号值与SOE变化曲线[2]。

2.3 升降分配算法

首先，确定各个风电机组所在的调节区，采集机组现行功率、变速功率的升降调节能力；其次，对功率调节区域内机组实时输出功率的综合进行计算，并与给定功率调节区的机组功率相一致；最后，将两组区域的总给定功率相减，判断机组功率需要提升或者下降。在升功率分配中，根据机组WB控制策略，事先按照变转速上升措施进行分配，如若功率调节Ⅰ区与Ⅱ区功率变化情况超出变转速升功率范围，则会受到变桨距角功率增加的影响，使机组整体的升分配能力增强。对变速功率上升能力区间P进行计算时，P为两个区间内机组变转速功率提升力的总和。在降功率分配中，按照变转速下降措施进行分配，如若功率调节Ⅰ区与Ⅱ区功率变化情况低于变转速升功率范围，则会受到变桨距角功率降低的影响，使机组整体的降分配能力降低。对变速功率下降能力区间P进行计算时，P为两个区间内机组变转速功率下降力的总和。在机组能力调节基础上，风电场有功功率的分配措施如下：一是采集场内全部运行机组转速、风速与桨距角信息，依靠以往经验或者查询表，获取现有机组转速最大值与最优值；二是采用机组调节力模糊评价法，结合机组运行状态计算出每台机组升功率调节力，则降功率调节力为前者的模糊补集；三是根据场内有功功率输出与电网调度指令的差值，计算有功功率的偏差，如若偏差超过0，则对场内全部机组进行升功率分配，反之则对全体机组进行降功率分配，为每台机组发布有功功率的给定指令。

3 仿真分析

3.1 基本参数

该风力机组的主要参数为：空气密度1.251kg/m3，桨叶半径为2.5m，额定风速为13.5m/s，风轮额定转速为3.5rad/s，桨距角范围在0～27°之间、变桨系统时间为5min，发电机额定功率为1.3MW。为检验算法的准确性，以10台风电机组为对象，根据某地风电场以往的风速数据，绘制机组1min内的曲线图，发现1～10号机组的风速均值依次提升。

3.2 仿真结果

假设初始桨距角度为0，转速为每秒1rad，有功功率调度指令为5MW。在风速权重下进行分配，计算公式为：

式中，P1代表的是风速权重分配功率；vi代表的是第i台风电机组的总功率。将其与按照调节力权重分配算法相比，有功功率输出曲线与偏差曲线对比明显。采用调节力权重分配的输出效果可使电网功率配置需求得到满足，且场内功率波动值较小，根据功率平滑度定义，有功功率平滑度计算公式为：

式中，Pl代表的是有功功率平滑度；d代表的是功率波动值；dt代表的是功率标准值。将实际值代入公式后可知，按照风速权重计算出的平滑度为68.362，根据调节力权重计算的平滑度为21.584。根据平滑度指标可知，后一种算法的功率分配与输出效果优于前一种。将两种算法的机组转速变动情况对比可知，二者的变化趋势大致相同，但按照调节力权重分配的转速平滑度更高，这意味着该算法的应用可使轴系载荷有效降低，使发电机的效率与寿命得到显著提升。采用上述两种方式进行功率分配，10台机组桨距角曲线不尽相同，以βi作为桨距角，在t时间内角度的最大值可用公式表示为：

式中，βi代表的是第i台机组的桨距角；t代表的是时间段。将真实值代入公式后，可得出按照风速权重算法分配的桨距角为11173.24°，按照调节力权重分配算法的行程为239.55°。根据两幅桨距角曲线图可知，10号机组的风速达到最大值，按照调节力得出的角幅度为13°，而按照风速得出的角幅度为8°，且角幅度与叶片载荷具有反比关系。采用按照调节力权重分配的方式，机组整体桨距角的动作幅度相对较低，可使机组载荷显著降低，延长机组变桨系统寿命。根据调度中心以往调度指令可知，风电场中的有功指令位于3～6MW之间，内部机组桨距角的初始值与转速无变化，仍分别为0和1rad/s，根据机组风速曲线可知，两种功率分配模式下的算法误差较大，且按照调节力分配功率的算法与电网调度指令的控制要求更加贴近，有功功率的输出更为平滑，且桨距角的行程减少[3-5]。

4 结语

综上所述，风电机组作为风力发电的核心设备，当期发生故障时会为人们生产生活带来诸多不便。对此，本文根据机组能力提出一种新的有功功率分配算法，以机组状态信息对依据评价功率调节能力。最后开展仿真分析，对10太机组的有功功率进行分配。根据结果可知，此种方式的效果优于按照风速权重分配，可充分满足电网调度要求。