竖井消能工折板压强及脉动特性分析*

杨 乾，杨庆华

(西南交通大学 土木工程学院，四川 成都 610031)

0 引言

2013年12月，我国首次提出“海绵城市”概念[1]，深隧排水系统已成为大城市解决老城区雨洪灾害及溢流污染问题主要手段[2]。竖井消能工为深隧排水系统重要组成部分，主要负责浅层来流输送与消能，主要包括跌落式、旋流式、螺旋式和折板式4种结构类型，折板式竖井消能工适用性强、消能效果显著，被广泛应用于深隧排水系统[3-7]。

目前，关于折板式竖井消能工的研究主要集中在水力学特性与结构优化[8-11]方面：Margevicius等[12]通过量化和改善折板式竖井水力特性，实现设计流量下最大限度减少主隧道内空气量，保证折板在可承受动水压力范围;Odgaard等[13]对折板式竖井内泄流及水气交换过程进行研究，得到竖井设计约束条件，并推导出折板式竖井关键结构参数理论设计方法；王斌等[14]考虑竖井稳定消能边界条件，建立满足消能条件的折板式竖井最大过流能力关系式，并通过实例验证设计流量；杨乾等[15]通过物理试验与数值模拟，研究折板式竖井湍流耗散特性，建立折板消能计算模型。

折板作为竖井消能工主要受力构件，泄流过程承受来流复杂水动力荷载，设计不当容易使折板产生共振，导致结构发生破坏。本文通过水力模型试验，对不同体型竖井消能工折板壁面压强及脉动特性进行研究，分析不同折板因素对脉动特性影响，为折板式竖井结构设计与安全性评价提供理论参考。

1 模型装置与试验方案

本文以广州市东濠涌深隧工程东风路竖井结构为研究对象。竖井消能工由进水管、竖井井身和出水管3部分组成，竖井直径16 m，埋深38.6 m，最大设计入流量31 m3/s。竖井井身被中隔板分割为湿区和干区2个区域：湿区交错布置等间距扇形折板，主要承担浅层管网来流输送与消能；干区用于机械设备吊装与外部气体交换。折板边缘宽8 m，倾角0°，折板间距3.7 m，通气孔直径1 m。水力模型依据弗劳德相似准则、原型尺寸及试验场地条件，设计长度比尺λl取40，竖井模型直径0.400 m，高度2.400 m，进水管与出水管直径为0.10 m，折板边缘宽度w=0.200 m，折板间距d=0.080，0.097，0.123 m，折板倾角θ分别为 0°，10°，20°，不同折板间距和倾角组合成9种竖井体型。

试验装置如图1所示。试验采用循环水系统，由高位水箱供水，进水管上游阀门控制竖井入流量，利用电磁流量计确定流量大小，试验可提供最大入流量15 L/s。为研究不同位置折板脉动压力，在竖井内选择上中下3处压力测点，分别标记A、B、C，3处测点距井底高度分别为h1、h2和h3，第1层折板和最后1层折板距井底高度分别为h0、h4，不同折板间距对应不同位置折板高度，试验参数见表1。

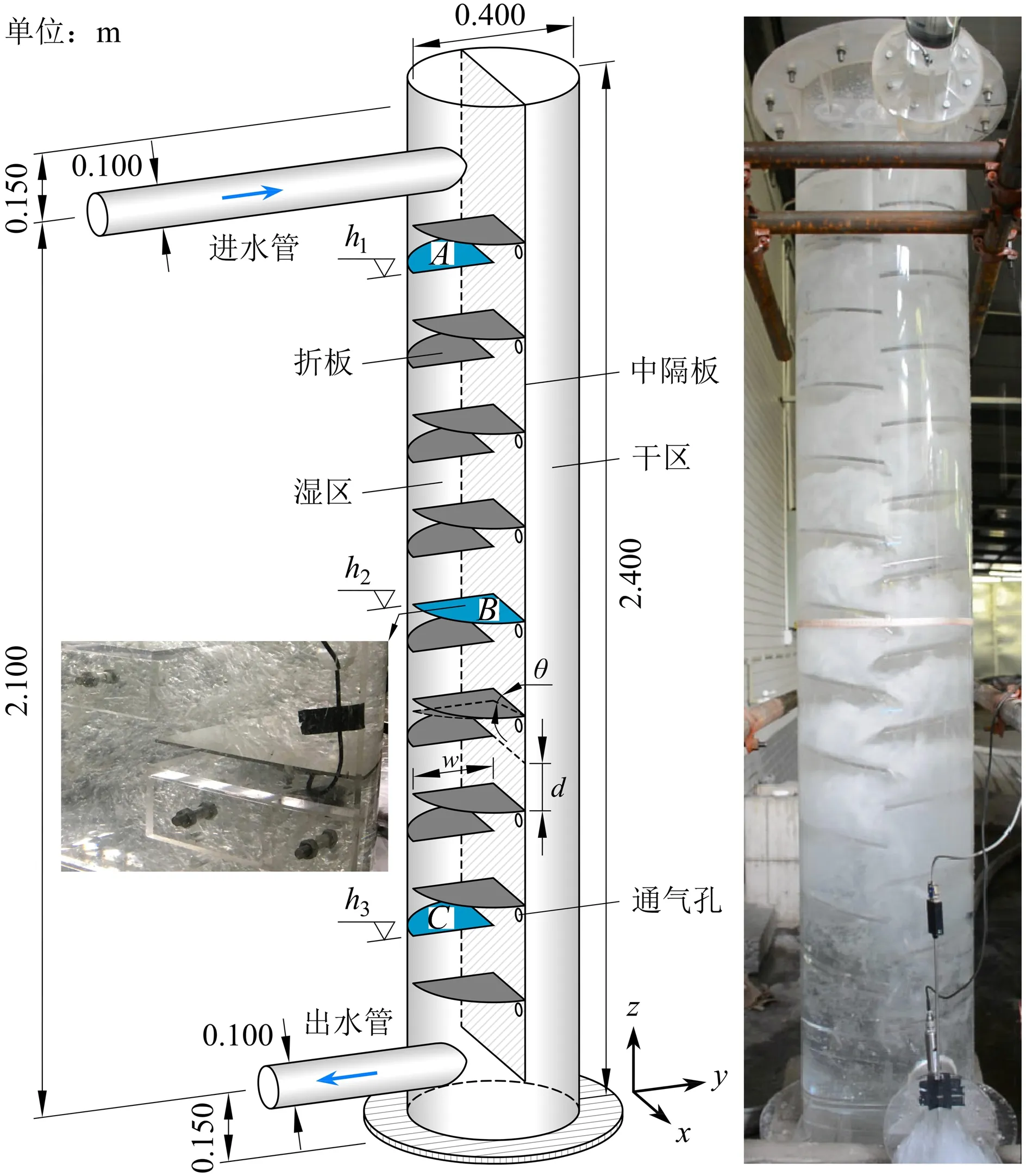
图1 试验装置

试验采用JHBM-H3压力传感器采集折板上脉动压力，传感器承压面与折板尺寸一致，量程0～500 N，精度±0.2% FS，采集频率50 Hz。入流量与脉动压力数据通过SDA1000-SW-V02可视化数据采集系统实现同步监测和采集，为避免零飘影响，试验前对压力传感器归零。折板压强为试验测得脉动压力与传感器承压板面积比值，下文所有物理量均为模型值。试验入流状态为恒定流和非恒定流：恒定流无量纲单宽流量q*为0.075～0.250，见表1，待入流量稳定10 s后开始数据采集，每组采样时长60 s，样本容量3 000个；试验采用非恒定流时，将蓄满水的水箱快速打开，入流量由0增大至10.7 L/s后逐渐减小，采样时长200 s，样本容量10 000个，数据分析截断频率25 Hz。恒定流状态下折板上水流脉动为平稳随机过程，可采用数理统计分析法与频谱分析法研究[16]。

表1 试验参数

2 恒定流条件下折板压强

2.1 时均压强分布规律

泄流过程中，竖井消能工为典型湍流运动，折板上任意时刻瞬时压强pi如式(1)所示：

pi=[p]+p′

(1)

式中：[p]为平均压强，Pa；p′为脉动压强，Pa。恒定流条件下，折板式竖井消能工泄流过程视为时间平稳随机过程，采用时均压强代替恒定流条件下折板上平均压强。

根据表1，在不同恒定流量条件下对9种体型竖井开展8组水力模型试验，当d/w=0.401，θ=0°时，测点A、B、C在不同单宽流量下瞬时压强时程曲线如图2所示。由图2可知，恒定流条件下折板压强在时均压强附近上下波动，随入流量增大，折板时均压强与瞬时压强振幅逐渐增大；由图2(c)可知，q*>0.2瞬时压强振幅逐渐减小，这是因为入流量增大导致测点C折板淹没，作用在传感器上脉动荷载受水垫层缓冲作用被削弱，脉动压强振幅减小。相同恒定流条件下，不同测点时均压强为测点A大于B和C，测点B和C时均压强基本相同，这是由于刚进入竖井的水流具有较大动能和势能，在测点A处水流未被及时消杀，随水流逐层跌落，能量被逐渐耗散，导致测点B和C时均压强差异较小。

图2 恒定流条件下典型测点瞬时压强时程

不同折板间距和倾角时均压强如图3～4所示。由图3可知，当折板倾角一定时，测点A时均压强随折板间距增大而减小，介于0.2～1.5 kPa；测点B和C时均压强在不同折板间距下无明显变化规律，且2者时均压强差异较小，介于0.1～0.7 kPa。由图4可知，当折板间距一定时，不同折板时均压强随折板倾角增大而减小，测点A、B、C同上述变化规律一致，时均压强介于0.03～1.4 kPa之间，这是由于随折板倾角增大，水流无法在折板长时间停留，沿折板边缘顺势跌落，折板水垫层厚度减小，作用在折板上静水压力相应减小。根据时均压强分布规律，竖井上层折板在泄流过程中受较大水动力荷载，时均压强值为中下层折板1.5～3倍。因此，应加强竖井上层折板以提高结构安全性。

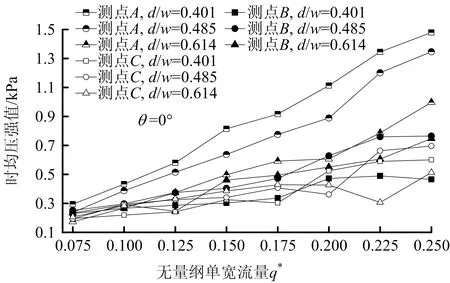
图3 不同折板间距时均压强值

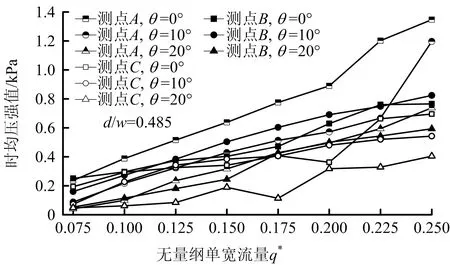
图4 不同折板倾角时均压强值

2.2 折板压强脉动特性

2.2.1 脉动压强概率密度分析

脉动压强幅值通过概率密度分布函数体现。采用偏态系数和峰态系数表征与标准正态偏离程度，如式(2)～(3)所示：

(2)

(3)

式中：N为样本容量；CS为偏态系数，表征分布函数对称性，CS=0表示对称分布；CE为峰态系数，表征峰值高低与标准正态偏离程度，CE=3为标准正态分布；σ为均方根值，表征压强脉动剧烈强度，如式(4)所示：

(4)

当d/w=0.485，θ=0°时，不同流量条件下测点A、B、C脉动压强偏态系数与峰态系数见表2。由表2可知，测点A偏态系数CS介于-0.447～0.008，峰态系数CE介于2.731～4.679；测点B偏态系数CS介于-0.718～0.039，峰态系数CE介于2.443～3.327；测点C偏态系数CS介于-1.142～0.32，峰态系数CE介于2.47～4.379。3处测点实测脉动压强概率密度基本符合正态分布，且具有一定对称性，其中测点A和B脉动压强概率密度分布如图5所示。测点A均方根σ随入流量q*增大而增大，说明折板脉动压强强度与入流量呈正相关性；测点B和C均方根值σ随入流量增大呈先增大后减小变化规律，原因是随入流量增大，作用在折板上动荷载和静荷载同时增大，使脉动压强增大，当入流量增大至临界值，折板出现较厚水垫层，使上层跌落水流得到缓冲，削弱折板上动荷载作用，脉动压强强度减小。

表2 不同测点脉动压强偏态系数与峰态系数

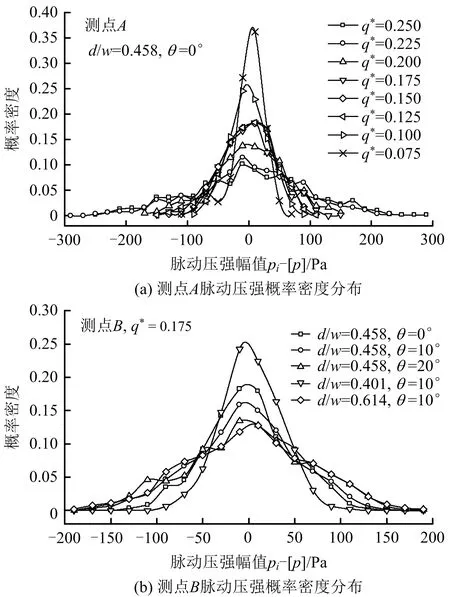
图5 测点A和B脉动压强概率密度分布

由图5(a)可知，测点A折板脉动压强概率密度分布随入流量减小,脉动压强幅值范围变小，概率密度分布曲线越瘦高。由图5(b)可知，当折板间距d/w一定时，随折板倾角增大，测点B压强幅值增大，概率密度曲线越矮胖，这是由于折板倾角变大，水垫层厚度减小，跌落水流直接撞击折板，使增脉动压强幅值变大；当折板倾角θ一定时，脉动压强概率密度分布随折板间距增大，幅值范围变大，水流在上层折板重力势能增大，跌落至下层折板时转化为动能比例提高。脉动压强由紊流中各层质点互相掺混产生，动能越大，水流掺混程度越高，脉动压强幅值越大。

对于标准正态分布，区间(-3σ,+3σ)样本数占总量99.73%，根据图5中所有工况概率密度分布，将取样范围扩大至(-5σ,+5σ)，样本数占总量99.99%。因此，按照5倍的σ计算最小压强相对安全。

2.2.2 脉动压强频谱特性分析

不同工况条件下，脉动压强具有不同频谱特性，当脉动压强优势频率与折板自振频率非常接近时产生共振现象，严重威胁竖井消能工结构安全。采用功率谱密度(Power Spectral Density，PSD)表征脉动压强频域分布，即将随机序列x(n)进行离散傅立叶变换，得到频域内对应点脉动压强频谱，如式(5)所示：

(5)

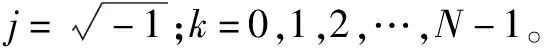
对于有限长序列随机信号，通过快速傅立叶变换(Fast Fourier Transform，FFT)计算功率谱密度，不同工况下典型测点归一化功率谱密度分布如图6所示。由图6可知，不同入流量、折板间距、倾角及测点功率谱密度不同，且具有一定随机性，优势频段主要集中在0～2.5 Hz之间，低频特性明显。通过对比入流量、折板间距和倾角对频谱特性影响发现，功率谱密度随入流量增大而增大，主频0.27 Hz；当折板间距逐渐增大，功率谱密度随之增大，并向频段0.5～1.5 Hz集中，当d/w=0.614时，主频为0.8 Hz；当折板倾角θ=0°时，功率谱密度主要分布在0～2 Hz，主频1.3 Hz；当θ=10°，20°时，功率谱密度向低频段转换，2者主频分别为0.1，0.2 Hz。

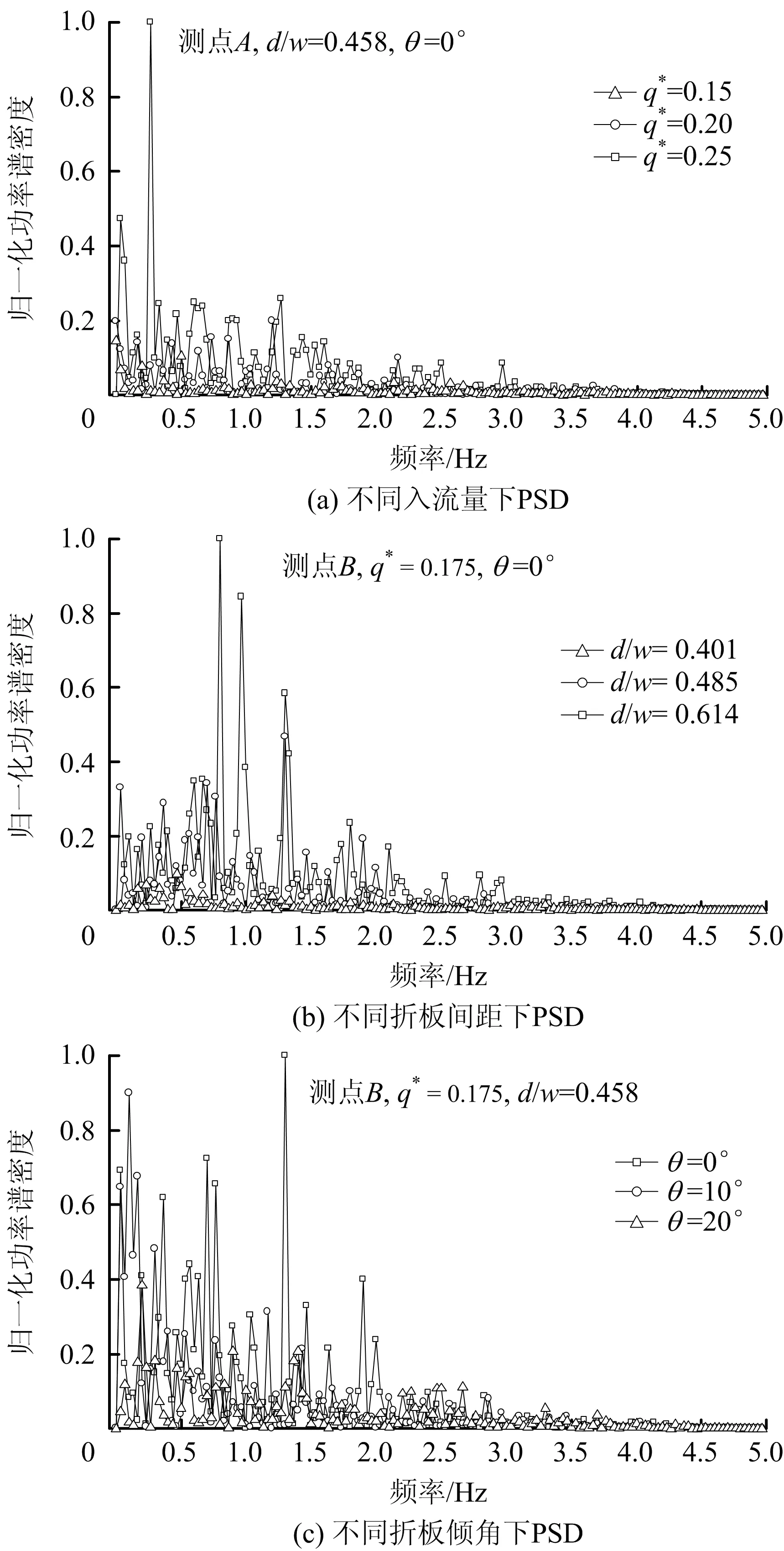
图6 不同工况下典型测点的功率谱密度

实际工程中采用有限元模型研究不同工况下折板自振特性，通过与试验监测数据对比，防止竖井消能工最低频率介于脉动压强优势频率范围内，避免折板与脉动水流共振。

3 非恒定流条件下折板压强

3.1 瞬时压强分布规律

实际工程中，折板式竖井消能工泄流过程以非恒定流为主，入流量随降雨强度与调度方式不同而变化。非恒定流条件下，不同测点瞬时压强随入流量变化时程曲线如图7所示。由图7可知，折板瞬时压强随入流量产生较大波动，脉动压强属典型非平稳随机过程。瞬时压强与入流量变化趋势基本相同，不同测点间瞬时压强变化规律有所差异。由图7(a)可知，在0～100 s内，不同测点瞬时压强piA>piB>piC，说明随水流逐级跌落，水体携带能量不断耗散，作用在折板上压强随之减小；在100～200 s内，3个测点瞬时压强变化基本一致，但随入流量减小，折板瞬时压强脉动强度与脉动幅逐渐减小；由图7(b)可知，在0～100 s内，测点C瞬时压强呈局部稳定或下降趋势，主要原因是入流量过大，竖井底部产生积水，将测点C折板淹没，作用在折板上动水压力被水垫层吸收耗散，瞬时压强脉动强度和脉动幅值减小，结果与图2(c)恒定流条件下测点C瞬时压强变化规律相同。

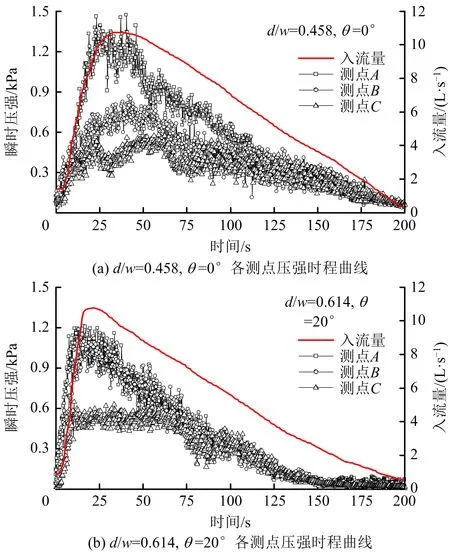
图7 非恒定流条件下典型测点瞬时压强时程曲线

不同折板间距和倾角条件下测点B瞬时压强时程曲线如图8所示。由图8可知，当折板倾角θ一定时，随折板间距d/w增大，作用在折板上瞬时压强增大，相同时刻折板间距较大的瞬时压强脉动强度和脉动幅值偏大。原因是折板间距较大，使跌落水流作用在折板动荷载变大，水流湍流强度增强，折板脉动压强波动更加剧烈，波动幅值变大，折板间距d/w由0.401增至0.614，对应最大瞬时压强依次为0.709，0.914，1.291 kPa。当折板间距d/w一定时，随折板倾角θ增大，作用在折板瞬时压强减小。相同时刻折板倾角越大，折板瞬时压强脉动强度与脉动幅值越小，原因是折板倾角增大，导致水流无法在折板长时间停留，水垫层厚度减小，作用在折板上静水压力降低，折板瞬时压强减小，折板倾角θ由0°增大至20°，对应最大瞬时压强依次为1.469，0.914，0.711 kPa。

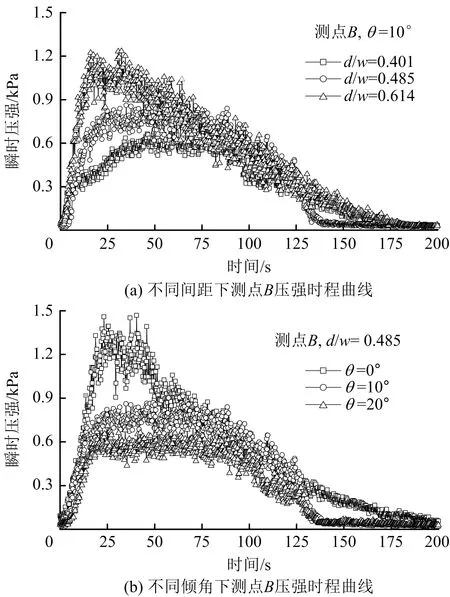
图8 不同折板间距和倾角下典型测点瞬时压强时程曲线

3.2 折板压强脉动特性

由图7～8可知，非恒定流条件下折板上水流过程属典型时域非平稳随机过程，时均压强随时间不断变化，对于非平稳随机过程频谱特性，可采用功率谱密度表示[17]。计算前对瞬时压强进行平滑处理，获取折板瞬时压强时变平均值。以d/w=0.614，θ=20°竖井为例，分别采用S-G(Savitzky-Golay)滤波法、FFT滤波法和Loess滤波法对测点B非平稳瞬时压强进行滤波处理，得到滤波后脉动压强。在非恒定流条件下，折板脉动压强振幅快速增大，稳定一段时间后，随入流量减小波动变小，脉动幅值介于-0.2～0.2 kPa，3种滤波方法得到的脉动压强变化趋势基本相同，考虑S-G滤波法原理简单，计算效率高等优势，本文采用S-G滤波法获取脉动压强。

对于非平稳随机过程脉动压强，通过短时傅里叶变换(short-time Fourier transform，STFT)获取时变功率谱密度，如式(6)所示：

(6)

式中：x(n)为时域离散随机序列；g(m)为具有一定时间长度的窗函数；ω为连续频率变量。

当d/w=0.614，θ=20°时，典型测点A、B、C归一化功率谱密度如图9所示。由图9可知，非恒定流条件下折板脉动压强功率谱密度在频段分布上与恒定流不同，并且随时间不断变化。通过对比可知，测点A优势频段为0～4 Hz，测点B和C优势频段分别为0～3 Hz，0～2 Hz，表明随水流不断跌落，作用在折板上非平稳脉动压强逐渐向低频段转换，3个测点主频均为0.45 Hz。此外，测点B低频分布时域为0～120 s，相对较宽，测点A低频分布时域相对较窄，在0～80 s之间，测点C低频分布时域范围相比测点A和B更为集中。对所有测试结果计算，得到非恒定流条件下各测点优势频段均集中于0～4 Hz，低频特性显著，但主频和优势频段在时域上分布因体型和测点位置不同而不同。

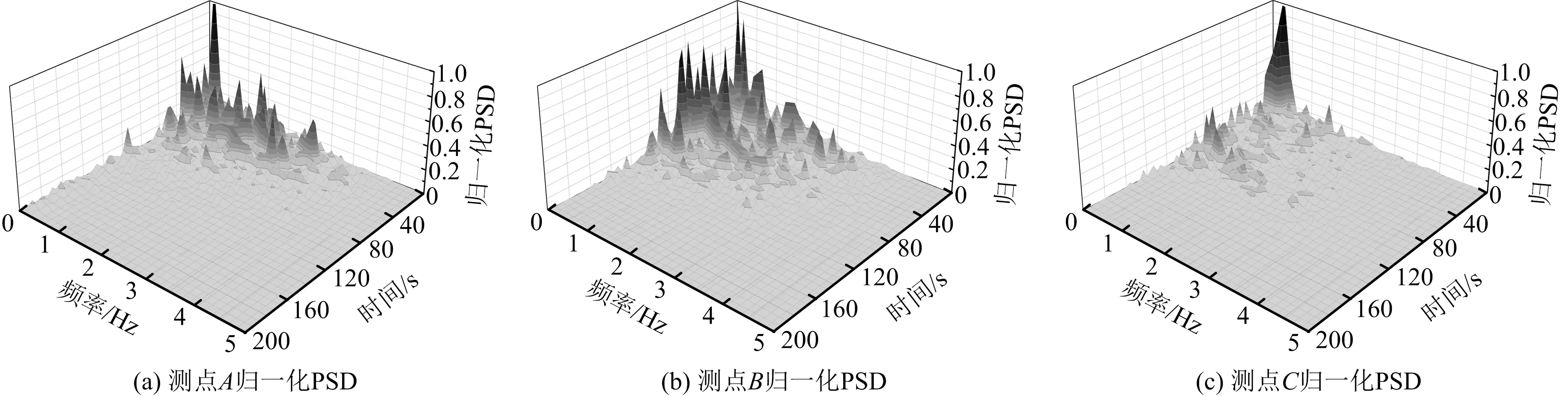
图9 非平稳脉动压强归一化功率谱密度

4 结论

1)恒定流条件下，不同位置折板时均压强分布规律不同，相比中层和下层折板，上层折板承受水动力荷载更大，时均压强为中下层折板1.5～3倍。

2)恒定流条件下，折板脉动压强概率密度基本符合正态分布，脉动幅值随入流量和折板间距增大而增大，随折板倾角增大而减小；平稳随机脉动压强功率谱密度优势频段主要集中在0～2.5 Hz，功率谱密度随折板倾角增大向较低频段转换。

3)非恒定流条件下，不同位置折板瞬时压强由上而下依次减小，脉动压强强度和振幅先快速增大，稳定一段时间后随入流量减小而逐渐减弱，脉动幅值介于-0.2～0.2 kPa。

4)非恒定流条件下，折板脉动压强功率谱密度优势频段集中于0～4 Hz，且随折板位置自上而下功率谱密度向更低频段转换，相比较于上层和下层折板，中层折板低频分布时域相对较宽。