随机载荷下基于Kriging模型的车辆十字轴结构优化*

童林军，曾 威

(1.佛山职业技术学院汽车工程学院，广东 佛山 528137；2.西安石油大学机械工程学院，陕西 西安 710065)

十字轴作为车辆传动系统的重要部件，在使用过程中频繁受到冲击载荷的作用，若其强度不能达到使用要求，会导致轴颈断裂，影响车辆的正常使用。为了提高十字轴结构强度，田辉等[1]采用有限元方法对某型车辆十字轴的结构强度进行了分析，并通过分析结果优化了十字轴结构，提高了十字轴的整体强度。陈科等[2]使用变曲率曲线作为轴根过渡曲线，降低了十字轴轴根位置应力集中的问题。付胡代等[3]使用ANSYS软件分析了十字轴工况下的应力分布情况，并使用试验设计与重复有限元分析的方式，对应力较大的轴根圆弧曲线进行了优化，提高了十字轴的强度。

上述工作通过分析十字轴工况下的应力分布情况，并对十字轴的轴根圆弧曲线半径进行了优化，一定程度上提高了十字轴的结构强度，提高了车辆的使用可靠性。但是，在分析过程中均将十字轴载荷作为一个确定值，没有考虑车辆在使用过程中载荷的随机性及其对十字轴轴根圆弧半径设计的影响，不能够保证十字轴结构的最优性。同时，在优化过程中需要重复使用有限元方法分析不同轴根圆弧半径下的结构强度，导致优化成本较高，优化计算求解效率较低。

本文充分考虑车辆十字轴载荷的随机性，将之作为一个随机变量，并使用Kriging方法构建十字轴强度关于轴根圆弧半径的近似模型，建立十字轴结构优化数学模型，采用遗传算法对十字轴的结构进行优化设计，获得具有全局最优性的十字轴结构。

1 十字轴结构强度随机有限元分析

1.1 某车辆十字轴主要结构参数

以某车辆SWC180型万向联轴器的十字轴为对象，其材料为20CrMnTi，轴根过渡线段使用了单一圆弧曲线，具体的结构尺寸如图1。其中，轴根圆弧曲线半径R=25 mm。根据文献[1-3]的分析，影响十字轴强度的主要参数即为R，因此本文将之作为优化设计变量。

图1 十字轴结构尺寸

1.2 随机载荷的确定

该十字联轴器的公称转矩Mj=12.5 kN·m，使用文献[1]中的计算方法，将十字轴的载荷等效为一作用在轴颈的余弦分布载荷P(α)，具体计算公式如式(1)所示：

(1)

其中，α为任意圆心角，l为作用点到十字轴中心距离，b为分布载荷宽度，r为十字轴颈断面圆半径。

根据1.1节所示十字轴结果尺寸，使用公式(1)，计算得到载荷的最大值Pmax(α)=85.6 MPa。为了考虑十字轴实际载荷的随机性，假设载荷分布服从均值μ=85.6 MPa的高斯分布，变异系数cv=0.05。基于3σ准则，确定轴颈载荷服从截断型高斯分布，其上限、下限分别为72.76 MPa、98.44 MPa。最终，得到该十字轴的随机载荷为：

P～N(85.6，4.282)，p∈[72.76，98.44]

(2)

1.3 随机有限元分析

十字轴材料为20CrMnTi，在有限元软件Abaqus中，设材料弹性模量为209×103MPa，泊松比为0.28。使用4节点Tet单元C3D4对十字轴模型进行离散，获得十字轴的有限元模型。

为了模拟十字轴的实际工况，如图2所示，约束图中横向两轴颈的自由度，并在垂直方向两轴颈添加如式(2)所示的随机载荷。

图2 十字轴边界条件

使用Abaqus的inp文件，编写概率分析文件，使用拉丁超立方抽样方法对式(2)确定的随机载荷进行抽样，并施加在如图2所示的十字轴轴颈上，通过静强度计算，就能够获得不同轴根圆弧曲线半径对应的最大Mises应力σ。例如，当圆弧半径R=25 mm时，随机载荷下十字轴的Mises应力分布如图3所示。

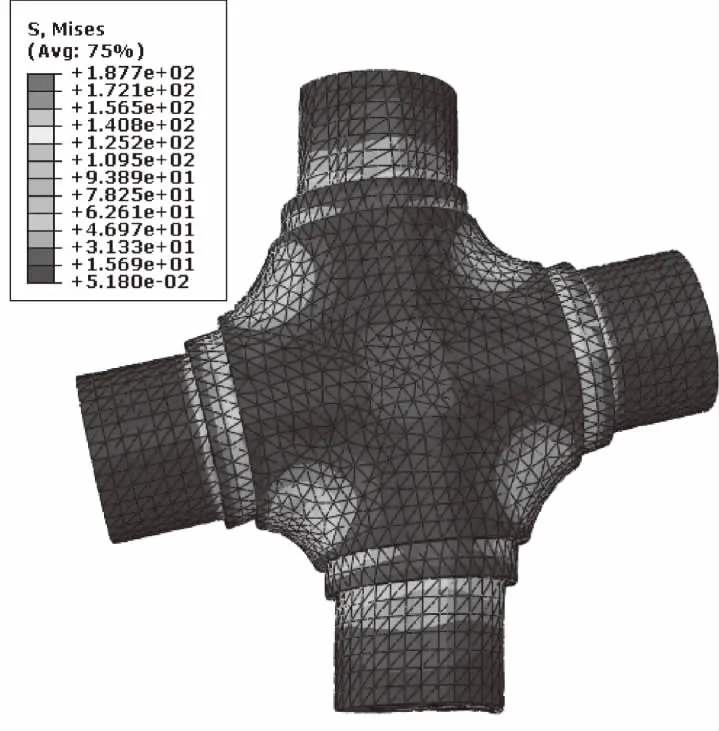
图3 随机载荷计算结果

2 十字轴结构强度Kriging模型

2.1 Kriging模型的基本形式

Kriging模型是一种估计方差最小的无偏估计模型[4]，能够分析样本数据间的相关关系，并以此预测样本的趋势和动态，能较好地拟合十字轴轴根圆弧半径R与响应量σ之间的非线性关系。一个典型的Kriging模型包括回归部分与非参数部分：

(3)

(4)

Z(X)是均值为0，方差为σ2的随机过程，则任意两样本点间的相关关系可以用式(5)描述：

Cov[Z(xi)，Z(xj)]=σ2R[R(xi，xj)]

(5)

其中：σ2是随机过程方差；R是n×n阶的对称正定对角矩阵；R(xi，xj)为任意两个样本点xi与xj的空间相关函数，工程应用中一般用高斯相关函数进行描述：

(6)

(7)

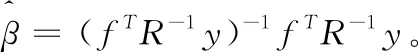
为了获得模型的相关参数θk，可用式(8)所示的最大似然估计方法：

(8)

获得Kriging模型的相关参数θk之后，即可通过式(7)得到预测值，最终构建得到十字轴应力σ的Kriging模型。

2.2 十字轴结构强度Kriging模型的构建

为构建十字轴结构强度Kriging模型，以十字轴轴根圆弧半径R为优化设计变量，以随机载荷作用下十字轴最大Mises应力σ为响应值。Kriging模型的训练样本数量m=3k，其中k=(n+1)(n+2)/2，n为设计变量个数。因为本文设计变量数n=1，因此训练样本点数为9。

以当前圆弧半径R=25 mm为中心，上下浮动50%，确定训练样本的取值区间为R∈[12.5，37.5]。为了保证样本的均匀性，使用拉丁超立方试验设计方法[5]，从变量取值区间中抽样9组设计变量值，使用第2节构建的随机有限元方法，计算不同圆弧半径对应的Mises应力值，并将之作为十字轴Mises应力Kriging模型的训练样本，如表1。

表1 Kriging模型训练样本

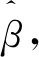
(9)

用式(8)计算得到模型的相关参数θk，得到Mises应力的Kriging模型相关参数θk=0.121。最后，能够计算任意点x与已知样本数据间的相关向量rT，通过式(7)得到响应值，即构建得到Mises接触应力的Kriging模型。

为了检验构建的Kriging模型的预测精度，采用均方根误差[6]作为精度检验指标。由式(7)可得Kriging模型预测点的均方根误差为：

(10)

检验时，在表1中随机选取了5组训练样本数据作为误差检测样本，将之与由Kriging模型拟合得到的Mises应力值进行对比，获得的RMSE值为0.032，表明构建的Kriging模型具有较高的预测精度，能够拟合十字轴Mises应力随机有限元分析结果。

3 基于Kriging模型的十字轴轴根圆弧半径优化

3.1 十字轴轴根圆弧半径优化设计模型

以十字轴轴根圆弧半径R为优化设计变量，以随机载荷作用下十字轴的最大Mises应力σ为响应值，使用构建的Mises应力Kriging模型为目标函数，构建轴根圆弧半径R的优化设计模型：

(11)

式中，σ(R)是构建Mises应力Kriging模型。

3.2 基于多岛遗传算法的轴根圆弧半径寻优

为了获得全局最优的十字轴轴根圆弧半径R，须使用优化算法对式(11)所示的轴根圆弧半径优化模型进行求解。多岛遗传算法[7]能高效率的获得具有全局最优性的优化解，本文使用该算法对轴根圆弧半径进行寻优计算。寻优计算过程如图4所示。

根据图4所示的优化结果，十字轴轴根圆弧半径R的最优值为27.27 mm。为了检验该结果的准确性，将优化后的圆弧半径R代入到随机有限元模型中进行结构强度分析，在相同工况下，得到此时十字轴的Mises接触应力值为150.1 MPa，如图5所示。与原始结构对应的Mises应力值相比，Mises应力值降低了37.6 MPa，验证了本文优化方法的有效性。

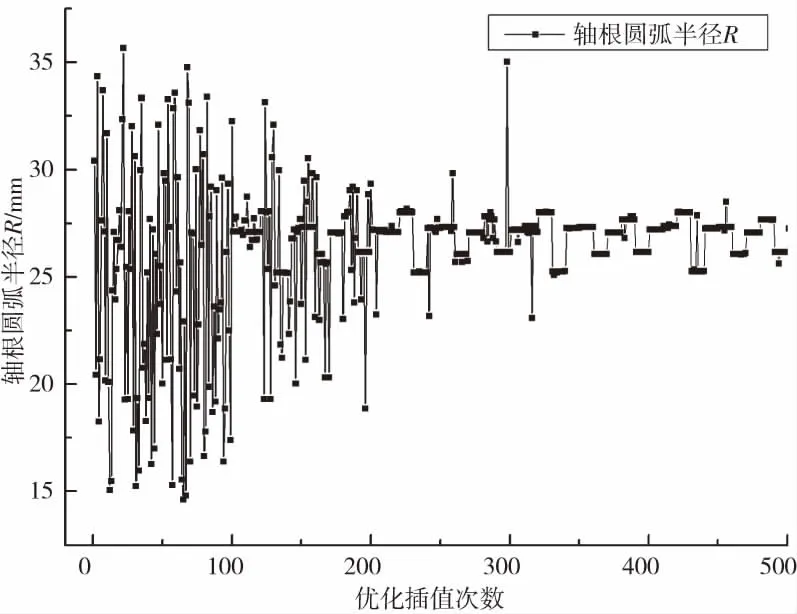
图4 设计参数寻优历程

图5 优化后的Mises应力分布

4 结论

1)以十字轴轴根圆弧半径为设计变量，以车辆十字轴工况条件下的Mises应力为十字轴结构强度衡量指标，构建了十字轴结构强度的Kriging模型，为十字轴结构强度计算提供了高精度的近似模型。

2)构建了以十字轴结构强度Kriging模型为目标函数的轴根圆弧半径的优化模型，并使用多岛遗传算法获得该十字轴轴根圆弧半径的最优值。优化后，工况条件下十字轴Mises应力降低了37.6 MPa，该优化方法得到验证。