基于波速对渗透性反演的富水砂岩注浆效果分析

2021-07-12赵立权胡惠华2姚盛丹3赵延林4

长江科学院院报 2021年7期

陈宾，赵立权，胡惠华2，姚盛丹3，赵延林4，刘通

(1.湘潭大学湖南省岩土力学与工程安全重点实验室，湖南湘潭 411105 ; 2.湖南省交通规划勘察设计院有限公司，长沙 410008; 3.湖南省怀芷高速公路建设开发有限公司，湖南怀化 418000;4.湖南科技大学湖南省煤矿安全开采技术重点实验室，湖南湘潭 411201)

1 研究背景

与黏土层和完整砂岩岩层相比，富水破碎砂岩胶结强度低，砂水分离明显，透水性强，不利于地下施工与基础建设，多采用降水、注浆等方法进行治理[1]。注浆作为一种改善富水岩层力学及抗渗性能的常用手段，其注浆效果对工程质量至关重要。但注浆的隐蔽性导致难以采用直观检测方法对效果进行评价。目前注浆效果评价以岩体完整性、固结度和渗透性等方面为主，常用手段有：钻孔取心、孔内弹性模量检测[2]、室内岩心试验[3]、压水试验、声波检测[4]、电法检测等[5]。但在富水环境下，流水及破碎岩壁对压水试验和钻孔摄像等检测不利，并会使岩体电阻率等电磁参数不稳定，影响电法检测准确率[5]。而以水为耦合剂传递纵波，通过获取纵波在各深度地层的传播特性判断注浆效果的声波检测方法，更适用于富水岩层。国内外学者通过注浆前、后的波速分析，反演获得了注浆前、后岩体完整度、刚度、强度等表征注浆效果的参数变化，如：Kohkichi等[6]基于波速试验，发现初始岩土变形性能与注浆加固效果成正相关；张文举等[7]通过大量工程试验数据，提出波速提高率与原岩体波速的关系，指出可灌性决定最终固结效果；简文彬等[8]在试验的基础上，采用弹性波理论以及修正的Hoek-Brown准则，获得注浆岩体动弹性模量提高率、强度参数提高率与波速提高率间的函数关系。但是利用波速反演岩体渗透性的试验研究仍展开不足。该项研究若与声波测井远探测技术[9]相结合，可检测到距离检测孔数十米范围内岩层的渗透性，实现深度逐点细部检测，突破压水试验只能获取测段平均渗透率以及检测范围的局限。

本文根据Wyllie-Clemenceau波速-孔隙率模型与Kozeny-Carman渗透率方程，推导了富水岩体波速-渗透率理论模型，并结合注浆前、后岩心试样声波检测与渗透试验结果，通过数据拟合，对模型进行了验证与修正。以原位压水试验获取注浆前、后岩层测段的平均渗透性，采用声波测井获取岩层原位波速。将测井波速代入修正模型，计算得到原位检测点各深度岩层渗透率。将测点计算渗透率转换为测段渗透率，与压水试验数据对比，验证了模型在工程应用中的有效性。在建立波速-渗透率关系的基础上，获得计算渗透率，构建了富水砂岩注浆效果评价体系，并针对实际工程项目进行了评价。

2 岩土体波速-渗透率模型研究

2.1 波速-孔隙率模型

经过长期实践与研究，声波测井所得纵波波速与岩土层孔隙率具有一定的相关性。Wyllie等[10]提出理想理论模型，即时间平均公式为

Δt=(1-ø)Δtm+øΔtf。

(1)

式(1)可变换为

(2)

式中:Δt、Δtm、Δtf分别为岩土层、岩土骨架和孔隙流体的声波时差；ø为孔隙率；V、Vm、Vf分别为岩土层、岩土骨架和孔隙流体的纵波波速。其中Δt=1/V、Δtm=1/Vm、Δtf=1/Vf。

上述公式仅适用于孔隙率在20%～30%范围内含泥量较少的地层中。Raymer等[11]基于应用实践数据，提出适用于岩层孔隙率低于37%的经验公式，即

V=Vm(1-ø)2+Vfø 。

(3)

Raiga-Clemenceau等[12]通过大量试验并结合物理模型，得到半理论半经验公式,即

(4)

式中x为岩性指数，与骨架性质和结构相关，由岩体类型确定经验取值范围[13]。该公式对孔隙率<50%的砂岩和石灰岩等适用，但缺乏对流体的计算。

Kamel等[13]对以上研究进行互补整合，同时分析岩性与流体对声波的影响，结合式(2)与式(4)，以砂岩试验为基础，获得Wyllie-Clemenceau公式：

(5)

2.2 孔隙率-渗透率模型

多孔介质常以Kozeny-Carman方程[14-15]表示渗流过程中孔隙率与渗透率之间的关系,即

(6)

式中:k为渗透率；c为Kozeny-Carman常数；S为固体比表面积。

2.3 波速-渗透率模型

由以上研究可知，岩土体的纵波波速V、孔隙率ø、渗透率k三者存在着函数关联性。以孔隙率ø为关联媒介可得到波速-渗透率模型。Jiang等[16]对花岗岩采用高温处理，使内部孔隙变化，发现波速与渗透率存在关系。鉴于花岗岩低孔隙率状况，将Raymer公式(式(3))与Kozeny-Carman方程式(式(6))结合，构造花岗岩波速-渗透率模型为

(7)

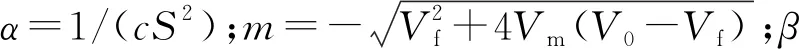
对于花岗岩一类近似各向同性岩体，可采用式(7)通过波速分析干燥状态下岩体的渗透率。而本文研究的富水砂岩岩体破碎，处于水饱和状态，水流方向及流速稳定，并具有承压性。注浆后因浆液扩散充填，原岩物理力学性质改变。构建对应模型时应考虑流体、岩体、砂岩非均质性及注浆效应影响。Wyllie-Clemenceau公式(式(5))的基本假定为声波通过唯一流体与岩体骨架相夹杂的孔隙岩块传播。式(5)中岩性指数x和骨架波速Vm均与岩体性质相关。Kozeny-Carman方程式(式(6))适用于多孔介质单相液体渗流与孔隙率的计算。富水砂岩物理状态满足式(5)基本假定与式(6)的适用条件，以孔隙率为媒介，将式(5)代入式(6)计算，形成富水砂岩波速-渗透率模型，其表达式为

(8)

3 注浆试验及检测

3.1 试验区地质条件

模型的正确性以及在注浆应用上的可靠性需要进行试验验证。工程试验区为湖南怀化的某在建高速立交桥桩基施工现场。场地岩性以红砂岩为主，岩层上层为填土、粉质黏土、淤泥质粉质黏土，厚度约为3.0～9.3 m；其下为第三系泥质粉砂岩，并且夹杂强风化砂岩以及压碎岩，厚度约为12.5～26.1 m；下伏基岩为白垩系含砾砂岩。岩体渗透等级整体为中等透水。上覆黏土层与完整砂岩岩层之间、砂岩岩层与含砾砂岩岩层之间的接触带存在流砂与压碎砂岩，并含有承压水。地形构造整体呈东北向，场地发育断层，其整体走向约213°。

3.2 注浆试验及效果检测

为保证富水地区人工挖孔桩施工安全以及成桩质量，需对桩周预注浆，形成止水帷幕后开挖。试验采用水泥-水玻璃双液注浆，以静压注浆与钢花管注浆相组合。浆液采用PO.32.5普通硅酸盐水泥，以水玻璃为速凝剂，以三乙醇胺和食盐作为早强剂。为防止动水在浆液凝固前将其驱替、融侵，并保证浆液可注性与扩散性，取浆液水灰比为0.8∶1，水玻璃比例为8%，分管汇合注入岩体。

预挖桩长26 m，为确保止水帷幕的效果，设定注浆深度30 m。每桩设置注浆孔两排，均匀布置，共36孔，详见图1。注浆顺序为先进行静压注浆，后进行钢花管注浆，并采取随钻随注、跳孔注浆方式。静压注浆压力控制于0.5～0.8 MPa，钢花管注浆压力控制于0.1～0.5 MPa。

图1 注浆孔布置

为反映不同位置注浆效果，布置1—4号检测孔(图1)，进行钻孔取心，开展声波测井和压水试验等原位检测，对部分岩心开展声波检测、渗透试验等室内试验。1号孔作为注浆前检测孔与注浆孔，其原位试验及室内试验结果代表注浆前岩层物理力学特性。注浆后钻取2—4号孔，进行原位检测和室内试验，其结果代表注浆后岩层物理力学特性。

声波测井采用TH208声波检测仪与单发双收一体式换能器，检测时无套管。换能器与检测仪通过刻度导线连接，导线最小刻度为0.2 m，量程为50 m。检测位置深度为11.2～26.0 m，间隔0.4 m深度进行逐点检测，单孔共38个检测点。

压水试验采取3压力5阶段对岩层渗透率检测，并按钻探深度分段进行。试验的3压力分别为0.1、0.3、0.5 MPa。压水试验按照规程[17]进行，并以规程中的公式计算得到渗透系数与渗透率。深度0～11 m岩层为上覆黏土层，渗透率低，处于承压水层之上，在本次试验中不作为研究对象。

为分析砂岩波速-渗透率关系和注浆影响，取未注浆岩心及注浆岩心进行声波检测和变水头渗透试验。为加强注浆试验的对照性，采用距离最近的1号、2号检测孔内的岩心，作为注浆前、后的研究对象。利用切割工具制成直径61.8 mm、高40 mm的岩心试样，便于放入变水头渗透容器中。岩心试样按照深度分组，注浆前岩心对照组共15组，注浆后岩心试验组共15组。每组试样3个，单组结果剔除偏离值取均值。由于声波检测属于无损检测，试样按照先检测声波、后渗透试验的顺序进行。试验开始前对试样进行24 h抽真空水饱和处理，模拟富水环境。试样达到近饱和后，将薄膜贴于其各个面并涂抹偶合剂。将声波激发器与接收器紧靠于薄膜，利用TH208声波检测仪激发声波检测各向岩心波速。将完成检测的试样除去薄膜，放入渗透容器中，再进行变水头渗透试验。试验采用南京土壤仪器厂生产的TST-55型渗透仪，配直径7 mm、长度2.5 m变水头管，管外刻度板的最小分度为1 mm。

4 试验检测结果及分析

4.1 渗透试验结果及分析

1号孔为注浆前成孔，而

2—4号孔为注浆后成孔。通过室内渗透试验和原位压水试验，分别获得了1号、2号孔各深度采取的岩心渗透率(见图2)，以及1—4号孔各岩层段的渗透率(见表1)。其中1号和2号孔相距最近(仅0.35 m)，可近似认为原始地质环境及岩层性质相同。选取二者进行注浆前、后渗透率对照分析，具有较强的对比意义。由图2数据可知，注浆前原始地层透水性强、弱相间，并以14～17 m、22～24 m段为中等透水层，平均渗透率分别为0.29 μm2和0.31 μm2，推测其为富水破碎砂层；注浆后，强弱透水地层透水性均有不同程度改变，中等透水层渗透性大幅降低至弱透水状态。多孔破碎岩层利于浆液注入扩散，止水效果显著。由表1可知，注浆后岩层可注性趋于一致，各深度岩层渗透率接近于1×10-2μm2，均为弱透水层。

表1 压水试验计算结果

图2 室内岩心渗透试验结果

4.2 岩层声波检测结果及分析

通过声波测井试验与室内岩心波速检测，分别得到1—4号孔岩层波速，以及1号、2号孔各深度岩心波速，如图3所示。由图3可知，1号孔14～17 m、22～24 m段平均波速为1 855 m/s，低于整体平均波速2 121 m/s。注浆后2号孔整体岩层平均波速为2 741 m/s，岩层波速明显提高，14～17 m及22～24 m原低波速区段均值波速提升38%，局部波速甚至高于3 000 m/s。3号、4号孔整体波速均值分别为2 720、2 699 m/s，在原低波速区段平均波速高于1号孔42%、39%。判断该区段岩层为强风化压碎砂岩，岩体变形性强，裂隙和孔隙大且连通性好，浆液对孔隙有效填充，从而波速大幅度提高。该规律与Kohkichi等[6]的结论相近。注浆后各深度岩心的波速与渗透性的变化方向相反，变化幅度一致，表明波速可有效预测注浆岩层渗透性变化。

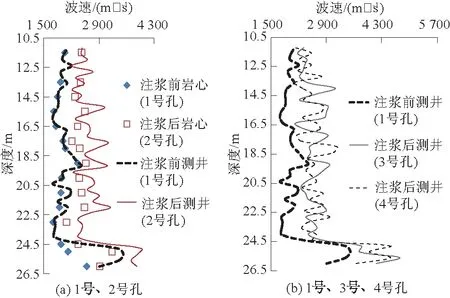
图3 声波波速检测结果

4.3 富水砂岩波速-渗透率模型分析

模型中假定流体波速Vf与骨架波速Vm不变，依照Kamel等[13]岩体试验结果取值Vf=1 648 m/s，Vm=5 492 m/s。将以上1号、2号孔室内岩心波速与渗透率试验数据代入式(8)进行回归分析。拟合曲线如图4所示，拟合参数如表2所示。

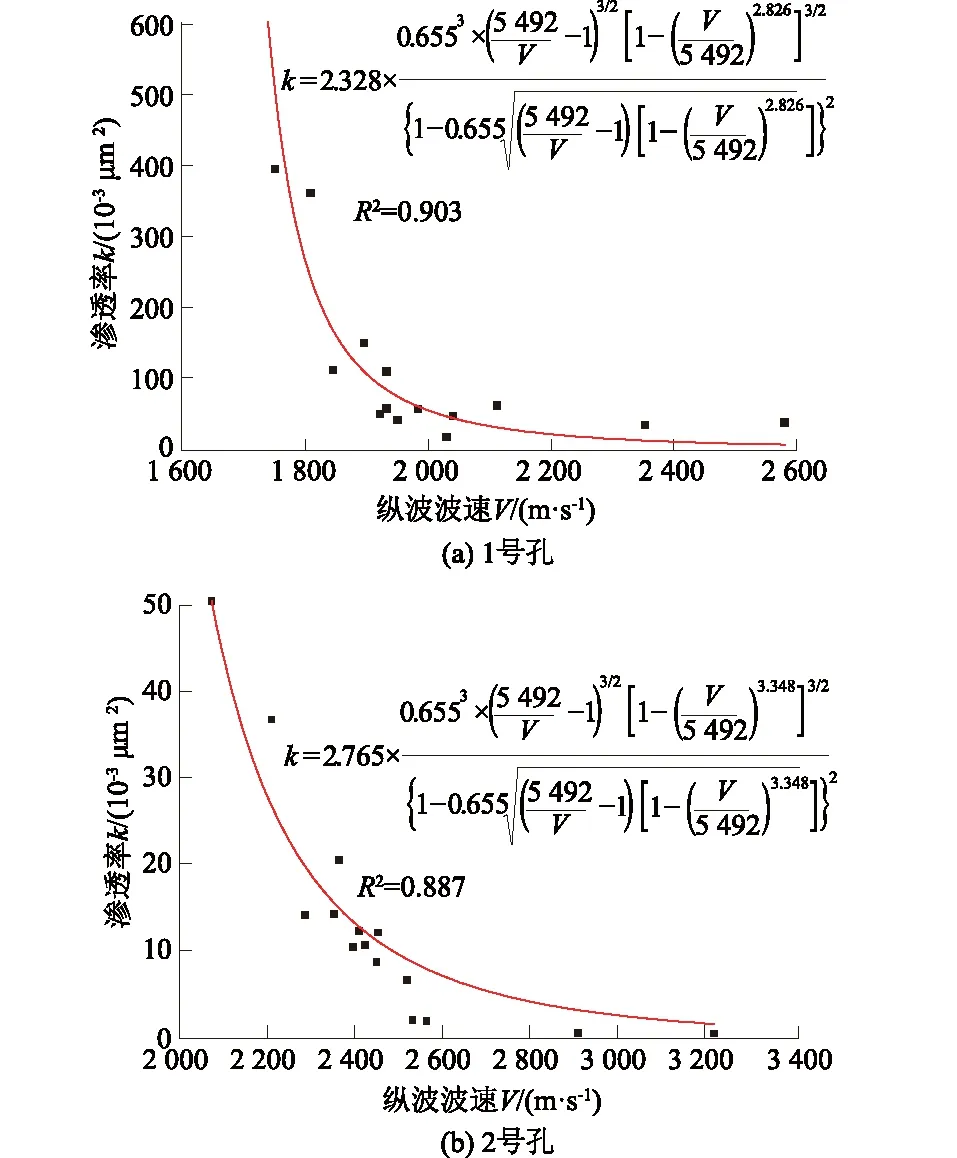
图4 1号孔和2号孔岩心波速-渗透率拟合曲线(Vm=5 492 m/s)

表2 波速-渗透率模型拟合参数

两组拟合所得的决定性系数R2分别为0.903和0.887，试验数值与模型拟合度较高，证明该公式中波速可以较好地反演砂岩渗透率，2号孔拟合度相对1号孔偏低。

由图4可知，砂岩渗透率随波速增大而降低，呈非线性关系，且渗透率的变化率随波速的增大而减小，并存在变化分界点，即:波速低于分界点时，渗透率随波速变化的幅度大；当波速高于分界点时，渗透率随波速变化的敏感度降低。式(8)中波速反映了渗流空间占比与渗透率的关系。当波速接近纯水中的波速1 640 m/s时，岩体内固相几乎不存在，渗流不受阻碍；当波速接近砂岩骨架波速5 492 m/s时，将不存在渗流通道，渗透率将降为0，即β′为0。

图5 注浆砂岩岩心及浆脉

4.4 注浆对波速-渗透率模型的影响及修正

式(8)中岩性指数x是表征岩土颗粒性质及空间结构的重要参数。注浆通过渗透、挤密、劈裂等作用使浆脉与原岩骨架形成新的复合岩土结构，改变了地层性质，如图5所示。这导致图4(a)曲线中岩性指数x与图4(b)不同。浆脉主要成分为硅酸盐水泥，其骨架波速为3 000 m/s[18]，低于砂岩骨架波速，因此新的岩土结构骨架波速应介于二者之间。对2号孔数值拟合时，采用原砂岩骨架波速，导致拟合度相对偏低，需修正骨架波速，对数据重新拟合。

根据Kamel等[13]的试验研究可知，岩体骨架声波时差Δtm与岩性指数x存在以下关系,即

x=55 196Δtm-0.884 3。

(9)

由于Δtm=1/Vm，注浆前、后x比值存在以下关系,即

(10)

式中:x1、x2分别为注浆前、后岩性指数；V1、V2分别为注浆前、后波速;55 196和0.884 3为经验系数。

将表2中的参数注浆前骨架波速V1=5 492 m/s，岩性指数1/x1=2.826及未修正注浆后拟合所得的岩性指数1/x2=3.348代入式(10)，计算得到注浆后岩体骨架波速修正值V2为4 534 m/s。将修正波速V2代入式(8)的Vm，重新进行回归分析，得到图6。由图6和表2分析，拟合曲线决定系数R2达到0.908，与修正前相比拟合度明显提高。这证明了注浆影响了模型参数，但未改变波速与渗透率间的函数关系。

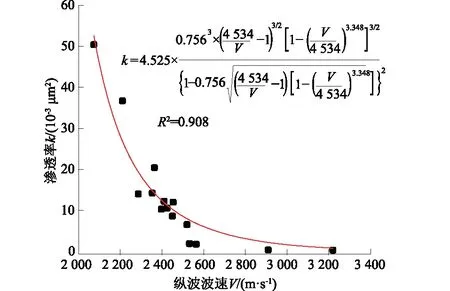
图6 2号孔岩心波速-渗透率拟合曲线(Vm=4 534 m/s)

4.5 模型工程检验

以上回归分析针对的是室内岩心试验结果，分析对象仅1号孔与2号孔岩心，尚无法排除试验偶然性。利用原位声波测井数据计算理论渗透率，与压水试验测得的试验值对比，对模型进行再次验证。

为验证模型在工程中的可靠性，将1—4号孔的测井波速代入含表2修正参数的式(8)中，计算得到各深度逐点岩层渗透率。通过式(11)进行深度加权平均计算，将测点渗透率计算为测段平均渗透率。

(11)

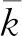
表3 1号与2号孔岩层试验渗透率与计算渗透率对比

表4 3号与4号孔岩层试验渗透率与计算渗透率对比

分析表3可知，注浆前砂岩渗透率计算结果误差介于7.2%～12.2%，注浆后砂岩渗透率计算结果误差介于14.2%～21.4%，对注浆后模型参数修正后，计算误差减小至11.2%～12.3%。由于浆脉影响，式(8)中的骨架波速将比实际值偏大，未修正前计算结果高于修正计算值，相对差值随深度而增大。由表4可知，采用修正模型计算获得的3号、4号孔渗透率误差介于8.4%～12.4%。

因此，本文所提出的注浆富水砂岩波速-渗透率修正模型能够根据岩层纵波波速较好地反演注浆后岩层渗透性的变化。

5 注浆效果评价应用

对富水破碎砂岩注浆效果进行定量评价，一般可以通过岩心试验获得数据。但由图3可知，原位试验波速高于室内岩心波速。根据李晓昭等[19]的研究，产生该偏差的主要原因是岩心由地层取至地表，应力状态改变，内部裂隙受弹性作用而扩张，导致波速降低。富水破碎岩体受该扰动更为明显，裂隙扩张甚至影响岩心渗透率，而利用测井波速反演岩层渗透率，可避免岩心试验存在的偏差。

对于富水破碎岩层，止水效果是注浆效果评价体系中的一个重要方向。渗透率降低幅度η可作为注浆对岩层抗渗性改善的量化值，反映岩体渗透性变化，作为岩体抗渗性提升评价指标。其表达式为

(12)

式中:k1为注浆前岩层渗透率;k2为注浆后岩层渗透率。但由于存在原渗透率较低而注浆后渗透率变化较小的岩层情况，单从渗透率的变化幅度不足以体现注浆后岩层的透水性。

根据规范[20]可知渗透系数<10-4cm/s，渗透率<0.1 μm2时，岩体为弱透水性，将岩层现状渗透率k作为透水性指标，并以0.1 μm2为弱透水判定值判断岩层透水性。k、k1、k2值可通过压水试验获得，但压水试验结果仅代表整体测段平均渗透性。为提高检测精度，通过声波测井获得各深度岩层纵波波速V，将V代入式(8)获得注浆前、后岩层计算渗透率，以计算渗透率表示指标中k、k1、k2值，突破了压水试验试段检测的局限，实现了渗透率的逐点检测和对细部岩体的注浆止水效果评价。

根据以上评价方法，分析本文案例中的地基注浆效果。将图3中的测井波速代入式(8)中，以图4(a)参数计算注浆前岩层渗透率，以图6参数计算注浆后岩层渗透率，并通过计算渗透率获得岩层透水性指标与抗渗性提升指标，如图7、图8所示。

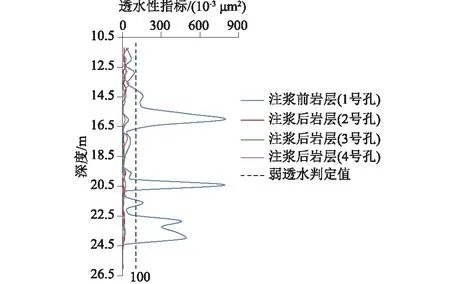
图7 岩层透水性指标

图8 岩层抗渗性提升指标

由图7可知，注浆前34%测点岩层渗透率高于0.1 μm2，为中等透水岩层，主要分布于深度14～17 m及22～24 m，与室内试验判一致，并发现20.5 m深度细部岩层透水性较大。注浆后所有测点岩层渗透率均低于0.1 μm2，透水性降低至弱透水，符合施工要求。根据图8数据显示，2—4号孔平均抗渗性提升率分别达到0.86、0.78、0.77，超过40%测点岩层抗渗滤提升指标在0.9以上，注浆止水效果显著。数据表明该地基注浆后整体及局部岩层抗渗性得到改善，注浆效果达到预期标准。该评价方法适用于注浆富水砂岩渗透性检测，通过声波测井获取各深度岩层渗透性，判断注浆止水效果。