基于BIM的精细化土石方量计算方法

(中铁第四勘察设计院集团有限公司 城市轨道与地下工程设计研究院，武汉 430063)

1 研究背景

在水利水电、公路铁路、城市轨道交通等各种土木工程中，土石方工程量往往都是影响工程进度和技术经济指标的重要参数，因此，在工程的各个设计阶段中，都需要快速、准确地计算土石方量。土石方量的大小主要由地形曲面和开挖面形状决定。传统的土石方量计算方法有断面法、方格网法、TIN(Triangulated Irregular Network)法、体积法等[1-2]，计算过程都比较繁琐，而且计算效率和精度也比较低，尤其是对于地形复杂或者开挖范围较大的工程。

近几年来，BIM(Building Information Model)技术在土木工程领域迅速发展，基于BIM技术进行工程的全过程正向设计，也已经成为行业发展的大趋势[3-4]。由于BIM在设计成果可视化、信息化、智能化等方面都具有巨大的优势，因此，如何利用BIM 技术，精确计算大型复杂工程的土石方量，成为工程设计和研究人员共同关心的问题之一。

目前，工程设计中广泛应用的BIM设计软件都是通用软件，必须结合土木工程行业的特点和需求进行二次开发[5-9]，才能真正发挥其优势。Civil 3D软件是Autodesk公司开发的面向基础设施行业的BIM设计与开发软件，曲面模拟功能比较强大，可以处理多种类型的原始地形资料，因此，在土石方工程量计算中得到广泛应用。江宝刚[10]利用Civil 3D软件实现了开挖工程量计算，张仁杰等[11]、余剑[12]、樊旭宏[13]、覃锋[14]、张生喜[15]也先后利用Civil 3D软件实现了土石方量计算，解决了传统土石方量计算精度低、耗时长的问题。

但是，由于复杂地形曲面模拟无法得到精确解，在利用Civil 3D软件进行土石方工程量计算时，也就无法保证计算结果满足精度控制要求。此外，虽然Civil 3D软件具备开挖面与地形曲面相交计算(工程上常称为放坡计算)的处理功能，但是在地形面和开挖面较为复杂时，操作过程非常复杂，无法实现自动处理。

为此，本文针对大型土木工程的土石方量计算特点和需求，对复杂地形曲面模拟和开挖面自动放坡计算方法进行了研究，提出了基于BIM的精细化土石方量计算方法，并通过对Civil 3D软件的二次开发来实现，以提高其计算效率和精度。

2 地形曲面模拟方法

工程常见的原始地形资料类型主要包括点文件、等高线文件、DEM(Digital Elevation Model)文件等。由于地形曲面是不规则曲面，在进行计算或者显示时，通常只能采用三角形网格来离散模拟。如果原始地形资料是点文件或者等高线文件，可以直接将不规则分布的地形数据点作为三角形网格的节点，生成不规则的三角形网格。如果原始地形资料是DEM文件，因为已知数据点呈规则分布，所以可以直接生成规则的三角形网格。

在利用Civil 3D软件模拟地形曲面时，需要针对不同类型的数据源采取不同的操作方法，有时还需要进行反复检查和修正，才能得到比较符合实际的原始地形曲面[16]。此外，三角形网格尺度的选择也高度依赖软件使用者的工程经验，而且计算结果的精度也无法量化。为此，本文结合大型土木工程的特点，提出采用分片薄板样条插值函数和三角形网格自动加密技术相结合的方法，来实现大范围复杂地形曲面的精细化模拟。

2.1 分片薄板样条插值

对于大型土木工程，地形图范围和数据量较大，精细化建模涉及的数据存储和计量计算庞大。为了提高计算效率、降低对计算机硬件配置的要求，本文采用分片模拟的解决思路和方法。

将Civil 3D导入的各类型原始地形资料统一处理为高程点数据，并将计算范围分成若干个长方形的子域。对于高程点数据特别稀疏的区域，可适当增加子域大小;对于高程点数据特别密集的区域，则可适当减小子域大小。然后，在每个子域上采用薄板样条插值函数来模拟地形曲面。

薄板样条插值法是一种典型的精确插值方法，经常用于高程插值[17]。薄板样条插值函数能精确拟合已知数据点，并将地形面模拟成一个曲面，因此，其模拟精度要高于常用的线性插值方法。

任意点的高程表示为

(2)

对于任意子域，提取域内地形面上的坐标点，作为已知信息输入方程组(式(2))，求解后即可得到该子域的薄板样条插值函数(式(1))。对于子域内任意点，将其水平坐标代入薄板样条插值函数(式(1))，即可求得其高程。

2.2 三角形网格自动加密

三角形网格分为规则和不规则2种。规则三角形网格的拓扑结构和生成方法简单，且只需要存储高程坐标，数据存储量约为相同节点数的不规则三角形网格的1/3。不规则三角形网格的拓扑结构相对复杂，需要通过复杂的算法来实现网格生成，但是其网格大小可以与地形面曲率相关，因此，其模拟精度要高于相同单元数的规则三角形网格。

在Civil 3D软件中，无论是采用规则三角形网格，还是采用不规则三角形网格来模拟地形曲面，都存在一个共同问题：网格尺度应该如何选择，才能保证计算结果满足精度控制要求？换句话说，当软件使用者根据工程经验选择了地形面模拟的三角形网格尺度后，如何知道其计算结果的误差？由于地形曲面模拟无法得到精确解，只能通过加密三角形网格来得到相对更准确的模拟结果，因此，本文采用加密前后计算结果的相对误差来控制计算精度。

三角形网格的加密方法主要有2种：网格重生成和网格细分。网格重生成方法是采用相对更小的网格尺度，通过网格生成算法来重新生成新的三角形网格，主要适用于不规则三角形网格。网格细分则是连接三角形的各边中点，将其直接细分成4个小三角形，或者连接三角形的形心及各边三分点，将其直接细分成9个小三角形。显然，网格细分方法的数据量相对较大，但是其计算过程简单，计量计算相对较小，尤其是对于规则三角形网格。

综上，本文采用规则三角形网格来模拟地形面，并采用网格细分方法进行加密。具体步骤如下：

(1)首先将子域离散成10 m×10 m的正方形，再进一步将每个正方形分为2个直角三角形，得到地形面的一级三角形网格。

(2)按照第3节介绍的开挖面放坡计算方法，生成三维开挖实体，得到各开挖高程的土石方工程量。

(3)连接三角形的各边中点，将其直接细分成4个小三角形，得到加密后的地形面三角形网格。

(4)重新进行开挖面放坡计算，生成加密后的三维开挖实体，得到加密后的各开挖高程的土石方工程量。

(5)利用加密前后的土石方工程量，计算得到相对误差，若不满足计算精度控制要求，重复第(3)和第(4)步。

3 开挖面自动放坡计算方法

开挖布置图通常按照建筑物布置要求和边坡安全要求来确定，包括控制点坐标、平台高程、开挖坡度及边界位置等信息。在建立BIM时，需要按照开挖布置图的信息，从控制点坐标开始，逐步生成各开挖平台面和开挖坡面，并最终与地形曲面相交，得到边界曲线。整个计算过程称为放坡，其中，主要难点在于计算开挖边界曲线。

Civil 3D软件具备放坡计算功能，但是在地形面和开挖面较为复杂时，操作过程非常复杂，无法实现自动处理。为此，本文提出一种开挖面自动放坡计算方法，通过开挖面与地形面三角面片的拓扑及几何计算，得到准确的开挖边界曲线。为便于描述，作如下定义(如图1所示)。

图1 开挖面示意图

(1)内部开挖面：开挖面中与开挖边界无关的多边形平面，所有顶点均不在开挖边界上(如图1所示的S1面)。

(2)边界开挖面：开挖面中与开挖边界有关的多边形平面，至少有一个顶点在开挖边界上(如图1所示的S2、S3、S4面)。

(3)内部控制点：开挖面中与开挖边界无关的顶点(如图1所示的P1点)。

(4)边界控制点：开挖边界曲线上同时与2个边界开挖面有关的顶点(如图1所示的P2、P3点)。

(5)开口线：开挖边界曲线上2个边界控制点之间的多段线(如图1所示的L2线)。

实际上，一个复杂的三维开挖面往往由多个内部开挖面和边界开挖面组成。内部开挖面的计算相对比较简单，其顶点或是已知的控制点，或是按照3个平面求交点即可得到。边界开挖面的计算涉及地形面，相对复杂一些，但是归纳起来可以分为2类问题：由内部控制点推求边界控制点、由边界控制点推求开口线。

3.1 由内部控制点推求边界控制点

以图1所示开挖面为例，已知内部控制点P1、沿边界开挖面S2和S3的交线L1，推求边界控制点P2，属于由内部控制点推求边界控制点问题。图2是局部开挖面和地形面的俯视图，地形面采用规则三角形网格模拟(图2只画出了局部的三角形网格)。待推求的边界控制点P2实际上是开挖面与三角形网格的交点。

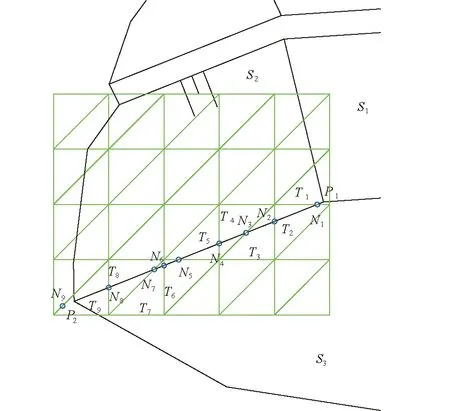
图2 由内部控制点推求边界控制点示意图

计算方法如下：

(1)通过内部控制点P1的平面坐标，判断其垂直投影到地形面上后所在的三角形T1。

(2)计算直线P1P2与三角形Ti在水平投影面上的交点Ni。

(3)分别计算交点Ni在直线P1P2上和三角形Ti上的高程坐标Z1、Z2。

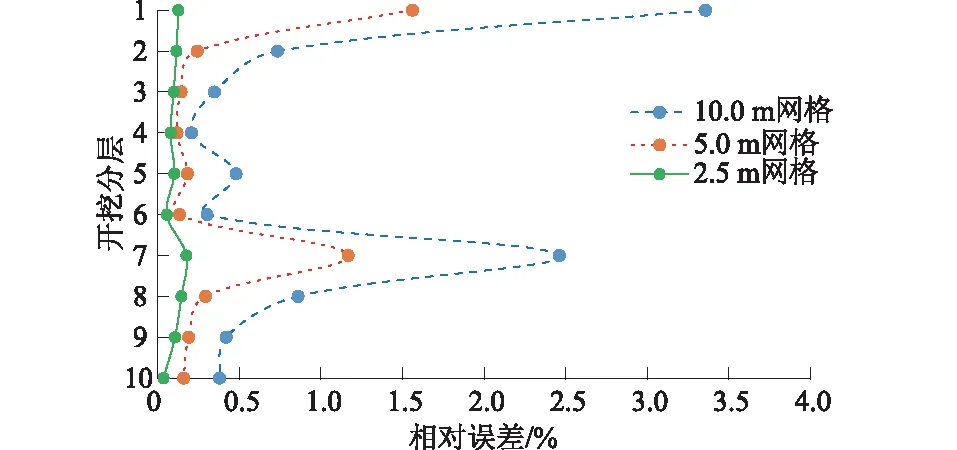
(4)如果Z1

(5)如果Z1>Z2，表明线段上的点已在地形面上方(图2中所示的N9)，则计算直线P1P2点与三角形Ti+1(图2中所示的T9)的交点坐标，即可得到边界控制点P2，计算结束。

3.2 由边界控制点推求开口线

仍然以图1所示开挖面为例，已知边界控制点P2、沿边界开挖面S2，推求开口线L2，属于由边界控制点推求开口线问题。图3是局部开挖面和地形面的俯视图，地形面采用规则三角形网格模拟(图3只画出了局部的三角形网格)。待推求的开口线L2实际上是开挖面与三角形网格相交的多段线。

图3 由边界控制点推求开口线示意图

计算方法如下：

(1)通过边界控制点P2的平面坐标，判断其垂直投影到地形面上后所在的三角形T1。

(2)计算平面S2与S4的交线L3方程。

(3)计算平面S2与三角形Ti的交点Ni。

(4)判断交点Ni与边界控制点P2是否在交线L3同侧。

(5)如果在同侧，表明该交点尚在边界开挖面S2内，则针对相邻三角形Ti+1，重复第(3)和第(4)步。

(6)如果不在同侧，表明该交点已在边界开挖面S2外(图3中所示的N8)，则计算交线L3与三角形Ti+1(图3中所示的T8)的交点坐标，即可得到边界控制点P3及开口线P2P3，计算结束。

采用上述方法计算出开挖面的所有控制点和开口线后，即可利用Civil 3D软件的已有功能，直接在BIM上生成完整的开挖面，并通过其与三维地形实体进行布尔操作，得到开挖实体。实际工程中，通常需要分高程计算开挖量，直接用各高程平面切割BIM即可。在开挖实体生成后，可以直接通过查询各分层开挖实体的属性得到土石方工程量。

4 算例分析

为了验证本文方法的有效性，选取某大型土木工程的部分开挖面为例，进行计算分析。该算例原始地形资料为等高线文件，计算范围为500 m×300 m，将其分为100 m×100 m的子域进行地形模拟(如图4所示)。

按文中所述方法进行计算，初始三角形网格尺度取为10 m，以各层开挖的土石方量相对误差≤0.2%作为精度控制标准。经过3次网格细分后，当三角形网格尺度为1.25 m时得到满足精度要求的计算结果。图5是生成的分层开挖实体。

表1是不同网格尺度下的各层开挖土石方工程量，其中，各网格尺度下的计算结果相对误差均以将其加密一次后的计算结果为参照。图6是不同网格尺度时的各层土石方量相对误差曲线。

注:图中方框中的数字表示高程(m)。图4 算例子域划分Fig.4 Subdomain division of numerical example图5 算例分层开挖实体Fig.5 Layered excavation entities ofnumerical example

表1 土石方量计算结果

图6 不同网格尺度时的各层土石方量相对误差

从图1、表6中各土石方量计算结果可以发现：

(1)随着地形面三角形网格尺度逐渐减小，无论是总的开挖土石方量，还是各分层的土石方量，计算结果都更加精确。

(2)对于开口线附近的开挖层，比如第1和第7层开挖，由于开挖深度相对较浅，计算的土石方量相对误差受地形面模拟精度的影响更大。

(3)对于土石方量较大的开挖层，比如第10层开挖，由于开挖深度较深，计算的土石方量相对误差受地形面模拟精度的影响较小；但是由于其涉及的地表范围大，计算的土石方量绝对误差较大。

5 结 语

针对大型土木工程的地形面范围大、开挖面复杂、土石方工程量计算繁琐的特点，本文研究并提出了基于BIM的精细化土石方量计算方法。主要取得了以下研究成果：

(1)提出了模拟大范围地形面的分片薄板样条插值函数方法，采用规则直角三角形网格来离散地形面，并通过网格自动加密来提高和控制地形面模拟精度。

(2)提出了开挖面的自动放坡计算方法，通过开挖面与地形面三角面片的拓扑及几何计算，由内部控制点推求边界控制点再推求开口线。

(3)在Civil 3D软件的基础上，通过二次开发，实现了大型土木工程的精细化土石方量计算。

地形曲面的精细化模拟除了可以提高土石方量计算的精度，还可以提高BIM的可视化效果。当然，三角形网格的自动加密也必然带来数据量的增加。对于实际应用的很多场景，比如工程全景或者BIM与GIS融合时，为了提高图形显示的速度，又需要对BIM进行轻量化处理。自动加密的规则三角形网格中正好包含了多套不同尺度的网格，可以适应不同精度的地形曲面模拟需求，因此有望在BIM的轻量化中得到应用，这也是下一步需要研究的课题。