基于贝叶斯优化LightGBM的大坝变形预测模型
2021-07-1223
23
(1.河海大学 水利水电学院,南京 210098; 2.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098; 3.三峡大学 水利与环境学院,湖北 宜昌 443002)
1 研究背景
大坝变形是一种直观可靠的监测指标,可反映各种荷载作用下的大坝工作性态变化[1]。建立精准的大坝变形预测模型,对掌握大坝运行状况,及时进行安全示警具有重要意义。然而大坝在服役期内工作条件复杂,变形具有不确定性、多变等特点[2],传统模型如多元回归、逐步回归等很难准确预测它。此外随着监测技术的发展,采样频率直线上升,大量数据亟待处理,这对预测模型的数据处理能力提出了更高的要求[3]。
近些年来,机器学习领域众多方法,如人工神经网络、支持向量机等被应用于大坝变形预测中,并取得良好表现[4-5]。吉培荣等[6]证实GM(1,1)模型要求原始数据平稳且满足指数分布规律,预测精度受随机扰动影响大。朱军桃等[7]提出了改进支持向量机算法,但其回归性能仍受内部参数很大影响。杨贝贝[8]将小波核函数与支持向量机结合,提出一种新的大坝变形预测方法。卢献健等[9]提出一种结合遗传算法和粒子群优化算法(PSO)优化的BP神经网络大坝变形预测模型。然而这些方法也存在一些弊端,限制了其在工程中的大规模应用,如支持向量机的回归性能受内部参数影响大,人工神经网络易陷入局部最优解,大规模训练样本时计算速度慢,不适用于大规模监测数据处理[10]。
基于此,本文采用一种快速、高效、分布式的基于决策树算法的梯度提升框架LightGBM(Light Gradient Boosting Machine)[11],并应用一种概率寻优方法贝叶斯优化确定模型中存在的超参数[12],以两座运行多年的混凝土坝为例,将所提基于贝叶斯优化的LightGBM模型应用于大坝变形预测中,并与其他方法进行对比,验证模型的合理性和有效性。
2 贝叶斯优化LightGBM框架预测原理
2.1 LightGBM算法原理
大坝变形预测通常需要面临大规模的数据处理,决策树可解释性强且预测速度快,因此基于决策树的算法适用于建立预测模型,通过限制梯度提升框架LightGBM的参数可有效避免决策树易过拟合的问题。
梯度提升(Gradient Boosting)指利用损失函数的负梯度作为回归问题提升树残差的近似值。提升树(Boosting Tree)是以二叉树为基本学习器的一种提升方法,采用加法模型与向前分布算法。模型为
(1)
式中:T(x;Θm)为决策树;Θm为决策树的参数;M为树的个数;fM(x)为提升树。
通过最小化损失函数Loss(y,fm(x))来确定决策树T(x;Θm)的参数:
argminΘmLoss(y,fm-1(x)+T(x;Θm)) 。
(2)
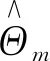
梯度提升决策树(Gradient Boosting Decision Tree,GBDT)结合梯度提升和决策树的特性,效果好且不易出现过拟合。假设一段大坝数据集,即
D={(xi,yi),i=1,2,…,N,xi∈Rs,yi∈R}。
式中:N为序列长度;yi为大坝位移;xi为影响大坝位移因素;s为每个样本特征个数;R为实数集。
计算步骤大体上分为2步,即初始化和得到最终模型。
初始化可得f0(x),即
(3)
式中c为使损失函数极小化的常数值。
(1)进行迭代,迭代次数m可取1,2,…,M。
(2)计算残差rm,i,即
(4)
(3)对(xi,rm,i)拟合一个回归树,得到第m棵树的叶节点区域Rm,j,j=1,2,…,J,J为节点区域个数,计算参数cm,j,即
(5)
(4)更新回归树,即
(6)
式中I为回归树更新时参与迭代的参数。
得到最终模型,即
(7)

GBDT算法处理数据时需要储存特征值及排序结果等,时间和空间消耗大,应用于大坝变形预测研究受到很大限制。LightGBM是对GBDT的一种改进,具体如下:采用histogram算法减少内存消耗,降低计算代价;带深度限制的Leaf-wise的叶子生长策略替代传统的level-wise策略,每次寻找分裂增益最大的叶子分裂,可降低误差,提高大坝预测精度。此外,LightGBM的两个核心技术很大程度上提高了运算速度,满足大坝监测数据处理要求。具体为:基于梯度单边采样技术(Gradient-based One-Side Sample, GOSS),保留大梯度数据,对小梯度数据随机抽样,保持信息增益的同时提高泛化能力;采用特征捆绑(Exclusive Feature Bundling, EFB)技术实现互斥特征的捆绑,降低数据特征规模[13]。
2.2 贝叶斯优化算法框架
应用LightGBM模型进行大坝变形预测时,需要确定最优超参数组合。考虑到机器学习易陷入局部最优解问题,本文引入一种全局优化算法——贝叶斯优化算法(Bayesian Optimization Algorithm,BOA)进行模型参数寻优。贝叶斯优化算法以贝叶斯定理为基础,通过最大化采集函数得到下一个最有潜力的评估点xt,进而评估目标函数值yt,将新得到的(xt,yt)添加到已知评估点集合中,更新概率代理模型依次循环从而得到最优解[14-15]。由于贝叶斯优化算法可以充分利用历史信息,其效率明显高于其他寻优方法。
概率代理模型和采集函数是贝叶斯优化的两个核心部分。概率代理模型分为参数模型及非参数模型两大类,非参数模型具有更高的扩展性,通常能取得满意的预测结果,其中以高斯过程(Gaussian Process, GP)应用最为广泛。采集函数指从输入、观测、超参数空间映射到实数空间的函数,需要平衡利用与探索之间的关系,权衡评估点的分布。
2.2.1 概率代理模型
高斯过程是一个随机变量的集合,一个高斯过程构成为
f(x)~GP(m(x),k(x,x′)) 。
(8)
式中:m(x)为均值函数,m(x)=E[f(x)],通常设置为0;k(x,x′)为协方差函数,k(x,x′)=E[(f(x)-m(x))(f(x′)-m(x′))];f(x)为一个连续函数;x′为随机变量。
考虑0均值的先验分布p(f|X,θ)为
p(f|X,θ)=N(0,∑) 。
(9)
式中:X为训练集;f为未知函数的函数值集合;∑为k(x,x′)构成的矩阵。
存在观测噪声ε时,p(ε)=N(0,σ2),σ2为方差,得到似然分布为
p(y|f)=N(f,σ2I) 。
(10)
式中:y为观测值集合;I为单位矩阵。
进而得到边界似然分布为
p(y|X,θ)=N(0,∑+σ2I) 。
(11)
根据高斯过程性质,可得到
(12)

p(f*|X,y,X*)=N(〈f*〉,cov(f*)) ; (13)
(14)
式中:〈f*〉为预测均值;cov(f*)表示预测协方差。
2.2.2 采集函数
采集函数是确定下一评估点的重要依据,选用基于置信区间策略(GP-UCB)时下一个评估点为
(16)
式中:参数βt为平衡探索和开发的常数;μt(x)为均值;σt(x)为标准差。
2.3 基于贝叶斯优化LightGBM 的预测模型
2.3.1 模型执行步骤
利用贝叶斯优化对LightGBM进行参数寻优时,以LightGBM的不同超参数组合作为自变量x,以五折交叉验证评估得到的均方误差(MSE)作为贝叶斯框架的输出f。贝叶斯优化LightGBM的大坝变形预测模型具体步骤如图1所示。

图1 LightGBM大坝变形预测流程
2.3.2 评估指标
为衡量大坝变形预测模型的精度优劣,选取决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)3个指标进行评价,其计算公式分别为:
(17)
(18)
(19)

3 实例应用
某混凝土重力拱坝最大坝高为76.3 m,坝顶弧长419 m,坝顶宽8 m,最大坝底宽53.5 m。选取PL26-1及PL8-2两垂线测点为例分析,此外为验证所提模型的适用性,对某重力坝亦选取两引张线测点EX5-2、EX6-2。本文运行平台为AMD2600 CPU,32 G内存,编程语言为Python,基于KERAS深度学习框架进行数据处理、参数选择及建立LightGBM模型。采用多元线性回归(Multiple Linear Regression,MLR)、支持向量回归机(Support Vector Regression,SVR)、多层神经网络(Multi-Layer Perceptron,MLP)作为对比方法,验证其优越性。
3.1 数据处理
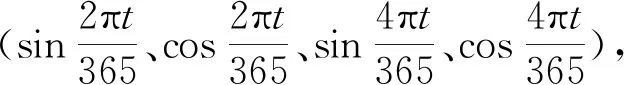
3.2 参数选择
本文中LightGBM算法包括学习率learning_rate、最大深度max_depth、子叶个数num_leaves以及子叶最小数据数min_data_in_leaf共4个参数。给定的参数范围内,分别采用贝叶斯优化和随机搜索优化,以五折交叉验证的均方误差(Mean Squared Error,MSE)作为目标函数,控制迭代次数为100次,得到LightGBM 参数及优化值,如表1所示。
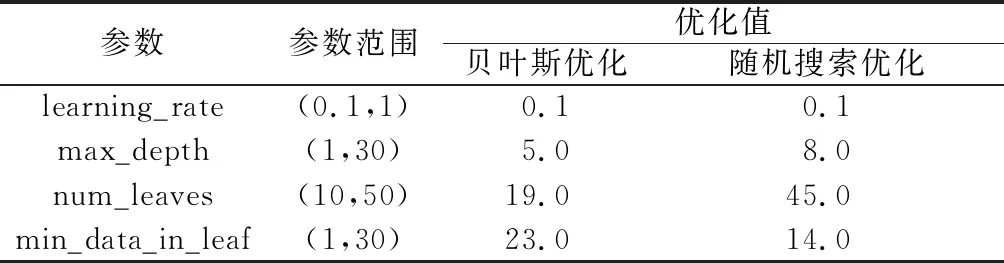
表1 LightGBM 参数及优化值
为便于比较,绘制训练集MSE变化曲线,见图2。迭代100次随机搜索用时110 s,在第55次寻得最优,贝叶斯优化用时65 s,在第35次寻得最优,且随机搜索MSE值0.222 mm2仍大于贝叶斯优化MSE值0.128 mm2。实验结果表明,贝叶斯优化能够根据采样点的结果进行调整主动寻优,在搜索过程中整体稳定,在较少时间内得到最优参数组合,而随机搜索依赖于迭代次数;最优参数组合的出现具有随机性、效率低等特点;本次实验中贝叶斯优化表现优于随机搜索(图3),在LightGBM的参数寻优中更具优势。
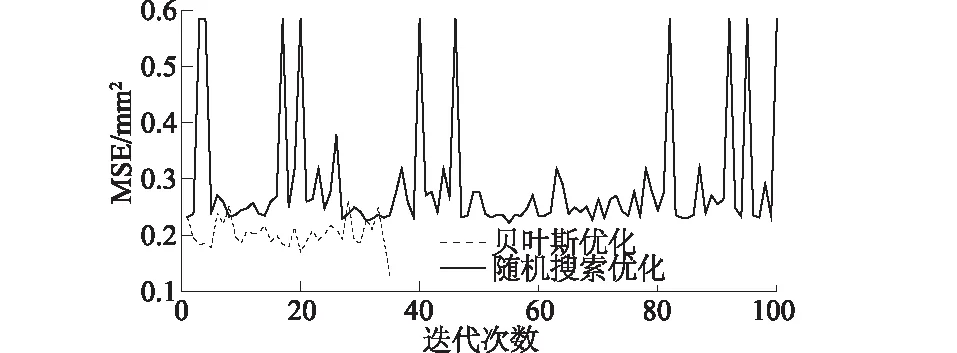
图2 训练集MSE变化曲线
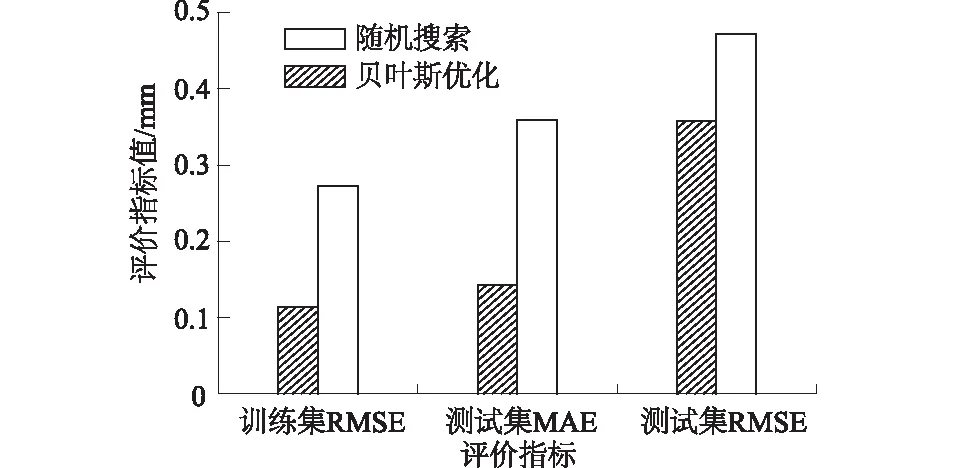
图3 不同优化方法模型评价指标对比
3.3 预测结果分析
采用上述建立的BOA-LightGBM模型对大坝位移进行预测,将预测值与多元线性回归(MLR)、支持向量回归机(SVR)以及多层神经网络(MLP)进行对比,各模型参数及预测结果如表2所示。表2中c′为支持向量回归机SVR的惩罚系数,gamma是SVR中反映数据映射到新的特征空间后的分布的参数,Hidden-layer-sizes是MLP的隐藏层神经元数目。

表2 不同模型参数比较
从图4、图5可以看出,BOA-LightGBM模型的预测值与实测值变化趋势整体一致,且在真实值附近上下均匀波动,对比其他模型,虽然预测值趋势一致,但曲线较光滑不能反映真实值的波动情况。分析图5中残差可以看出,相比于其他预测模型,BOA-LightGBM预测残差均值小,且分布集中,说明模型预测结果较好。

图4 不同模型大坝位移预测结果与实测值比较
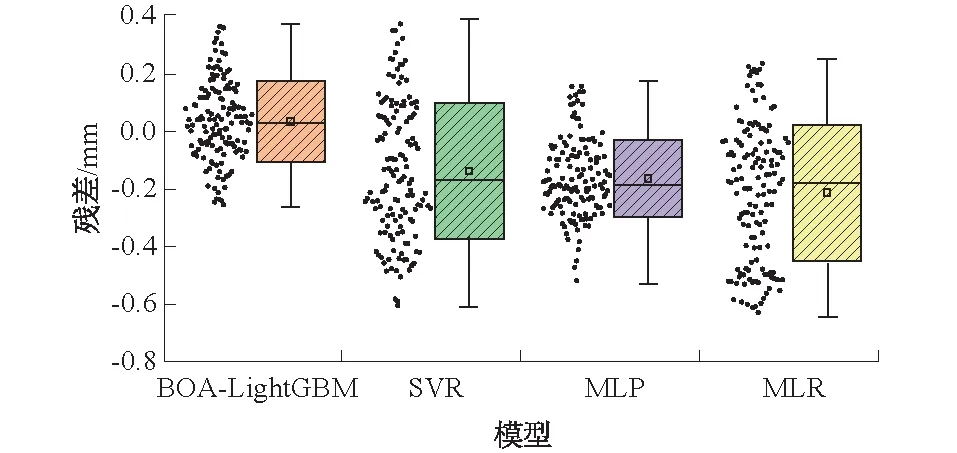
图5 不同模型预测残差
由表3可知,在R2、MAE及RMSE指标中,BOA-LightGBM预测模型均优于SVR、MLP、MLR等模型,即BOA-LightGBM模型精度较高。
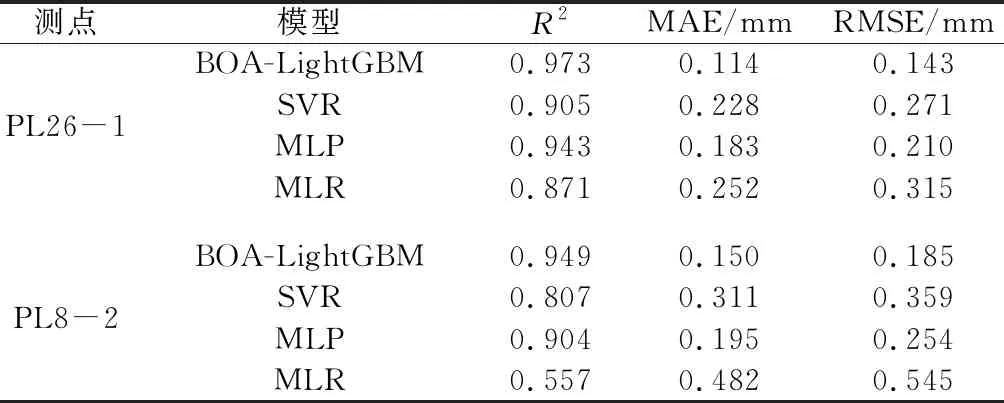
表3 重力拱坝测点不同预测模型结果比较
如表4所示,所提模型在3种评价指标下均具有良好表现,显著优于传统统计模型MLR。综上所述,本文基于BOA-LightGBM的大坝变形预测模型具有较高的精度和很好的泛化能力。
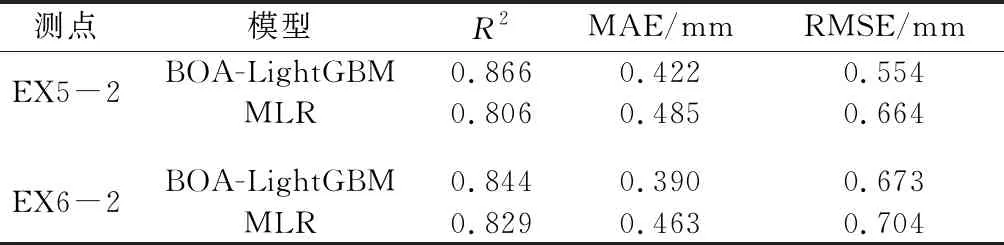
表4 重力坝测点结果比较
此外,LightGBM可以输出各个特征对预测结果的贡献程度,图6为PL26-1测点各影响因素重要性分布,可以看出时效因子θ、水位因子H以及4个温度因子对结果影响显著,这是由于该测点附近存在贯穿裂缝,与该重力拱坝实际状况相符[16]。而PL8-2测点水位因子H贡献度为23.25%,时效因子θ贡献度为14.43%,验证了该模型的可靠性。
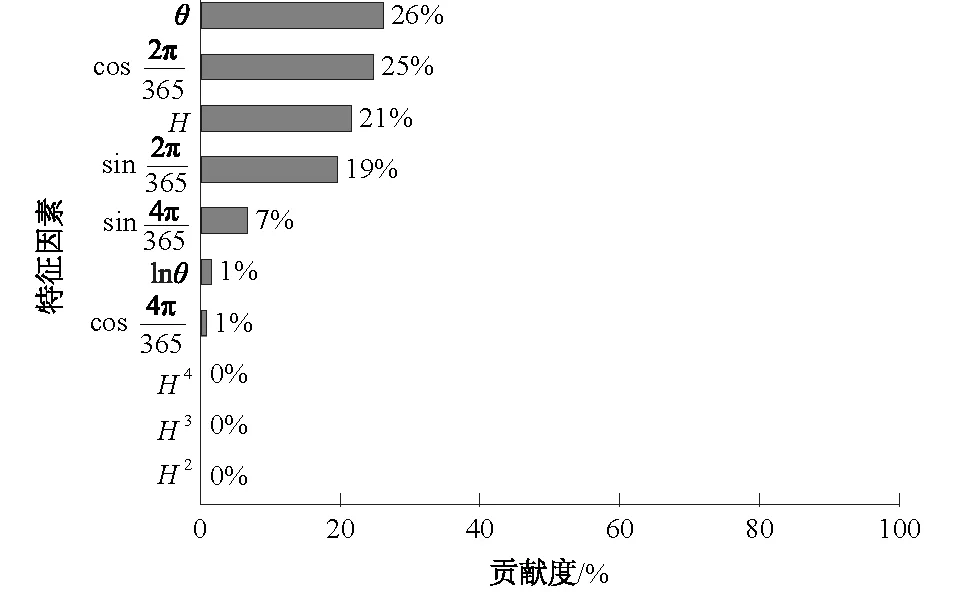
图6 大坝预测模型各特征因素贡献度
4 结 论
本文提出了一种基于LightGBM的大坝变形预测模型,该模型改善了现存模型适用于小样本、易陷入局部最优等问题,得到如下结论:
(1) 与随机搜索相比,贝叶斯优化可充分利用历史信息,减少不必要的目标函数评估,提高参数搜索效率。
(2) 提出一种基于贝叶斯优化与五折交叉验证的模型搜索方案,结合LightGBM模型应用于大坝变形预测中,与其他模型相比,所提模型具有更高的预测精度和泛化能力,在3种定量评估指标中均取得最好表现。
(3) LightGBM可对输入参数的重要性进行评估,对影响大坝变形的特征进行筛选,从而确定对大坝变形影响更显著的因素,为后续的安全评估工作提供参考。
