多样、多元 、多维，实现对数学知识的深度理解

薛利敏

【摘 要】概念是客观事物本质属性的概括，学生理解概念的过程即是对概念所反映的本质属性的把握过程。概念是思维形式之一，也是判断和推理的起点，所以概念教学对培养学生的思维能力起重要作用。为准确把握概念的本质属性，加深学生对概念的理解，笔者从情境探究、交流表述、辩证练习几方面来加深学生对概念的理解。

【关键词】多样情境 多元表征 多维思考

教育心理学告诉我们，学生对于概念的理解既非来自外部的信息，也不是原来的长时记忆，而是思维过程的产物，是对概念的内涵和外延进行详细的“深加工”。教学中，教师可以创设多样的情境，引导学生产生多维的思考，促使学生对概念的细节把握得更准确，对知识的理解更加完善。下面，笔者结合苏教版数学四年级下册“三角形三边的关系”一课的教学谈谈自己的思考。

一、多样情境：在探究中辩证地理解概念

情境一：小组活动，为探究提供支撑（每组准备四根小棒）

出示实验要求：

（1）从四根小棒中任选三根，围一围。

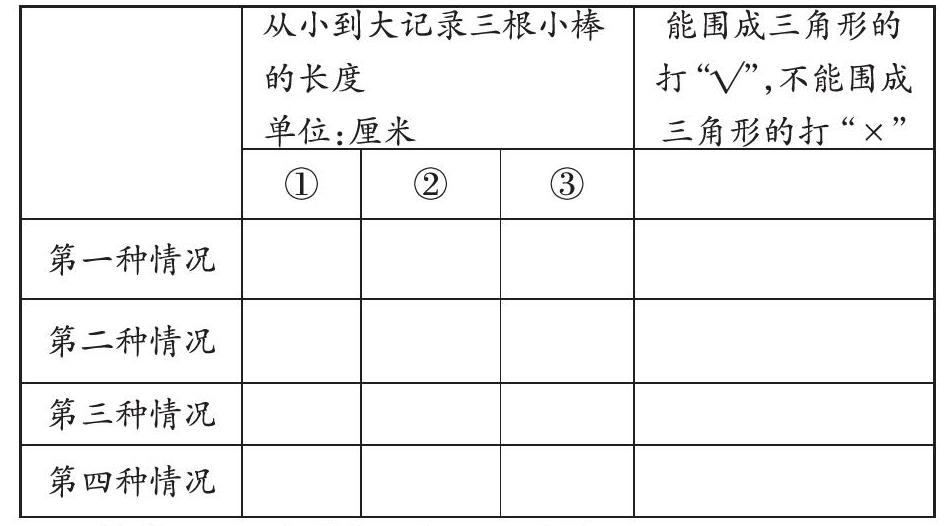
（2）从小到大记录每一根的长度，能围成三角形的打“√”，不能围成三角形的打“×”，

学生在小组内任选三根小棒围一围，将结果记录在下面的表格内。

从小到大记录三根小棒的长度

单位：厘米 能围成三角形的打“√”，不能围成三角形的打“×”

① ② ③

第一种情况

第二种情况

第三种情况

第四种情况

情境二：观察分析，发现三边关系

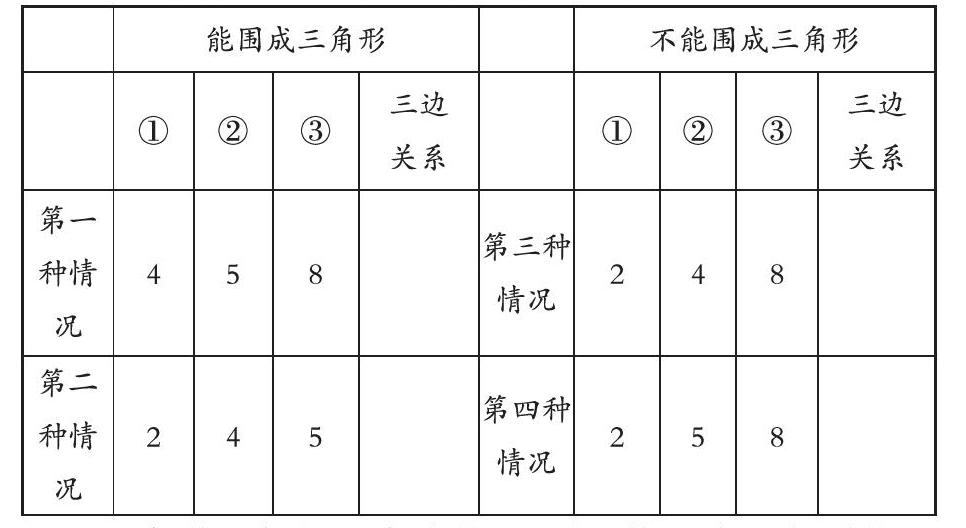
学生分类整理探究的结果，出示表格。

能围成三角形 不能围成三角形

① ② ③ 三边

关系 ① ② ③ 三边

关系

第一种情况 4 5 8 第三种情况 2 4 8

第二种情况 2 4 5 第四种情况 2 5 8

要求学生仔细观察表格，思考：能围成三角形的三边到底有什么奥秘？学生通过举例、计算、比较，发现“三角形两根小棒长度和大于第三根小棒，能围成三角形”。教师质疑：第三、第四种情况中也有两根小棒长度和大于第三根小棒的现象，为什么不能围成三角形？引导学生得出“两根较短小棒的长度和小于第三根小棒，不能围成三角形”的结论。

情境三：动手验证，完善发现

出示活动要求：

①画一画：任意画一个三角形。

②量一量：量出三角形的各边长度。（单位：毫米）

③算一算：算出任意两边之和与第三边长度的关系。

學生完成后，教师展示不同学生的探索结果，并提问：同学们画的三角形虽然各不相同，但它们有什么共同的特点？引导学生发现“三角形任意两边的长度之和大于第三边”。追问学生：画出的三角形中有没有不符合这一性质的？学生换一角度去关注，发现只要是三角形，都符合“三角形任意两边长度之和大于第三边”这一性质。

解读：

在探索三角形三边关系的过程中，学生经历了“小组合作围三角形—观察分析初步感悟三边关系—动手画验证三边关系”这三个学习情境，在第一个情境中学生分组直观操作摆三角形，并记录探究结果，为后面的研究提供了真实的学习资源。第二个情境中学生分类整理摆小棒的结果，观察数据、分析数据、研究关系，通过质疑明白“两根较短小棒的长度之和小于第三根小棒，不能围成三角形”。通过“能与不能”的对比，学生发现：只要其中有一种情况不符合规律，就能判断它是不能围成三角形的。要能围成三角形，必须满足任意两根小棒的长度之和大于第三根小棒。强调了“任意”一词，完善了学生的发现，使其更具严密性。第三个情境中，学生任意画三角形，教师展示学生的作品，通过不完全归纳，发现画的三角形虽然各不相同，但它们拥有共同的特点： “三角形任意两边长度之和大于第三边”，让学生辩证地理解了“三角形任意两边长度之和大于第三边”这一重要性质。

二、多元表征：在交流中凸显对概念的精确理解

语言是思维的工具，数学学习质量的高低往往与数学语言思维建立及使用的熟练水平有密切联系。

1.规范——完整的表述

师：大家整理探索的结果，这是能围成三角形的情况，这是不能围成三角形的情况，仔细观察，你们觉得能围成三角形的三根小棒到底有什么奥秘？和同桌交流你的想法。

生1：两根小棒的长度大于第三根小棒的长度，能围成三角形。

生2：两根小棒加起来的长度和大于第三根小棒的长度，能围成三角形。

师（引导）：你们的发现是否正确呢？请举例说明。

（学生举例说算式，电脑出示：4+5>8，4+8>5，5+8>4）

师：看看第二种情况是否有这样的规律。

（学生自己算一算比一比，指名回答，电脑出示：2+4>5，2+5>4，4+5>2）

师：通过刚才的验证，你们发现能围成三角形的三根小棒的长度有什么关系？

生：三角形两根小棒的长度和大于第三根小棒的长度，能围成三角形。

师（设疑）：那第三种情况（4+8>2，2+8>4）和第四种情况中也满足两根小棒长度之和大于第三边的长度，为什么不能围成三角形呀？

生：因为有两根小棒的长度加起来小于第三根的长度了。

师（点拨）：这两根小棒有什么特点？是呀，在验证时，我们只要发现其中较短的两根小棒长度之和不符合规律，就能判断它是不能围成三角形的。要能围成三角形，必须满足任意两根小棒的长度和大于第三根小棒的长度。（电脑出示：任意）

师（追问）：用你的话说说为什么不能围成三角形。

生：两根较短小棒的长度和小于第三根小棒的长度，不能围成三角形。

2. 简练——精准的表达

数学是具有简洁美的学科，在学生深入理解概念的基础上，也可以进一步缩句。如在用小棒摆三角形抽象为画三角形，再一次验证“三角形两根小棒的长度和大于第三根小棒的长度，能围成三角形”“两根较短小棒的长度和小于第三根小棒的长度，不能围成三角形”后，教师进一步抽象出性质：任意两边之和大于第三边能围成三角形，两边之和小于第三边不能圍成三角形。随后追问：如果两边之和等于第三边能围成三角形吗？通过交流与电脑演示，进一步整合概括：两边之和不大于第三边不能围成三角形。

3.符号化——抽象的表征

最后，教师追问学生：还能用字母来表达刚才的意思吗？学生在学习运算律及长方形面积计算公式、周长公式时已接触过用字母表示数量关系，这时自然想到可以用“a+b>c时， 能围;a+b≤c时，不能围”来表示三角形三边的关系，其中a、b表示任意两边，c表示第三边。这样的表征方式做到了用简洁的符号语言表达丰富的数学规律，有利于发展学生的数学符号意识。

解读：

学生对概念的理解是循序渐进的，刚接触时必须引导学生规范地表述概念，明确每一个要素，理解概念的各个方面，比如“任意”“长度和”等，随着举例的不断丰富与延伸、理解的不断深入，可以将“冗长”的句子浓缩，把握细节即可，如“两边之和”“不大于”等，最后学生对于概念的某些限制条件已充分把握，就可以用符号来表达对概念的精确理解。多元表征让不同思维层次的学生彰显自己对概念的理解，不同层次表征之间的转化，促进了学生对关系、规律的精确理解。

三、多维思考：在辩证练习中提升推理能力

1.由此及彼

完成教材第78页“练一练”第1题。

师（引导）：到现在为止，我们研究的都是三角形两边长度之和与第三边之间的关系，对此，你们有没有其他想法？

生：我想知道三角形任意两边长度的差与三边有什么关系。

师：很好，由长度和联想到长度差，会联想是学习数学的妙招之一。观察第一题中能围成三角形的任意两边长度之差有什么特点。

生：观察发现任意两边长度差小于第三边的长度。

师：算一算刚才画的三角形任意两边长度差，再与第三条边比一比，符合刚才的发现吗？

（生交流）

师：我们又得到了另一个特征，即三角形任意两边长度的差小于第三边的长度。（贴出板书，并用字母表示a-b

2.由顺到逆

师：请大家完整地读一读这两个性质：“三角形任意两边之和大于第三边”   “三角形任意两边长度的差小于第三边”。

（生齐读）

师（启发）：由“三角形任意两边长度的和大于第三边”倒过去想到——？由“三角形任意两边长度的差小于第三边”倒过去想到——？

生1：我想到第三边要小于两边之和，大于两边之差。

生2：我知道第三边在两边之和与两边之差中间。

师：真棒，我们可以确定第三边的取值范围——两边之差<第三边<两边之和，这可以帮助我们解决一些实际问题。

解读：

在学生研究发现三角形任意两边的和与第三边之间的关系后，教师启发学生思考：任意两边的差与三边有什么关系？学生通过观察练习题中能围成三角形的任意两边之差的特点，再算一算自己画的三角形任意两边的差，与第三条边比一比，得出“三角形任意两边长度的差小于第三边”的结论。由两边之和想到两边之差，由此及彼，举一反三，打开了学生的思维视角，使学生的探索有了更深的意义。随后，教师启发学生思考“由‘三角形任意两边长度之和大于第三边倒过去想到——？由‘三角形任意两边长度的差小于第三边倒过去想到——？”得到了第三边与两边之和、两边之差的关系，明确了第三边的取值范围。由顺到逆，学生的思维能力得到了提高，思维更加缜密，对三角形三边关系的认识更加完善、更加丰满，这一发现可以帮助学生很好地解决如下问题：三条线段围成一个三角形，其中两条线段分别长2厘米、7厘米，那么第三条线段最长是（   ）厘米，最短是（    ）厘米。数学课程标准指出：数学知识的教学，要注重知识的“生长点”与“延伸点”，注重知识的结构和体系，引导学生感受数学的整体性，体会对某些数学知识可以从不同的角度加以分析、从不同的层次进行理解。因此在教学中，我们要在学生掌握基础知识、基本技能的情况下，发掘深层次的问题，激发学生多维度思考，关注学生推理能力和创新意识的培养。

多样，是对学习内容的要求;多元，是对学习形式的要求;多维，是对学习方法的要求。

【参考文献】

陈培群.在“多彩”的课堂经历中走向“精致”的建构[J].小学数学教师，2015（3）.