深度学习理念下教学目标拓展的若干视角

【摘 要】基于深度学习理念，我们有必要重新审视教学目标的价值定位。本文以人教版数学的学习内容为载体，从目标设计与实施层面提出目标拓展的多元视角：意义理解、建立联系、综合应用、类比迁移、知识孕伏、思想方法等。试图通过目标研究，为教师提供发展性目标拟定的基本方向与思路，并最终促进“深度学习”理念向日常教学行为的转变。

【关键词】小学数学 教学目标 拓展 深度学习

深度学习，已成为当前教育研究的热点话题。深度学习，是以知识深度加工、意义建构和深度思维为主要特征，以理解、应用、分析、推理、综合、评价、创造等高层次认知活动为主要活动的学习。

从学习过程层面思考，深度学习的本质是一种主动的、探究式的、有意义的学习过程，其基本策略可以是：提供时间激活学生深度参与、设计高水平任务驱动学生深度思维、引导学生开展深究型对话互动等。

从学习结果层面思考，深度学习能够使学生将学到的知识进行迁移与应用，实现知识的深度加工、深刻理解以及长久保持，并实现“高认知能力”和“高阶思维”的发展。显然，深度学习的结果特征与教学目标直接相关。目标立意与目标视野，决定着教学的深度与走向，也必然决定了学习活动究竟是“虚假学习”“浅層学习”还是“深度学习”的基本属性。

因此，基于深度学习理念，我们有必要重新审视基于教材内容的目标定位，如何从基础性目标走向发展性目标？有哪些目标拓展的方向？本文以人教版数学教材为例，从目标设计与实施层面，提出目标拓展的多元视角：意义理解、建立联系、综合应用、类比迁移、知识孕伏、思想方法等。试图通过目标研究，为教师提供发展性目标拟定的基本思路与方向，并最终促进“深度学习”理念向日常教学行为的转变。

一、意义理解——概念、定律、性质、公式的意义理解与深度构建

意义理解是深度学习发生的重要标志。什么是意义理解？学习中，学生能否调动、激活知识经验，对学习内容加以解释，重新构建其意义，促进知识的学习从表层符号走向内在的逻辑形式和意义领域，促进意义与经验的对接，形成良好的知识结构，并能长久保持和灵活运用，是意义理解的重要标志。

审视当前的教材编写与教学过程，对于概念、性质、定律的学习，远没有达到“意义理解”的水平。以五年级下册“分数单位”的概念学习为例，教材用“把单位1平均分成若干份，表示其中一份的数，叫作分数单位。例如，的分数单位是”来进行定义。教学中，大多教师也仅停留于这一定义描述层面，分数单位的学习十分单薄。如何实现意义与经验的联结？如何提升概念的理解水平？我们可以对“分数单位”的教学目标做如下拓展设计。

目标1：沟通分数单位、小数单位和整数计数单位的共同本质。

目标2：运用分数单位，初步认识真分数、假分数（整数和带分数）。

目标3：借助分数单位，理解分数与小数的联系。

目标4：能运用分数单位，解释分数的大小比较、分数加减法、满几进1或退1当几（为假分数与整数、带分数互化做铺垫）等，感受分数单位的应用价值。

以“目标1：沟通分数单位、小数单位和整数计数单位的共同本质”为例，教师设计以下的学习材料与任务。

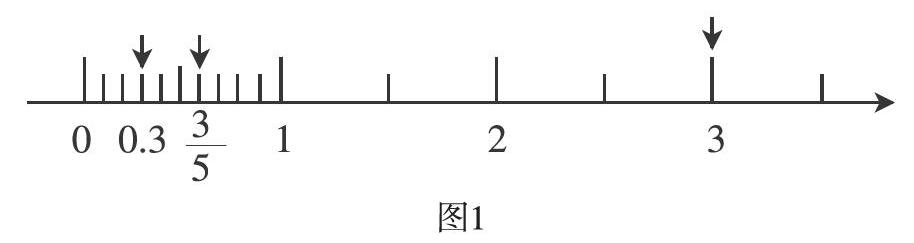
在数轴上找到0.3、、3的位置，并标出来。（如图1）

基于分数、小数、整数的意义，教师让学生在数轴上标出各数，并引导学生进行比较，思考它们有什么相同和不同之处。（如图2）

学生通过比较，发现0.3里面有3个0.1、里面有3个、3里面有3个1，都是3份，只是计数单位不同，计数单位分别是0.1、、1，分数中表示一份的数是分数的计数单位，也叫分数单位。这样，顺利将分数单位的概念理解纳入已有认知结构中，实现分数单位的意义建构和本质理解。

如何实现目标4？教师设计了这样的学习材料与任务：

请你利用分数墙，运用分数单位的知识，尝试进行研究：①借助分数单位，研究分数的大小比较，举例说明;②借助分数单位，研究分数加减法运算，举例说明;③借助分数单位，研究“满几进一”或“满几进几”，举例说明。

借助直观，以分数单位的意义理解为基础，学生自觉地将分数单位应用于分数大小比较、分数加减计算、假分数与带分数互化的学习中，为后续学习分数计算与分数互化积累经验。

为何做这样的目标延伸？我们说，概念学习的最高水平是概念应用。如果将概念的学习水平根据识记、理解、掌握、应用进行水平分类，如下表：

上表中，概念学习的水平自下而上递进，如若目标仅停留于识记层面，则属于“浅层学习”。显然，上述教学环节的展开，已将分数单位的概念理解提升至问题解决的应用水平，深度学习自然发生。就“分数单位”的学习而言，这样的目标视角，是大多数教师并未触及的。

二、建立联系——建立知识之间的本质联系，形成结构

“学习一个数学概念、原理、法则，如果在心理上能组织起适当的认知结构，使之成为个人内部知识的一部分，那么学生才会产生他们自己的数学理解。”如何用联系的观点贯穿于教学，关注数学知识之间、数学与其他学科之间的联系，使学生形成清晰、稳固的认知结构，既是深度学习的重要特征，也是教材目标拓展丰富的重要视角。

以“百分数”的教学为例，我们拟定下列目标：

目标1：感受百分数在实际生活中的广泛应用，能正确读写百分数。

目标2：数形结合理解百分数的意义，初步体会在用百分数表示部分与整体的关系时，它小于或等于100%;表示两个独立数量的关系时，它可以大于100%。

目标3：感受“一个数是另一个数的百分之几”与“一个数是另一个数的几分之几”“一个数是另一个数的几倍”以及“比”之间的联系，培养学生抽象、概括、分析、比较的能力。

显然，目标3便是对基础目标的提升与延展。教师可以在进行概念概括时，呈现新课展开中的五组材料：

苹果汁是果汁饮料的60%。甲车的速度是乙车的80%，也可以是105%。地球上海洋面积约是地球表面积的71%。今年旅游收入是去年同期的119.6%。两分球命中个数是投篮总数的40%。

再引导学生思考：能用学过的数来表示吗？怎样表示？学生自觉将“苹果汁是果汁饮料的60%”与“苹果汁是果汁饮料的”建立联系，将“今年旅游收入是去年同期的119.6%”与“今年旅游收入大约是去年同期的1.2倍”建立联系，将“地球上海洋面积约是地球表面积的71%”与“地球上海洋面积与地球表面积的比是71 ： 100”建立联系。由此，百分数、分数、倍、比都是“两个量的倍比关系”的“同”之比较，顺利将“一个数是另一个数的百分之几”纳入“一个数是另一个数的几分之几”和“一个数是另一个数的几倍”的已有认知结构中，形成概念系统，使学生明晰相关概念之间的逻辑关系，从而实现概念的融会贯通，促进学生对知识的整体性认识。

三、综合应用——跨越领域、多知识点的综合应用

浅表学习的基本特征是浅层次认知，难以在知识之间建立深度联结，而深度学习则是以深度理解、建立联系、高阶思维、问题解决为主要特征。因此，突破单一知识的学习，打通知识壁垒、跨越领域界限的綜合应用，是实现深度学习的重要途径。

我们以“负数”的教学为例，其核心目标是：

目标1：初步认识负数，能正确地读、写正数和负数;知道0既不是正数也不是负数。

目标2：理解正负数是表示一对相反意义的量。

目标3：基于正负数意义理解，解决综合性问题。

如何将目标3转化为教学行为，有效实现知识的深度理解与迁移应用？教师可在新课教学后，设计如下练习。

练习1：如图3，用数对表示点的位置。

材料与任务：用数对表示点A、点D的位置。

练习2：用数对表示图形的位置。

材料与任务：把按逆时针方向旋转记为“正”，按顺时针方向旋转记为“负”，现将图4中的三角形ABC绕点B先旋转+150?，再旋转-60?，得三角形A′BC′。请用数对表示出点A′和点C′的位置。

这样的教学，将负数的意义从“数与代数”领域向“图形几何”领域跨越，从“单一知识练习”向“多知识应用”迈进。练习1，突破“用数对表示位置”仅限于第一象限表达的局限，学生在拓宽数系的同时，也为后续学习坐标做了很好的知识孕伏。练习2中，“把按逆时针方向旋转记为‘正，按顺时针方向旋转记为‘负”，不仅深刻揭示了“标准”的相对性和自定义性，完成“旋转+150?” “ 旋转-60?”的操作任务，更是为“正负数表示一对相反意义的量”这一本质提供了更为宽阔的应用背景。这样，不仅没有削弱“负数”意义的理解，反而是对概念内涵的聚焦、概念外延的拓宽，其教育价值无论是对数概念的体系构建，还是对“相反意义”的本质理解，均有深刻的意义，更是为学生综合应用知识的能力培养提供了契机。

四、思想方法——文化浸润与思想渗透

深度学习指向的学习目标，还需“虚实有度”。所谓“实”，是指近期的、可测量的教学目标，即显性的知识技能目标;“虚”是指着眼长效的关于思想、关于方法、关于意识、关于习惯等层面的隐性目标。隐性目标无法一蹴而就，要在探索、发现概念、定律、公式和算法的过程中逐渐形成积淀。

以“圆的认识练习”目标设计为例：

目标1：巩固对圆的圆心、直径的认识，感受圆的美。

目标2：借助几何画板，使学生感受到圆与其他正多边形的关系，认识到圆的本质也是一个正无数边形，渗透极限思想。

显然，练习目标不仅有传统的知识目标，更是充分发掘了这一内容的文化内涵与思想价值。“圆的认识”起始课，学生已经认识了圆的特征、各部分名称等相关知识，然而这样就真的认识了圆的本质了吗？为此，教师在练习课中抛出这样的问题：同样是平面图形，圆为什么如此与众不同呢？由此展开观察、讨论，认识到圆的特质：有无数条相等的半径。再进一步深入：

师：在同一个平面图形中，具有这样相等线段的图形不是只有圆一个。瞧，正三角形，从中心出发，分别连接三个顶点，这三条线段相等。

（接着依次呈现正方形、正五边形、正六边形、正八边形、正十二边形，再整体呈现）

师：你发现了什么？

生：随着边数的增加，越来越像圆了。

师：但毕竟还不是圆，怎样能更接近一个圆？

生：边数再多一些，一定会更接近。

师：那你想看看正多少边形？

随后根据学生的意愿，教师用几何画板输入边数，学生看到了正二十四边形、正一百边形、正二百四十边形，甚至正一千边形。随着一声声的惊叹，学生切身感受到了随着边数的增加，图形确实越来越像圆了。

案例呈现的是将简单知识深入后的一种精彩，不仅巩固了有关圆的基础知识，同时，“理解感受圆与多边形的关系”“理解圆是一个正无数多边形之本质” “‘一中同长‘大方无隅的文化渗透”等目标随机诞生。圆与方的互相转化、有限与无限的对立统一、数学文化的无痕渗透，这难道不是对教材目标的极好拓展吗？

五、类比迁移——形成解决问题的策略经验

深度学习，同样指向于问题解决。解决问题的基本思路、基本程序、思维关键、数量关系、模型提炼等，是制订教学目标的重点。如果我们认识到教学目标所应具有的长远性和可持续性，那么，让学生拥有解决问题的策略与经验，类比迁移于其他陌生问题中，是目标设定的重要视点，比如：（1）多样化、多手段分析表征数量关系的经验;（2）正确确定标准，将较复杂或较隐蔽的数量关系转化为标准统一、关系清晰、利于表征的经验;（3）运用列表、转化、类比、画图、逆推、假设等策略解决问题的经验;（4）创造性解决问题的经验;等等。

以四年级下册“四边形内角和”的教学为例，目标怎样从“掌握四边形的内角和是360°”“探索多边形内角和的规律”等知识目标转向“转化”策略的经验积累，是教师需要重新加以思考的问题。

目标1：将一般四边形转化为长方形、正方形求得内角和，积累将一般问题转化为特殊问题的经验。

目标2：将四边形分成两个三角形或四个三角形，积累将未知问题转化为已知问题的经验。

有了这样的目标定位，教学展开将会聚焦于策略与经验，在解决新问题时，这些经验便可被激活，并实现迁移。

六、瞻前顾后——后续知识的合理孕伏

教师在拟定目标时，常常呈现出课时视角、目标短视的弊端。如何基于整体视野，既立足当下，又能为后续学习提供适度的知识孕伏与经验积累，是教学目标拟定时需要考虑的。例如，“平移旋转”教学怎样为“多边形的面积的推导”积累经验？“对称的初步认识”怎样为“对称的性质”做经验积淀？“面积的意义”怎样为“平行四边形的转化”埋下伏笔？等等。

以“三角形的认识”的教学为例，除“三角形的特性”“三角形底与高的认识”“三角形画高技能”等基础目标之外，如果从目标整体性角度考虑，我们还可以将其定位为单元起始课，“认识教学”为后续三角形的分类、三角形的内角和、三角形的三边关系等内容的学习作适度孕伏。

新课后，可设计如下材料与任务：

请在图5中以AB为底，画高为3厘米的三角形。

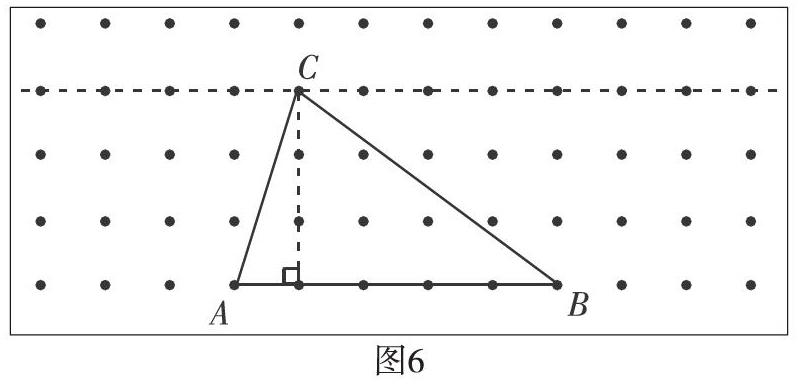
反馈任务一后，教师演示顶点C在虚线上的移动（如图6）。

思考：①你觉得可以画出多少个这样高为3厘米的三角形？

②在这些三角形中，你觉得哪几个比较特别？说说它的特点。

③选择三角形的边或角来进行观察，在C点移动的过程中，边或角有没有变化？有怎样的变化？

显然，教师的目标意图已不满足于三角形的浅层认识，目标由“可以画多少个高为3厘米的三角形”任务，指向“巩固高的意义”“熟练画高方法”的同时，为“同底等高的三角形形变面积不变”作孕伏;由“你觉得有哪些特别的三角形”任务，指向对各类特殊三角形的特征描述，为三角形的分类教学作相应孕伏;由“移动C点，观察边与角，发现什么”，为三角形的三边关系、三角形的内角和学习作孕伏。此案例，为教学目标拓展提供了“后续知识孕伏”的基本视角，同样值得教师们关注。

限于篇幅，以上仅从意义理解、建立联系、综合应用、思想方法、策略经验、后续孕伏等几个维度提出了课时目标丰富与拓展的方向，但这并不意味着是实现深度学习、实现目标拓展的全部视角，还需后续进一步探讨。

【参考文献】

[1]朱德江.“深度学习”的内涵意蕴与学导策略[J].教育视界，2018（10）.

[2]平國强.让学生拥有完整的解决问题经验[J]. 教学月刊，2019（9）.

[3]潘红娟. 用富有结构的材料改变教学的深度[J]. 教学月刊，2013（12）.

[4]郭华.深度学习与课堂教学改进[J].基础教育课程，2019（2）.

注：本研究系2019浙江省教研规划课题“小学数学课时目标的细化与丰富研究”（项目编号：G2019014）阶段性成果。