大数据分析在保险行业中的应用浅析
2021-07-09李欣然
李欣然 杨 杉
(四川大学锦城学院计算机与软件学院,四川 成都 611731)
一、引言
大数据技术的飞速发展引发了金融界的全面改革,其中保险行业也面临巨大的竞争压力,这种压力不仅是来源于外界信息的交互传播方面更是来源于行业内部的管理竞争、业务升级方面,因此保险公司将大数据分析运用在企业中的措施刻不容缓。从国内大数据技术与保险业结合发展的角度来看,在寿险及健康险领域,在逐渐普及基于大数据技术的用户管理及保险业务的应用。大数据应用的逐渐推广带来了较大的正面效应,实践也证明,大数据技术在保险业务中的应用对于促进保险公司效率提高、成本降低起到了积极作用。保险公司除了投保数据值得研究分析外,退保数据实则更能反映业务与客户的问题。基于以上背景,针对保险退保数据对其用户管理、险种业务等方面进行探索性研究。
二、研究思路
以四川人寿保险公司的退保数据进行分析,采用Excel、SPSS 数据分析工具,针对退保金额、保额、保费三者间的相关性建立回归方程,并将险种分类进行特征分析,包括退保机构、保额保费等。并围绕退保原因展开分析,比较用户性别、年龄段不同下是否会造成退保原因的选择差异,退保原因与退保金额的显著性关系。依次使用了频率分析、独立样本T 检验、线性回归分析等方法。
三、数据说明
1.数据来源
数据来源于四川人寿保险公司,覆盖了2008 全年的退保数据,时间跨度在1999 年至2008 年的投保保单,退保数据表中包含了保险机构、险种、总保费、保额、退保金额、退保原因、客户号、性别、年龄等9 个字段共167721 条数据,15.9M。
2.数据清洗
首先,进行数据预处理,筛选删除了对于研究退保险种特征以及退保用户基本画像无价值的数据、保留所需数据。其中使用了险种、退保金额、退保原因等字段的数据进行分析探索。通过观察家庭人口和教育程度字段发现其都进行了脱敏处理,字段值为空或值一样,对分析帮助和影响不大,因此删除此类数据。其次,修改格式设置,由于原数据的投保时间和退保时间整列的值没有正确显示,因此将这两列设置成日期格式。数据分类则通过统计汇总发现经济原因在退保原因当中占比最大超过了50%,而其余退保原因的占比很少,统一归为非经济原因,将退保原因分为经济原因和非经济原因。年龄段的分类中,由于用户信息中的年龄分布较散并且研究单个年龄的用户画像意义不大,因此分段设置。我国规定,18 岁以下的未成年人只享有保险受益者的权利无法自行进行投保,因此以18 岁为分界点,分为小于18 岁、18 岁~35 岁、36 岁~54 岁、55 岁~72岁以及72 岁以上5 个年龄段。险种分类中,按照险种的首字母进行了分类,直接分为S、L、B、Y、4、6 六大类险种。
四、险种特征以及用户基本画像
1.研究退保金额、总保费、与保额之间的线性关系
(1)各参数的相关性分析
由表1 可知:总保费、过去三年平均年收入、保额与退保金额之间的Sig 值都是小于0.01。退保金额的皮尔逊相关性一行的数据显示退保金额与总保费的数据是0.912**,与过去三年年收入的数据是0.083**,与保额的数据是0.375**。**代表相关性显著,相关性大于0.3 表示有较强相关性,因此选取总保费、保额与退保金额之间建立线性回归模型。
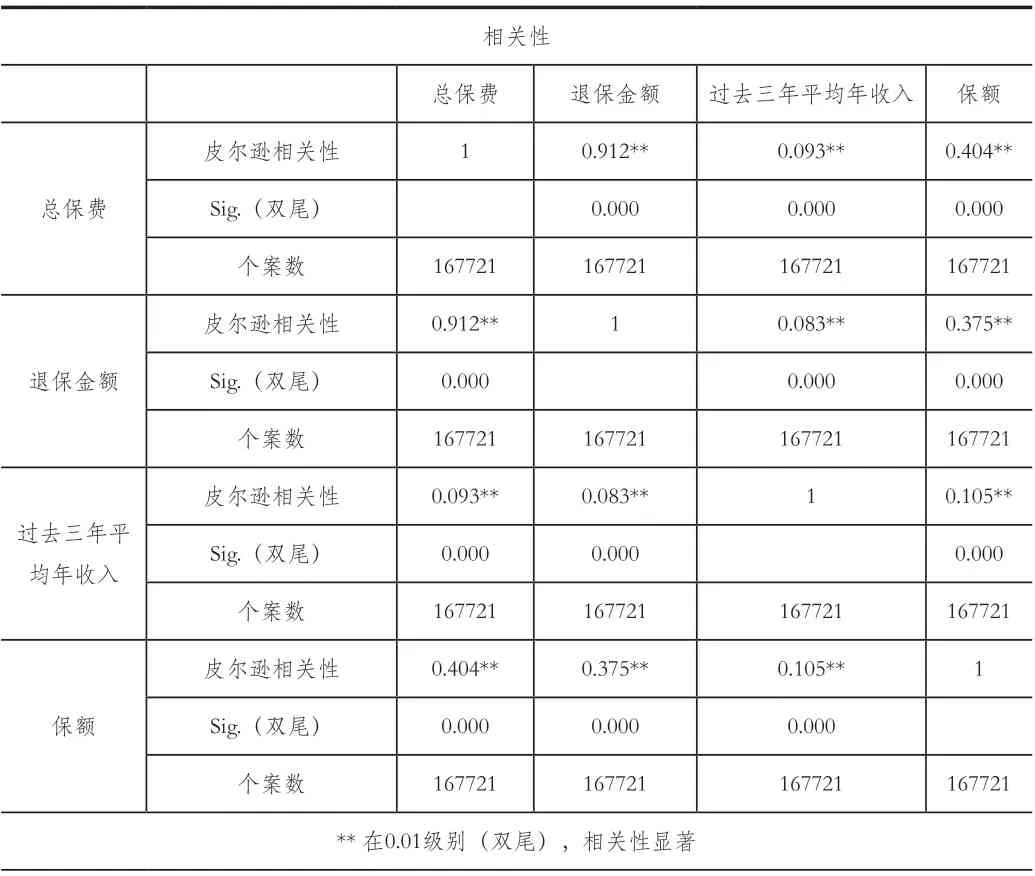
表1 总保费、退保金额、保额三者相关性比较
(2)建立线性回归模型
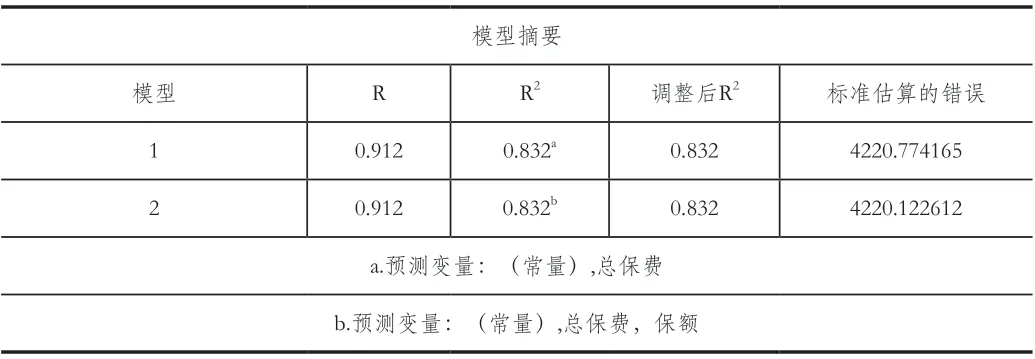
表2 总保费、保额、退保金额的线性回归模型
选取总保费、保额与退保金额之间建立线性回归模型。利用步进方法分别得出2 个模型。模型一:退保金额与总保费的模型;模型二:退保金额与总保费以及保额的模型;在表格中模型的R2的数值都为0.832,R2接近于1 说明模型拟合度较好,因此2 个模型的变量与因变量的总体存在着较强相关性。
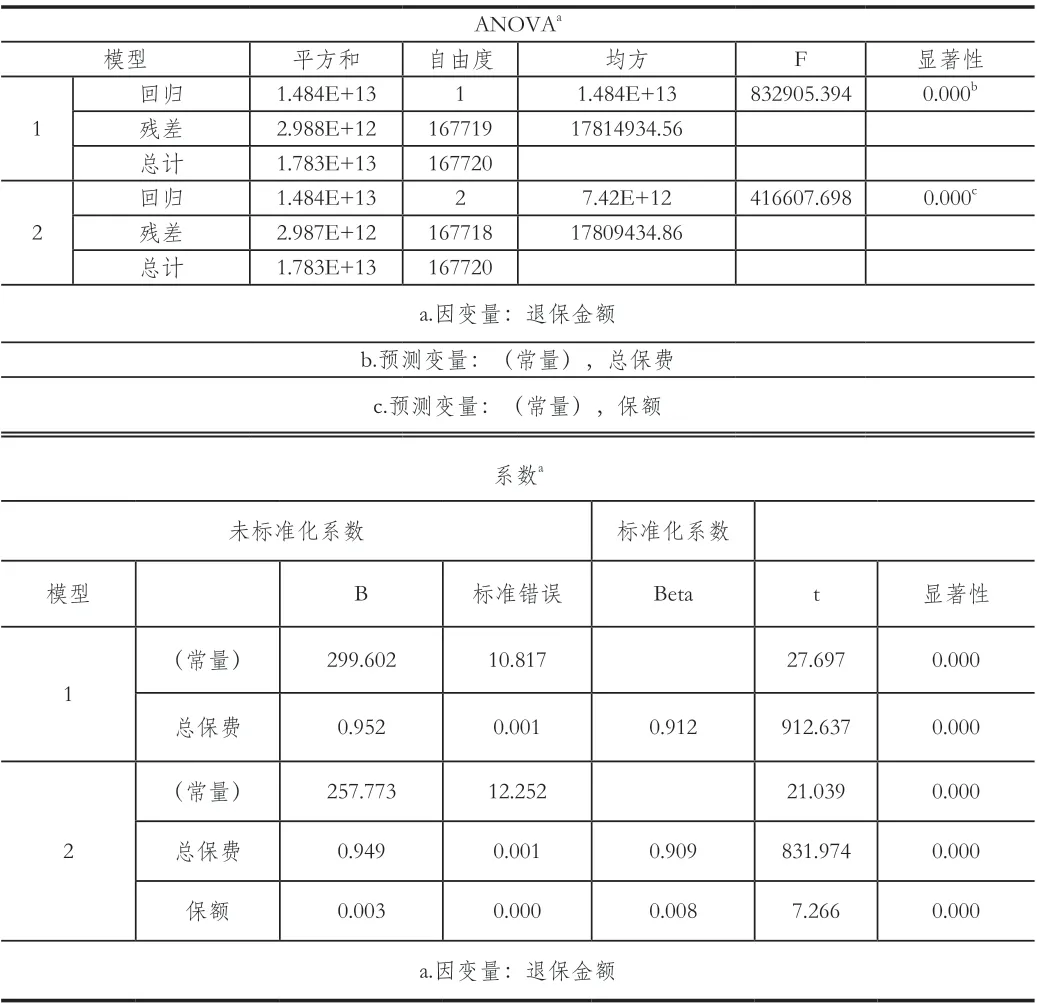
表3 线性回归模型的方差分析、线性回归方差的参数系数值
由表3 可知:ANOVA^a对模型进行了方差分析,从模型的显著性可以看出数据都是小于0.01 的,进而模型的显著性较强,由此说明模型是有效的,可以借此去判断和计算相关数值,总保费、保额与退保金额的线性回归模型可通过第2 个模型去探究具体线性关系。从上述的系数^a 表中得出总保费、保额的系数分别是0.949、0.003,则相关线性回归方程是:退保金额=0.949×总保费+0.003×保额+257.773
2.不同险种下的退保特征画像
(1)险种分类
观察数据的险种信息可知,按险种的首字母作为分类依据,共分为六大类险种。因为在SPSS 分析工具中,以险种作为分类字段需为数值性的数据,因此将B、L、S、Y 字母分别替换为7、8、9、0 四个数字。研究每一个具体险种的退保特征不具有现实意义且适用范围不广,因此逐类分析研究,使用频率分析功能研究每类险种退保率最高的机构、退保险种的特征包含保额与保费、退保金额和总体退保数据的分布趋势。
(2)主要险种的退保特征数据可视化展示
S 类险种有252615 条退保个案,占比90.9%;Y 类险种有8976 条退保个案,占比5.3%。在Excel 中使用筛选统计功能,统计出其余险种占比依次为1.4%、1.6%、0.5%、<0.1%。主要选取S、Y 两种险种展开退保特征画像分析。
Y 类险种中,易被退保的机构513804,容易退保的保险有保额为10000 总保费为1000 的特征,此类保险的用户黏性较差。Y 类险种,机构、保额、总保费和退保金额都是右偏分布,位于均值右侧。除机构为扁平分布,离均值较稀疏外,其余参数尖峰分布,集中于均值附近。S 类险种中,易被退保的机构是513803,容易退保的保险有保额为10000 总保费为590 的特征,说明此类保险用户满意度不高。S 类险种,机构、保额、总保费和退保金额都是右偏分布,分布与均值右侧。除了机构为扁平分布,离均值较稀疏外,其余参数尖峰分布,聚集与均值两侧。
因此在保险险种中513803、513804 为主要的被退保机构,其中S、Y 险种退保率最高。被退保的险种中特征为保额10000总保费1000,客户的忠诚度最低。
3.探究退保原因与退保金额是否造成显著影响、性别和年龄段与退保原因的分布
退保数据中除了关注具体的退保金额,还需关注客户退保的根本原因。围绕退保原因展开分析,分别分析与退保金额、客户性别、年龄之间是否有关联产生影响,目的在于推测高退保风险的客户人群画像以及退保原因。为保险险种业务的不断完善和改进提供思路。
通过对退保原因的初步观察发现,退保原因中经济原因的占比为77%,是主要的退保原因而其余退保原因的占比共占23%,因此在退保原因的分类中,以经济原因作为分类依据,并利用Excel 中的替换功能把退保原因分为经济原因和非经济原因后替换成数字1、2,导入SPSS 当中完成独立样本t 检验,把退保金额方法检验变量,把分组变量变成退保原因,并且定义组1,组2,组1 是经济效益,组2 是其他余下的退保原因。选取簇形图构建图形,类别为性别、聚类定义为退保原因。
将客户的年龄分为18 岁以下、18 岁~3 5岁、36 岁~54岁、55 岁~72 岁、大于72 岁及以上。对数据进行整理、归类,最后根据数据归纳总结出高退保风险的客户基本画像。
四、分析过程

表4 独立样本检验统计值
如表4 所示,分析退保金额之间是否因退保原因而产生差异性得出结果,从方差的齐次性检验得出:因为其显著性差异的数据值小于0.05 拒绝原假设,方差不具有齐次性。通过方差的齐次性看到Sig.值<0.05,说明退保金额之间有一定差异性,不同的退保原因导致的退保金额的均值是不一样的。均值差异为551,置信区间的下限值是443 上限值是669,所以均值的范围95%是在这个范围之内的,可信度高。
男性在退保原因上选择经济原因的占多数,其后依次为正常退保、险种不理想、失效退保,而其余的几项退保原因的占比更小,而在女性的数据分布同男性相似,因此在退保原因的选择上男女的差异不大。
经济原因仍是最主要的退保原因,在年龄阶段中占多数的退保原因的年龄段有18 岁~35 岁,36 岁~54 岁,55 岁~72岁,其余年龄段比例几乎忽略不计。人数占比最多的是36 岁~54岁年龄段,因此其为高退保年龄段的区间。
五、结论及建议
1.结论
总保费、保额与退保金额之间存在显著相关关系,线性关系方程是退保金额=0.949×总保费+0.003×保额+257.773。513803、513804 为主要的被退保机构,其中S 与Y 的险种被退保率最高,被退保的险种具体特征为保额10000 总保费1000。退保原因的差异导致用户在退保金额上的均值有差异,性别上差异不大。36 岁~54 岁为高退保风险人群,经济原因是占主要的退保原因。
2.建议
对于较高保额、保费的业务应给予更多的关注,此类保险业务的退保金额通常较高,会引起较大数据波动。513803、513804 的保险机构需要改进S 和Y 险种,保额为10000 和总保费为1000 的险种需要注意其保险比例设置,比例存在不妥当就会造成客户忠诚度低,退保人数多的现象。
经济原因是最主要的退保原因,36 岁~54 岁是最高退保风险的用户年龄区域。因此保险公司向用户推荐业务时要结合用户年龄和经济情况来进行推荐,在平日的用户管理时,重点关注这个年龄段的用户,预防并做好其退保措施。
