大跨越输电塔线体系断线响应分析

2021-07-08张健琦张德凯邓洪洲

山东电力技术 2021年6期

张健琦，张德凯，邓洪洲

（同济大学，上海 200092）

0 引言

强风、雷电、覆冰、电线的疲劳均可以导致线路发生断线事故，造成供电中断、断线倒塔等事件［1］。输电线路工程是电力系统建设的重要环节［2］，自立式输电塔属于柔性结构［3］，即便断线事故并不是一个大概率事件，但是一旦发生，不仅会造成电气设备的损坏，严重时甚至会造成输电塔连续倒塌。对于大跨度的输电塔线体系来说，这种破坏会造成整个输电塔线体系的瘫痪和巨大的经济损失。

断线事故发生时会产生极大的不平衡张力，对输电塔线体系产生巨大的冲击作用，使输电塔产生较大的内力和位移响应，对于大跨度输电塔线体系来说，这种冲击作用带来的危害更加明显。但我国目前的架空输电线路设计规范和标准［4］还未考虑断线的动力冲击作用，这是存在安全隐患的。

国内外学者在断线方面的研究始于20 世纪70年代，Mozer 等［5］通过简化物理模型提出了分析输电塔线体系不平衡张力的具体步骤；John 编制了计算程序，用于分析一根或多根导（地）线断裂时对输电塔线体系的动力冲击［6］；夏正春等［7］采用等效弹簧替代输电塔用以获得输电塔线体系的动态响应；李黎等［8］借助了ANSYS/LS-DYNA，采用非线性动力有限元的方法，研究了输电塔线体系单根导线断线响应和初张力、档距、绝缘子等参数的关系。上述研究运用了非线性动力有限元分析了断线工况下输电塔线体系的动态响应，但对于耐张段的长短影响，导线、地线不同断线工况的差异，以及断线工况下对于输电塔构件内力影响缺少研究，且未与静力计算的规范结果进行比较。

借助有限元程序ANSYS，采用非线性隐式动力分析有限元的方法，研究大跨越输电塔线体系单根导（地）线断线对输电塔线体系的冲击响应，研究耐张段的长短影响，导线、地线不同断线工况，断线工况下对于输电塔构件内力影响，将动力分析的结果与静力计算的规范结果进行比较，以便为今后线路设计提供参考。

1 理论分析与假定

1.1 基本假定

研究大跨越输电塔线体系在断线下的响应，有限元模型有如下假定：

1）考虑几何非线性，材料符合胡克定律；

2）导（地）线采用多段只能受拉不能受压的两节点直线杆单元模拟，地线夹具、绝缘子串采用两节点的直线杆单元模拟；

3）导（地）线单元之间、导线与绝缘子串、地线与地线夹具之间均采用理想铰接；

4）断线点处于绝缘子与导线或地线夹具与地线连接处；

5）按照等面积等刚度原则，将分裂导线等效为一根整体导线，断裂时认为子导线同时断裂。

1.2 理论分析

1）输电塔线体系在重力作用下处于平衡状态，此时导（地）线存在张力，采用非线性静力分析，基本方程为

式中：d为节点位移向量，会随着时间t的变化而变化；K为结构刚度矩阵，由于几何大变形呈非线性，刚度矩阵随着节点位移向量d的变化而变化；W为自重等效节点荷载向量，由于断裂的导（地）线在重力的作用下跌落，存在几何大变形，会随着时间t的变化而变化。

2）在初始平衡的条件下，导（地）线断线内力瞬间移除，导（地）线释放应变势能，对体系产生激励，使体系在此激励下做阻尼自由振动，采用非线性动力分析，基本方程为

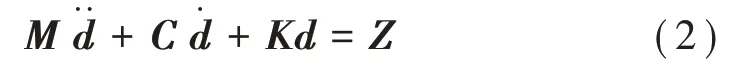
3）随后，断裂的导（地）线在重力的作用下跌落，使体系在重力的作用下做有阻尼的受迫振动，采用非线性动力分析，基本方程为：

2 输电塔线体系的有限元建模

该大跨越输电塔跨越塔高266 m，呼高244 m，塔体形状为“干”字型，基底根开为51.64 m，跨越塔为双回路三角排列；锚塔高度66 m，呼高34 m，单回路垂直排列。塔线体系的有限元模型如图1 所示，定义X向为塔线体系垂直导线方向，Y向为塔线体系顺导线方向，Z向为输电塔竖直方向。输电塔主跨越段跨度为2 500 m，弧垂为214 m，两耐张段的跨距为790 m 和557 m，弧垂分别为22.7 m 和11.9 m。地线夹具与导线绝缘子串长度分别为1.0 m 和7.8 m，导线为三分裂JLHA4/G5A-500/230 钢芯铝合金绞线，地线为光缆OPGW-308，48 芯。导线及地线物理力学参数如表1所示。

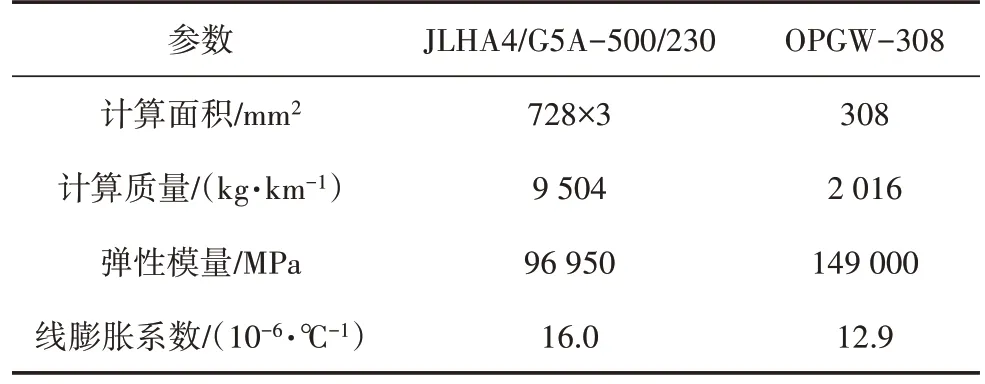
表1 导线及地线参数

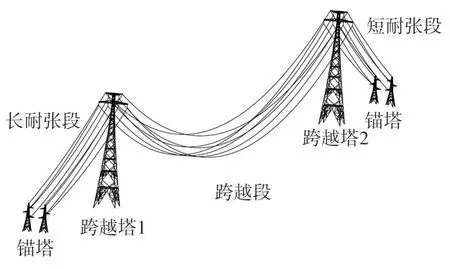
图1 输电塔线体系的有限元模型

建立输电塔线体系的有限元模型，模型包括4个锚塔、2 个跨越塔、导线和地线、绝缘子等，为简化计算，将爬梯、节点板、间隔棒、阻尼线等简化成附加质量作用在输电塔线体系上；塔下的基础刚度很大，在建模时将4 个塔脚的自由度全部约束；导（地）线所受到的重力荷载沿导（地）线的弧长均匀分布，此时导（地）线的形状为悬链线［9］，当垂度小于1/9 时，悬链线和抛物线差别很小，二者误差可为工程所接受，故导（地）线的形状模型采用抛物线。

3 导（地）线断线的有限元模拟

输电塔线体系的断线模拟采用如下的步骤：

1）输电塔线体系在重力的作用下保持平衡，并使各个构件产生内力；

2）突然断线采用有限元中的生死单元法来模拟，导（地）线的断裂是突然发生的，断线在极短的时间内发生，断线时间认为是10-8s，断线后认为断线处的导（地）线张力瞬间线性移除；

3）在断线时程分析中，荷载步步长为0.01 s，采用自动时间步长，最小子步长为10-8s，时间长度取20 s；

4）输电塔线体系采用瑞利阻尼，阻尼比取0.02［10］，瑞利阻尼矩阵计算公式为

式中：ɑ为Alpha 阻尼，也称阻尼质量系数；β为Beta阻尼，也称刚度阻尼系数［11］。

4 输电塔线体系的断线响应分析

研究在断一根导（地）线的情况下输电塔线体系的断线响应特性，断线点处于跨越段边缘时，最为不利［8，12-13］，限于篇幅，只研究断线点处于跨越段边缘的工况。由于该体系顺导线方向对称，且两个耐张段的距离不等，故共有8 种工况，为方便叙述，将各种工况进行编号。先对跨越塔进行编号，沿Y 轴正方向，将跨越塔分为跨越塔1 和跨越塔2，导线与地线位置及编号如图2 所示。以编号“导线2-3”为例，“导线”表示断线为导线，2 表示断点在跨越塔2 处，3表示断点在导线3 上，故若仅断一根线，共有“导线1-1”“导线1-2”“导线1-3”“地线1”“导线2-1”“导线2-2”“导线2-3”“地线2”8种工况。对绝缘子及地线夹具进行编号，与断线工况类似，以“绝缘子2-1”为例，2 表示在跨越塔2 上的绝缘子，1 表示与导线1 连接的绝缘子。断线位置如图3所示。

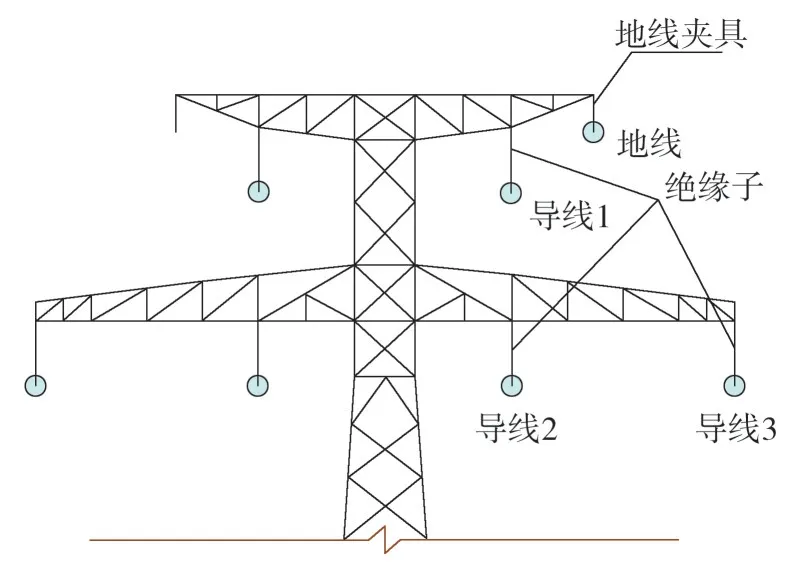
图2 导线与地线位置和编号

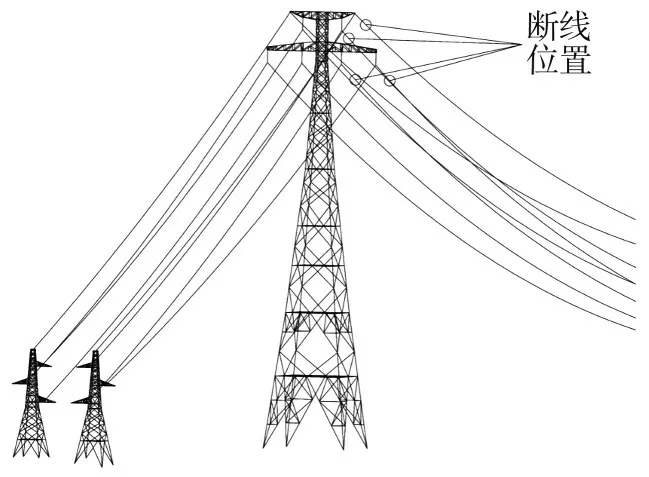
图3 输电塔线体系局部视图

4.1 位移响应分析

由于不同工况下的位移响应类似，限于篇幅，仅列举出导线1-1、导线2-1 和地线1、地线2 这4 种工况下绝缘子（地线夹具）下端与导线（地线）相连接点的三向位移图，如图4 所示。在导线跌落的过程中，与断线相连的跨越塔的绝缘子发生了大幅摆动，由初始时刻的竖直位置变成了接近水平的倾斜位置，而后在一个固定值附近摆动。

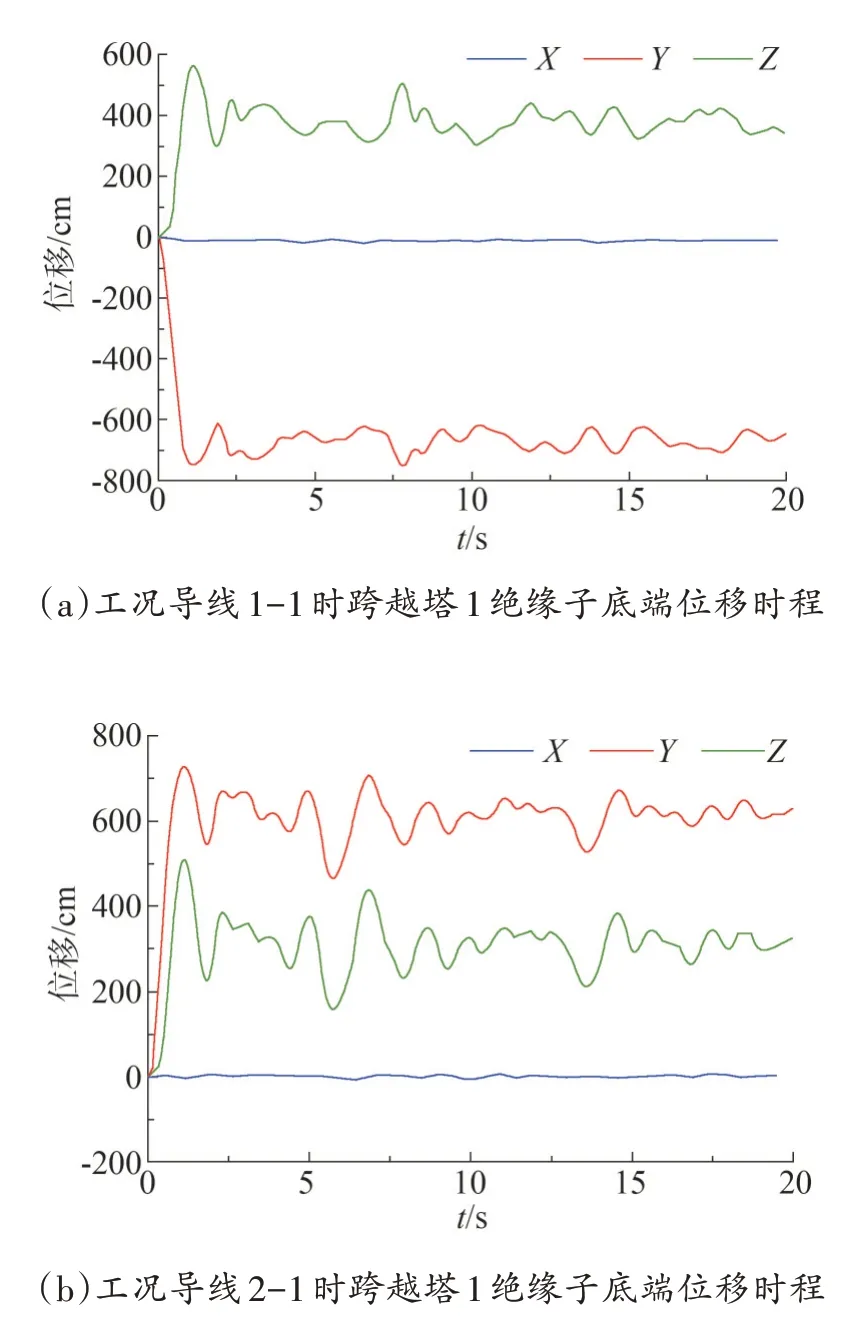
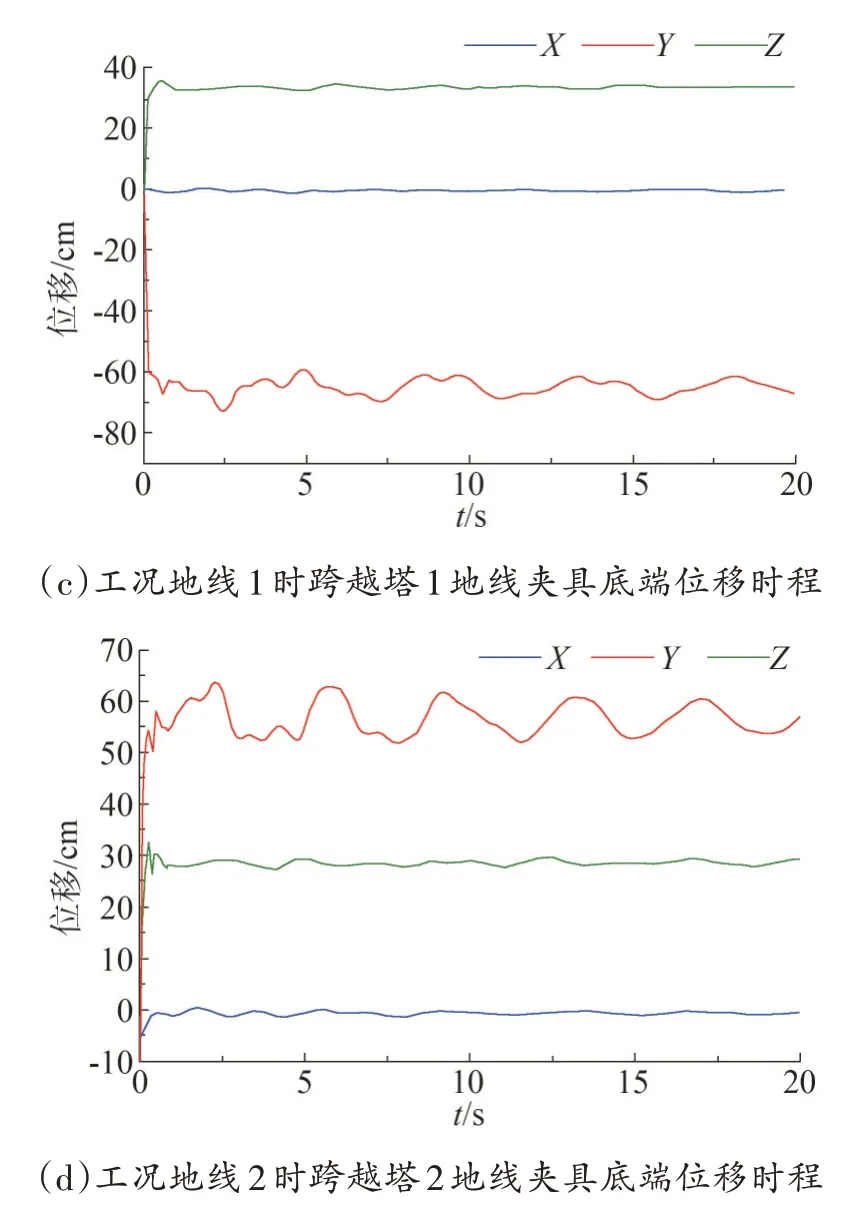
图4 不同工况下绝缘子及地线夹具底端三向位移时程

当断线点在跨越塔1 上的导线上时，绝缘子在高度方向（Z方向）向上摆动，最大摆幅约为5.6 m，在顺导线方向（Y方向）做远离跨越塔的运动，最大摆幅约为7.8 m，Y方向和Z方向的最大摆幅几乎同时出现，出现时间大概为1.2 s，在大概4 s 后，绝缘子的摆动变得缓慢。

当断线点在跨越塔1 的地线上时（即工况地线1），由于地线夹具的长度较小，3 个方向的位移尺度都远小于绝缘子，地线夹具在高度方向（Z方向）上向上摆动，最大摆幅约为37 cm，在达到最大摆幅后，Z方向的位移达到稳定，在顺导线方向（Y方向）做远离跨越塔的运动，最大摆幅约为76 cm，Y方向的最大摆幅时间为2.5 s，略微滞后于Z方向的最大摆幅时间0.3 s；当断线点在跨越塔2 的地线上时（即工况地线2），上述规律依然成立，且发生最大摆幅的时间一致，但数值上略小于地线1 工况，Y方向的最大摆幅为64 cm，Z方向的最大摆幅为33 cm。

综上，可以发现，断线对靠近长耐张段的位移响应较大。虽然输电塔线体系不存在沿X方向（垂直导线方向）的扰动，但断线处与绝缘子点还是在X方向存在着微小的振动，这是由于断线使跨越塔的受力不平衡，使跨越塔产生了绕Z方向的扭转。

4.2 轴力响应分析

4.2.1 绝缘子轴力响应分析

在跨越段的每根导线左右两端连接着2 个绝缘子，在一侧发生断线时，对连接该导线两端的绝缘子都存在着冲击作用，由于各种工况下的时程图相类似，仅给出工况导线1-1、导线2-1 下2 个绝缘子的轴力时程，如图5所示。

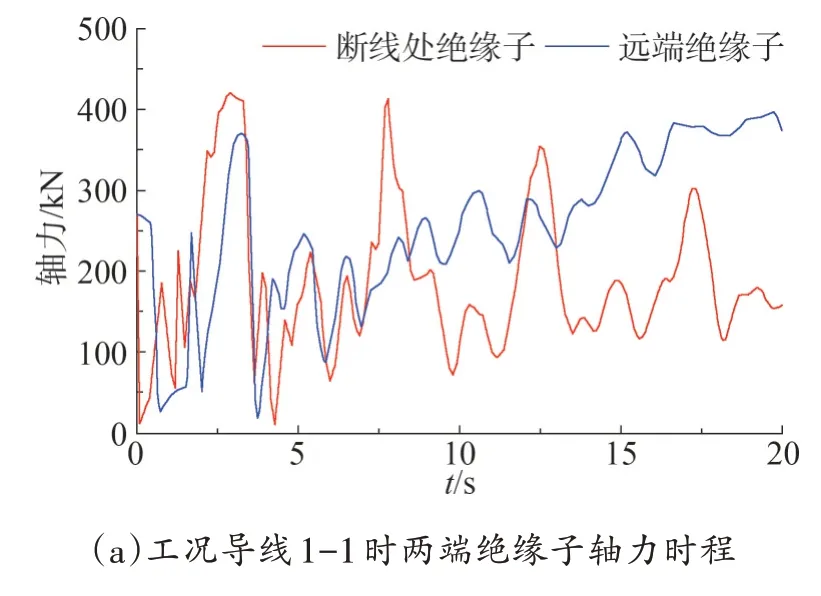
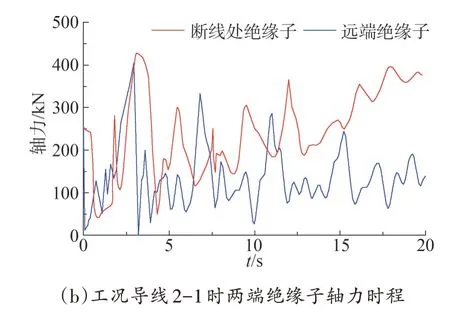
图5 不同工况下绝缘子轴力时程

由图5 可观察到，两个轴力时程曲线有明显的波动状态，且在计算的工况下，断线处的绝缘子在断线后的0.1 s时间内轴力先迅速减小，而后逐渐变大，在接近t=2.5 s 的时候达到极大值，时间滞后于Y、Z方向位移的峰值，而后随着时间的变化峰值逐渐衰减；断线远端的绝缘子在断线后的前0.3 s 轴力保持不变，后迅速减小到t=1 s 时刻，之后逐渐增大到第一个峰值后逐渐减小，在t=4.3 s到达低点，而后呈周期性地逐渐增大，甚至会超过第一个峰值。断线处的绝缘子随着时间的变化峰值逐渐衰减是由于阻尼的作用；断线远端的绝缘子在断线后的前0.3 s 轴力保持不变是由于断线的冲击作用传递到远端的输电塔需要一定的时间，而断线远端的绝缘子后期呈周期性逐渐增大是由于导线的掉落落重力牵拉以及阻尼的共同作用。

引入动力系数η［14-15］

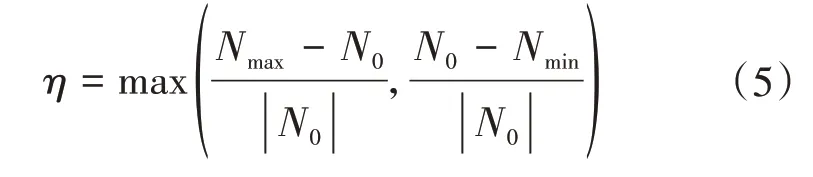
式中：N0为只受重力作用下杆件的轴力值；Nmax为杆件在断线工况下的轴力最大值；Nmin为杆件在断线工况下的轴力最小值。

不同工况下绝缘子的动力系数η如表2 所示。可以发现，在相同工况下，靠近长耐张段的绝缘子最大力要略大于靠近短耐张段的绝缘子；相同工况下，断线处的绝缘子动力系数要略大于远端绝缘子的动力系数；对于同一绝缘子，在靠近该绝缘子处断线的动力系数较大。

表2 不同工况下绝缘子的动力冲击系数η

4.2.2 地线夹具轴力响应分析

由于地线1 和地线2 两种工况时地线夹具的轴力时程相类似，以工况地线1 为例，给出地线夹具的轴力时程如图6 所示。可观察到地线夹具轴力时程规律与绝缘子相类似；同时可以发现，重力对远端的地线夹具作用相当大，会超出第一个峰值。

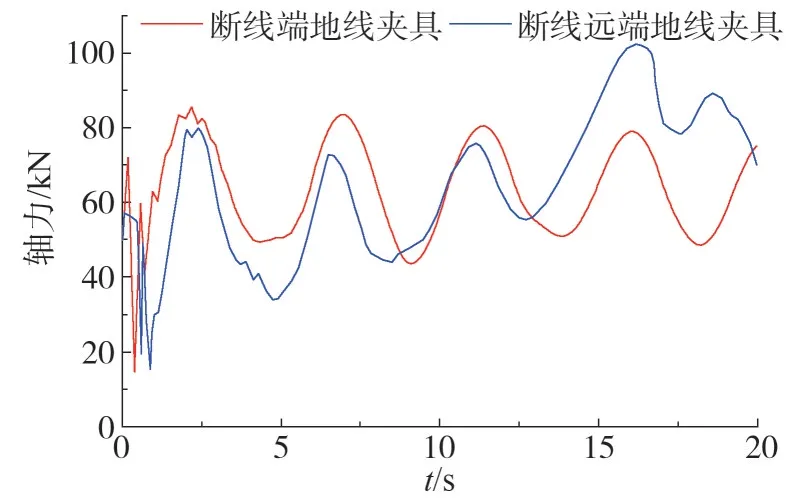
图6 地线夹具轴力时程

不同工况下地线夹具的动力系数η如表3所示。可以观察到地线夹具的动力系数会小于绝缘子的动力系数，且与绝缘子不同，断线远端的地线夹具的动力冲击要大于断线处的地线夹具，对于同一地线夹具在远离该处断线受到的冲击作用越大。

表3 不同工况下地线夹具的动力冲击系数η

4.2.3 跨越塔构件轴力响应分析

对于大跨越输电塔线体系，杆件的轴力起主要的控制作用。因跨越塔杆件数量过多，限于篇幅，仅对工况导线1-1 下的部分杆件进行分析。各主要杆件单元位置如图7 所示，其中2、5、123、124、263、264、553、562 号单元为远离跨越段的主材单元，8、11、125、126、265、266、569、578号单元为靠近跨越段的主材单元。塔身主材的动力冲击系数η如表4 所示，由此可知，断线对输电塔的冲击系数随着塔高的升高逐渐变大，且对于塔身主材而言，远离跨越段的主材受到断线的动力冲击更明显。以横隔材287 号和斜材329 号为例，其中横隔材287 号位于跨越塔1标高136.7 m 的横隔面处，如图8 所示。二者的轴力时程如图9和图10所示。

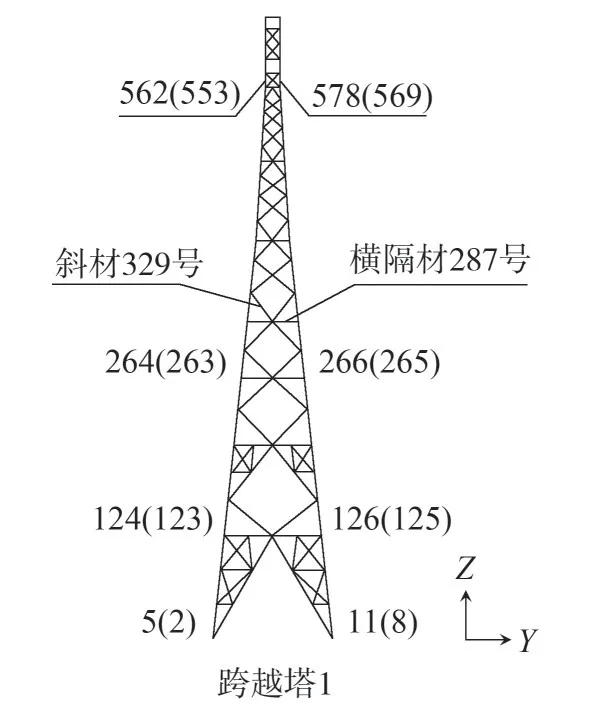
图7 主要杆件单元位置

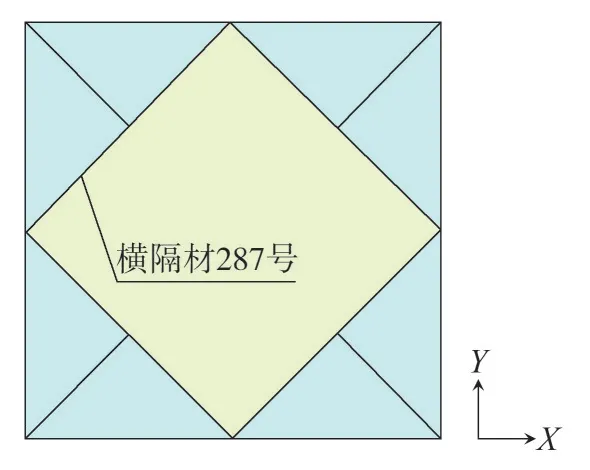
图8 横隔材287号位置

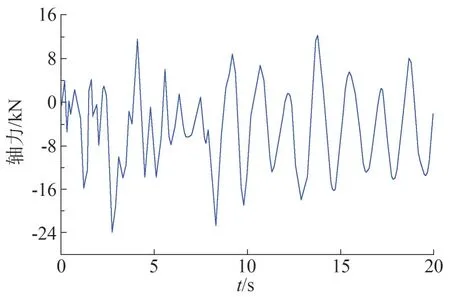
图9 横隔材287号轴力时程

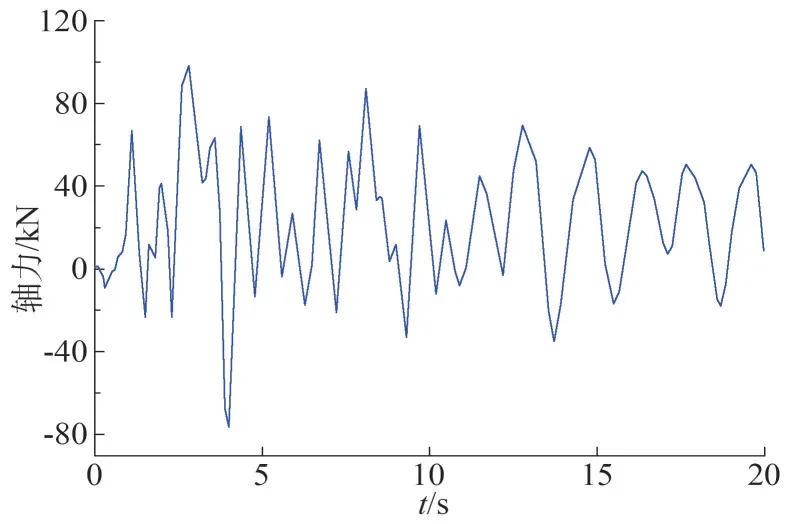
图10 斜材329号轴力时程

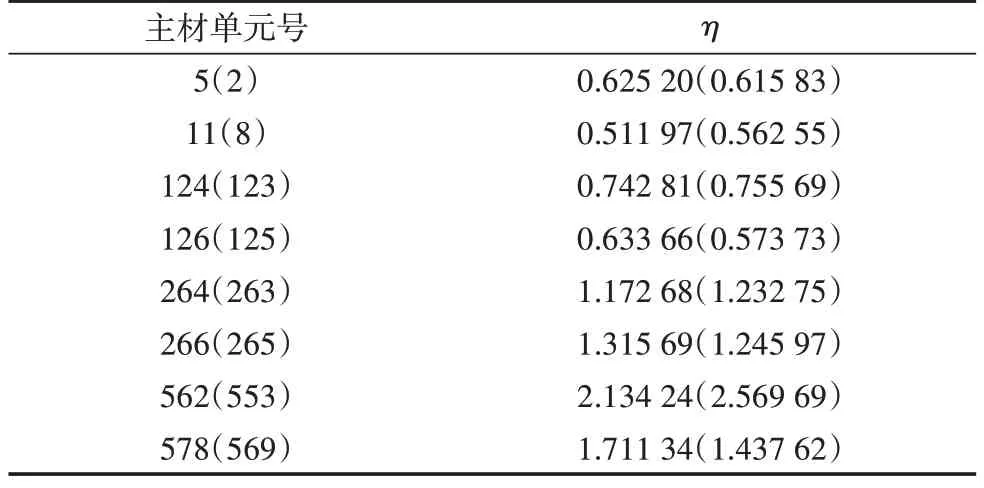
表4 塔身主材的动力冲击系数η

可以看出横隔材和斜材在重力荷载下基本不受力，但是在断线下，会受到较大的冲击作用，且会存在较大的压力，会使斜材及横隔材出现受压失稳，在设计时应予以考虑，避免出现受压失稳破坏。

5 断线张力结果与规范方法比较

输电线由于断线，在断线档的相邻档输电线具有的水平张力，即为输电线的断线张力［16］。经动力分析计算，可以得出最大的导线断线张力为386 kN，最大的地线张力为79.7 kN。

根据DL/T 5485—2013《110 kV～750 kV 架空输电线路大跨越设计技术规程》的要求，各类杆塔在断线情况下的断线张力的不平衡张力应按照静态荷载考虑［17］。导线断线张力（或分裂导线纵向不平衡张力）的取值为最大使用张力的60%，即导线的断线张力为373 kN，地线断线张力的取值为最大使用张力的100%，即地线的断线张力为95.76 kN，计算可知，导线断线动力分析计算结果要比规范的静力计算结果大3.5%，地线断线计算结果比规范小。