基于知识蒸馏的锅炉飞灰含碳量预测研究
2021-07-08杨兴森王海超杨子江
路 宽,杨兴森,王海超,刘 科,杨子江
(1.国网山东省电力公司电力科学研究院,山东 济南 250003;2.山东科技大学电气与自动化工程学院,山东 青岛 266590)
0 引言
飞灰含碳量是影响锅炉燃烧热效率的主要因素[1-3]。飞灰含碳量过高,会造成机械不完全燃烧热损失增大,燃烧效率下降,锅炉受热面磨损、结焦积灰,从而缩短使用寿命,严重时会出现锅炉灭火、机组停运等事故。因此,飞灰含碳量的实时准确预测对于火电厂机组的安全运行、节能减排、经济效益等有着重要意义。
目前,飞灰含碳量的预测方法主要是通过采集易于检测且与飞灰含碳量密切相关的辅助变量,研究其与飞灰含碳量之间的关系,然后运用统计分析、机器学习等方法建立可靠的数学模型[4]。王芳等[5]提出利用随机森林的变量选择方法筛选最优变量,将最优变量完成随机森林建模训练,进而实现了飞灰含碳量的预测;王春林等[6-7]应用支持向量机算法建立了大型四角切圆燃烧锅炉飞灰含碳量特性的模型;崔锐等[8]运用反向传播(Back Propagation,BP)神经网络进行飞灰含碳量预测,并结合LM(Levenberg⁃Marquardt,LM)优化算法进行网络训练;赵新木等[9]基于BP 神经网络建立了飞灰含碳量预测模型,并进行了单因素影响因素分析;冯旭刚等[10]提出了基于遗传神经网络敏感度分析的飞灰含碳量测量方法。
上述文献中关于飞灰含碳量预测的方法都是以影响参数和飞灰含碳量的采样周期一致为前提的。但现实中,受飞灰实时采样装置维护成本高、准确度低或没有安装等因素影响,大部分电厂的飞灰含碳量主要是通过燃烧失重法[11]来实现测量。由于燃烧失重法存在中间环节多、测量结果时间滞后等问题,因此获得飞灰含碳量样本的采样周期必然与锅炉运行参数等实时指标的采样周期存在偏差。前者的采样是以小时级为单位,而后者的采样周期往往以分钟级为单位。
因此,为了能够既保证实际飞灰测量的准确度,又充分利用锅炉运行的大数据信息以提高飞灰含碳量预测模型的准确度,提出一种基于知识蒸馏框架的火电厂锅炉飞灰含碳量预测模型,目的是在模型输入值采样周期和实际飞灰含碳量采样周期存在差异时,给出准确的分钟级飞灰含碳量预测结果。该框架由Teacher 模型和Student 模型两部分组成,其中:Teacher 模型通过前馈神经网络模型弥补锅炉实时运行参数和飞灰实际测量值的采样周期差异,完成对实时飞灰含碳量的数值模拟;Student 模型则通过随机森林模型完成对飞灰含碳量的实时预测。模型应用于山东省内某电厂在运机组的飞灰含碳量预测,取得了良好的效果。
1 影响因素分析与数据预处理
影响飞灰含碳量的因素主要分为设备运行因素和煤质因素两大类。机组运行因素主要包括发电机组有功功率、选择性催化还原(Selective Catalytic Reduction,SCR)进口烟气氧量、一次风机风量、二次风机风量等25 个指标;煤质因素主要包括空气干燥基水分、灰分等7个指标。表1给出了建模过程中所使用的主要变量名称。其中:锅炉运行指标的采样频率为1条/min,煤质和实际飞灰含碳量的采样频率都为1 条/6 h。这里,考虑到煤质的变化周期较长,因此认为煤质数据在每6 h的周期内不发生变化,这样就可以把煤质数据分解到每分钟里,与运行数据保持一致。

表1 模型主要参数
通过山东省网源监督服务技术平台提取了山东省某电厂的机组运行和煤质数据作为建模的数据源。由于数据中存在缺失值、异常值等,因此建立了数据预处理流程以提升数据质量,如图1所示。
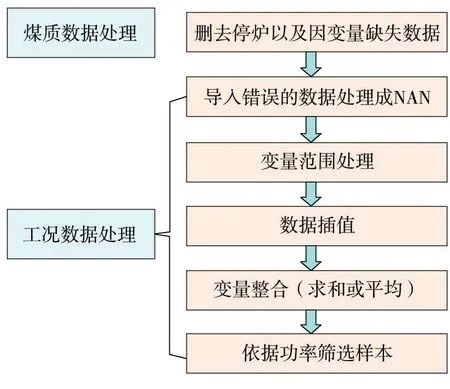
图1 飞灰含碳量数据预处理流程
2 Teacher⁃Student模型
2.1 Teacher模型
在机器学习和认知科学领域,人工神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型,用于对函数进行估计或近似[12]。神经网络由大量的人工神经元联结进行计算,其能在综合外界信息的基础上改变内部结构,是一种自适应系统。这里的Teacher 模型采用了多层前馈神经网络,学习从自变量到因变量的映射。模型为含4 层神经网络,输入变量维度为32 维,两个隐含层的神经元个数分别为512 和256,最终输出层为含碳量的预测,如图2所示。
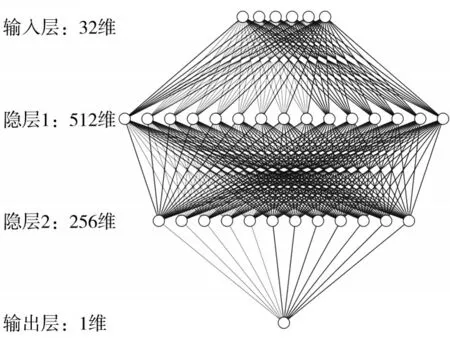
图2 Teacher模型网络结构
选取ReLU 函数[13](Rectified Linear Unit,ReLU)作为Teacher模型的激活函数,计算公式为
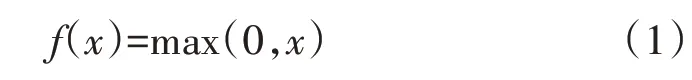
2.2 Student模型
Student 模型采用了随机森林算法Xgboost[14]。Xgboost 每一轮训练一棵树,使得损失函数能够极小化。其损失函数不仅衡量了模型的拟合误差,还增加了正则化项,即对每棵树复杂度的惩罚项,来防止过拟合。损失函数的计算公式为
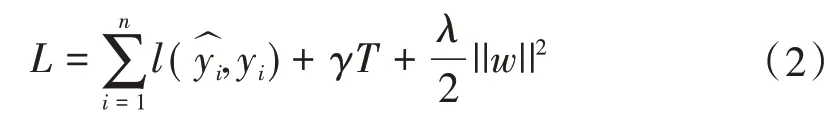
式中:l为衡量实际飞灰含碳量yi与预测的飞灰含碳量之间的差值;为损失函数的惩罚项,它通过对模型的复杂度进行惩罚来提高模型的泛化能力,ω为每棵树上叶子的权值,T为决策树的叶子数量,λ与γ为系数。
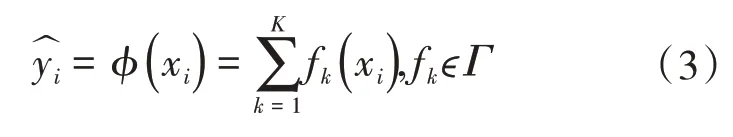
式中:k为决策树的数量;Γ为决策树的集合;fk(xi)为样本xi在第k棵树上的预测结果。
在训练的过程中,树的建立过程由计算公式(4)给出。
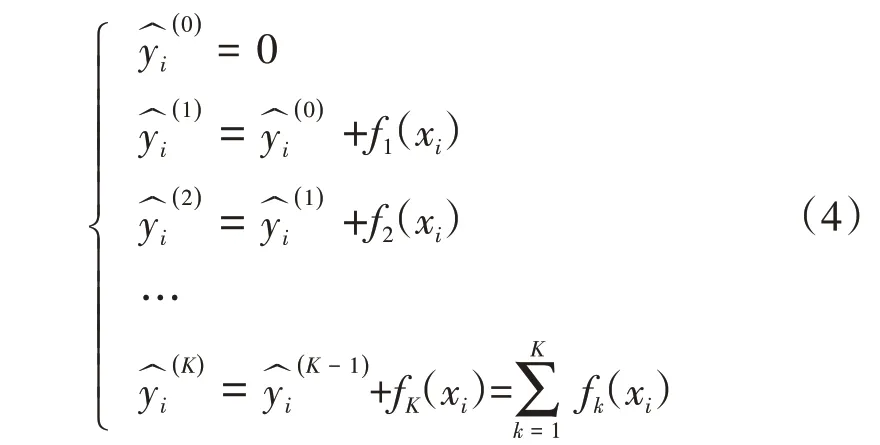
2.3 知识蒸馏架构
Hinton[15]等提出知识蒸馏的方法,用结构复杂、参数较多的Teacher 模型训练,利用其预测输出作为Student 模型的软目标;然后利用轻量的Student 模型进行二次训练,从而在分类问题中可以得到与复杂Teacher模型相近的结果。
首先,运用Teacher 模型学习出从分钟级工况和煤质数据到小时级飞灰含碳量的映射。训练完成的模型则可以得到分钟级的飞灰含碳量计算结果。为了完成不同采样周期的监督学习,对Teacher 模型的损失函数进行重新构建

式中:LTSR-T为Teacher 模型的损失函数;n为目标样本的数量,即实际得到的飞灰含碳量数量,每个目标样本之间的时间是6 h;i为第i个样本为Teacher模型的分钟级飞灰含碳量预测值;j为对应第i个时间段内的第j分钟样本,因此是分钟级的模型预测;t为第i个时间段内的分钟数,由于飞灰含碳量的实际观察时间间隔为6 h,因此t为360。
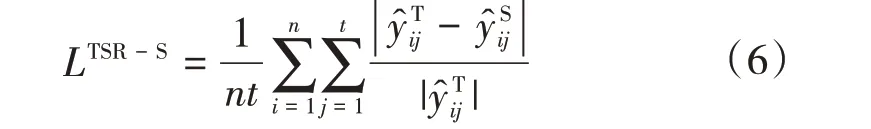
式中:为Student模型的分钟级飞灰含碳量预测值。
综上,基于知识蒸馏的飞灰含碳量预测预测流程为:
1)对分钟级锅炉运行工况参数、煤质参数和小时级的飞灰含碳量实际观测值进行数据提取和预处理;以工况和煤质数据作为输入数据,飞灰含碳量作为目标数据,形成总体训练数据集。
2)将分钟级输入数据输入到Teacher 模型中,输出分钟级飞灰含碳量预测数据,得到软目标;通过修改损失函数,完成模型训练。
3)将训练完成Teacher 模型分钟级预测结果作为Student 模型的目标值,对模型进行训练。输入数据同样为步骤2)中的分钟级输入数据。
4)将新的分钟级输入数据输入训练完成的Student模型即可得到预测分钟级飞灰含碳量数据。

图3 基于知识蒸馏框架的飞灰含碳量预测流程
3 数值试验
本次数值试验选取山东省某电厂额定容量680 MW机组2018 年全年锅炉运行、煤质及飞灰含碳量数据。其中:锅炉运行数据为分钟级采样,煤质和飞灰含碳量为每6 h采样。为了对比验证模型的效果,分别选取了单独使用Teacher 模型以及Teacher⁃Student模型2个方案。在利用2种方案进行训练时,首先对所有样本进行随机抽取处理,即打乱数据的顺序;然后对所有样本均按照7∶3 的比例划分训练集与测试集;在训练集上训练模型后,再在测试集上验证模型的效果。
预测结果显示模型在测试集上的10 次试验的平均误差。采用Teacher⁃Student 模型的测试集误差较仅用Teacher 模型下降16.5%,同时每个数据点的预测准确度还更加稳定,如表2所示。

表2 模型测试集误差 单位:%
将Teacher⁃Student 方案的预测结果绘制出来与实际飞灰含碳量进行比较,如图4所示。从图4中可以看出,经过知识蒸馏的模型能够比较精准地给出飞灰含碳量的预测结果,特别是在飞灰含碳量波动较大的区间中,模型依然能够比较好地识别出数据变化的形态与趋势。
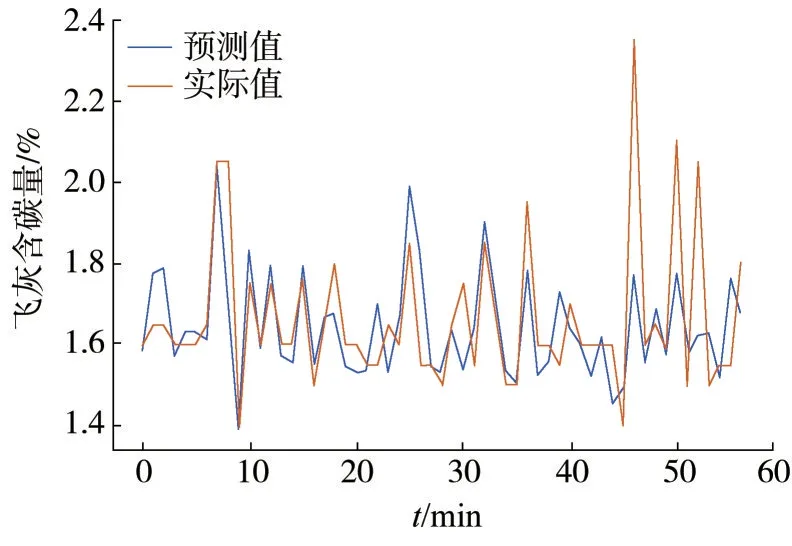
图4 Teacher⁃Student模型预测结果对比
4 结语
运用机器学习和深度学习理论和方法,在对数据运用统计方法进行预处理的基础上,构建了基于知识蒸馏架构的飞灰含碳量预测模型。通过山东省内电厂的实际试验,研究结果表明:从不同模型探索结果来看,融合Teacher和Student的模型效果优于单独的Teacher 模型,且模型的稳定性和泛化能力有了一定程度的提高。
