基于近邻传播算法的负荷不良数据辨识
2021-07-08李常刚
李 山,杨 冬,蒋 哲,周 宁,房 俏,李常刚
(1.国网山东省电力公司电力科学研究院,山东 济南 250003;2.山东大学电气工程学院,山东 济南 250061)
0 引言
状态估计是电力调度系统中的一项重要的基础功能,其通过数据采集和监测系统(Supervisory Control and Data Acquisition,SCADA)和广域量测系统(Wide Area Measurement System,WAMS)所收集到的电气量量测数据估计电网的运行状态[1]。由于电力系统规模庞大,所采集到的数据复杂多样,在数据的采集、传输、处理等各个环节中,数据均可能出现偏差或错误,造成状态估计的结果不准确。有较大偏差或错误的量测数据称为不良数据,为提高状态估计的准确度,需要对不良数据进行辨识,进一步采取相关措施对其处理。
不良数据的辨识方法主要分为两大类,传统的不良数据检测辨识方法和基于数据挖掘的不良数据检测辨识方法。传统的不良数据检测法包括有标准残差检测法、量测量突变检测法、混合检测法、量测量相关性检测法等[2];传统的不良数据辨识法主要包括有残差搜索辨识法、零残差辨识法等[3]。传统不良数据检测与辨识方法大部分是基于残差计算进行的,通常以标准残差或者加权残差作为特征值,通过概率论的假设检验,对量测结果进行逻辑判断,进而对不良数据进行辨识。传统以残差为基础的方法容易出现残差污染和残差淹没现象,造成漏检或误检,降低了不良数据的辨识准确度。许多学者为了克服传统辨识方法的缺点,采取了多种手段或方法对传统基于残差的辨识方法进行了改进,如估计辨识法、量测系统误差方差估计辨识法[4]、假设检验辨识法、基于新息差向量辨识不良数据的方法、基于模糊动态的不良数据辨识法等[5]。这些方法在计算速度、检测与辨识精度等方面取得了较大进步,一定程度上避免了残差污染和残差淹没现象。
机器学习与数据挖掘技术的进步,为不良数据检测辨识提供了新的研究思路和方法。近年来,部分学者提出了一些基于数据挖掘的不良数据辨识方法,如基于间隙统计算法(Gap Statistic Algorithm,GSA)的不良数据辨识方法[6]、基于核学习的不良数据检测与辨识方法[7]、基于模糊聚类算法的不良数据辨识方法[8]等。基于数据挖掘的不良数据辨识方法能够避免残差污染和残差淹没现象,准确度较高,计算速度快,是学者们研究的重点方向。
为提高状态估计的准确度,提出了一种基于近邻传播(Affinity Propagation,AP)算法的负荷不良数据辨识方法,并以某地区实际负荷采样数据为算例,验证了所提不良数据辨识方法的有效性。
1 AP算法
1.1 AP算法介绍
AP 算法[9]基于数据点间的“信息传递”进行聚类。将全部样本看作网络的节点,然后通过网络中各条边的消息传递计算出各样本的聚类中心。聚类过程中,共有两种消息在各节点间传递,分别是吸引度消息和归属度消息。AP 算法通过迭代过程不断更新每一个点的吸引度和归属度值,直到产生m个高质量的聚类中心。在得到聚类中心后,将其余的数据点按距离分配到相应的聚类中。与K⁃means 聚类算法或k 中心点算法等其他有监督聚类算法不同,AP 算法是一种半监督聚类算法,在运行算法之前不需要指定聚类中心个数。AP 算法寻找的聚类中心点是数据集合中实际存在的点,作为每类的代表。
假设数据样本集为{x1,x2,…,xn},为刻画数据样本之间的相似度,采用欧氏距离定义相似度矩阵S的元素为
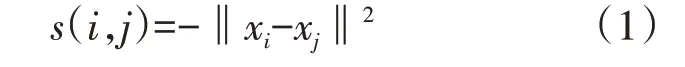
显然,当且仅当xi与xj的相似性程度大于xi与xk的相似性时,s(i,j)>s(i,k)。
AP 算法进行交替两个消息传递的步骤,以更新两个矩阵。
吸引度矩阵R的更新公式为
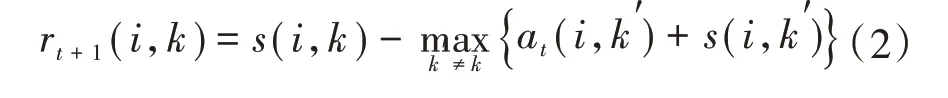
式中:t为迭代次数;s(i,k)为数据对象k和i之间的相似度;at(i,k′)为对象i与对象k′之间的归属度,rt+1(i,k)为吸引度,描述了对象k适合作为对象i的聚类中心的程度,表示的是从i到k的消息。
归属度矩阵A的更新公式为:
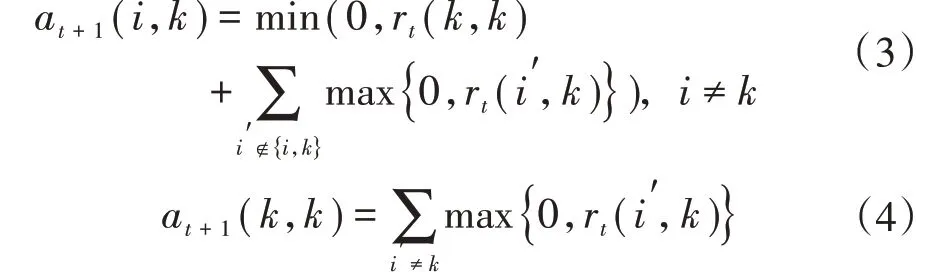
式中:a(i,k)为归属度,描述了数据对象i选择数据对象k作为其聚类中心的适合程度,表示从k到i的消息。
为防止数据出现振荡,AP 算法在更新两个矩阵时引入了衰减系数λ,λ是一个取值在0 到1 之间的实数。在加入衰减系数后,吸引度和归属度矩阵的第t+1次的迭代值为:
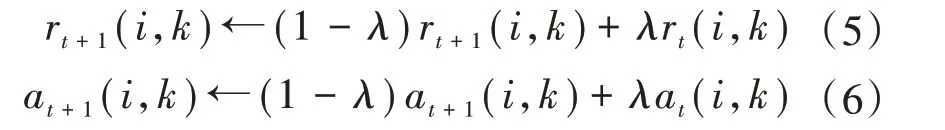
与K⁃means 聚类算法或k 中心点算法等其他有监督聚类算法相比,AP算法的优点为:
1)无须人为指定初始代表点集合。AP 算法在初始化时,将所有数据对象都作为候选的聚类中心。因此,无须人为指定初始代表点集合。在提高聚类性能的同时,也方便了人们的使用。
2)无须将数据对象表示成特征向量的形式,只需获取数据对象之间的相似度,即可对数据对象进行聚类,拓展了聚类方法的应用范围。
3)聚类中心个数的选择更加合理,且无需人为指定。在处理无法确定中心数目的情况时,能够更加灵活方便。
1.2 算法步骤
AP算法的迭代步骤如图1所示,具体为:
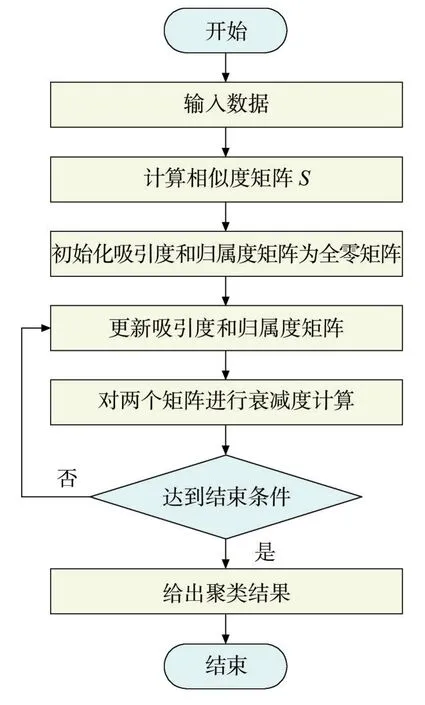
图1 AP算法迭代步骤
1)计算相似度矩阵,初始化吸引度和归属度矩阵为全零矩阵;
2)根据式(2)更新吸引度矩阵;
3)根据式(3)和式(4)更新归属度矩阵;
4)根据式(5)和式(6)对两个矩阵进行衰减计算;
5)按照步骤2)、3)、4)进行迭代,直到达到结束条件,退出计算。
迭代的结束条件为:决策经过若干次迭代之后保持不变;算法执行超过设定的迭代次数;某一小区域内的关于样本点的决策经过数次迭代后保持不变。当满足其中一个条件时,迭代结束。
2 基于AP算法的负荷不良数据辨识
对历史负荷数据和实时负荷数据的分析有助于供电部门掌握负荷使用情况,在负荷预测、用户行为分析等方面具有重要作用[10],因此需要保证负荷数据的准确性。电力负荷曲线具有相似性和平滑性两个重要特征[11],这两个特征通常也分别称为横向相似性和纵向相似性。对一个负荷区域来说,不同日期负荷曲线的波峰和波谷大体在同一个时间段,相邻几天内同一个时间段内的负荷量也相差不大,曲线的形状也非常相似,这就是横向相似性。平滑性即纵向相似性是指在同一天内,相邻采样时间点内的负荷过度会比较平滑,负荷不会有较大的突变。不良数据的存在会明显破坏了日负荷曲线的相似性和平滑性特征,据此我们可以检测出不良数据。
不良数据的辨识本质上是一个分类问题,对不良数据的辨识实际上就是对含有不良数据的日负荷曲线的辨识,将不良数据和正常数据合理分类。不良数据辨识的实质就是将含有不良数据的不正常曲线模式同正常的曲线模式分开。根据横向相似性和纵向相似性,首先定义两个指标:

式中:L(i,j)为第i天第j个时刻的负荷量;Ni为总天数;Nj为一天中的时刻数;X1(i,j)和X2(i,j)分别为横向相似性和纵向相似性,不良数据的出现会使这两个指标发生突变。为了消除不良数据对邻近数据的影响,根据这两个指标定义了两个特征值,作为分类依据。两个特征值为:
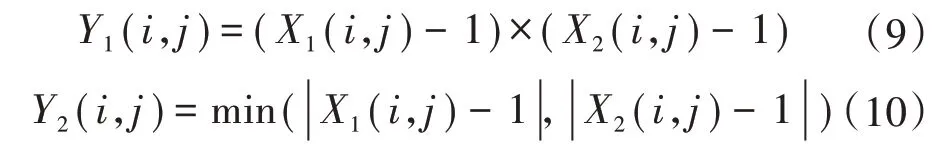
式中:Y1(i,j)被称为乘积特征值;Y2(i,j)为最小特征值。利用AP 算法,便可以按照这两个特征进行聚类分析,辨识不良数据,并且可以准确找出不良数据出现的位置。
3 算例分析
为验证所提不良数据辨识方法的准确性和实用性,以某地区供电部门的10 天共960 个采样点的实测负荷数据为研究对象进行算例分析。表1 给出了该地区1 天当中00:00—24:00 共96 个采样点的详细负荷数据,负荷曲线如图2所示。

图2 某地区日负荷曲线

表1 某地区1天内96点负荷数据
原始的负荷数据不包含不良数据,为了验证所提方法的有效性,对原始数据进行了改造。AP 算法中的衰减系数设为0.5,最大迭代次数设为100 次。在负荷数据中加入一个不良数据,进行不良数据辨识。首先求取负荷的乘积特征和最小特征,对其进行聚类,聚类结果如图3 所示。图3 中,聚类1 表示的是不良数据,聚类2 是正常数据,通过该聚类方法,可以准确地辨识出不良数据,不良数据和正常数据具有明显区别。
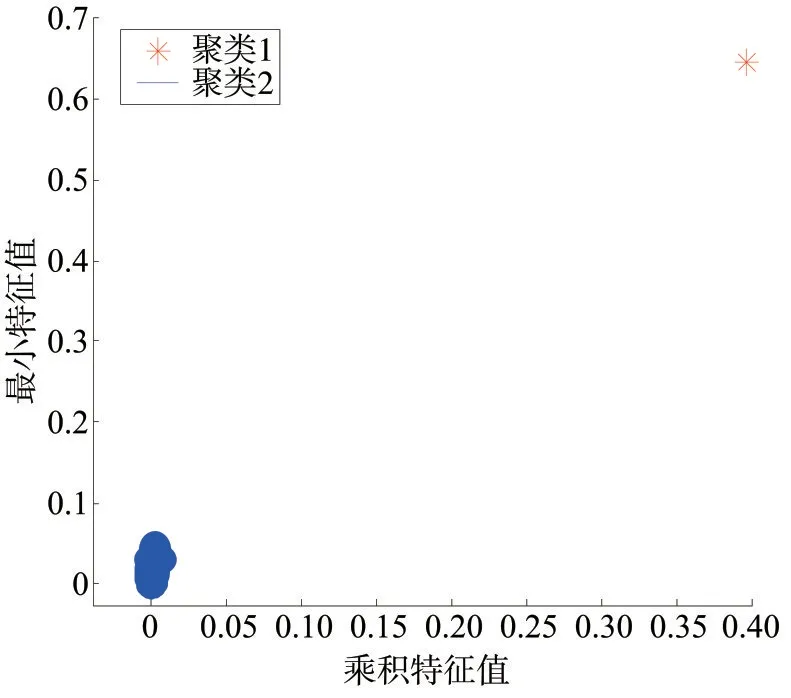
图3 单一不良数据下AP算法聚类结果
在原始数据中加入3 个不良数据,进行多不良数据辨识,并与K⁃means 聚类进行比较,由于在辨识之前无法知道聚类个数,在使用K⁃means 聚类算法时将聚类中心数目设为2,希望能将数据分为不良数据和正常数据两类。图4 为本文所提方法的聚类结果,图5 为K⁃means 聚类的聚类结果,本文所提方法将数据分为了3 类,能够准确识别出不良数据,而K⁃means聚类只识别出一个不良数据,误将另外两个不良数据纳入到了正常数据中,发生了误判。因此,本文所提方法在不确定不良数据聚类个数的情况下,具有更高的识别度。

图4 多不良数据下AP算法聚类结果
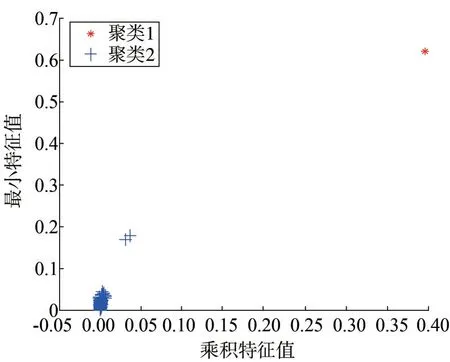
图5 多不良数据下K-means算法聚类结果
4 结语
提出了一种基于AP 算法的负荷不良数据辨识方法。与传统半监督聚类方法相比,AP 算法具有准确度高、无须指定聚类中心数目等优点,适合进行不良数据辨识。基于负荷相似性和平滑性两个特征,定义了乘积特征值和最小特征值作为分类依据,可以提高分类准确度。某地区的实际负荷采样数据算例表明,本文所提方法在单一不良数据、多不良数据情况下,均具有较高的辨识度,弥补了传统半监督聚类方法的不足。此外,所采用的AP 算法也可以推广到其他类型的不良数据辨识上,这是下一步的研究方向。
