基于有序树拓扑的配电网转供能力分析及网络重构方法
2021-07-08李方舟周博曦
李方舟,霍 健,周博曦
(1.国网山东省电力公司济南供电公司,山东 济南 250012;2.国家电网有限公司技术学院分公司,山东 济南 250002)
0 引言
目前配电网广泛采用多分段、多联络结构以及闭环接线、开环运行的方式,以实现分区段的方式调整与自愈[1-2]。随着规模的不断扩大与负荷的不断增长,配电网联络日益增多,结构日益复杂,在增加负荷转供路径,提高运行可靠性和灵活性的同时,也增加了配电网运行分析的复杂性[3]。文献[4-5]在配电网供电能力相关研究[6-9]基础上,提出配电网安全运行域(Boundary Supply Capability,BSC)的概念,针对配电网联络线路,研究了其满足N-1 条件下的最大供电负荷。但在实际运行中,配电网用户的用电负荷具有很强随机性和自发性,目前还难以通过电网调度或负荷控制将联络线路的负荷精准控制在BSC 以下。因此,根据配电网实时运行负荷状况,分析配电网分区段转供能力,对配电网调控运行及风险预控有重要的意义。
在配电网网络优化重构方面,文献[10-11]分别以提升最大供电能力、供电可靠性为目标,建立了配电网重构模型;文献[12-13]利用拓扑检测等方法,提出配电网重构的优化方法及实现方案。但以上研究均未考虑配电网的多分段多联络拓扑结构,无法实现细化至分支线层级的评估与优化。针对配电网多分段多联络结构与灵活的运行方式,文献[14]以有序树表示配电网分段分支结构;文献[15-16]基于公共信息模型(Common Information Model,CIM),分别通过追踪拓扑方法及基于开关状态的动态拓扑方法,实现配电网分段开关、分支线路的拓扑分析,为配电网分支线层面的转供能力及网络重构研究提供了新的思路。
结合配电网运行与调度的实际需求,首先针对配电网多分段多联络结构,建立配电网的有序树模型,然后基于配电网有序树模型,结合动态拓扑分析,提出配电网分区段转供能力的分析方法,在联络线路的备用裕度不满足N-1 条件下,精准分析可转供的负荷,最后以联络线路负载均衡为目标,建立了配电网网络重构优化的线性规划模型,优化后能够有效避免配电线路的重过载,提高设备利用率。
1 基于有序树的配电网拓扑模型
配电网以配电线路(馈线)为基本单元,为直观表示其分段联络结构,可以“节点—线段”的连接方式,反映“开关—支路”连接关系,并表示为若干个以电源为根的树[13],分支线设备对应的有序树模型如图1所示。
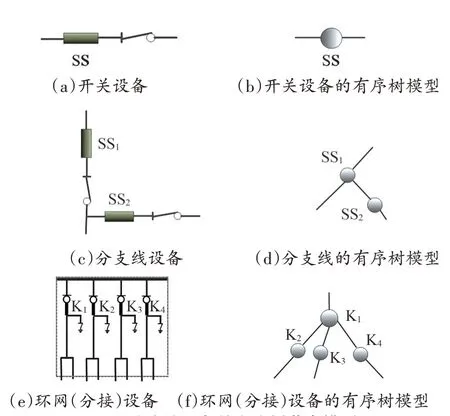
图1 分支线设备的有序树节点模型
以线路的变电站内出口开关为根节点,以下每级分段开关为子节点。对于联络线路,以出口开关至联络开关经过的连接路径为主路径,其他分支线为分支路径,从而更方便地开展配电网通过线路间联络实现转供、负荷分配及优化重构方面的分析。如图2 所示为3 条联络线路组成的配电系统有序树模型,图2中,B1、B2、B3分别表示3条馈线的出口电源端,SS 表示分段开关,SL 表示联络开关,K 表示环网设备开关,在线路拓扑分析中,可等价为分段开关。显然,在如图2 所示配电网接线组中,B1经分段开关SS1、K1、K2、SS2、联络开关SL1至B2以及B1经分段开关SS1、K1、K4、SS3、SL2、SS4至B3为两条联络主路径,其他分段开关所在路径为分支路径。

图2 配电网有序树拓扑模型
在图2 所示的配电网联络线路模型中,无论运行方式如何变化,SS5、SS6所示的线路末端分段开关,以及K3所示的分支路径上的分段开关,其功率流向均是固定的,为开关流向末端,因此这些开关均为单向开关,在有序树拓扑中对应的为单相节点,而SS1、SS2、SS3、K1所示的分段开关,以及SL1、SL2所示的联络开关,其功率方向可能有两种,为双向开关。更进一步,图2 中K1节点为B1—B2及B1—B3两个主路径的交汇节点,除上层节点SS1外,下层也有K2、K4两个节点可作为电源,这样的节点,可表示为双向分支节点。表1 列出了图2 中配电网有序树模型中节点的分类及其对应的开关设备。
由表1 可知,分支路径上所有节点均为单向节点,而主路径上所有节点均为双向节点。多联络的环网箱、分支线对应为双向分支节点。
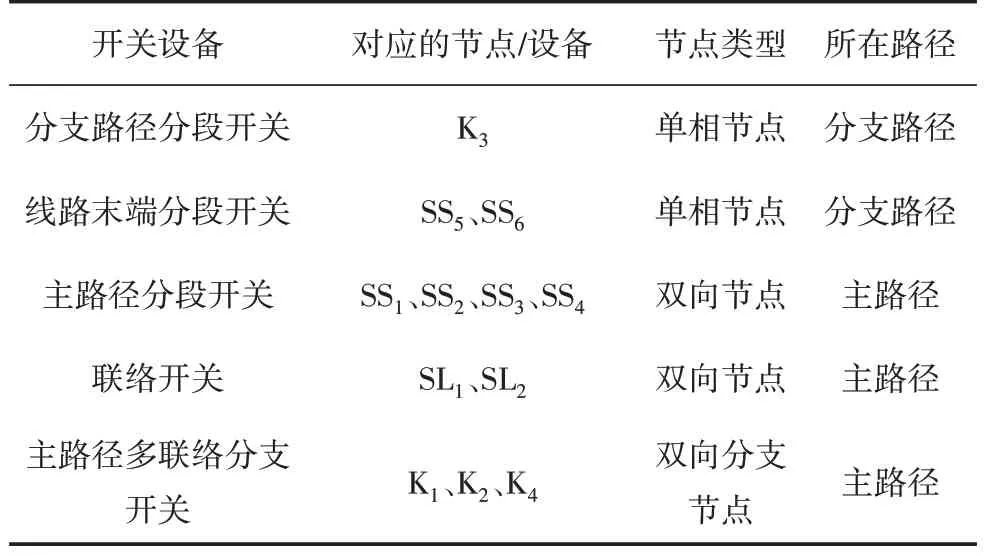
表1 配电网有序树模型节点分类及其对应的开关设备
基于IEC 61968 中用于配电网建模的CIM 扩展模型,对于支线开关Sk(包括分段开关SS及联络开关SL),若Sk为分段开关或分支开关,则存在其下一级节点Sk+1,两开关间线路区段表示为[Sk,Sk+1]。显然,线路区段[Sk,Sk+1]为开关Sk供带的最小的线路区段,也是分析配电网分区段转供能力及优化重构的最小单元,记为BranchSk=[Sk,Sk+1]。
2 基于有序树模型的配电网转供能力分析
通过线路间联络实现负荷的快速灵活转供是配电网安全高效运行的一项基础条件,分区段分析配电网转供能力,即根据配电网实时运行负荷状况,确定在N-1情况下配电网的可转供区间及不可转供区间。在实际运行中,考虑到线路长度及电压调节和无功补偿装置,电压约束对中压配电网相对宽松,因此,对中压配电网的相关分析普遍采用直流潮流模型。相关研究表明,直流潮流的模型在中压配电网供电能力分析中是适用的[1],对中压配电线路馈线出口故障最严重,因此在配电网转供能力分析中,主要考虑馈线出口故障[1-5]。
对于线路i,若其负荷为Li,额定容量为,则其负荷裕度Mi为

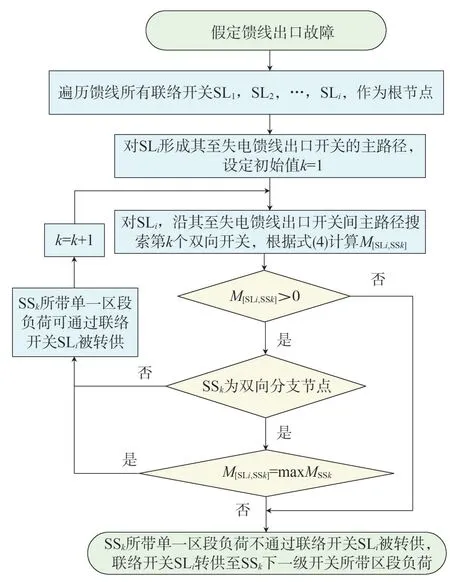
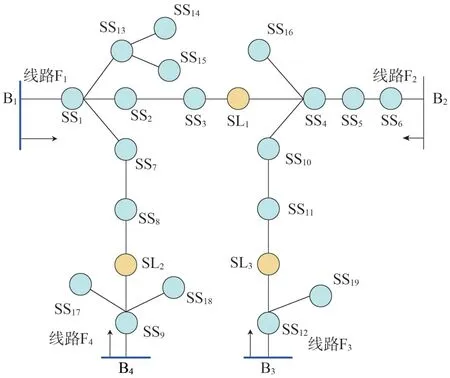
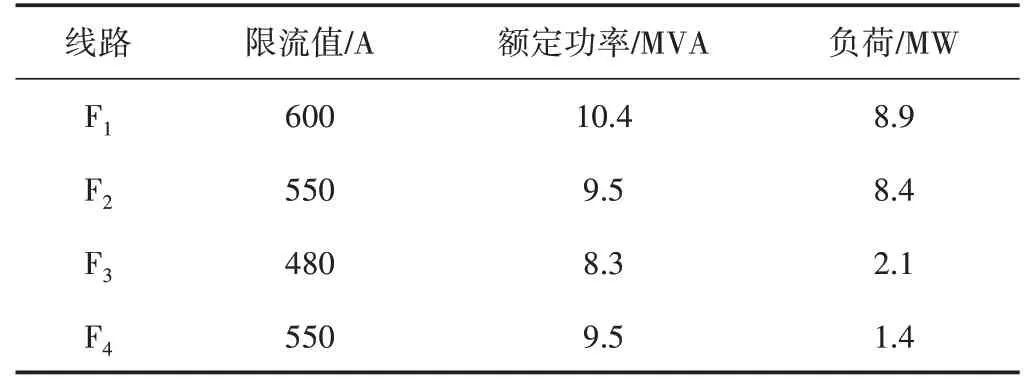
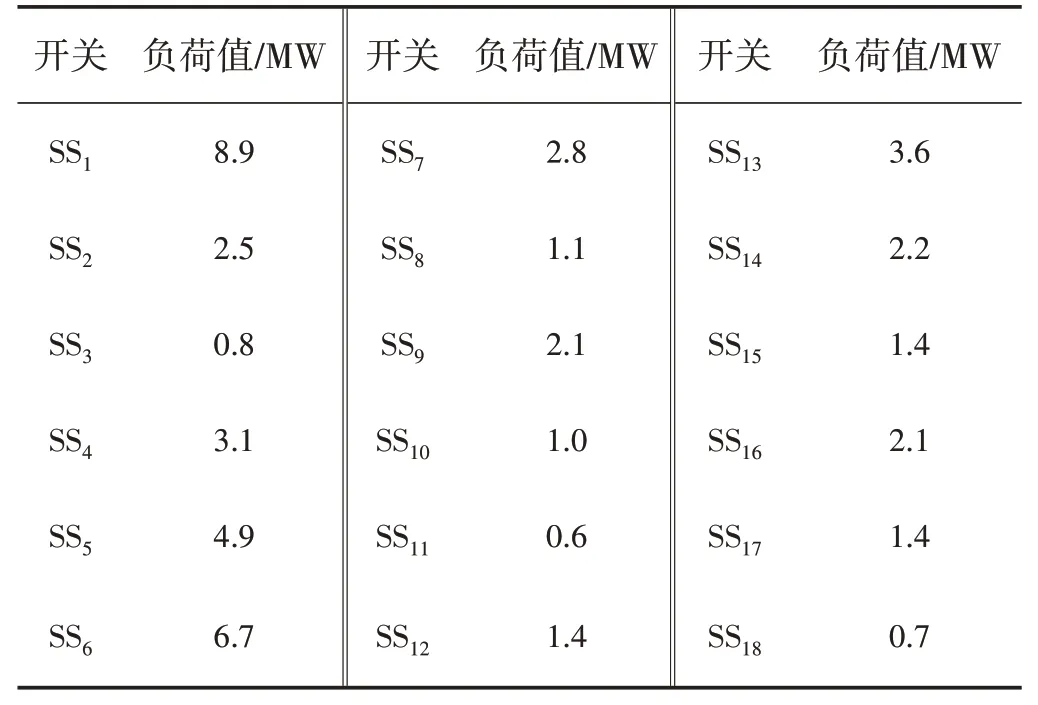
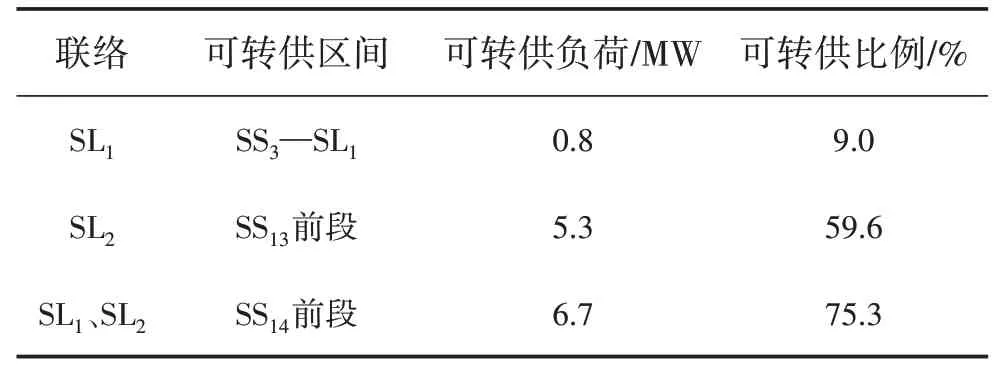
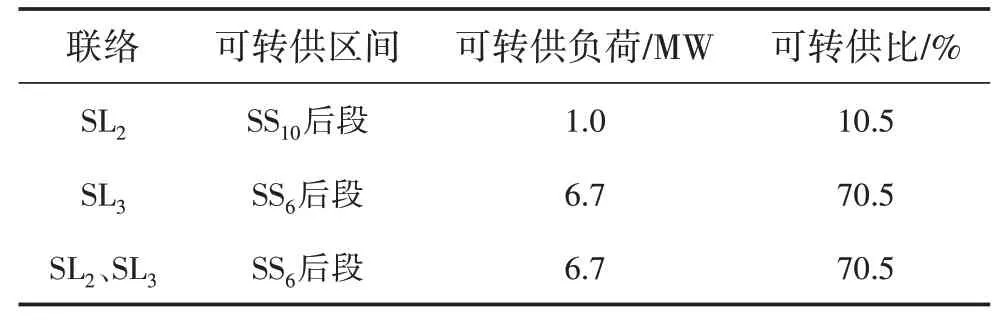
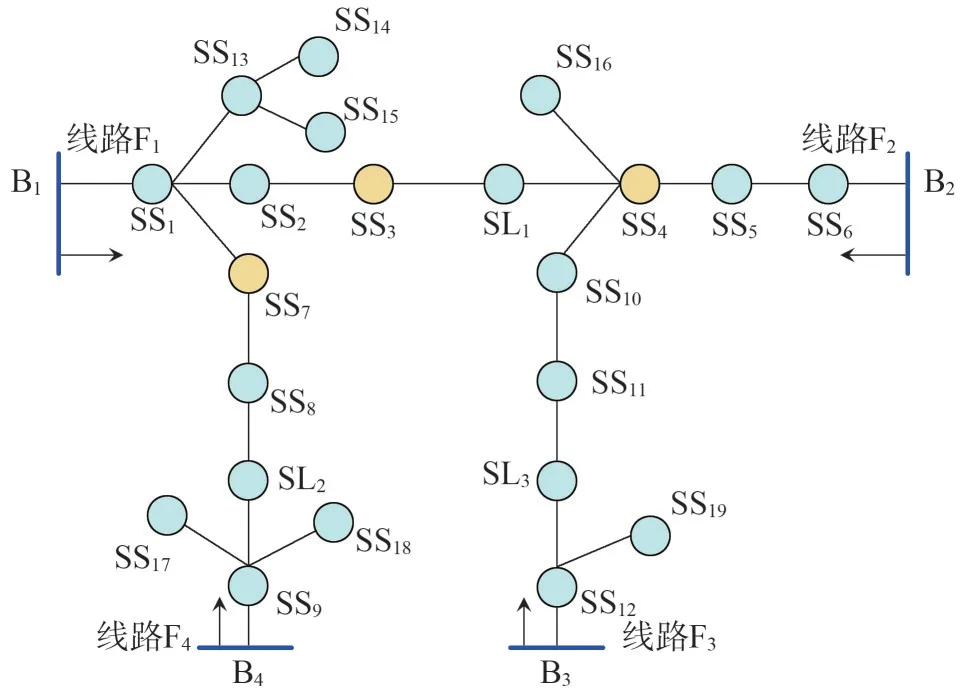
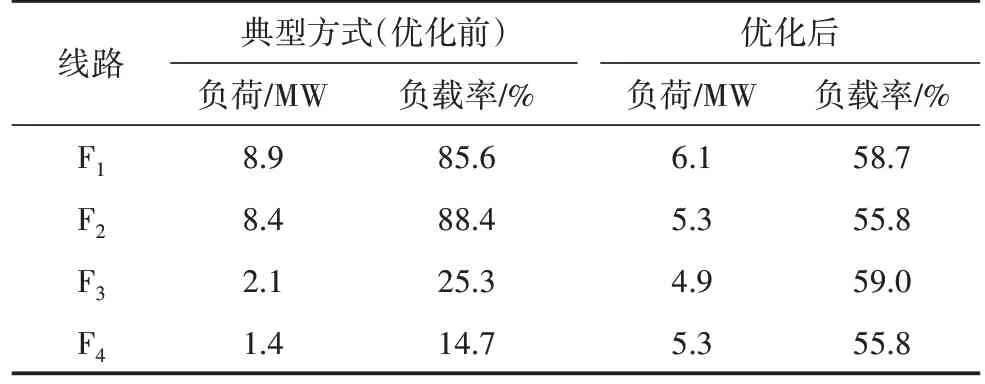
对于联络线路i及j,若Mi>Lj,在线路j发生馈线出口故障失电情况下,其全部负荷均可由线路i转供;若Mi 若线路j为如图3所示的单联络线路,仅有线路i作为备用,对于线路j主路径上的分段开关SS1,SS2,…,SSm,可根据式(2)确定开关SSk后段区间为可转供区间,SSk前段区间为无法转供区间。 图3 单联络线路有序树拓扑示意 式中:LSSk与LSS(k+1)分别为流过SSk及其上一级分段开关SSk+1的负荷。 若线路j为多联络线路,通过联络线路分区段转供时,须结合联络线路的负荷裕度与拓扑结构分区段确定最优转供方案,以最大化利用联络线路的备用容量。 通过配电自动化终端读取每个开关设备的实时负荷,可以计算每个区段的负荷值。对于支线开关SSk,若为末端负荷开关,则其后段负荷值Lk=LSSk,若SSk为分段开关或联络开关,则其供带下级最小区段BranchSSk的负荷为 线路负荷分区段通过联络开关SLi转供,转供至开关SSk下级区段BranchSSk后,对侧联络线路的负荷裕度M[SLi,SSk]为 式中:M为联络线路的负荷裕度。 对多联络线路进行分区段转供能力分析,假设其通过n个联络开关SL1,SL2,…,SLn与其他线路联络,则可形成SL1,SL2,…,SLn至该线路站内开关的n条主路径,自各联络开关开始,通过式(4)逐级计算开关BranchSSk能否由其所在主路径上联络开关转供。 对于图2 中K1、K2、K4所示的主路径多联络分支开关,若多个联络线路的负荷裕度均能够带其所带最小区段的负荷,则其中负荷裕度最大的一组,具备继续供带更多区段负荷的可能性,因此,若节点SSk为多联络分支节点,则须确定供带BranchSSk后负荷裕度最大的一个联络路径,记为max: 遍历所有联络开关SL1,SL2,…,SLn,利用有序树拓扑模型沿各自主路径逐级向上进行拓扑搜索,并通过式(4)与式(5)计算负荷裕度,最终确定每个联络开关所能转带线路区段的集合,即为该线路的可转供区间。多联络线路转供区间分析流程如图4 所示。 图4 多联络线路可转供区间分析流程 一般情况下,配电线路由变电站内出口开关供带本线路负荷,线路间联络开关热备用。在实际运行中,由于线路负荷增长的随机性及线路改造的滞后性,存在大量负荷分配不均衡的情况,在负荷高峰期,某些线路易出现重载甚至过载。因此,以各配电线路负载均衡为目标,通过联络开关及分段开关,实现联络线路的分区段优化重构。一方面有效避免线路过负荷,提高配电网运行在正常状态时的容量裕度,减轻调度及运行人员的工负担,另一方面可以通过优化运行方式,减少线路改造工程量,节约投资成本。 借鉴配电网供电能力模型中主变压器负载均衡度的定义[6],将配电线路负载率的方差定义为联络线路的负载均衡度VVLR作为优化的目标,即 式中:N为参与优化的联络线路的数量;RFi为线路i负载率,等于线路实际负荷与额定负荷的比值,即 对于中压配电网,由于电压约束较为宽松,因此约束条件一方面为各线路及其所在主变压器负荷不超过其而定容量限值,另一方面,须考虑配电线路通过联络开关转供多级分支线后,线路长度不超过变电站内开关的保护范围。因此,优化模型的约束条件为 式中:Tpmax和Tpmin分别为主变压器p的最大、最小负载限额;Xi为第i条线路本身的阻抗;x(i)、l(i)分别为第i条线路通过联络开关供带的最长路径中,各区段线路的长度及相应导线单位长度的阻抗值,Xi+∑x(i)l(i)即为重构后第i条线路最末端的阻抗值;为根据线路i的限时电流速断保护整定值,在系统最小运行方式下归算得到的最大阻抗值。 由式(6)、式(8)表示的优化模型中,约束条件均为线性函数,因此式(6)、式(8)表示的优化模型为线性规划模型。以每个分段开关供带的最小线路区段及其负荷为分计算单元,通过线性规划方法求解,可求得线路负载均衡重构后的最优运行方式。 以某供电区4 联络线路配电系统为例,说明基于有序树拓扑的配电网转供能力分析及网络重构方法。简化后的网络拓扑如图5 所示。在正常运行方式下,4 线路均由站内开关作为电源,线路各分段开关SS1—SS19在运行状态,联络开关SL1、SL2、SL3在热备用状态。表2列出了4条线路的限流值、额定容量及某典型运行方式下的负荷数,表3 列出了该运行方式下流过各分段开关的负荷。 图5 某供电区4联络线路接线组简化拓扑 对负荷较重的线路F1、F2进行转供能力分析。由表2 及表3 可知,在典型运行方式下,线路F1、F2均不具备N-1情况下将负荷完全转供的能力。对线路F1,首先分别考虑仅有SL1及SL2单个联络情况,分析其可转供区间及可转供负荷量,然后同时考虑SL1及SL2两个联络点,通过图3 所示方法分析其可转供区间及可转供负荷量,结果对比如表4 所示,同样的方法对线路F2进行分析,结果对比如表5所示。 表2 线路限流值、额定容量及负荷 表3 各分段开关负荷值 表4 典型方式下线路F1可转供区间及负荷量 表5 考虑全部联络情况下线路F1、F2可转供区间 在表4 中,单独考虑联络SL1,线路F1在出口开关故障情况下可由线路F2供带分段开关SS3后段0.8 MW 负荷;而单独考虑联络SL2,线路F1在出口开关故障情况下可由线路F3供带分段开关SS13前段5.3 MW 负荷;若考虑F1负荷由线路F2、F3分别转供,则可由线路F2通过SL1转带SS3后段,由线路F3通过SL2转带站内出口开关至分段开关SS3及SS14间线路所带负荷,总共6.7 MW负荷可以转供。而在表5中,由于联络点SL1及SL3均由SS4、SS10及SS16构成的末端环网设备配出,因此考虑SL2、SL3两个联络与考虑SL3单个联络时可转供容量相同,均为6.7 MW,多个联络并未增加有效备用容量。 对图5 所示的4 联络线路系统,在表2 及表3 所示典型运行方式下,根据式(6)及式(8)构建优化模型。在配电线路三段式电流保护定值的整定中,已经考虑线路供带联络线路,因此在本算例中,联络线路串带长度不超过对侧线路全长情况下,忽略保护定值对线路长度的约束。利用线性规划方法求得优化重构结果如表6、图6 所示。表6 中,开关位置“1”表示开关在合位,“0”表示开关在分位。 图6 优化后各分段开关及联络开关位置及系统简化拓扑 表6 优化后各分段开关及联络开关位置 优化前后各线路负荷值及负载率对比如表7 所示。在表7中,正常运行方式下,线路F1、F2的负载率均超过80%,已达到重载的限额,随着负荷的增长,极易发生过负荷,需要调控人员采取调整运行方式、压降负荷等措施。通过优化重构,各线路负载率均在55%~60%之间,不仅避免了线路过负荷的风险,减少了调控及运行人员对过负荷异常处置的工作量,还有效提高了设备利用率。 表7 优化前后各线路负荷值及负载率对比 目前配电网广泛采用多分段、多联络结构以及闭环接线、开环运行的运行方式,结合配电网结构及运行方式,分区段研究配电网的转供能力及网络优化重构,具有重要的理论意义和实用价值。结合配电网运行的实际需求,提出一种配电网转供能力分析及网络重构方法。将配电网分段联络结构简化为有序树模型;通过对有序树模型开展动态拓扑分析,分区段计算N-1 情况下的可恢复区间;以联络线路负载均衡为目标,建立网络重构优化的线性规划模型,实现多联络配电网的优化重构。实际案例的分析结果证明了该方法可以在精准的分析N-1情况下的恢复能力,均衡配电网负载,提高配电网运行效率。 目前只针对配电网典型运行方式进行了转供能力分析及网络重构优化,下一步可结合智能优化算法,针对规模较大、运行方式复杂的配网开展转供能力分析及网络重构优化方法展开研究,以提高本文所提方法计算效率和的适用范围。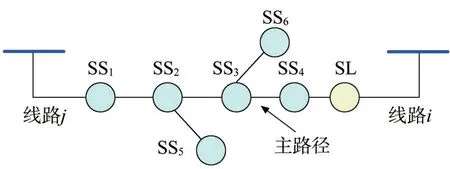


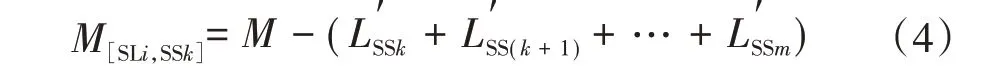
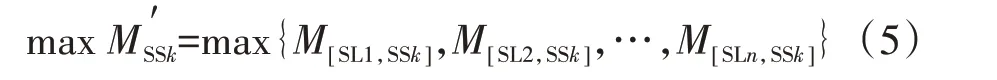
3 分区段优化重构方法
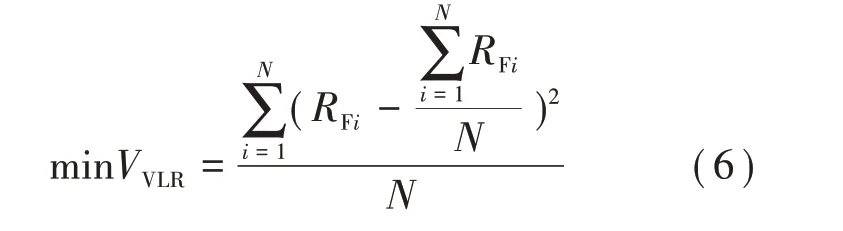
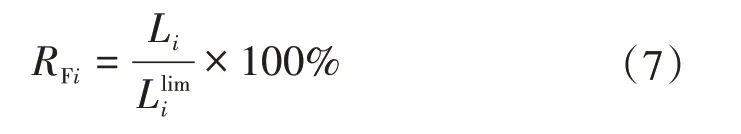
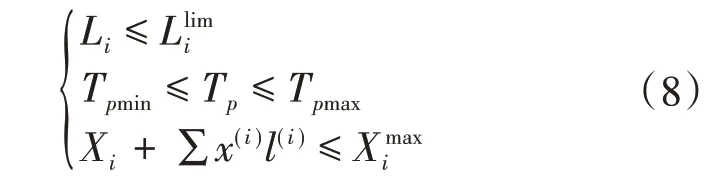
4 实例分析
4.1 转供能力分析结果
4.2 网络优化重构结果

5 结语
