丰盈过程 放飞思维

江苏省常州市新北区九里小学 陈 莉

苏教版数学教材，在每一单元的后面都设置了相对应的练习，这些练习不仅能帮助学生有针对性地巩固新知，还能拓宽学生思考问题的方式。但是，习题的呈现方式都比较简单，如果不深入发掘，有效设计，学生对习题的理解只能是流于表面，不能让经典的习题产生价值最大化。例如，苏教版数学五年级下册《解决问题的策略》一课的习题为例（如图1）。

图1

无独有偶，这道习题和人教版数学六年级上册第八单元的数学广角“数与形”（如图2）有惊人的相似。如果这道题仅仅是停留在掌握这一组习题的规律，那么隐藏在形式后面的内涵价值就完全被忽略了。如何有效地利用好这一习题？笔者做了如下设计：

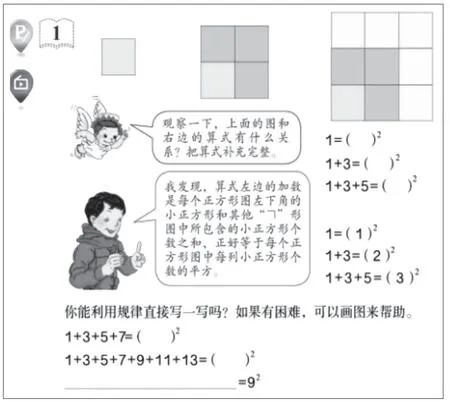
图2

一、设置问题，引领思维的方向

问题是思维的核心。数学活动的开展是有一定的目标的，而目标直接体现于课堂的方式便是问题，因此，设计有指向性的问题能准确引领学生思维的方向。教学时，我们可以先出示一道算式：1+3+5+7+9+11+…+100=？面对这样一道复杂的习题，学生一开始可能手足无措，但是教师要引导学生去观察这道题的规律，确定从最简单的1,1+3,1+3+5,1+3+5+7开始研究，然后通过“算一算，比一比，你有什么发现”等大问题的引领，帮助学生确定研究的路径。

二、提供素材，激发思维的碰撞

《义务教育数学课程标准（2011年版）》在“课程资源开发与利用建议”中指出：教师应充分利用日常生活中与数学有关的信息，开发成教学资源……促进不同的学生在数学上得到不同的发展。素材的提供，能引发学生研究的兴趣，触发学生探究的灵感，激发学生思维碰撞的火花。在学生做完1，1+3，1+3+5，1+3+5+7等算式后，教师相机出示书上的内容（第7大题中的第1小题），组织学生继续填一填，想一想，算式与相对应的图形之间有什么联系？接着可以让学生模仿着任意写几个算式，并提供方格纸(如图3），让学生在方格纸上继续画一画，然后引导学生有序地观察比较加数有什么特点，和图形有什么联系？和有什么特点？与图形之间又有什么联系？学生通过观察思考发现：加数对应的是L形所包含的圆形个数；和可以写成大正方形每行或每列个数的平方。图形与方格纸这两种素材的提供，激发了学生思维的碰撞。

图3

三、撰写报告，呈现思维的轨迹

不管是哪一种数学学习方式，都伴随着数学思维的动态进程，而思维的内容仅凭大脑的记忆是有限的。如果能撰写报告，呈现出思维轨迹，那么学生的思考过程会找到一个可靠的支撑点。因此，给学生提供这样一份实验报告不失为一种上策。

等式左边 奇数个数 和 等式右边 图形（1）1（2）1+3（3）（4）（5）我的发现：

这份报告，整理了观察探索的过程，呈现了思考的痕迹，让我们的探究过程有理、有据、有序。

四、追本溯源，提升思维的深度

学生通过上面一系列的研究，发现：算式左边的加数是大正方形右上角的小圆和其他“L”形图形所包含的圆形个数之和，它们的和正好等于每行或每列小正方形个数的平方；或者说“从自然数1开始的连续奇数的和”还有一个特殊的名称叫“正方形数”。如果仅仅记住这个结论，那么学生对规律的探索也就仅仅停留于表面。学生只有真正搞清楚规律内在的原理，才能理解规律掌握规律，从而提升思维的深度。因此，接下来笔者又设计了三个问题：（1）这个规律为什么要从自然数1开始？能不能直接从3开始？（2）为什么一定要连续奇数？去掉一个奇数行不行？（3）为什么一定是奇数相加？添上一个偶数行不行？连续三个问题，促使学生不得不去思考规律的内涵本质，结合图形，学生会发现：如果没有1，或者不连续，正方形就不完整，更谈不上正方形数；因为L形是一个轴对称图形，顶点处一个，两边对称，因此，L形所包含的小正方形个数永远是奇数。这一过程通过数形结合、相得益彰地对数学规律进行了详细的阐述，从而极大地提高了问题的趣味性、思考性和挑战性。

五、变化练习，提高思维的广度

一个规律的掌握，需要相关的习题进行巩固。习题的设计要有层次性，既要有针对基本规律的基础性练习，又要有提高思维灵活性的变式练习，习题不在于多而在于精，因此，笔者设计了四道习题：

这四道习题的设计，既有正向思维的训练，又有逆向思维的培养，每个层次的学生都会有不同的收获，正所谓“不同的学生学不同的数学”。

我们的数学课堂，只有不断发掘教材内涵，丰盈教学过程，才能放飞学生的思维，从而提高课堂品质。