地下铲运机铲装轨迹数学建模与仿真*

□ 赵晓燕 □ 郭 鑫,2 □ 姜 勇 □ 高泽宇 □ 张元清

1.矿冶科技集团有限公司 北京 100160 2.北京科技大学 机械工程学院 北京 100083

1 研究背景

地下铲运机是地下金属矿山开采中的重要运输设备,地下金属矿山的智能化开采是当今行业发展的必然趋势,地下铲运机的自动铲装是智能化开采的关键技术之一[1-2]。地下铲运机在铲装工作中,通过控制动臂油缸和转斗油缸的伸缩量来调整铲斗位姿,从而完成铲装作业。笔者选取合适的铲装方式和常见的料堆形状轮廓后,规划出理想铲装曲线。根据地下铲运机工作装置的运动学分析,完成铲斗斗刃位置与动臂油缸伸缩量和转斗油缸伸缩量的函数关系,实现铲斗斗刃的轨迹曲线数学计算。利用仿真软件模块对地下铲运机工作装置进行机构学建模,完成目标铲装轨迹曲线与仿真铲装轨迹曲线的误差分析,为后续的控制器设计提供仿真模型。

2 铲装方式

在地下铲运机自动铲装过程中,需要对铲斗轨迹进行跟踪控制。铲斗轨迹的跟踪控制是建立在铲斗轨迹规划基础上的。对地下铲运机铲斗轨迹进行规划,需要结合地下铲运机铲装过程中采取的不同铲装方式及料堆的形状轮廓,为此需要对不同的铲装方式和料堆形状轮廓进行分析。在确定铲装方式和料堆形状轮廓的基础上,对铲装轨迹进行规划处理。

经查阅文献,现有地下铲运机的铲装方式主要有三种[3]。

(1) 一次铲装法。地下铲运机向前行驶,推动铲斗铲入料堆,直至铲斗后壁和料堆接触。此时,地下铲运机停止前进,翻转铲斗或者举升铲斗完成铲装。这种铲装方式需要地下铲运机提供很高的功率来克服阻力,常用于煤炭、黄沙等松散物料的铲装。

(2) 配合铲装法。在地下铲运机向前行驶的同时,配合转斗油缸或动臂油缸的动作进行铲装作业,提升动臂并且翻转铲斗。这种铲装方式的目的是使铲斗斗刃的轨迹与料堆形状轮廓大致平行,承受较小的铲装阻力,提高铲装效率。

(3) 分段铲装法。地下铲运机采用分段铲入和举升的方法,铲斗铲入一定深度后,地下铲运机停止前进,翻转铲斗使料堆回落,然后再次铲入、翻转铲斗以保证满斗率。这种铲装方式易损坏铲斗零件,对工作装置的强度有较高要求。

针对以上三种铲装方式,由铲装对象及优缺点分析可知,采用配合铲装法,能够铲装大块料堆,减小铲装过程中受到的阻力,符合现有地下铲运机的铲装特性。为此,笔者以配合铲装法为主进行分析。

3 料堆形状轮廓

对料堆形状轮廓进行研究归纳,主要有三种,如图1所示[4-5]。

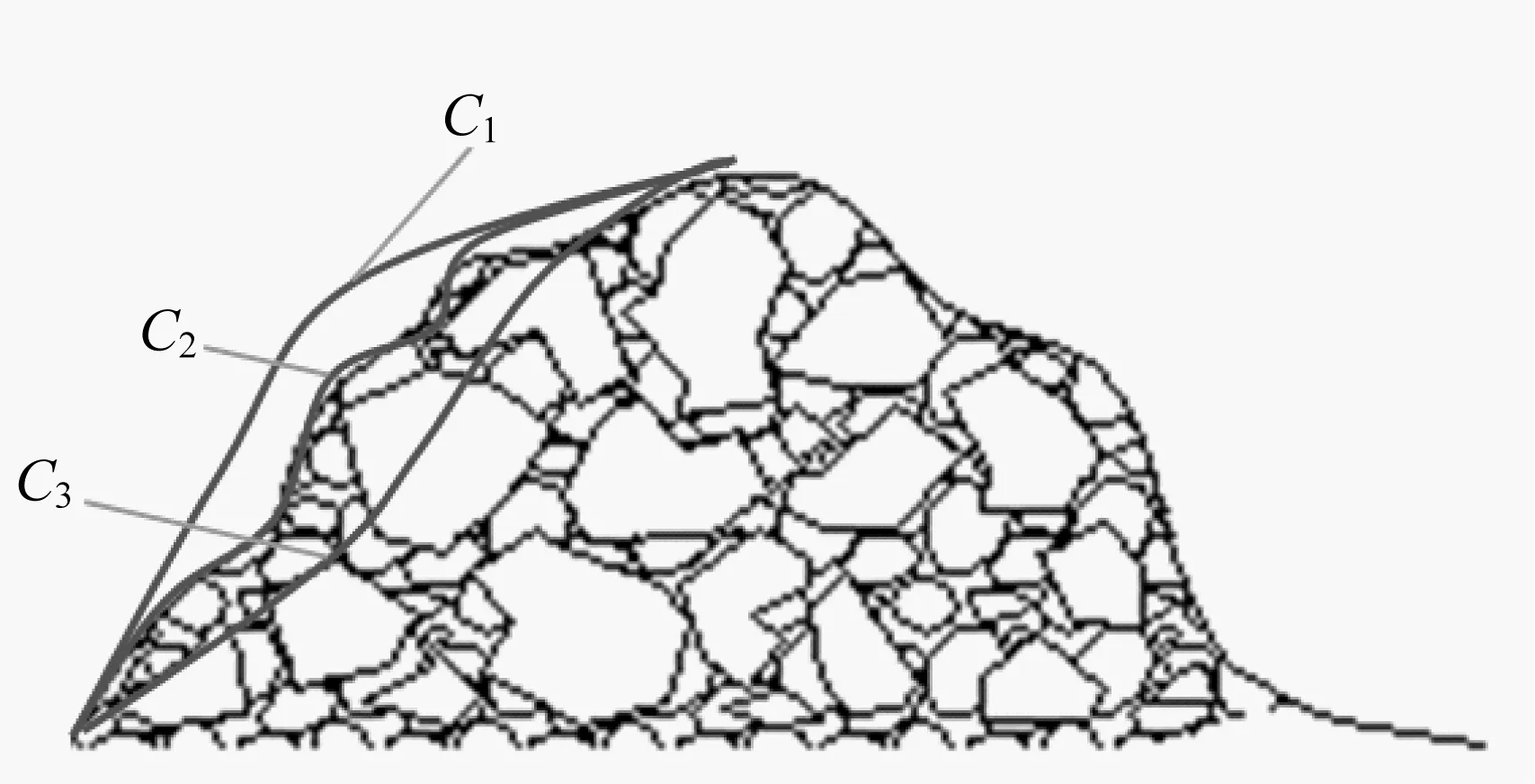
▲图1 料堆形状轮廓

料堆由于堆积方式的特殊性,造成曲线C1外凸,料堆在上层相对挤压。曲线C2是现有普遍状态下的料堆形状轮廓,坡度近似为40°～45°料堆安息角。料堆由于粒度太小造成下滑,导致曲线C3凹陷,这种情况存在但较少。为适应现有条件下的铲装方式,选取具有普遍代表性的曲线C2进行理想铲装曲线的规划分析。

4 理想铲装曲线规划

在选取合适铲装方式及普遍存在的料堆形状轮廓后,以曲线C2为例,对料堆进行理想铲装曲线规划。

(1) 确定地下铲运机铲斗斗刃坐标。建立斗刃坐标系,以斗刃与料堆的接触点为原点,地下铲运机前进方向为X轴正向,竖直方向为Y轴。

(2) 确定插入深度。根据对应的铲装曲线确定相应的插入深度。

(3) 根据地下铲运机铲斗特性,确定铲装曲线与料堆形状轮廓的包围面积S,由此设定铲装曲线为二次曲线,建立方程:

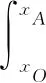
(1)

式中:xO、xA、xB依次为铲装起点水平位置、水平插入终点水平位置、铲装阶段终点水平位置;fC2、fOA、fAB依次为料堆形状轮廓曲线、水平插入曲线、铲装阶段曲线。

二次曲线在A点取极小值。

(4) 根据求解结果,生成地下铲运机铲斗斗刃的运行轨迹曲线。

结合KCY-2型地下铲运机,对理想铲装曲线进行分析。建立一个铲装轨迹计算坐标系,将地下铲运机铲斗放平,以铲斗斗刃刚碰到料堆时动臂的固定铰点为坐标原点O0,前进方向为X0轴正方向,垂直地面向上为Y0轴正方向,如图2所示。经实际测量,铲斗斗刃O2的坐标为(3.291 9 m,-1.283 1 m)。

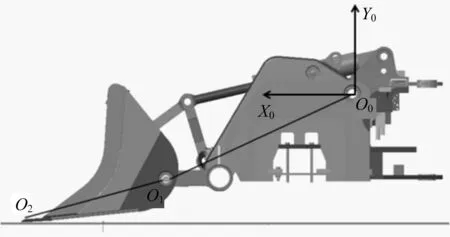
▲图2 铲装轨迹计算坐标系

为确保自动化操作的连贯性,铲装轨迹曲线应连续且光滑,由此设计铲装轨迹曲线,如图3所示。

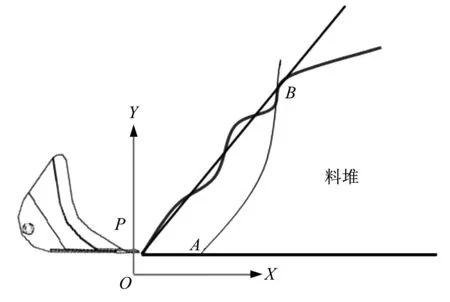
▲图3 铲装轨迹曲线

在直线OA阶段,动臂油缸和转斗油缸保持不动,铲斗接近水平,地下铲运机以速度v1匀速推动铲斗铲入料堆,插入深度一般为30%～50%铲斗斗底长度。OA长度经计算为0.306～0.510 m,为方便计算,取中间值0.4 m。

在曲线AB铲取阶段,地下铲运机以速度v2匀速推进铲斗,并开始举升动臂和翻转铲斗。根据铲斗容量1.6 m3和宽度1 800 mm,得到铲斗的铲装截面积为0.82 m2。根据40°～45°堆料安息角,得到料堆的坡度为45°。

令二次曲线AB方程为:

y=k(x-a)2+b

(2)

A点为二次曲线的极值点,面积S为0.82 m2。

根据上述条件,可列出以下方程组:

(3)

式中:xO2为铲装起点;yA为水平插入终点竖直位置;fO2B、fO2A分别为料堆形状轮廓曲线、水平插入曲线。

根据计算出的数值解得k为2.468 2,a为3.691 9,b为-1.283 1。由此可得,地下铲运机铲装轨迹方程为:

(4)

5 数学建模

地下铲运机工作装置的执行机构为铲斗,为获取准确的铲斗运行轨迹,对铲斗斗刃进行运动轨迹分析。为了方便对铲斗斗刃进行运动学计算,将工作装置中的前车架、动臂、铲斗组成一个树形分枝[6-8],其坐标系如图4所示。

铲斗斗刃P点在参考基坐标系中的位置可以用相邻两刚体连体基坐标系之间的齐次坐标变换矩阵来描述。设A1为地下铲运机前车架在参考基坐标系中的运动位置,A2为动臂相对前车架的位置,A3为铲斗相对动臂的位置,AP为点P相对铲斗的位置,于是地下铲运机工作装置各连杆相对于参考基坐标系的位置可表示为:

(5)

利用多刚体运动学旋转变换矩阵理论,结合各刚体间的位置关系,进行矩阵变换:

(6)

(7)

(8)

(9)

联立式(5)～式(9),得到铲斗斗刃P点在参考基坐标系中的位置变换式:

RTP=A1A2A3AP=

(10)

式中:Si=sinθi;Ci=cosθi;Sij=sin(θi+θj);Cij=cos(θi+θj);Sijk=sin(θi+θj+θk);Cijk=cos(θi+θj+θk);Lij为铰链i、j之间的距离;θi为Xi+1与Xi之间的扭角,如果Zi的方向满足从Xi+1到Xi的右手螺旋定则,那么取正角度,否则取负角度。

在式(10)中,θ2、θ3分别为动臂油缸行程、转斗油缸行程的函数。考虑各树形分枝机构自身并不相互独立,列出相互之间的约束方程:

RTF=RT11T22TF=RT88T77TF

(11)

RTD=RT66T55TD=RT11T22T33T44TD

=RT11T22T99TD

(12)

式中:iTj为坐标系{j}原点在坐标系{i}中的坐标。

利用运动学方程的逆解进行求解,已知铲斗斗刃P点的位置,反求工作油缸的行程。设定铲斗的位置已知,则有:

(13)

式中:(nx,ny,nz)、(ox,oy,oz)、(ax,ay,az)依次为连体基坐标系的三个坐标轴在参考基坐标系R中的坐标;(px,py,pz)为连体基坐标系原点在参考基坐标系R中的坐标。

对地下铲运机实际铲装过程中铲斗斗刃等数据采样,利用式(11)和(12),得到100个对应的工作油缸行程值。经过计算处理后,进行曲线拟合,得到工作油缸的驱动函数。

转斗油缸和动臂油缸的驱动函数分别为:

(14)

(15)

式中:y1为转斗油缸相对于初始位置的长度;y2为动臂油缸相对于初始位置的长度;t为铲装时间。

对地下铲运机铲装插入过程进行速度取样,地下铲运机的速度规划为:

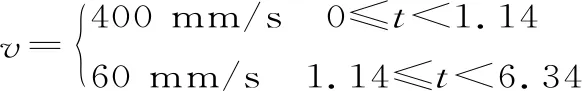
6 仿真分析

在铲斗斗刃与油缸行程函数关系已知的情况下,应用MATLAB/Simulink软件进行仿真计算,并对理想铲装轨迹曲线与仿真曲线进行分析。

以地下铲运机铲装前的状态为初始状态,仿真铲装过程铲斗斗刃的运动轨迹。可以将铲装过程分为三个阶段:

(1) 铲斗已下放至铲装状态,地下铲运机前进,推动铲斗到达料堆;

(2) 铲斗在地下铲运机的推动下铲入料堆,铲装一定深度,然后举升铲斗和翻转铲斗;

(3) 地下铲运机开始后退,驶离料堆。

对于多刚体系统而言,各刚体之间是通过接头与运动副的方式连接起来的。笔者在导入地下铲运机工作装置的计算机辅助设计文件后,加上必要的驱动、约束和检测模块,完成系统的模型构建。地下铲运机工作装置各部件之间的运动副关系见表1。

仿真模型的建立除了需要机构之间的装配约束,还需要对前车架刚体和路面刚体建立驱动,这时需要单独添加的驱动模块。此外,还需要定义机械环境条件,如重力、加速度作用方向等。结合基于铲斗斗刃与油缸行程位置关系而得到的地下铲运机动臂油缸和转斗油缸驱动方程,建立铲斗的运动仿真模型,并与理想铲装轨迹曲线进行对比。

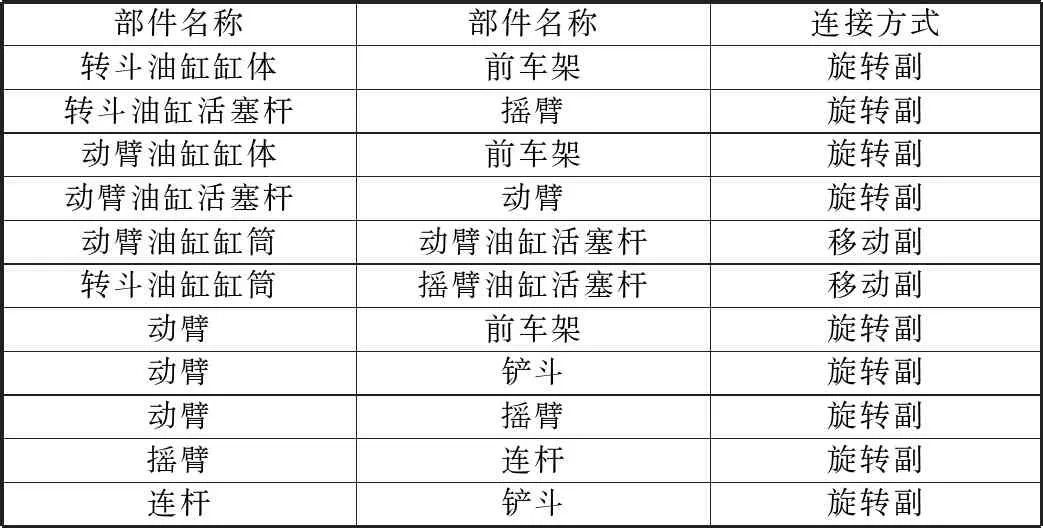
表1 地下铲运机部件之间运动副关系

获得仿真数据后,在MATLAB软件中绘制铲斗斗刃轨迹曲线,如图5所示。铲斗铲入料堆一定深度后,工作油缸和地下铲运机配合动作,完成铲装作业,然后地下铲运机驶离料堆。

▲图5 铲斗斗刃轨迹曲线

从图5中可以看出,两条轨迹曲线的趋势相同,但存在一定误差。从X值大于3 700 mm对理论铲装曲线和仿真铲斗铲装曲线进行竖直位移残差分析,如图6所示。

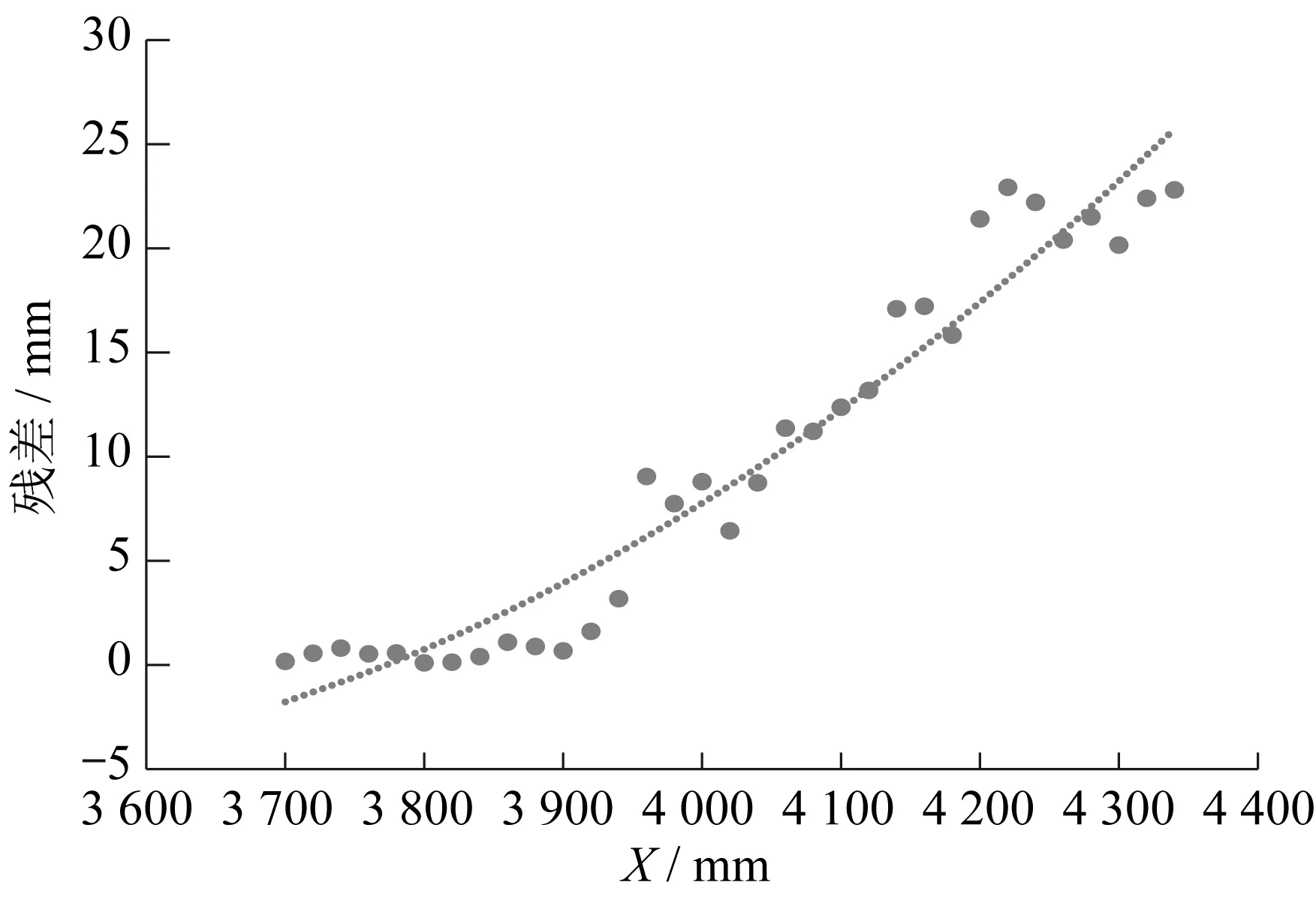
▲图6 竖直位移残差分布

从图6中可以看出,竖直方向位移的残差最大值为22.80 mm,残差呈现非线性递增规律,说明其中存在非线性系统误差。造成铲斗轨迹竖直方向系统误差的原因主要有两个。第一,建立运动学数学模型时所使用的设计尺寸与地下铲运机实际尺寸之间存在加工误差。第二,在地下铲运机仿真建模时,某些约束设置太过理想化,参数选取不够准确。

针对竖直方向的系统误差,除改进仿真模型参数设置外,还应采用修正法来进行误差消除。针对残差呈现非线性的特点,可以采用使系统误差随机化的组合测量法,或通过最小二乘法进行非线性系统数学模型构造,并进行实验回归统计分析,对系统误差进行补偿和修正。通过补偿修正后的铲斗斗刃轨迹曲线对比如图7所示,竖直位移残差分布如图8所示。可以看出,理想铲装曲线与仿真铲装曲线基本吻合,残差很小,对于地下铲运机的控制而言,误差可以接受。

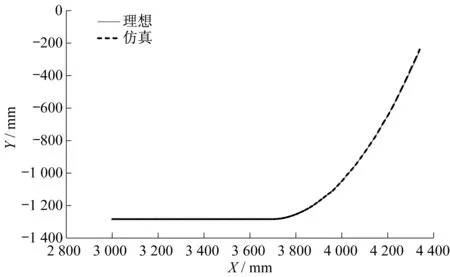
▲图7 补偿修正后铲斗斗刃轨迹曲线

▲图8 补偿修正后竖直位移残差分布

7 结束语

笔者在选定铲装方式和料堆形状轮廓后,规划出地下铲运机理想铲装曲线,利用多刚体系统分析方法,建立地下铲运机工作装置的运动学模型,推导铲斗斗刃位置与动臂油缸行程和转斗油缸行程之间的函数关系,解算出对应的动臂油缸和转斗油缸驱动方程。建立工作装置的MATLAB仿真模型,完成目标铲装曲线与仿真铲装曲线的误差分析,利用非线性回归分析进行补偿和修正,在误差允许范围内实现目标铲装曲线。所做研究对后续地下铲运机自主铲装控制器的设计具有指导意义。