基于DNN改性沥青中SBS含量的预测模型
2021-07-07王志祥李建阁
王志祥, 李建阁
(1.长安大学 公路学院, 陕西 西安 710064; 2.广东华路交通科技有限公司, 广东 广州 510420)
苯乙烯-丁二烯-苯乙烯嵌段共聚物(SBS)改性沥青路面有效减少了车辙、坑槽、裂缝等早期病害的出现[1-2],增加了1~2 a使用寿命,提高了服务水平,因此SBS改性沥青的研究及应用备受青睐[3-4].SBS用量的剧增,导致了其价格上涨,以次充好、缺斤短两的现象偶有发生,使改性沥青中SBS的含量及其性能无法保证.传统评价SBS含量的方法主要基于改性沥青的储存稳定性,对其针入度、延度、软化点和黏度等物理性能进行测试,但该测试方法耗时长、准确性和重现性较差[5-6];采用荧光显微镜定量检测SBS含量,准确性较低[7];化学滴定方法虽然能够测试改性沥青中SBS的含量,但耗时长达2h,并且会释放有毒气体,危害试验人员身体健康[8];通过傅里叶变换红外光谱(FTIR)仪测定改性沥青的红外谱图[9],基于特征峰与SBS含量的线性相关性,建立不同SBS含量改性沥青标准曲线,可以测定改性沥青中SBS的含量[10],但是其制样的均匀性难以保证,红外光谱峰的识别与提取、数据处理繁琐且复杂,这给改性沥青中SBS含量的测定带来了困难[11].深度神经网络(DNN)在精准预测方面具有显著优势[12].基于DNN,本文提出了改性沥青中SBS含量的预测模型(DNN模型),旨在精准预测改性沥青中SBS的含量,提升沥青的质量,改善沥青路面的使用品质.
1 试验
1.1 原材料
沥青采用Shell-70#基质沥青(BA),其性能指标见表1.改性剂为韩国LG411星型SBS与LG501线型SBS的混合物,二者掺配比(1)文中涉及的比值、用量、含量等均为质量比或质量分数.为1∶1;SBS颗粒色泽光亮,粒度均匀,杂质含量较少,无明显黏聚性,其性能指标见表2.根据工程经验,采用工业硫磺稳定剂(用量为沥青质量的2‰)增强SBS与沥青之间的黏聚力,确保改性沥青的储存稳定性.
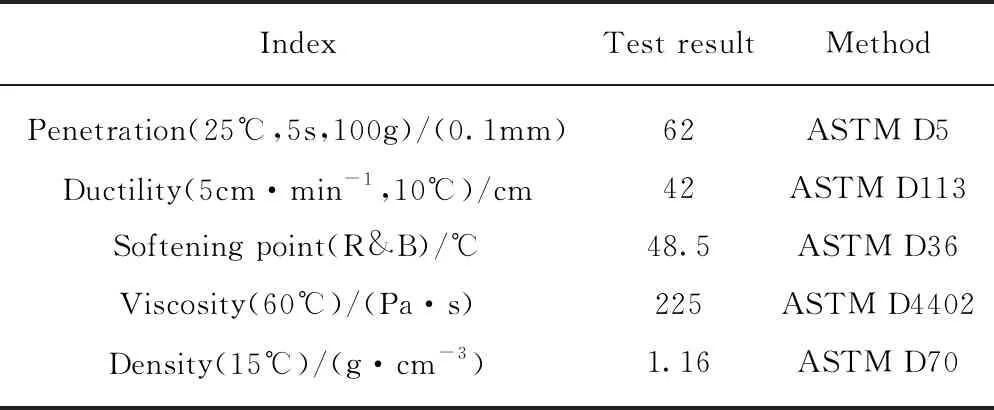
表1 基质沥青的性能指标
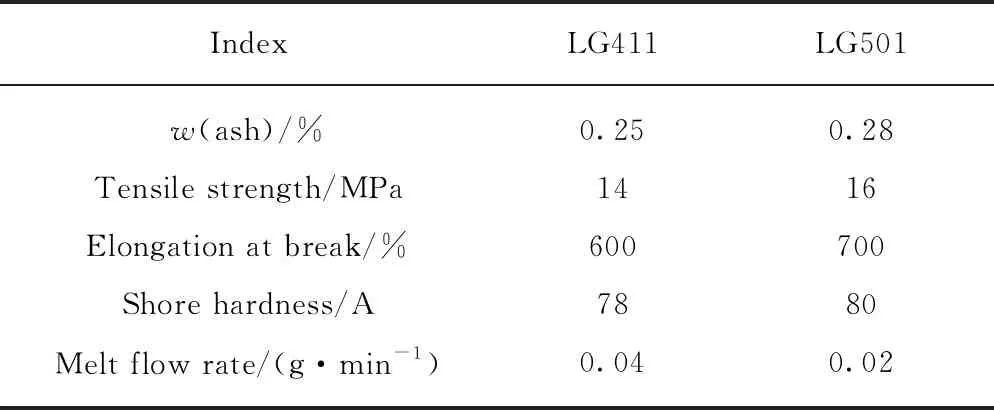
表2 SBS的性能指标
1.2 FTIR测试
采用配备ZnSe ATR附件的Controls Cary 630型FTIR,测试温度控制在20℃左右,光谱范围为4000~650cm-1,波数精度高于0.005cm-1,扫描次数为32次,分辨率为4cm-1.

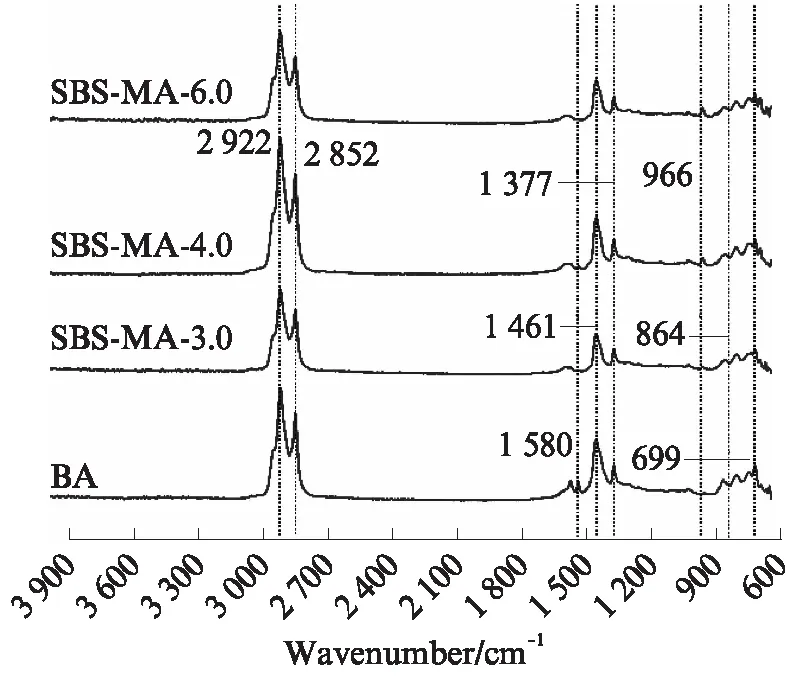
图1 基质沥青及SBS改性沥青的红外光谱图
2 DNN模型的建立
2.1 数据预处理
2.1.1降噪
制备7种SBS改性沥青和1种基质沥青的FTIR测试样品,每种样品30个,共得到240个样本.对其进行FTIR测试,得到240个FTIR图谱特征数据,并进行DNN训练与测试.FTIR图谱采用Savitzky-Golay过滤器进行平滑预处理,减少噪声干扰[14-15],同时对异常光谱进行剔除,得到227个有效FTIR图谱.随机抽取180个有效FTIR图谱作为DNN训练样本,样本编号为1~180,剩余的47个有效FTIR图谱作为DNN测试样本,样本编号为1~47.
2.1.2降维
每个FTIR图谱均包含900个特征(维度),227个图谱共有227×900个特征.采用奇异值分解算法对特征值数据的主成分进行降维,将输入数据转换成1组线性无关的特征值和相应的特征向量[16].在保留能够代表原始数据95%以上特征的前提下进行降维,最终得到227×512个特征数据.
2.2 数据分类
将降噪+降维后的数据作为DNN训练和测试样本的数据库,其样本信息见表3.表3中,N为数据预处理后的数据数量,Ntrain为用来训练的数据数量,Ntest为用来测试的数据数量.
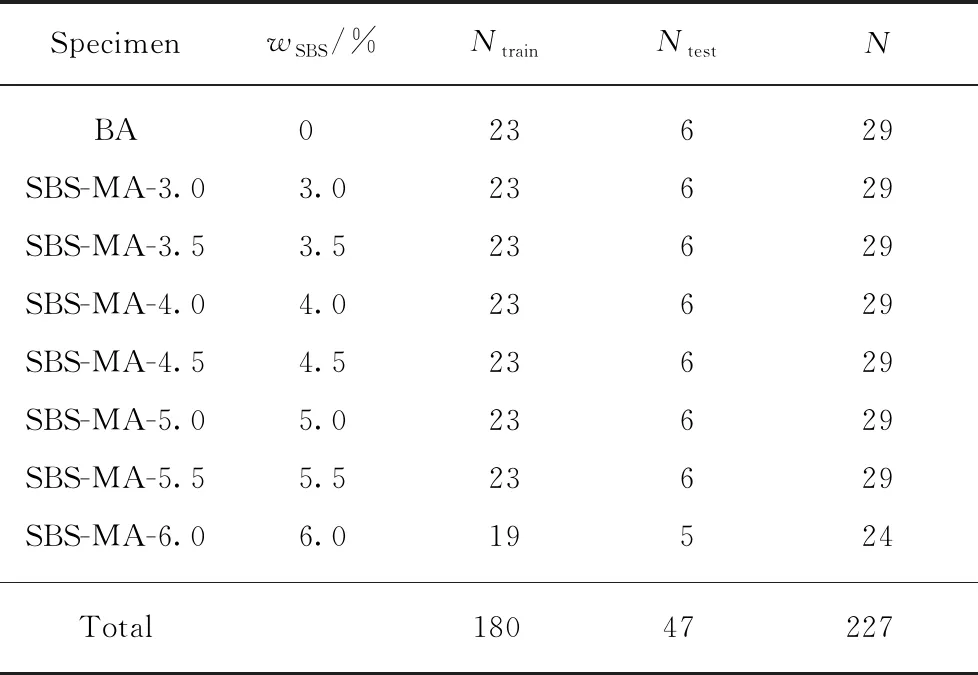
表3 数据库样本信息
2.3 DNN结构设计
为保证神经元直接快速并准确传递有效信息,对DNN结构进行设计,建立的DNN结构体系见图2.由图2可见:DNN由输入层、输出层和11个隐藏层组成,隐藏层从第2层到第12层依次排列,以提高学习的深度和模型表达能力;隐藏层神经元节点数分别设置为512、256、256、128、128、64、64、32、32、16和16,以提高计算机的处理效率,加快优化速度;同1层神经元之间没有联系,但它们与下1个相邻层的每个神经元完全相连;将式(1)中SBS改性沥青FTIR数据的特征向量X导入到包含512个神经元的输入层中;X(k)为X中的1个元素,为第k个样本FTIR数据的特征向量,k=1,2,3,…,m,m为样本数;根据输入值X,由式(3)计算得出SBS含量的输出特征向量Y.
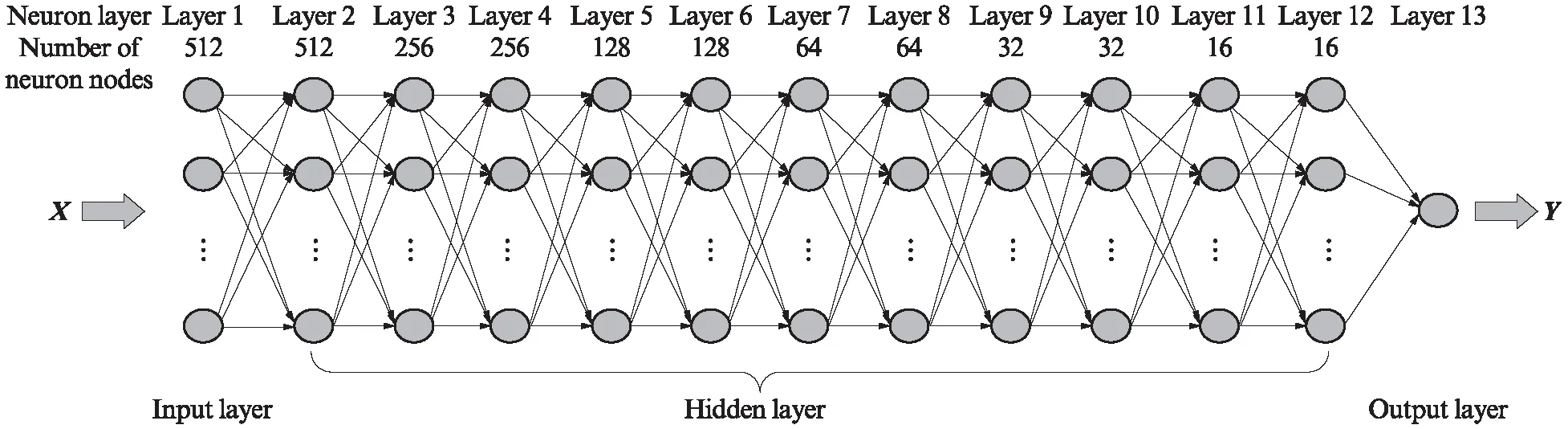
图2 DNN结构体系
X=(X(1),X(2),…,X(k),…,X(m))T
(1)
(2)
(3)
(4)
(5)
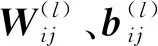
为避免在DNN的反向传播过程中出现梯度消失现象,提高计算速度和精度,同时降低DNN参数的依赖性与过度拟合的概率,采用ReLU(梯度总是0或1)作为激活函数[17]:
f(x)=ReLU(x)=max(0,x)
(6)
式中:x表示输入值;f(x)表示输出值.
2.4 DNN训练
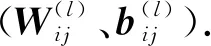
2.4.1损失函数
DNN训练通常采用损失函数J,使DNN模型输出特征向量Y的预测值与事先已知的用来监督预测模型的并和预测值相对应的真实值y(目标值)无限接近.用均方误差(MSE)作为损失函数J,并以MSE作为模型预测精度的评价指标,MSE值越小,模型预测精度越高.MSE的计算公式为:
(7)
2.4.2学习方法
学习在DNN训练中起着关键作用.学习过程为:首先将预处理后的数据以矩阵的形式输入到DNN中,进行无监督学习,该过程为前向传播中的特征学习,权重和偏差特征向量的初始值用于训练第1层并生成用于训练第2层的特征向量数据;依次利用产生的特征向量数据对下1层进行训练,直到最后1层完成训练后,得到各层相应的权重和偏差特征向量数据;最后对数据标记后进行监督学习,以调整DNN参数的权重和偏差特征向量.依据损失函数,采用小批量随机梯度下降法对每次迭代的参数进行更新,设置batch size为20,参数更新如式(8)、(9)所示.
(8)
(9)
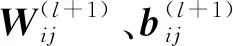
2.4.3初始化、规范化和归一化
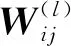
(10)
式中:ninput和noutput分别为输入、输出层连接的神经元个数.
为了降低DNN训练过程中过拟合出现的概率,常采dropout对DNN进行规范化,在每次迭代中,随机隐藏一半的神经元,在正向和反向传播中,隐藏的神经元都不会被激活.
通过批量归一化,固定输入层数据,优化求解过程,确保梯度稳定,加快收敛速度和学习速度,防止梯度消失.特征向量X与矩阵特征值Z之间的关系为:
(11)
式中:μ、σ分别为特征向量X中批量数据的平均值和标准差;γ、β分别为由DNN训练得到的尺度因子和位移因子;ζ为平滑因子,为无穷小的数字,防止除数为零.
2.4.4DNN模型的效率
本文使用的计算机处理器为Inter(R)core(TM) i7-8700 CPU@3.20GHz,显卡类型为Nvidia Geforce GTX 10708G GPU.通过CPU加速对DNN进行训练,前向传播学习和后向反馈学习时间分别为8.22、25.37s.
2.5 DNN测试
DNN测试的目的是分析预测模型准确性.采用测试样本进行DNN测试,若测试样本的均方误差小于训练样本,说明模型预测准确性较好;否则,应重新调整网络结构及其参数,直至测试样本的均方误差小于训练样本为止.
3 结果与讨论
3.1 数据预处理对DNN模型预测精度的影响
其他条件相同,以MSE作为评价指标,研究了降噪+降维、仅降维、仅降噪3种数据预处理对DNN模型预测精度的影响,结果见表4.

表4 数据预处理对DNN模型预测精度的影响
由表4可见,对比没有经过数据预处理的DNN模型预测精度,仅降维预处理使MSE降低了6%左右,而仅降噪预处理使MSE降低了64%,降维+降噪预处理的综合作用使MSE降低了70%,因此数据的降维、降噪等预处理对建立较为精确、鲁棒性较好的预测模型有重要的作用.
3.2 迭代次数对DNN模型预测精度的影响
对训练样本集设置不同的迭代次数(Nlit),研究其对模型预测精度的影响,结果见图3.由图3可见:随着训练样本集的迭代次数从100次增加到3000 次,DNN模型的MSE逐渐减小,从3.338减小到0.057;前1800次迭代,MSE波动较为明显,单次的迭代不一定使神经网络向目标方向发展,但是整体趋向目标,通过反复迭代,调整权重和偏差,使网络逐渐稳定;当迭代次数从1800次增加到2100 次,MSE缓慢下降,保持稳定在0.057;当迭代次数从2100次增加到3000次,MSE呈现小幅度波动.考虑训练速度,迭代次数选择2100次.
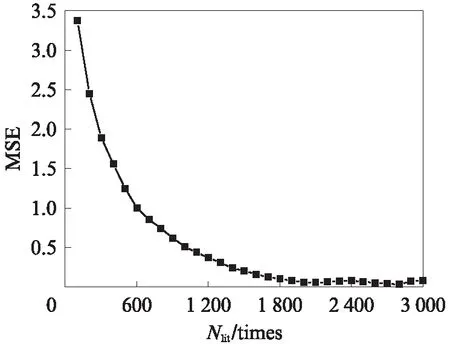
图3 迭代次数对DNN模型预测精度的影响
3.3 DNN模型预测结果分析
对数据进行降维+降噪处理,迭代次数为2100次.训练样本与测试样本wSBS的预测值(PV)与目标值(TV)见图4、5.由图4可见:训练样本的预测值在目标值附近小幅波动;样本编号为100之前,预测值与目标值基本呈现正偏差状态;样本编号在100之后,预测值与目标值出现负偏差,且呈小幅波动整体稳定状态.由图5可见:测试样本的预测值在目标值附近小幅波动,wSBS的预测值稳定在目标值附近.
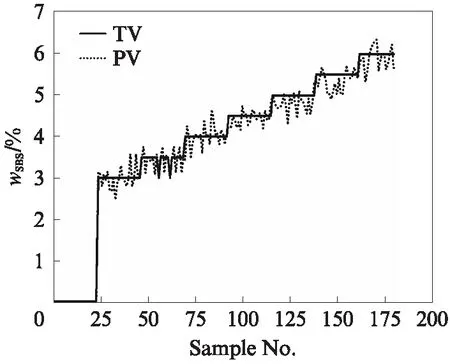
图4 训练样本的预测值与目标值
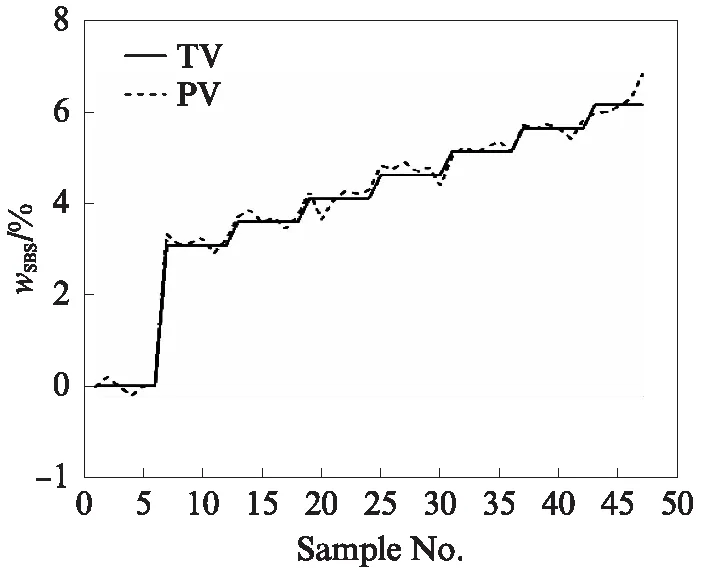
图5 测试样本的预测值与目标值
为进一步评价DNN模型的拟合优度,将训练样本集和测试样本集中SBS改性沥青的wSBS预测平均值与目标值进行相关性分析,结果见图6.由图6 可见,wSBS预测值的平均值与目标值相关系数R2达到0.9989,而测试样本预测值的平均值与目标值相关性更好,R2达到0.9996,这也说明了DNN模型的准确性和适用性,通过预测平均值的计算,可以使预测值逼近目标值.
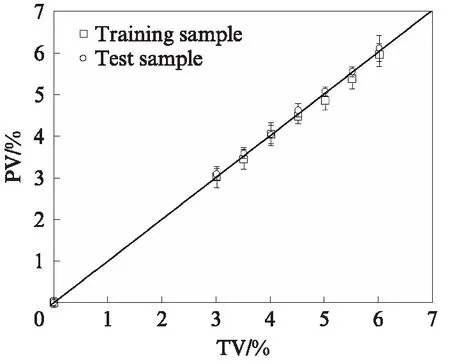
图6 不同SBS含量的预测值的平均值与目标值的相关性分析
3.4 精度对比分析
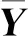
(12)
由表5可见:DNN模型的预测平均值与目标值线性相关系数R2为0.9989,模型预测精度优于SCM和RFM模型;对于同一目标值wSBS=4.7%的样本,RFM模型精度优于SCM模型,而DNN模型具有更高的精度,达到98.756%.一方面,说明了DNN模型可以准确预测不局限于预测模型训练集中的wSBS(3.0%、3.5%、4.0%、4.5%、5.0%、5.5%、6.0%),且能预测wSBS为3.0%~6.0%区间任意含量值;另一方面,也说明了DNN模型的预测值更逼近目标值,wSBS目标值为4.3%、5.1%的样本测试结果具有相同的结论;wSBS目标值4.3%、4.7%、5.1%的样本测试精度中,wSBS=4.7%的样本测试精度最高,测试结果最为精确.
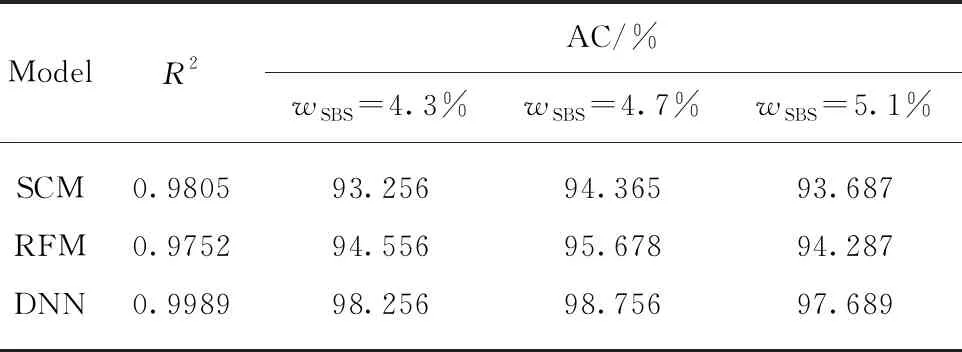
表5 3种预测模型预测精度比较
3.5 敏感性与适用性分析
为了验证DNN模型的敏感性与适用性,选择不同品牌和标号的基质沥青(Shell-70#、韩国SK-70#、新加坡IRPC-90#)、SBS(LG411、LG501、LCY3501、LCY3411)制备不同wSBS的SBS改性沥青,按照本文所述方法测试其FTIR图谱,同时用神经网络学习修正的DNN模型,对一定数量样本的验证集进行测定及精度评价,结果见表6.
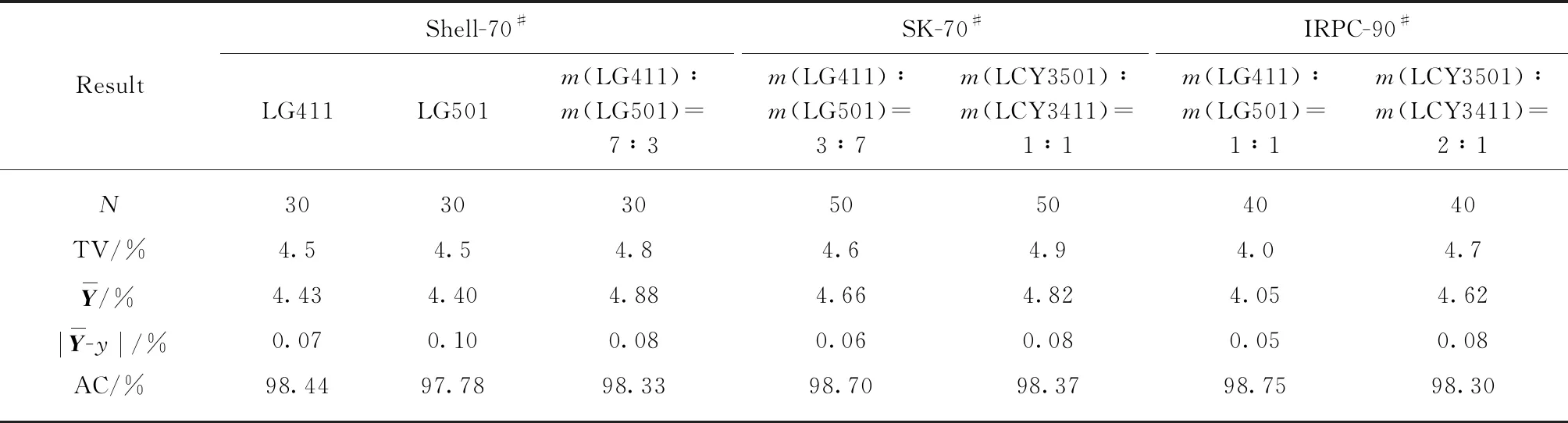
表6 不同改性沥青SBS含量结果
由表6可见:DNN模型能够准确预测不同基质沥青和SBS改性沥青中的SBS含量,且其预测值与目标值差值均在0.10%的范围内,精度最低为97.78%,最高为98.75%.由此可见,DNN模型具有很好的敏感性和适用性,能用于准确预测不同种类的SBS改性沥青中SBS含量.
4 结论
(1)在进行深度神经网络(DNN)训练之前,对数据进行降噪和降维等预处理,可以提高DNN模型的预测精度;相比于没有进行数据预处理,经过预处理的DNN模型的均方误差MSE降低了70%.
(2)训练样本集的MSE值最终保持在0.057,目标值与预测值接近,DNN模型具有良好的准确性.DNN模型对SBS改性沥青中SBS含量的预测精度在97%以上,高于标准曲线法和随机森林法.
(3)基于DNN改性沥青中SBS含量预测模型对不同基质沥青与SBS改性沥青中SBS含量预测具有较好的敏感性和适用性.
