面向城市飞行安全的无人机离散型多路径规划方法

胡莘婷，吴宇

1. 中国民航大学 空中交通管理学院，天津 300300

2. 重庆大学 航空航天学院，重庆 400044

由于无人机的运行对基础设施要求低、灵活性高，且具有能够精准完成“点”对“点”作业任务的优点，在城市中被广泛用于物流货运、航拍摄影、管线巡查、疫情防护等方面[1-3]，有效缓解了地面交通压力和提高了任务完成率，对公众生活产生了广泛影响[4]。在以上应用中，都需要为无人机规划一条从起点到终点的路径，保证无人机顺利完成任务。

为提高无人机的自主飞行能力，相关学者对于无人机在城市环境中运行的路径规划方法已进行部分研究。城市环境中障碍物数量众多且分布不均，无人机在运行过程中需要规避障碍物[5]，文献[6-8]将障碍物视为影响无人机运行的危险源，为避免无人机与障碍物相撞，研究了城市障碍物对无人机飞行路径的影响。除了以不可穿越的障碍物为研究对象以外，部分学者考虑到无人机在可穿越区域的运行风险，提出了基于风险规避的路径规划方法[9-11]。文献[9]研究了基于风险规避的离线和在线两种路径规划策略；文献[10]研究了无人机在城市环境中运行的风险因素；文献[11] 提出一种基于风险图的无人机四维航迹规划方法。

在城市环境无人机路径规划的算法方面，文献[6]提出了一种城市环境中小型无人机多障碍快速规划算法，对固定翼无人机运动学方程进行了合理简化，用螺旋线与直线组合构建近似最优航迹；文献[7]通过将航路规划分为全局规划和局部规划两个阶段, 使用A*算法进行全局路径规划引导无人机全局飞行, 使用广度优先算法和局部回溯思想综合进行局部航路规划。文献[8]针对城市空间的密集不规则障碍环境对无人机飞行安全的挑战，研究了面向城市环境的快速扩展随机树算法。然而，由于城市环境的复杂性，无人机飞行前很难获取全部的环境信息，并且考虑多架无人机同时在空中飞行时，可能会有冲突发生，使得规划出的一条路径不可用，导致该无人机的飞行任务被取消。在飞行计划阶段规划出多条备选路径，飞行时根据空中交通情况从多条备选路径中选择一条合适的路径，减少无人机飞行任务被取消的概率，是在保证安全的前提下增加空域容量的有效解决方案[12]。针对复杂环境下的多路径规划问题，文献[13-14]分别提出了基于加权K-均值聚类的粒子群算法和基于分级规划策略的A*算法。

城市环境中无人机的路径规划问题既要满足避障要求，又要考虑到无人机运行时对人产生的安全风险。上述研究缺少对避障和风险管理的综合考虑，且在安全性分析方面的研究不足。城市作为人们生产和生活的环境集合，人员密集。由于无人机运行时存在对地撞击的可能性，会对地面人员造成安全威胁，因此需要对地面人员建立风险分析模型[4,15-16]，并将其运用于无人机路径规划问题的研究中。在路径规划算法方面，已有的研究大都在连续型空间内以距离最短为目标，寻找一条最优路径，少有适合于离散型空间的多路径规划算法。因此，有必要提出一种面向城市飞行安全的无人机离散型多路径规划方法，使无人机在城市中运行既不与障碍物碰撞，又能减少对行人的安全风险，并且还能同时生成多条备选路径以提高无人机的任务完成率。

针对以上问题，本文研究离散型城市环境下的无人机多路径规划问题，根据定义的城市环境模型、无人机飞行规则和安全性原则，建立安全性分析模型和离散型多路径规划问题的数学模型；并对基本蚁群算法进行改进，提出改进聚类蚁群算法。本文的贡献主要有以下3点：

1) 本文考虑无人机在城市上空运行时对地面人员造成的安全威胁，综合人群密度、环境遮蔽等因素建立安全性分析模型。

2) 基于城市环境与无人机飞行规则，建立离散城市环境下无人机多路径规划数学模型，包括无人机飞行范围、障碍物规避准则、航路间差异的定义等。

3) 针对基本蚁群算法收敛速度慢、易陷入局部最优的缺点，对基本蚁群算法进行改进，设计聚类算子，提出改进聚类蚁群算法，使其能够同时产生多条安全性较高的路径。

1 多路径规划模型

本文对无人机离散型多路径规划模型的3个关键要素——决策变量、适应度函数和约束条件做如下研究。本问题中，根据定义的城市环境模型，决策变量为无人机飞行途经的航路点；与安全性原则相对应的，适应度函数为与安全风险相关的表达式；设计无人机飞行规则，并据此制定相应的约束条件。

1.1 城市环境模型和无人机飞行规则

本文将城市空域环境网格化为尺寸相同的正方体，构建无人机城市飞行环境三维模型。无人机朝着正方体的各个顶点飞行，飞行航段由正方体的边、面对角线或体对角线组成，如图1所示。

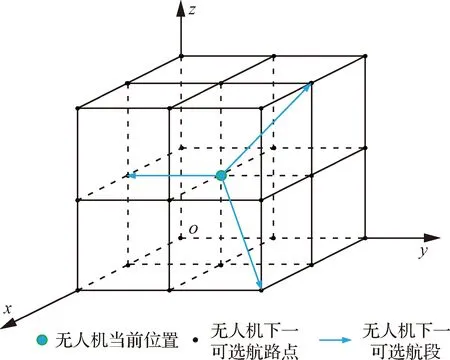
图1 无人机飞行规则示意图

与无人机当前位置相邻的航路点有26个，无人机每次位移均为沿着由相邻航路点连接的航段直线飞行。因无人机在城市飞行过程中需规避障碍物，故每次位移的可选航路点可能小于26个。

1.2 安全性分析模型

目前无人机飞行安全性分析的主流研究方法是以事故致死率作为衡量指标[17-19]：文献[17]搜集整理了国际上常用的无人机对地撞击风险评判标准，指出以无人机坠机导致的地面人员致死率作为其运行风险的衡量指标。在此基础上，相关研究者对无人机坠落致死情形展开了研究，文献[18]通过实验研究了无人机坠落时的重量和高度与事故致死率之间的关系；文献[19]考虑了环境遮蔽对无人机坠机事故的影响程度，建立了行人受撞击致死概率的数学表达式。本文基于以上考虑建立以事故致死情形为评判标准的安全性分析模型。设无人机在人群上空高度为h处飞行，如图2所示。

图2 无人机对地面人群的安全威胁

本文将无人机危害地面人员生命安全的事故发生过程分为3个阶段：① 无人机在人群上空运行时发生坠机，② 坠机砸中地面人员，③ 人员因受到强烈撞击而身亡。与上述3阶段对应的数学模型表达式为

R=PNF

(1)

式中：P为无人机每飞行1 h发生坠机的事故率；N为与无人机发生碰撞的人数，数值大小取决于坠落区域的人口密度，人群越密集，无人机对地撞击时砸中人的概率越大，风险越高；F为地面人员受撞击时的致死率，致死率大小与碰撞动能有关。基于此，地面人群上方空域无人机飞行安全性分析模型的建立过程如下。

与无人机发生碰撞的人数N与坠落区域的人口密度正相关

N=AρH

(2)

式中：A为无人机对地撞击时的面积分量；ρH为无人机坠落区域的人口密度。

无人机的质量越大、飞行高度越高，根据动能定理，对地撞击时的动能越大，造成地面人员死亡的可能性越高，风险越高，反之亦然。同时考虑到城市环境中存在的建筑物和树木等，它们在无人机坠机时会对地面人员产生遮蔽和缓冲的作用。因此综合考虑无人机撞击动能和环境遮蔽的影响，Dalamagkidis等[19]建立了撞击致死概率F的定量表达式

(3)

式中：S为遮蔽指数，对应于地面人群的暴露程度，借鉴Primatesta等[10]的研究，遮蔽指数取值如表1所示；λ为S=0.5时致死率达50%所需的撞击能量；μ为当S趋于0时致死所需的撞击能量阈值。E为碰撞动能，结合文献[19]的研究，通过式(4)可求得。

表1 遮蔽指数

(4)

式中：m为无人机的质量；g为重力加速度；q为阻力系数；ρA为空气密度。式(3)和式(4)表明无人机事故致死率与无人机的飞行高度呈正相关关系。

1.3 适应度函数

城市环境对无人机运行而言可分为如下两类：① 障碍物占据的空间为不可穿越区域，无人机须与之保持一定的安全距离，通过绕行的方式规避碰撞风险；② 无障碍物占用的空间为无人机可穿越区域，但无人机在可穿越区域飞行时需考虑其对地面人员造成的安全威胁。为使无人机在不与障碍物发生碰撞的前提下，尽可能降低运行时产生的安全风险，适应度函数定义为与风险有关的表达式。

为突出不同区域的风险差异，引入比例因子ω调整式(1)数量级，将一个区域内的风险表示为

C=ωR

(5)

按照1.1节所述的城市环境模型，可对城市空域内各正方体区域的风险进行量化，表示为

(6)

式中：(m,n,l)为图1所示的城市环境模型中各正方体的位置编号。

无人机飞行路径的信息可表示为

(7)

进而本文从安全风险角度建立适应度函数为

(8)

式中：CL为无人机飞行路径L的总风险，其值为无人机途径各区域风险值的加和，总风险值越低的路径越优。

1.4 约束条件

根据1.1节描述的城市环境模型和无人机飞行规则，制定如下约束条件。

1) 无人机飞行范围的约束

无人机飞行经过的每个航路点都必须位于指定的空域范围内，即

(9)

式中：xmin、xmax、ymin、ymax、zmin、zmax分别为城市空域的边界范围；a为正方体的边长；xi、yj、zk为无人机可选的航路点坐标集。

为提高模型的计算速度、缩小航路点的搜索范围，可将式(9)转化为

(10)

式中：XU=min {xmax,(xNmax+ab)}和XL=max {xmin,(x1-ab)}分别为无人机可飞空域在x轴方向的上/下界，x1和xNmax分别为无人机飞行任务在x轴方向的起/终点坐标，同理可得y轴和z轴方向的参数符号；b为扩张系数，使无人机可飞空域由原起/终点为界所围的立方体沿各轴方向各扩大2ab的长度。

2) 无人机避免与障碍物相撞的约束

无人机途经各航路点与障碍物边缘的距离应不小于正方体边长a，避免与障碍物碰撞。

(11)

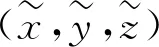
3) 无人机飞行路径不折返的约束

任一条完整路径所经过的各航路点均不重复。航路点重复表明无人机飞行过程出现折返现象，所生成的路径必不是最优路线。

(xn1,yn1,zn1)≠(xn2,yn2,zn2)

(12)

式中：n1、n2为同一条路径中的两个航路点。

4) 无人机飞行路径长度的约束

受无人机续航能力的限制，为避免出现路径长度过长的情况，需要对无人机的路径长度做出约束。该约束条件可表示为对途经航路点数量的限制。任意一条完整路径所经过的航路点总数应不超过限制的最大数量

Nmax≤Npermit

(13)

式中：Nmax为一条路径中的航路点总数；Npermit为一条路径限制的最大航路点数量。

5) 无人机多条备选路径差异程度的约束

无人机从起点飞至终点有多条路径可以实现，对于多路径规划问题，需要明确不同路径间的差异。任意两条不同路径的差异程度表示为其各航段风险差值的总和

(14)

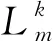
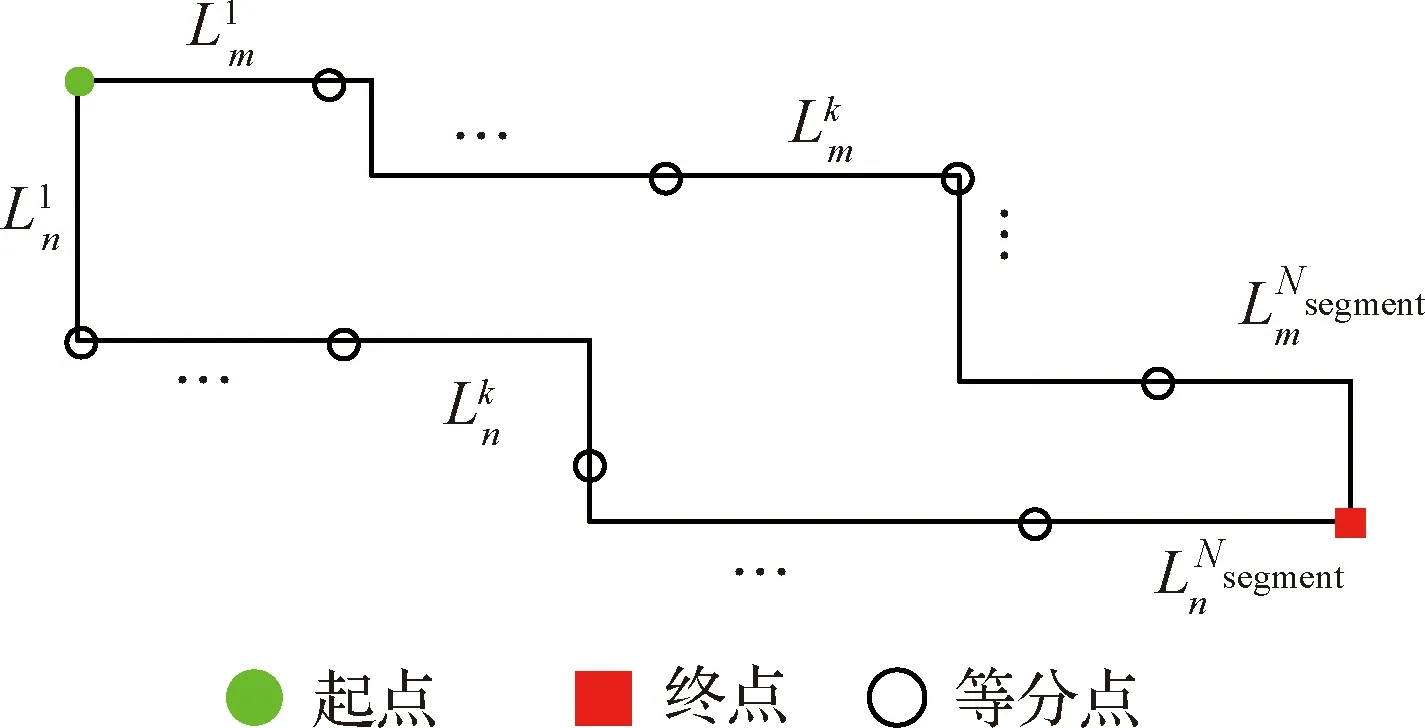
图3 不同路径的差异示意图

规定无人机多条备选路径间的差异程度需大于阈值DT，当DLm,Ln>DT时，视为两条路径具有明显差异。

2 多路径规划算法设计

首先对求解路径规划问题的算法进行选择。由于本文目标是同时获得多条路径，算法需要从多个初始解开始迭代，将聚类算法与群智能优化算法结合能够很好地实现上述要求。目前群智能优化算法多用于求解连续型优化问题，如差分进化算法、粒子群算法、人工蜂群算法等；但仍有少数的群智能优化算法适用于求解离散型优化问题，如遗传算法和蚁群算法。其中，遗传算法对决策变量的数量有一定要求，不易编码实现；因本文求解的各路径航路点数量不一，采用对航路点数量无要求的蚁群算法更为合适。

本节针对基本蚁群算法收敛速度慢、易陷入局部最优的缺陷，对蚁群算法进行改进。为了能够同时生成多条路径，设计聚类算子，与改进的蚁群算法结合，提出一种改进聚类蚁群算法。

2.1 改进的蚁群算法

为了提高标准蚁群算法(Ant Colony Optimization algorithm, ACO)的收敛速度和路径寻优能力，本文将对蚁群算法进行如下改进，提出改进的蚁群算法(Improved Ant Colony Optimization algorithm, IACO)。

1) 航路点的选择策略

从当前航路点转移到下一航路点时，蚁群算法在所有符合约束条件的备选航路点中，某个航路点被选中的概率由式(15)决定。

(15)

式中：pn(t)为航路点n在第t代被选中的概率；τn(t)为航路点n在第t代的信息素浓度；ηn为航路点n的启发项，标准蚁群算法的启发值为从该点到终点的距离的倒数；link为所有符合约束条件的备选航路点的集合；tmax为最大迭代次数；α和β分别为信息素因子和启发项因子，表示信息素浓度和启发值对航路点选择的重要程度。式(15) 表明备选航路点与终点的距离越短，该备选点被选中的概率越大。标准蚁群算法以寻求最短路径为导向，但从安全风险角度考虑，应使所求得路径的总风险较低。因此，与本文研究问题相对应的，将启发项改为

(16)

式中：Cn,x、Cn,y、Cn,z分别为从备选航路点到终点的x、y、z3个方向的风险预估值。上述设计的原理为从备选点中为无人机选择一个从当前位置到终点的安全性较高的位移方向，以使无人机沿着风险较低的路径飞行，提高无人机在城市环境中运行的安全性。

基于概率的航路点选择方法虽在一定程度上能避免路径搜索陷入局部最优，但同时也降低了算法的收敛速度。为解决此问题，本文通过随机轮盘赌的方式选择下一个航路点。引入随机数rand，规定当rand大于设置的阈值时，航路点的选择由式(15)确定，否则直接将被选择概率最高的备选航路点作为下一个航路点。本文在算法迭代的初期，设置较小的阈值，在迭代的后期设置较大的阈值。随机轮盘赌法是基于标准轮盘赌算法与贪婪算法的一种改良方法，该方法相较于标准轮盘赌法具有更快的收敛速度，同时又能克服贪婪算法易陷入局部最优的缺陷。

2) 算法参数自适应策略

一个好的优化算法应当在迭代初期具备较强的全局搜索能力，而在迭代的后期应有良好的局部搜索能力。标准蚁群算法中的信息素强度Q在迭代过程中保持不变，但设置为常数的Q并不能满足上述要求：较小的Q值会增加算法的全局搜索能力，但会降低收敛速度，而较大的Q则会因增加重复搜索到先前已经出现过的解的概率而陷入局部最优。因此，在算法迭代的初期设置Q为较小的值以避免算法陷入局部最优，并让Q值随着迭代次数的增加而增大，以增强算法的局部搜索能力，即

Q(t)=Q0+ln(t)c

(17)

式中：Q0为信息素强度初始值；c为信息素强度增长系数。

3) 信息素浓度更新策略

在当代路径生成完毕之后，标准的蚁群算法会对各路径所含航路点的信息素浓度进行更新，如式(18)所示。下一代的蚂蚁依据上一代蚂蚁留下的信息素进行路径点的选择。

(18)

式中：ρ为信息素浓度蒸发系数；Γa为蚂蚁a在第t代走过的航路点的集合；Δτa为信息素浓度增加值；CL(a)为蚂蚁a所走路径的总风险；s为种群规模。

为增强优质解的影响，本文对上述信息素浓度更新机制进行改进，在迭代初期，仅对当代最优航路所包含的航路点的信息素浓度进行更新；并且，为利于算法收敛，在迭代的后期仅更新历史最优航路所含航路点的信息素浓度。

此外，为防止因某个航路点的信息素大量堆积而导致算法陷入局部最优，本文将信息素浓度限制在一定范围内

τn(t)=max{τmin,min{τn(t),τmax}}

(19)

式中：τmax、τmin分别为信息素浓度的上、下限。

2.2 聚类算法设计

为了同时求解出多条路径，需要先通过聚类机制将具有明显差异的路径归为不同类别，在每个类别中，可行解随着蚁群算法的迭代过程朝着不同的进化方向不断更新和优化，最终获得具有一定差异的多条路径。

聚类的关键是确定聚类中心，合理的聚类中心能够加快算法的收敛速度，且能避免陷入局部最优。本文将初始路径按照风险值进行排序，选取风险值较低且差异明显的几条初始路径作为聚类中心，其他路径依据其与聚类中心的差异程度归类。聚类算法的流程如图4所示。

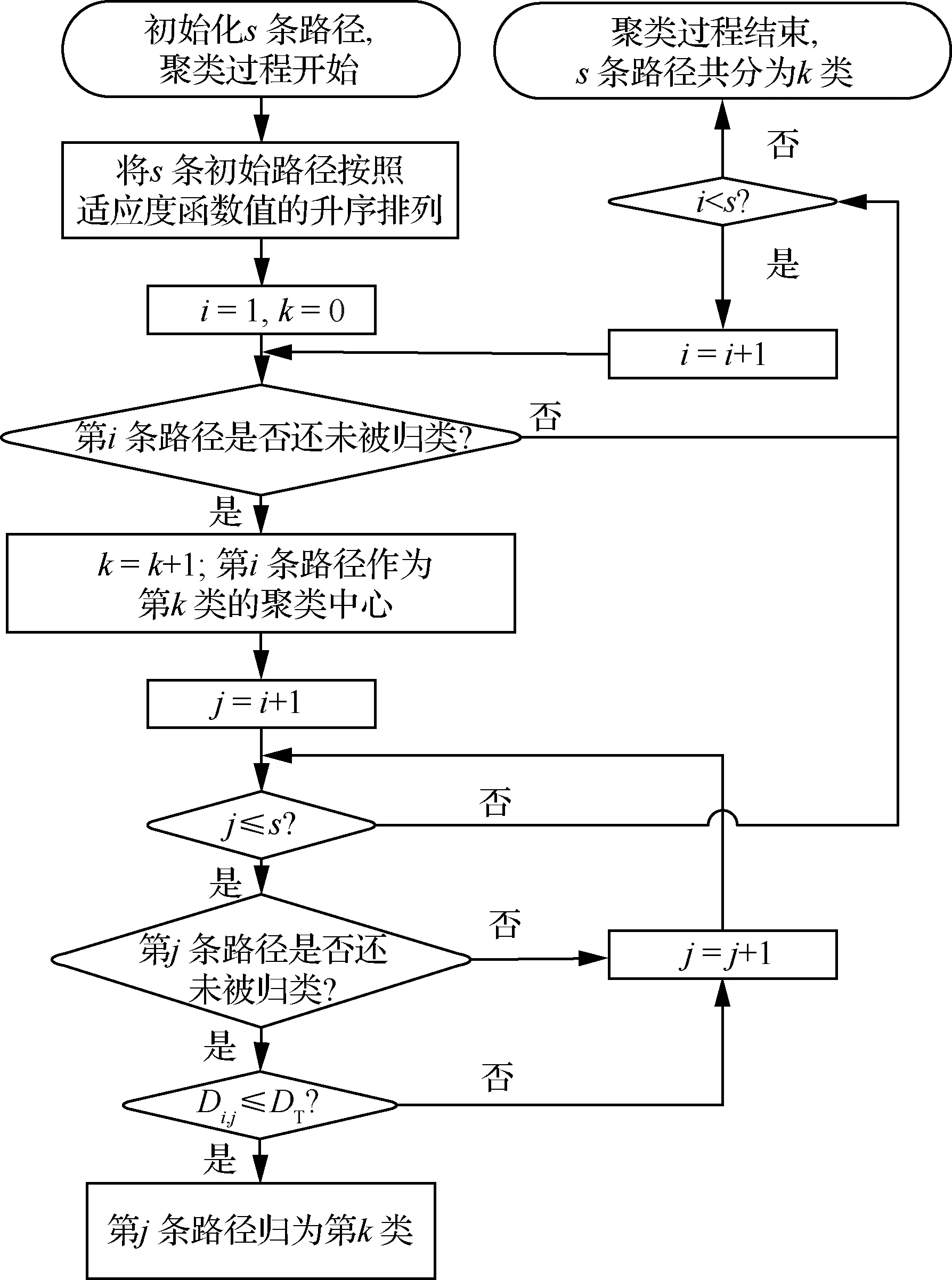
图4 聚类算法流程图

首先初始化s条路径，作为初始解。各初始解的适应度函数值由式(8)计算得出，并将其按照由小到大的方式排序。排序为第1的解作为第1类的聚类中心，排序为第2的解根据式(14)计算其与聚类中心的差异值，若差异值小于DT，则认为二者差异不大，将其归为第1类。排序在其后的解也按照同样的方法依次与排序第一的解进行比较，以判断是否归为第1类，直到初始解全部检测完毕。在所有未被归为第1类的解中，适应度函数值最低的解作为第2类的聚类中心。重复上述检测过程，直到所有解都归类完毕。

上述具有排挤机制的聚类过程具有如下特点：① 初始路径中适应度函数值较小且差异明显的几条路径作为聚类中心，使得每类中至少存在一条适应度函数值较小的路径，便于算法在后续迭代过程中获得较优的解，且利于算法收敛；② 类 别的数量不能提前确定，与初始路径的适应度函数值有关。与固定类别数量的聚类方法相比，自适应类别数量的聚类算法使得各聚类中心之间均有较大差异，为迭代过程奠定了不同的进化方向，能够保证算法最终输出的多条路径间的差异性。

2.3 改进聚类蚁群算法

常规的蚁群算法基于给定的适应度函数，通过种群迭代过程输出一个最优解。为能够同时生成多条备选路径，使无人机在复杂城市环境中能够顺利完成作业任务，本文将设计的聚类算子与改进的蚁群算法相结合，提出求解离散型多路径规划问题的改进聚类蚁群(Clustering Improved Ant Colony Optimization, CIACO)算法。算法流程如图5所示。

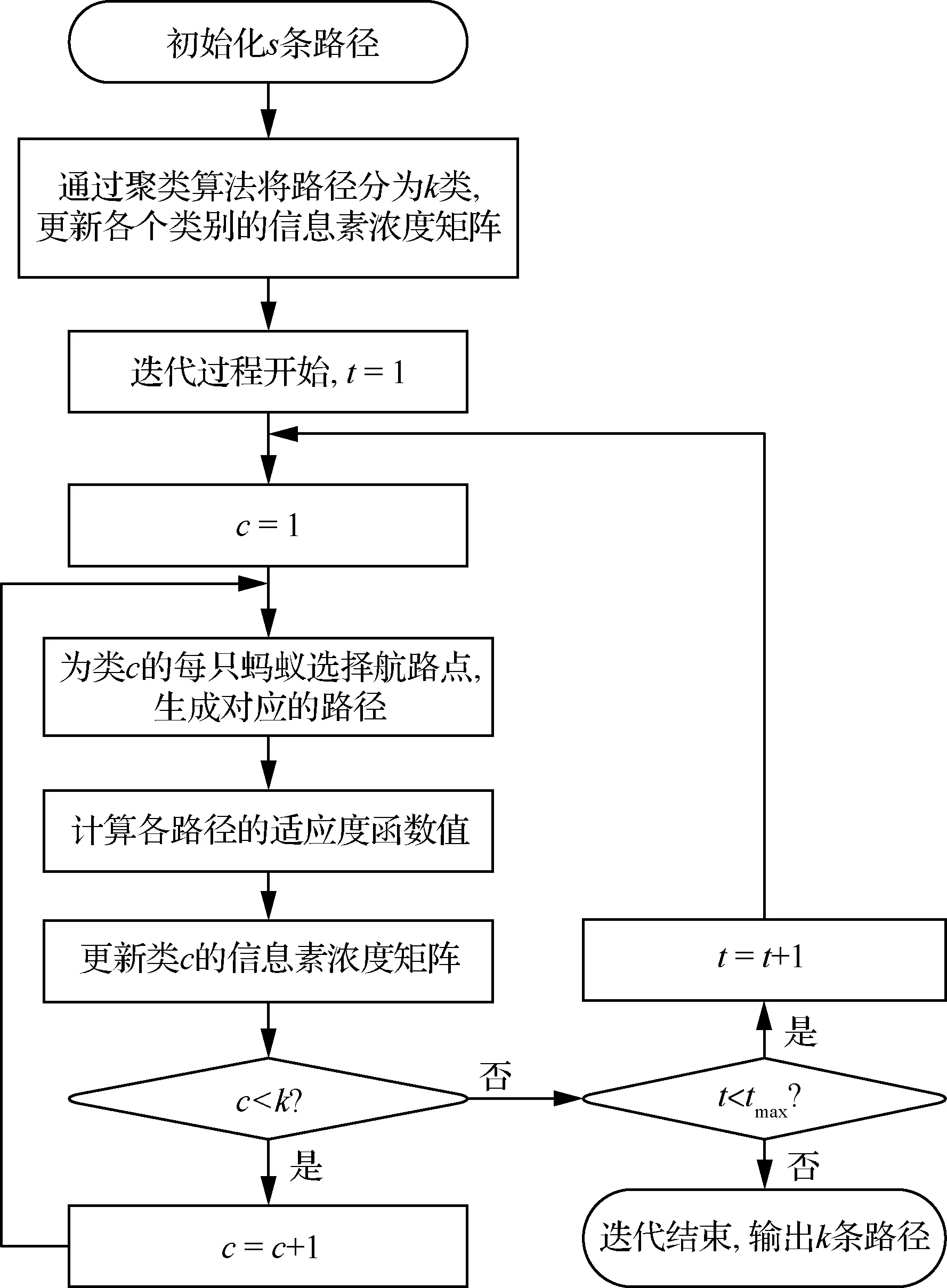
图5 改进聚类蚁群算法流程图

与标准蚁群算法不同，改进聚类蚁群算法在迭代前增加了初始化过程。初始化s条路径，计算各初始解的适应度函数值，将其按优劣次序排列。通过2.2节所述的具有排挤机制的聚类算法确定k个聚类中心，聚类中心为后续蚁群迭代过程指出大致的进化方向。聚类过程结束后按照类别更新各自的信息素浓度矩阵，迭代过程正式开始。与标准蚁群算法每次仅依据一个信息素浓度矩阵进行更新和进化不同的是，改进聚类蚁群算法有k个不同的信息素浓度矩阵。不同的信息素浓度矩阵在每次迭代过程中能够同时发挥作用，使得原本只能生成一条路径的蚁群算法最终能够同时输出多条路径。

结合2.1节改进的蚁群算法的第1)点航路点选择策略，按照类别分别为每只蚂蚁寻找一条可行路径，并计算其适应度函数值，寻路完毕之后依据第3)点信息素浓度更新策略更新各类别的信息素浓度矩阵。迭代过程中根据第2)点算法参数自适应策略动态更新信息素强度值。迭代过程结束后，每一类的最优路径，即该类适应度函数值最小的解，作为该类的最终结果输出。

3 仿真实验与结果分析

为验证本文提出的模型与算法在求解离散型城市环境下基于无人机飞行安全的多路径规划问题的合理性和有效性，分别进行如下仿真实验。首先搭建仿真环境，量化实验区域的风险值，在3.1节用本文以低风险为优化目标的方法与追求距离最短的方法对比，对本文所建风险模型的安全性和有效性进行分析；3.2节对比算法改进前后的性能，对算法改进的合理性进行分析。

3.1 风险模型合理性验证

设置实验空域在x、y、z方向上的范围分别为[0,1 800] m, [0,1 800] m和[0,90] m，正方体边长为30 m[20]，随机生成300个障碍物，人群密度为范围在[15×10-3,35×10-3]人/m2之间的随机数。根据常见的无人机机型大疆精灵4和文献[10,15,18,21]，风险模型相关参数的取值如表2所示，实验中用到的算法参数如表3所示，根据式(5)和表2参数生成的风险图如图6所示。

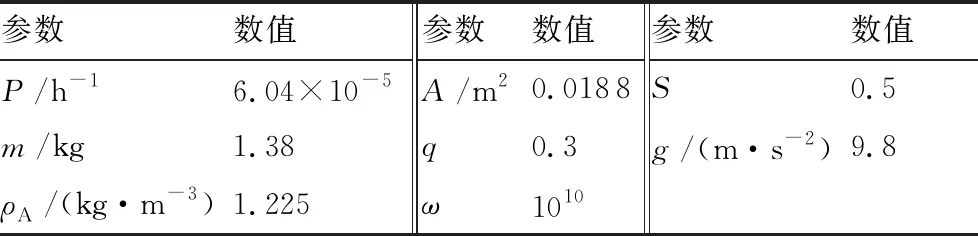
表2 风险模型参数

表3 蚁群算法参数表

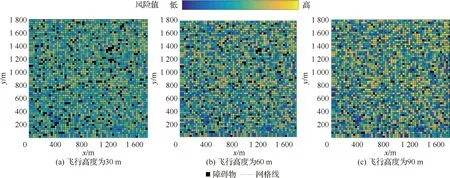
图6 各飞行高度层对应的风险图

在同样的城市环境模型和无人机飞行规则下，追求距离最短的方法与本文根据安全性原则设计的方法类似，二者模型的差别只在于适应度函数的设置上，其他的内容如决策变量、约束条件均相同。若以飞行距离为衡量指标，适应度函数值即为其路径的长度；路径间的差异值计算方法为同样将每条路径等分为Nsegment段，然后对两条路径对应等分点之间的距离求和作为其路径间的差异值。采用IACO算法对二者进行仿真实验，结果如图7所示。

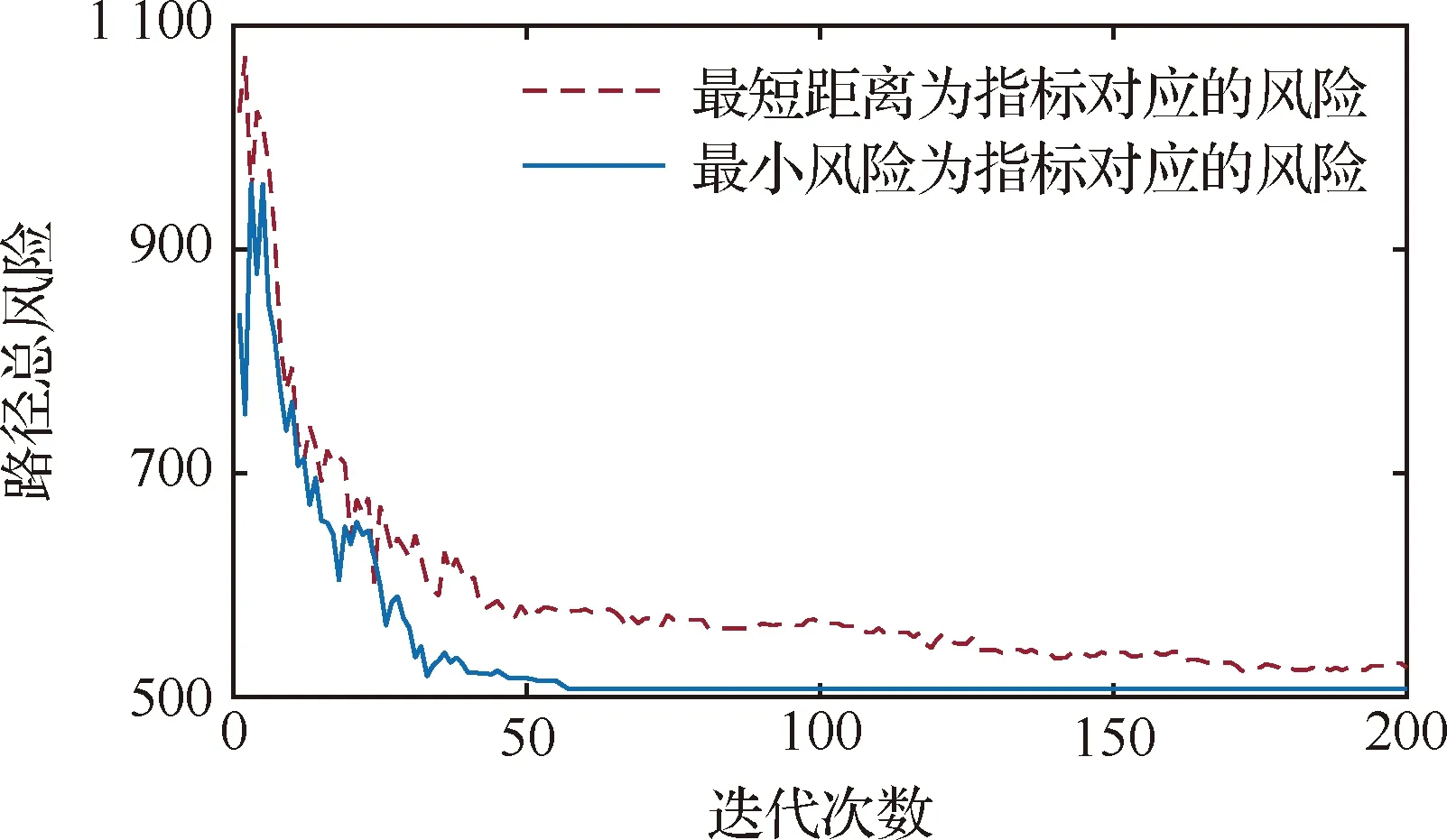
图7 IACO算法中两种指标下的风险对比

由图7可见，距离最短的路径不一定是最安全的飞行路径。以距离最短为寻优目标的路径规划方法，没有考虑到无人机运行时的风险，所求解出的路径风险值较高。根据本文所建的风险模型，以遵循安全性原则求解出的路径在安全性方面的表现具有明显优势。

3.2 不同路径规划算法的对比

分别用标准蚁群算法(ACO)、改进的蚁群算法(IACO)和改进聚类蚁群算法(CIACO)求解同一离散型多路径规划问题。在ACO算法基础上，按照第2.1节所述方法进行改进，得到IACO算法；IACO算法和CIACO算法的差别在于没有采用聚类机制，两种算法的其他内容均相同。根据仿真结果比较各算法在收敛速度、路径多样性和解的优质性上的差异。

空域搜索范围的扩张系数b取值为2，各路径限制的最大航路点数量Npermit=500，每条路径被等分为10段，即Nsegment=10，差异阈值DT=25。

设置起点(120,90,60) m，终点(1 590,1 620,90) m，Q0取为从起点到终点x、y、z3个方向风险预估值的总和，ACO算法中的信息素强度保持初值不变。信息素矩阵中所有元素初值设为1。ACO、IACO和CIACO 3种算法的对比结果如图8所示。

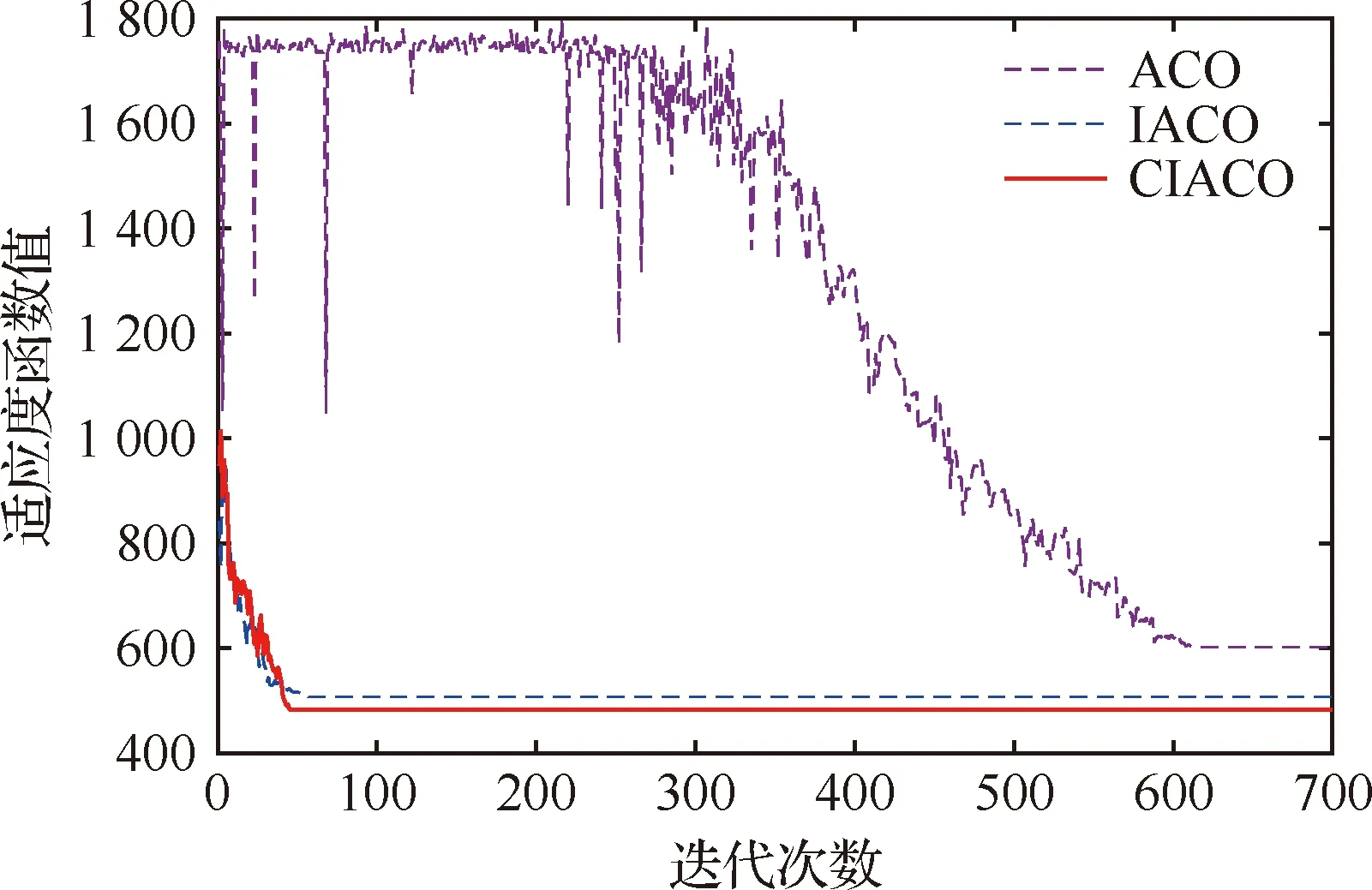
图8 3种算法的收敛曲线

从图8可以看出，ACO算法收敛速度缓慢，在经过614次迭代后才收敛，收敛时适应度函数值为602，远高于其他两种算法；IACO算法和CIACO算法收敛较快，分别在第57代和第47代达到收敛状态，且适应度函数值也较低，分别为507和482。

算法改进后收敛速度提升的原因是，本文在航路点的选择上以一定概率引导蚂蚁选择安全性较高的位移方向，避免因蚂蚁随机行走造成算法收敛缓慢；仅更新最优路径的信息素，避免下一代蚂蚁在根据以往蚂蚁留下的信息素进行路径搜索时受到历代质量不高的路径信息的影响；同时，所设计的自适应参数调整策略也能够对算法收敛起到促进作用。并且，因算法改进措施中对信息素浓度做了限幅操作，避免出现因某些航路点信息素大量堆积使算法重复搜索到已出现过的解，该策略提高了算法搜索到优质解的可能性。在采用本文第2.1节所述的策略对ACO算法进行改进之后，IACO和CIACO算法不论是在收敛速度还是在解的优质性上都相较ACO算法显示出了明显优势，证明了本文所提算法改进策略的有效性。此外，CIACO算法和IACO算法相比，之所以在迭代初期适应度函数值下降较慢、但在迭代后期产生质量更优的解，是因为聚类机制的使用使CIACO算法拥有多个进化方向，在迭代过程中解的搜索范围更大，导致适应度函数值下降较慢。但好处是使得改进后的CIACO算法更不易陷入局部最优，增加了算法搜索到优质解的可能性。

由ACO、IACO算法收敛生成的一条路径和由CIACO算法产生的多条路径分别如图9和图10所示。

如图9所示，ACO和IACO算法只能收敛得到一条路径，无法达到同时规划多条路径的要求。若想通过运行多次的方式获得多条路径，势必会占用过多的计算机运算资源，降低路径规划效率。与之相比，由图10可见，CIACO算法运行一次即能够产生多条路径。这是因为ACO和IACO算法没有聚类机制，在经过多次迭代后会收敛到一条路径；而CIACO算法在迭代开始之前，就通过聚类机制将初始解分类，随着迭代过程的进行，解能朝着不同的方向进化，最终达到同时输出多条路径的目的。CIACO算法各类别的收敛曲线如图11所示，3种算法的解的质量对比如表4所示。

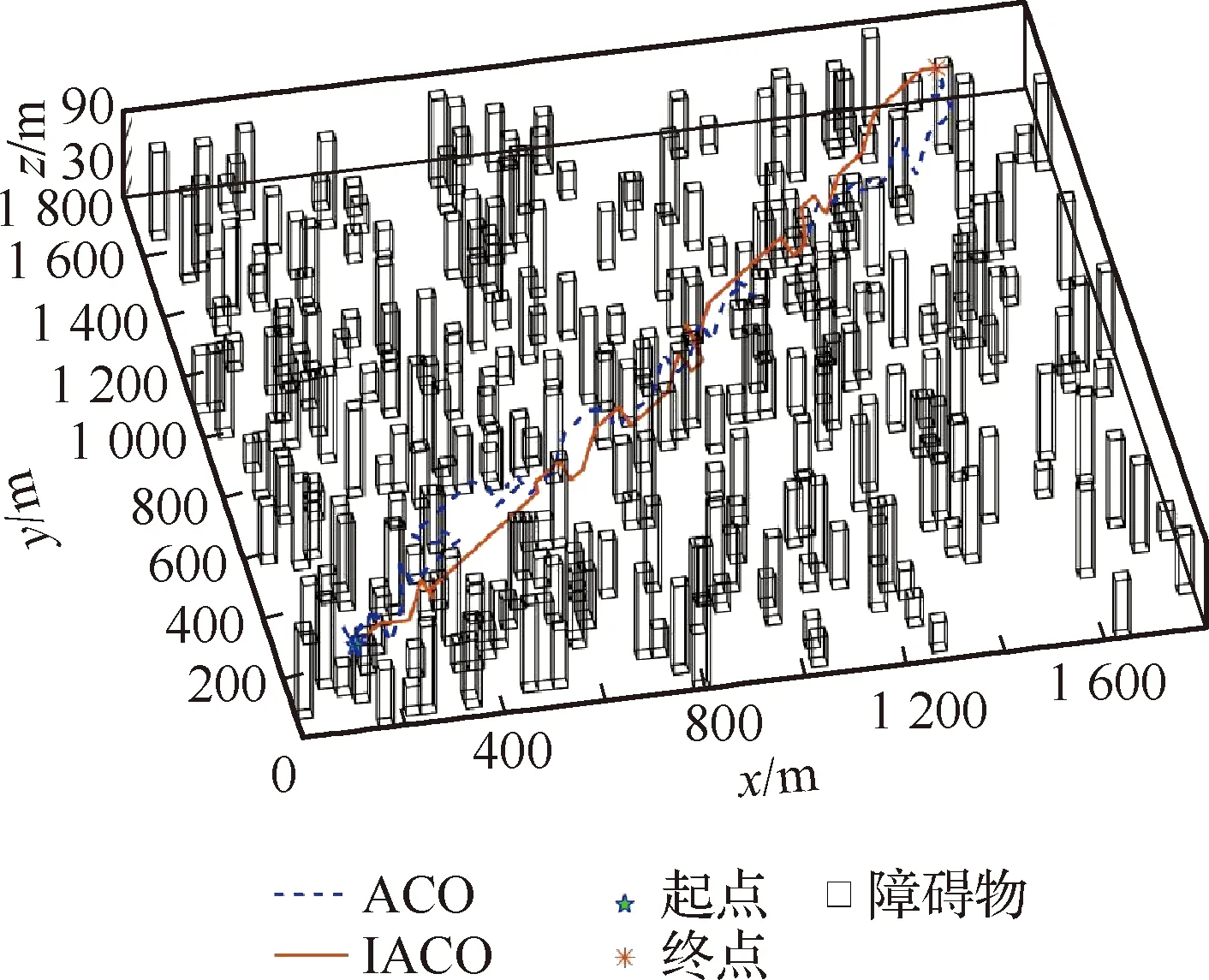
图9 ACO和IACO算法求解出的路径

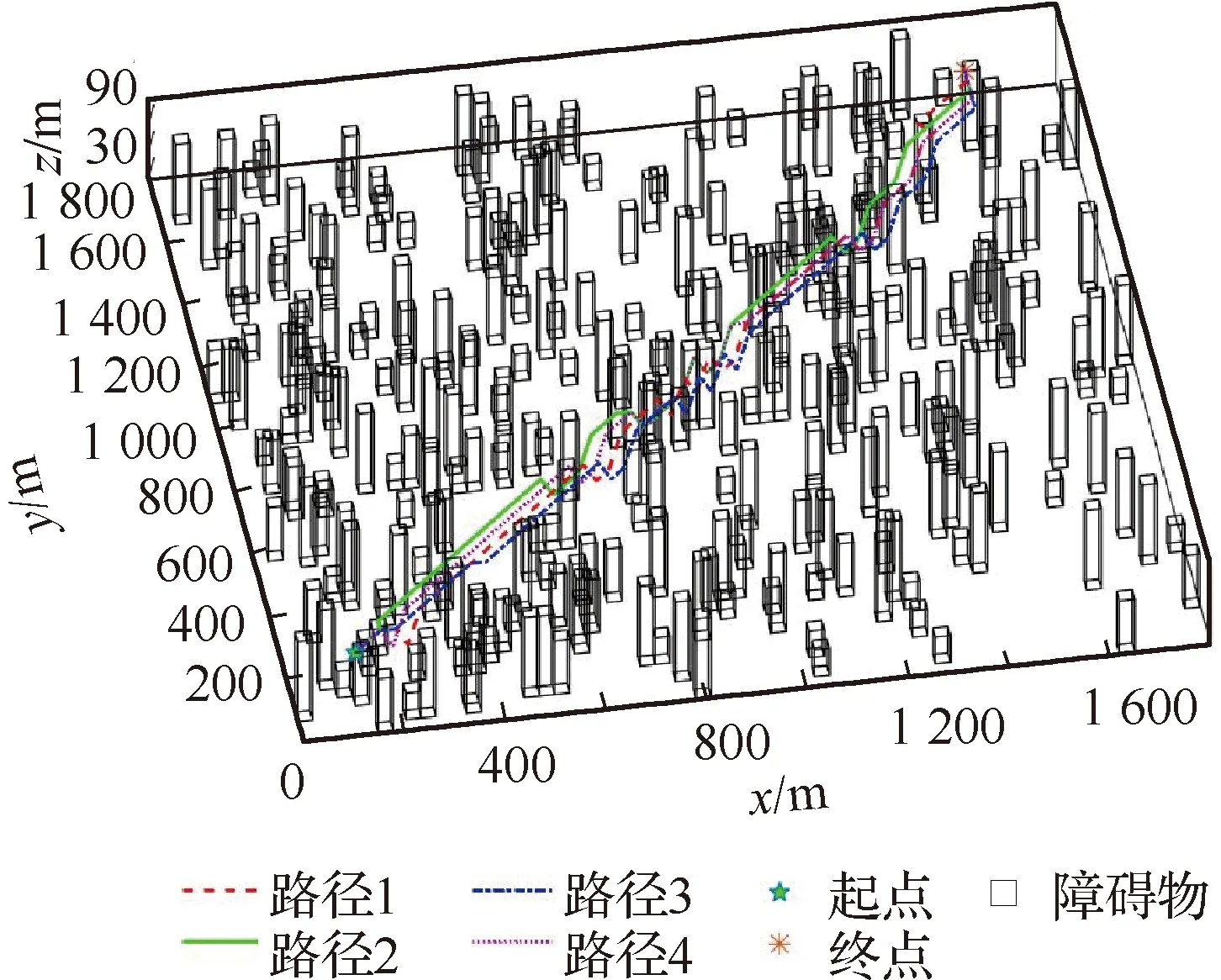
图10 CIACO算法求解出的路径

图11 CIACO算法各类别的收敛曲线

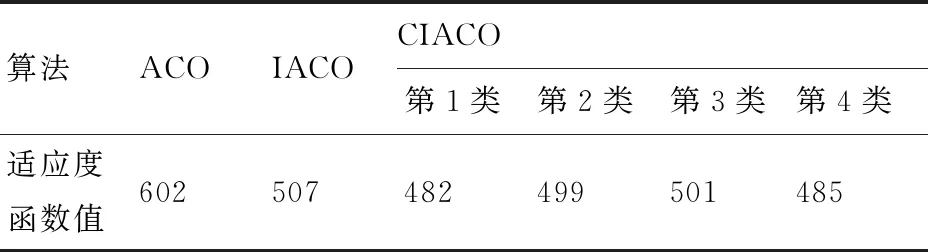
表4 3种算法解的质量对比

该算例中CIACO算法产生了4个聚类中心，最终输出了4条不同的路径。4条路径的适应度函数值最低为482、最高为501，均小于ACO与IACO算法生成路径的适应度函数值602和507。仿真结果证明了本文提出的CIACO算法不仅能同时生成多条路径，而且解的质量更优。

4 结 论

本文针对无人机在城市环境中的飞行安全和同时规划多条备选路径的需求，研究了面向城市飞行安全的无人机多路径规划问题。通过描述无人机运行风险的发生过程，建立安全性分析模型。根据定义的城市环境模型、无人机飞行规则和安全性原则，建立了离散城市环境下的无人机多路径规划数学模型。针对基本蚁群算法收敛速度慢、易陷入局部最优的缺陷，对蚁群算法进行了改进。设计聚类算子，与改进的蚁群算法结合，提出了改进聚类蚁群算法。通过仿真实验对比验证了本文所提方法不仅能够同时生成多条路径，为无人机飞行提供备选方案，而且所设计的改进聚类蚁群算法还具有收敛快、安全性高的优势。