基于QSS的自适应多步校正算法及其在柔性航天器动力学中的应用
2021-07-07李志华李广沈汉武樊志华
李志华,李广,沈汉武,樊志华
杭州电子科技大学 机械工程学院,杭州 310018
具有刚性、非线性和强耦合特点的动力学系统广泛存在于机械、土木、航空航天等领域。例如航天器系统,由于存在柔性件振动变形以及大范围运动位移和小范围振动位移之间的相互耦合,其动力学模型就呈现刚性、非线性和强耦合的特点[1-2]。对这类刚性系统进行仿真求解十分困难,而对其动力学模型的精确高效求解是对其进行精确控制的基础[3]。目前数值求解的方法主要包括直接数值求解法和降阶求解法。
直接数值求解法以Wilson-θ和Newmark为主[4-6],该方法需要调用迭代算法,计算成本高、仿真效率低,且仿真精度的提高存在局限性。降阶求解法通过将动力学方程转化为低阶的常微分方程,然后采用传统的数值积分方法进行求解,相比于直接数值求解法,它在仿真效率、计算成本以及仿真精度上均存在一定的优势。
降阶求解法所使用的传统数值积分方法有Euler法、Adams多步法、龙格库塔法和Gear法等。Euler和龙格库塔法属于单步法,Gear和Adams法属于多步法。其中,Euler法是最简单的数值方法,它在求解刚性问题时,需要显著地减少积分步长,以保持稳定性,但这会导致误差的积累,不利于刚性问题的求解;Gear法初始值较难确定,求解高振荡方程时会失效,同时方程的阶数一般较大[7];隐式的龙格库塔方法求解刚性问题时稳定性好、精度高,但是s阶的龙格库塔法在求解一个r维的刚性问题时,每步都需要求解一个由s×r个方程联立的方程组,在实际工程应用中,其计算量过于庞大,导致实际求解时的效率不高[8]。相比于龙格库塔方法,Adams多步法的优点是计算格式简单、每步计算量相对较小,同时也具备较高的求解精度,缺点是使用隐式Adams多步法在求解刚性问题时,相比于显式算法仍会有较大的计算量。由此可见,单纯地使用传统的隐式算法或显式算法来求解动力学中的刚性问题,都存在着一定的困难。
量化状态系统(Quantized State System,QSS)算法是一种新的数值积分方法,由Zeigler和Lee[9]首次提出,并由 Kofman和Junco[10]首次算法实现。与基于时间离散的传统方法不同,QSS将所有的状态变量离散化,以“量子”代替“步长”,通过计算所有状态变量每次变化一个量子所需要的最短时间,来进行下一步积分的推进。在求解非刚性问题时,QSS算法稳定性强,同时计算过程不需要迭代,因此仿真效率得到了极大的提高。QSS的状态变量轨迹是分段线性的,其求解精度相对于传统算法并不占优势。为了提高其算法精度,QSS2和QSS3采用高次曲线来对状态变量变化的时间进行估计,利用状态变量的高阶导数来改进近似值[11-13]。在求解非刚性问题时,QSS2和QSS3的求解精度得到了提高,要好于QSS。但在求解刚性问题时,QSS、QSS2、QSS3均存在可能的数值振荡现象;此外,在求解刚性问题时,QSS2和QSS3的求解效率要远低于QSS[12-14]。
为了解决QSS求解刚性问题时所出现的数值振荡现象,Migoni和Kofman[15]提出了BQSS(Backward QSS)算法,但该算法在求解非线性刚性问题时,由于误差范围较大,可能会出现“假性平衡”现象,影响仿真的推进。后续Migoni提出了一阶LIQSS(Linearly Implicit QSS)算法,它将量化变量q看作状态变量x的预测值,避免了某些扰动项对求解刚性问题所造成的影响。但是LIQSS算法要求刚性问题中的雅可比矩阵的对角线要存在较大的元素,否则可能会出现“假性振荡”现象,会对仿真求解的精度和稳定性造成较大的影响[16]。之后,Migoni等[17]又提出了改进的LIQSS算法,但在求解刚性较大的微分方程时,仍然存在求解效率较低或者无法求解的缺陷。国内学者目前研究还较少,只有文献[18-20]对QSS算法进行了初步应用。
本文将QSS算法和隐式多步法相结合,提出一种自适应多步校正算法。通过对柔性航天器动力学的仿真求解,验证了算法的可行性。从仿真精度和效率2方面,将该算法与几种典型的传统算法(ODE23tb、ODE15s、ODE45等)以及QSS算法进行了性能对比。
1 量化状态系统
常微分方程表示的状态方程系统为
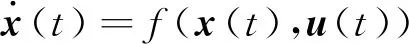
(1)
式中:x(t)∈Rn为系统的状态向量;u(t)为输入向量,QSS算法将式(1)方程重新定义为
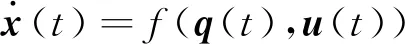
(2)
式中:q(t)为系统的量化变量,每个量化变量qi(t)均通过式(3)的迟滞量化函数得到,
(3)
式中:ΔQi为量子;qi(t-)为上一次计算的量化变量。
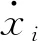
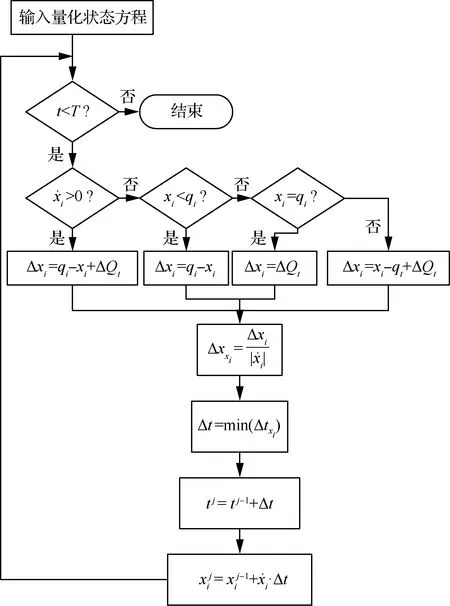
图1 QSS算法的流程图
2 自适应多步校正算法
2.1 AMCQSS
本文提出的自适应多步校正算法(Adaptive Multi-step Correction algorithm based on QSS,AMCQSS)旨在有效提高仿真精度的同时保证仿真的效率,并且拓展QSS算法求解刚性问题的应用范围。本算法以QSS算法为基础、同时结合了隐式多步法的思想:QSS算法作为显式算法,具有较好的全局误差控制特性,且其求解过程不需要迭代,保证了仿真求解的效率;多步法能够充分运用前面已经求得的多个点的信息来校正目前所需求解的值;同时本算法还可以根据计算过程中求得的导数差值来自行选择二步法或三步法,以获得更高的求解精度;此外本算法将量化变量值作为状态变量的预测值,来扼制刚性系统中可能出现的仿真数值振荡,以提高算法的稳定性和仿真求解的精度。
AMCQSS方法将式(1)近似为
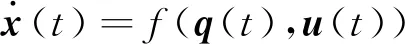
(4)
式中:q为量化变量,这里作为求x的一阶导数的预测值。
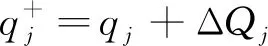
(5)
(6)
此时,状态变量仿真推进时间为
(7)
式中:k为仿真执行的步数。
当k≤2时,状态变量值的计算公式为
(8)
当k>2时,AMCQSS算法使用多步法思想对第k步的状态变量进行校正,本算法中融入了隐式多步法中的二步法和三步法思想。在求解刚性问题时,系统方程的曲线可能会在某一点突变,此时的曲线斜率会剧烈变化,该点的导数与前几点的导数相比较会产生较大的变化,这时使用二步法或三步法思想来对该点的状态变量进行校正,其校正求得的2个状态变量在数值上可能差距较大。为了保证求解的精度,将二步法与三步法求得的导数分别和第k步导数相比,选择导数值与第k步导数值相差较小的多步法。此时所选择的多步法校正后得到的第k步状态变量值是位于另一种多步法校正后得到的状态变量值和校正前的状态变量值之间,无论该点真实情况偏向于哪一边,均不会出现偏差过大的情况,这样可以有效地控制误差,避免误差积累影响到之后的仿真推进。导数差计算公式为
(9)
根据差值选择状态变量的计算公式
(10)
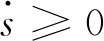
(11)
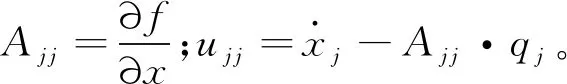
(12)
然后按式(7)~式(10)计算,最终系统每次推进的仿真时间为
Δt=min(Δtj)
(13)
2.2 AMCQSS算法的实现
算法实现(以伪代码的形式)如下:
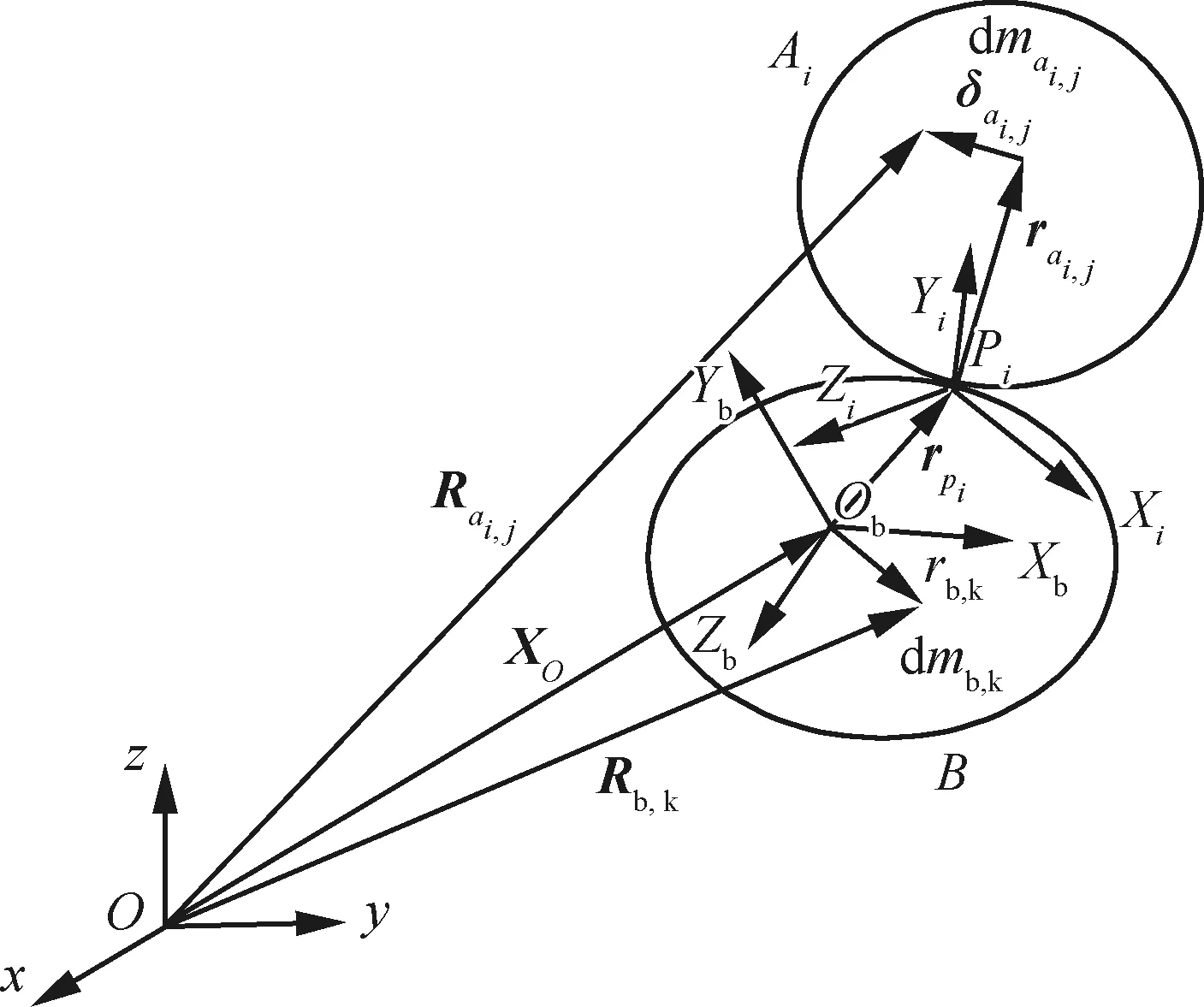
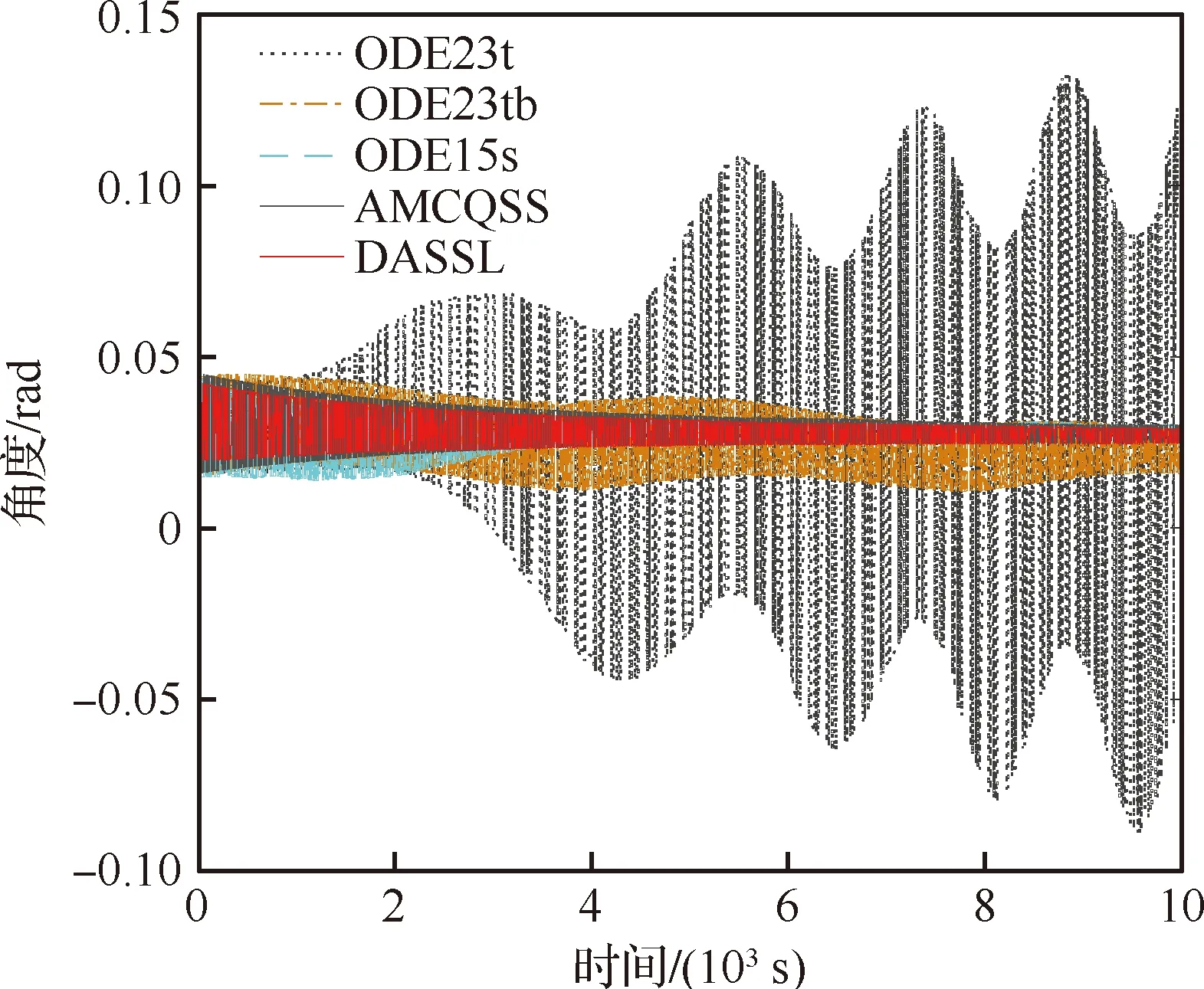
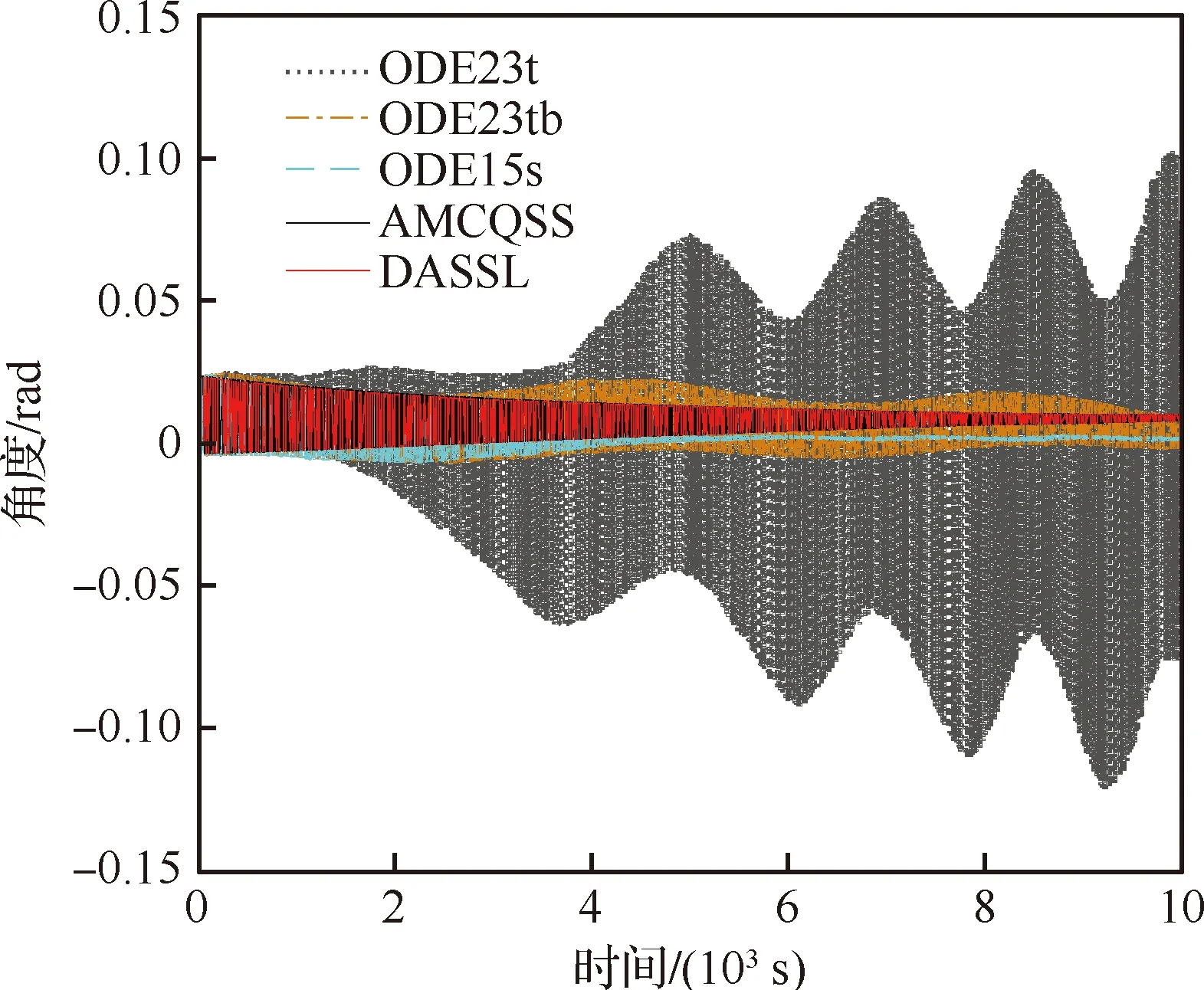
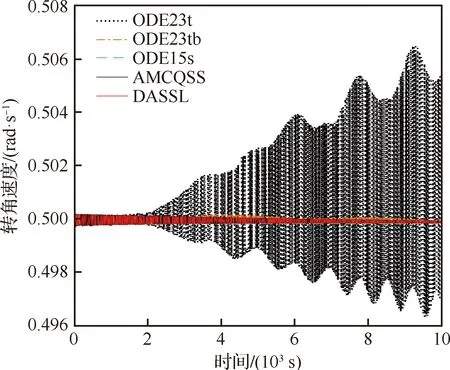
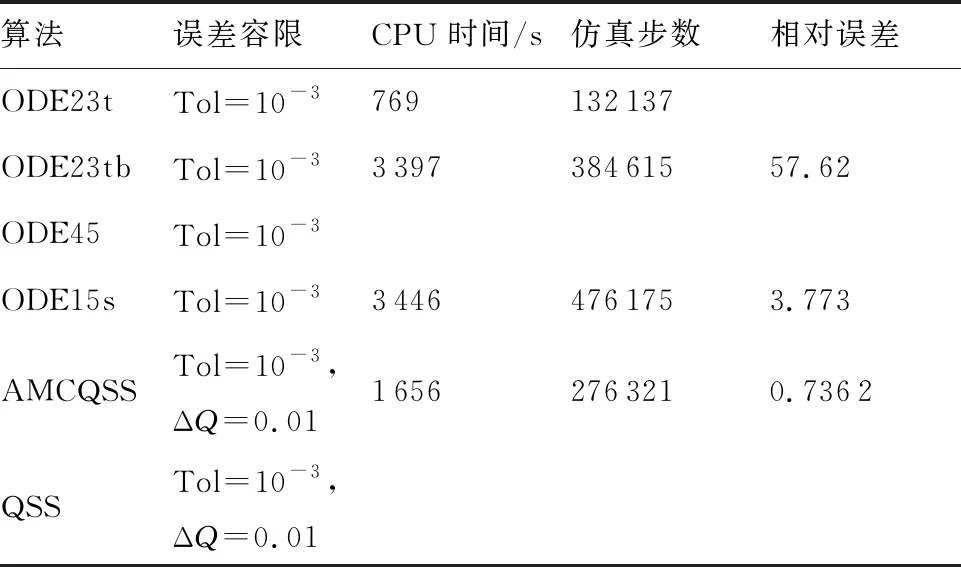
While(t for until (|xj-qj=ΔQj|) qj=xj+ΔQj qj=xj-ΔQj if (k≤2) then else else end if end if else if (k≤2)then else else end if end if end for Δt=min(Δtj) ∥(系统每推进一步,仿真的时间取状态变量的最小跃迁时间) end while 2.3.1 收敛性 (14) 假设λ(t)和λ1(t)分别为式(4)和式(14)的初始解,且λ(0)=λ1(0),则 f(λ(τ),u(τ))]dτ (15) 根据Euclidean范数,可得 (16) 设定M为函数f的Lipschitz常数,则式(16)有 MtΔx (17) 其中λ(t),λi(t)均连续,且M为正数,则根据Gronwall-Bellman不等式将式(17)改为 (18) 其中M和t不依赖于Δx,则 (19) 由式(19)可得,AMCQSS算法具有收敛性。 2.3.2 稳定性 假设式(1)是线性时不变系统,可将式(1)改写为 (20) 使用AMCQSS算法可将式(20)写成 (21) 式中:A为Hurwitz矩阵;B为系统矩阵,则AMCQSS的误差为 |e(t)|≤|V|·|Re(Λ)-1·Λ|·|V-1|·ΔQ (22) 式中:Λ为矩阵A的特征值的对角矩阵;V为矩阵A的特征向量矩阵;Re为取复数的实数部分。 由式(22)可得,AMCQSS算法的全局误差总是有界,因此AMCQSS算法具有稳定性。 图2是柔性航天器中的柔性多体卫星力学模型,将卫星本体(星体)假设为无变形的中心刚体、忽略铰连接处的摩擦力、将太阳帆板视为固连在星体上的一块均质薄板且相对星体无转动[23-26]。 图2 柔性多体卫星系统力学模型 图2中,B为星体,Ai表示为与星体连接的第i个挠性附件。引入与轨道参考坐标系等同的惯性坐标系Oxyz、星体固连坐标系Oxbybzb和挠性附件固连坐标系Pxiyizi,忽略卫星自身运动相对标称位置的小扰动[25]。Ob为星体质心;Pi为挠性附件与星体的连接点;Rb,k为点O到星体质量元dmb,k的矢径;rb,k为点Ob到质量元dmb,k的矢径;Rai,j为点O到质量元dmai,j的矢径;xO为星体质心相对于点O的小位移摄动;rpi为质心点Ob和点Pi之间的矢径;rai,j为Pi到挠性附件质量元dmai,j上的矢径;δai,j为dmai,j的振动变形矢量[25-27]。 使用模态综合—混合坐标法以及Euler-Lagrange方程对柔性多体卫星进行动力学建模,并将其转化成常微分方程形式(由于篇幅所限,本文不进行详细推导,具体过程可参考文献[25-26]): (23) 式中:ΛL和ΛR分别为左右帆板的模态刚度阵;FsaiL和FsaiR分别为整星转动时左右帆板的刚柔耦合阵;FtaiL和FtaiR分别为整星平动时左右帆板的刚柔耦合阵。为了方便计算,记FsaiL1为FsaiL矩阵的第1行,FsaiL2为FsaiL矩阵的第2行,以此类推。M为卫星质量矩阵;As为卫星的姿态变换阵(欧拉角转动顺序为2-1-3): 其中:cos表示为c;sin表示为s;α为绕惯性系y轴旋转α角,得到过渡坐标系x1y1z1;θ为绕过渡坐标系x1y1z1中x1轴旋转θ角,得到过渡坐标系x2y2z2;φ为绕过渡坐标系x2y2z2中z2轴旋转φ角,得到星体固连坐标系xbybzb,完成惯性系到星体固连坐标系的转换。 ΛR=ΛL=diag{900,14 400,16 900,250 000,280 900,360 000},左右帆板的刚柔耦合阵(单位为kg1/2·m)为 FtaiR= FtaiL= ⑤ 系统各个状态变量的相对误差计算公式为 (24) 式中:um[k]为各个算法求得的状态变量值;udassl[k]为DASSL求解器在误差设定为10-9的情况下求得的状态变量值,在此作为基准值[28]。 对柔性多体卫星动力学模型进行仿真求解,得到图3~图5所示的卫星角度及角速度变化图,其中QSS和ODE45算法无解。从图3~图5中可以看出:ODE23t出现了明显的发散,说明ODE23t不适用于该刚性问题的求解;ODE23tb虽然最终结果趋于稳定,但中间过程上下波动较大,其求解刚性问题的稳定性较差;AMCQSS和ODE15s 2种算法波动均很小,且整个过程收敛性和稳定性均较好。由表1可以看出,其中求解结果最好的传统算法是ODE15s;相比于ODE15s,AMCQSS算法在求解效率上提高了1倍多,在求解精度上提高了4倍多。 图3 卫星α角转角变化图 图4 卫星θ角转角变化图 图5 卫星φ角转角速度 表1 柔性多体卫星动力学方程的仿真结果 针对具有刚性、非线性和强耦合特点的动力学求解难题,本文提出了一种有别于传统方法的自适应多步校正算法AMCQSS,通过对柔性航天器动力学的仿真求解,得到以下结论: 1) ODE45和QSS是显式算法,在求解刚性问题时,会出现无解情况,很难满足实际工程中刚性问题的求解需要。 2) ODE23t和ODE23tb算法稳定性较差,不适于强刚性问题的求解。 3) ODE15s和AMCQSS算法稳定性和收敛性均较好,但AMCQSS算法的求解精度和效率更高,算法性能优于QSS算法和ODE15s等传统算法。
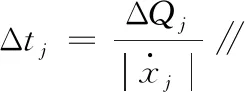
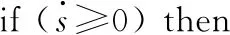
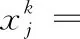
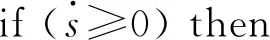
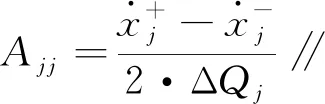
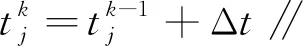
2.3 算法的收敛性与稳定性分析
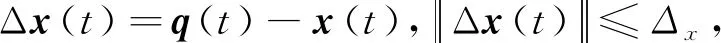
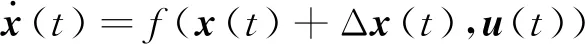
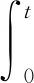
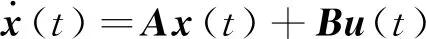
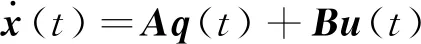
3 柔性航天器的动力学模型
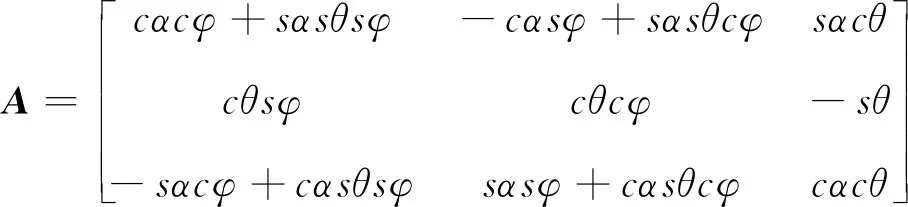
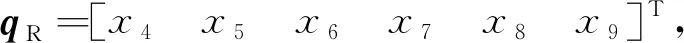
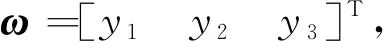
4 仿 真
4.1 仿真背景
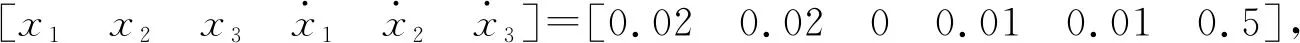



4.2 仿真结果对比分析
5 结 论
