亚声速风洞可压缩流体扰动模态分析

2021-07-07杜钰锋林俊王勋年熊能

航空学报 2021年6期

杜钰锋，林俊，王勋年，熊能

1. 中国空气动力研究与发展中心高速空气动力研究所，绵阳 621000

2. 中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳 621000

风洞试验段的核心流区域是经过导流片、蜂窝器、阻尼网等整流装置整流后风洞中流场品质最好的区域[1-4]，但尽管如此，进入风洞试验段的自由来流仍然具有非定常特性。从理论上来看，自由来流扰动是由流场中各个物理量的脉动综合导致的；而从实际的风洞结构来看，风洞运行过程中的驱动系统、加热(冷却)系统、阀门系统等均是自由来流扰动的源头[5]。自由来流扰动会对风洞试验结果的精度产生影响，致使风洞试验结果产生误差，风洞试验结果误差对于飞行器设计而言即意味着升力、阻力系数等气动参数存在设计误差，进而会导致飞行器载重量存在估算误差，严重制约了飞行器的经济性与安全性[6]。因此，对自由来流扰动进行精确量化评估就显得尤为重要。

文献[7]利用小扰动理论对流体力学基本方程进行了线性化处理，求解后发现自由来流扰动是由3种基本扰动模态叠加构成的，分别为：声模态、涡模态及熵模态，且3种扰动模态的构成成分不尽相同。声模态是由等熵状态下的压力脉动、密度脉动、温度脉动及无旋速度脉动构成的；涡模态是由有旋速度脉动构成的；熵模态是由定压状态下的熵脉动、密度脉动与温度脉动构成的[7-8]。

由于3种扰动模态的构成成分不同，其产生机制也不尽相同。一般来说，湍流边界层是声模态的主要来源，风洞中的蜂窝器与阻尼网等是涡模态的主要来源，流场中的非均匀温度场是熵模态的主要来源。文献[9]对超声速风洞中3种扰动模态的产生机制进行了溯源研究，结果表明：涡模态与熵模态在流场中沿流线传播，因此两者的产生与风洞稳定段中的流动现象有关；而声模态在流场中可跨流线传播，因此声模态的产生与风洞稳定段中的流动现象及试验段中的边界层有关。文献[10-11]利用联合模态分析方法分别对超声速风洞与高超声速风洞试验段中3种扰动模态的量值进行了测量，通过对比分析可以发现，超声速风洞与高超声速风洞试验段中声模态均为最主要的扰动模态，在超声速风洞试验段中，由于风洞没有采取加热措施，涡模态的幅值要明显高于熵模态，而在高超声速风洞试验段中，由于采取加热措施引入了熵脉动，涡模态的幅值反而要明显高于熵模态。通过对比可知，高超声速风洞中的加热装置是熵模态的重要来源。

3种扰动模态不仅产生机制不同，其对流动现象的作用机理也不相同。文献[12-13]指出，自由来流扰动中的有旋成分(涡模态)是引发边界层转捩过程中三维breakdown过程的诱因，而文献[14]指出，自由来流扰动中的无旋成分(主要是声模态)是触发二维TS波初始幅值的主要因素。不同扰动模态对边界层转捩的作用机理存在差异，在边界层转捩的预测与控制中也存在不同的作用。

综合以上分析可知：为了能够精确定量分析不同扰动模态在风洞中的源头并加以抑制，以提升风洞流场品质，提高风洞试验结果精度，并且为了能够精确定量分析不同扰动模态对流动现象的影响机理，需要对风洞试验段中的不同扰动模态均进行量化评估。目前，亚声速风洞可压缩流速域在众多客机、军用运输机、远程战略轰炸机、预警机及加油机等先进大型飞机的气动力评估及气动外形精细化设计中发挥了重要作用[15-17]，但正是由于其中的自由来流扰动模态没有进行量化评估，导致无法精确量化试验结果的精度。目前已有的研究成果绝大多数是针对超声速与高超声速风洞中自由来流扰动模态的研究[10-11,18-20]，亚声速风洞可压缩流速域的研究成果相对较少。

本文对亚声速风洞中可压缩流体在等熵条件下所包含的扰动模态进行了分析，对扰动模态求解方法及流场基本物理量声、涡模态分量求解方法进行了理论推导，建立了应用热线测速技术测量结果对其进行求解的理论关系。在马赫数Ma= 0.3～0.7进行了流场品质测量试验，利用以上理论关系对扰动模态及流场基本物理量声、涡模态分量进行了求解，对其量值变化趋势进行了分析，并利用蒙特卡洛模拟方法和不确定度传递公式对结果的不确定度进行了计算。结果表明扰动模态及流场基本物理量声、涡模态分量及其变化规律合理，且不确定度量值远小于对应变量的量值，验证了求解方法的可行性，为亚声速风洞扰动模态分析乃至流场品质评估提供了借鉴。

1 亚声速风洞扰动模态理论推导

根据文献[7]，有黏性、可压缩、可导热的气体中存在3种不同的扰动模态：声模态、涡模态、熵模态，分别服从3个准独立的偏微分方程，以下将从流体力学基本方程出发对其形式进行推导分析。对以上气体进行如下假设：① 该气体是有常比热比、常黏度系数、常热导率的理想气体；② 该气体的Pr数为0.75[21]。根据动量守恒、能量守恒、连续性方程、理想气体状态方程，气体的控制方程如下：

(1)

(2)

(3)

(4)

式中：ρ、v、p、μ、T、cp、κ、γ分别为气体密度、速度、静压、动力黏度系数、静温、定压比热容、热导率、比热比；t为时间；Φ为黏性耗散项。

对以上方程描述的气体继续引入假设：③ 根据小扰动理论，p、ρ、T、v的脉动量远小于其均值；④ 取随体坐标系对以上方程描述的气体进行分析，在随体坐标系中，介质平均速度为0。

为了便于求解式(1)～式(4)，对其中部分变量进行无量纲化处理：

(5)

(6)

将式(6)代入式(5)可知：

(7)

理想气体熵变化量方程为

(8)

式中：s为气体的比熵；R为气体常数。

对式(8)中的熵变化量进行无量纲化处理：

(9)

式中：σ为无量纲熵脉动。

利用式(7)、式(9)定义的无量纲变量及式(4)、式(8)，对部分物理量进行无量纲化，结果如下：

(10)

(11)

利用以上无量纲结果及线化处理方法对控制方程(1)～方程(3)进行处理。动量守恒方程无量纲化及线化后结果为

(12)

式中：ν为运动黏度系数，ν=μ/ρ。

对能量守恒方程进行线化处理，可得

(13)

对式(13)保留小扰动量并进行无量纲化处理，可得

(14)

由式(7)、式(10)、式(14)可得

(15)

由Pr数定义及其假设与定压比热容cp与气体常数R的关系，可得

(16)

(17)

整理式(6)、式(15)～式(17)，可得能量守恒方程无量纲化及线化后结果为

(18)

对连续性方程进行线化处理，可得

(19)

由式(11)与式(19)可得连续性方程无量纲化及线化后结果为

(20)

式(12)、式(18)、式(20)即为3种不同的扰动模态服从的引入一阶小扰动后无量纲化且线化的控制方程组。利用以上结果可推导不同扰动模态服从的独立控制方程。

对v取旋度，可得涡量ω：

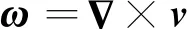
(21)

将式(21)代入式(12)中，可得

(22)

式(22)即为涡模态服从的独立控制方程，说明涡模态与声模态、熵模态无一阶干扰。

对式(12)取散度，并结合式(18)、式(20)，可得

(23)

式(23)即为声模态服从的独立控制方程，说明声模态与涡模态、熵模态无一阶干扰。

对于亚声速风洞的自由来流，可以认为是一维等熵流动[5, 22]，根据等熵关系式：

(24)

由式(11)与式(24)可知：在亚声速风洞中，无量纲熵脉动σ=0。

根据以上结果可知：在亚声速风洞中，声模态定义为式(7)，涡模态定义为式(21)，两者均服从由流体力学基本方程推导出的独立控制方程；熵模态σ=0。由涡模态的定义式(21)，常规的脉动量测量手段难以对涡量场脉动进行准确测量。根据文献[23]，可利用将平面声波导致的无旋速度脉动从总速度脉动中扣除的思想来重新定义涡模态以便于测量求解，其定义为

(25)

式中：ω为涡模态；u为亚声速风洞主流方向速度分量；Ma为马赫数；φ为平面声波传播方向与风洞主流方向的夹角。

综上所述，在亚声速风洞中，声模态P定义为式(7)，涡模态ω定义为式(25)，熵模态σ=0。

2 亚声速风洞扰动模态求解方法推导

热线测速技术由于其频响高的优点，是风洞自由来流脉动量测量最常用的手段。由文献[24]可知，利用变热线过热比方法可以对自由来流的质量流量脉动、总温脉动及其相关量进行测量，以下将利用质量流量脉动、总温脉动及其相关量作为已知量，对自由来流扰动模态及基本物理量声、涡模态分量的求解方法进行推导。

2.1 扰动模态求解方法

质量流量脉动与密度脉动和速度脉动的关系为

(26)

式中：m为质量流量。

总温脉动与静温脉动和速度脉动的关系为

(27)

式中：T0为总温。

由式(4)可得理想气体状态方程脉动量形式为

(28)

由式(24)、式(26)～式(28)可求解出压力脉动与质量流量脉动和总温脉动的关系为

(29)

由式(7)和式(29)可知，声模态与质量流量脉动和总温脉动的关系为

(30)

由式(24)、式(26)～式(28)可推导出速度脉动与质量流量脉动和总温脉动的关系为

(31)

由式(25)、式(29)、式(31)可知，涡模态与质量流量脉动和总温脉动的关系为

(32)

2.2 流场基本物理量声、涡模态分量求解方法

首先对速度脉动及总温脉动的声、涡模态分量进行求解，其关系式为

(33)

(34)

式中：下角标P代表声模态分量；下角标ω代表涡模态分量。

(35)

对于平面声波导致的声扰动模态，其压力脉动是速度脉动产生的原因。声波传播的声阻抗方程为[25]

(36)

式中：ΔuP为压力脉动导致的速度脉动。

由式(6)及式(36)可知：

(37)

将ΔuP在风洞主流方向上投影，结合式(24)与式(28)，可得

(38)

由式(35)与式(38)可知

(39)

(40)

由式(34)、式(39)、式(40)可知

(41)

联立式(33)、式(41)，可求解得速度脉动的声、涡模态分量：

(42)

对比式(32)与式(42)可知，涡模态与速度脉动的涡模态分量表达式一致，这与式(25)涡模态的定义及式(33)速度脉动的声、涡模态分量之间的关系相符。

由式(39)、式(40)、式(42)，可求解得总温脉动的声、涡模态分量：

(43)

由式(10)、式(11)可知，在亚声速风洞等熵流动前提下，密度脉动与静温脉动均只存在声模态分量，且其表达式为

(44)

(45)

根据以上推导结果可以发现：在亚声速风洞的自由来流中，由于流动可以认为是一维等熵流动，因此密度脉动与静温脉动均仅来源于声模态的贡献；而速度脉动与总温脉动来源于声模态与涡模态两者的贡献。

3 试验结果与分析

3.1 风洞试验结果

在中国空气动力研究与发展中心的探针校准风洞中利用热线测速技术对该风洞亚声速可压缩流的流场品质进行了测量，得到了部分马赫数下质量流量脉动、总温脉动及其相关量的测量结果[24]，如表1所示。表中，ρmT0为m与T0的相关系数，其定义式为

(46)

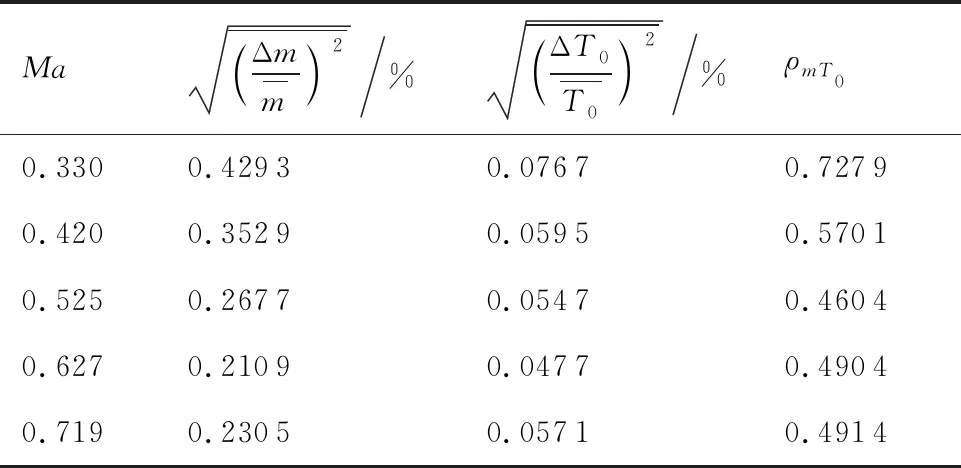
表1 流场品质测量试验结果[24]

利用以上测量试验结果，对自由来流扰动模态及流场基本物理量声、涡模态分量进行求解分析。

3.2 扰动模态求解结果

根据式(30)、式(32)中声、涡模态的表达式，可利用表1试验结果对其均方根值进行求解。对于常规亚、跨声速风洞，由于风洞试验段及其周边的收缩段、喷管、扩张段一般均为对称结构，因此试验段中的声扰动模态可视为源于向上游传播的平面声波[25]，即平面声波传播方向与风洞主流方向的夹角φ=180°。利用表1试验结果，可计算各个马赫数下声、涡模态的均方根值，结果如表2所示，其变化趋势如图1所示。

表2 扰动模态计算结果

图1 扰动模态随马赫数变化趋势

由表2及图1结果可知：随着马赫数的提高，声模态的均方根值总体上呈现出逐渐升高的趋势，而涡模态的均方根值总体上呈现出逐渐降低的趋势。

对于声模态，由于试验所在的探针校准风洞采用的是直吹射流式布局，随着试验马赫数的提高，热线探针测量点的静压逐渐降低[26]，声模态的量值总体上呈现出逐渐升高的趋势。且对于亚声速可压缩流，声模态主要源于湍流掺混噪声，但随着马赫数的提高会逐渐出现啸音和宽带激波噪声[27]，因此，在马赫数Ma=0.719的情况下，声模态的量值出现了小幅跃升。而对于低马赫数Ma=0.330的情况，由于在无引射情况下风洞马赫数直接由来流总压控制，马赫数越低即意味着总压越低，压力控制精度相对于总压的占比就越高，反映在流场上即为马赫数较低时流动参数脉动会偏大，因此，在马赫数Ma=0.330的情况下声模态量值与相邻马赫数状态相比有小幅偏高。

涡模态主要来源于有旋速度脉动，对应于风洞结构其主要产生于阀门的开闭调节、风洞的拐角段、收缩段、扩散段等使得流体速度发生改变的风洞部件，以上部件导致大尺度的旋涡产生，经过蜂窝器及阻尼网等整流装置后，大尺度的旋涡被“分割”，形成与蜂窝器、阻尼网最小结构单元尺寸相近的小尺度旋涡，最终进入试验段后，小尺度旋涡诱导的有旋速度脉动导致了涡模态的产生。对于固定的风洞结构，其在试验段中产生的有旋速度脉动量值基本上不随马赫数而改变，因此，随着马赫数的提高，涡模态量值呈现出逐渐降低的趋势。

对比声、涡模态均方根值结果可知：在马赫数较低时，自由来流中涡模态占主导，声模态由于湍流掺混噪声强度较弱而量值较低；随着马赫数进一步提高，由于湍流掺混噪声强度的提高及啸音、宽带激波噪声的出现，自由来流中声模态占主导。

3.3 流场基本物理量声、涡模态分量求解结果

根据2.2节推导结果，利用试验测量得到的质量流量脉动、总温脉动及其相关量测量结果，对各个马赫数下流场基本物理量声、涡模态分量进行求解，结果如表3所示，其变化趋势如图2所示。

表3 流场基本物理量声、涡模态分量计算结果

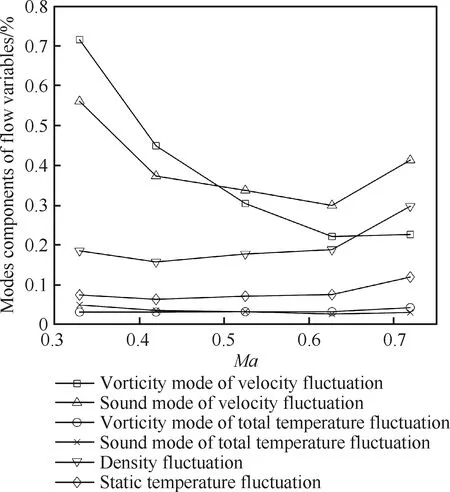
图2 流场基本物理量声、涡模态分量随马赫数变化趋势

对比速度脉动声、涡模态分量结果可知：两者量值随马赫数的变化规律与前文声、涡模态随马赫数的变化规律基本一致，即在马赫数较低时，涡模态分量占主导，随着马赫数的提高，声模态分量逐渐占主导；且在当前定义体系下，亚声速一维等熵流动中涡模态与速度脉动涡模态分量虽然定义与表达式均不相同，但两者的量值相同，这是由于忽略熵模态后其余变量构成方程组的封闭性导致的。由总温脉动声、涡模态分量结果可知：两者的量值相近且相对于其他物理量明显偏低，说明亚声速风洞中声、涡模态对总温脉动的贡献相当且均不显著，即声、涡模态均不是总温脉动的主要来源，在超声速及高超声速风洞中的熵模态才是总温脉动的主要来源。由于在亚声速风洞等熵流动中，密度脉动与静温脉动均只存在声模态分量，其随马赫数的变化趋势与声模态相同，但密度脉动量值要明显大于静温脉动，说明声模态对密度脉动的贡献要大于静温脉动，同时说明超声速及高超声速风洞中的熵模态是静温脉动的重要来源。

4 不确定度分析

为了评估流场品质测量试验结果的精度，需要对求解结果的不确定度进行评估。由于表1中的流场品质测量试验结果是通过拟合方法求解得到的，表2与表3中的变量与表1中的变量存在明确的函数关系，因此，可以采用蒙特卡洛模拟方法评估表1中的流场品质测量试验结果的不确定度[24]，再利用不确定度传递公式对表2与表3中求解结果的不确定度进行评估。

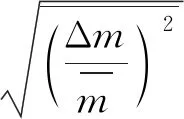
对比表1与表4中的数据可知，流场品质测量试验结果不确定度要远小于流场品质结果的量值，说明流场品质测量试验结果的精度较高。

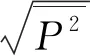
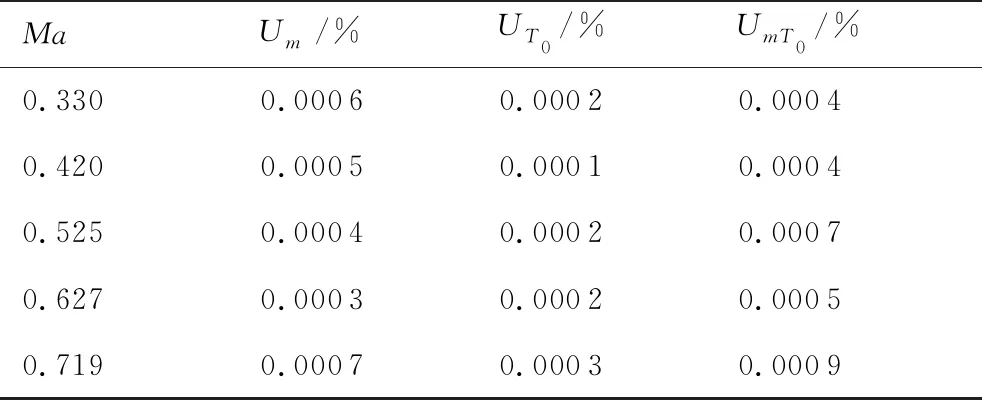
表4 流场品质测量试验结果不确定度

表5 扰动模态求解结果不确定度

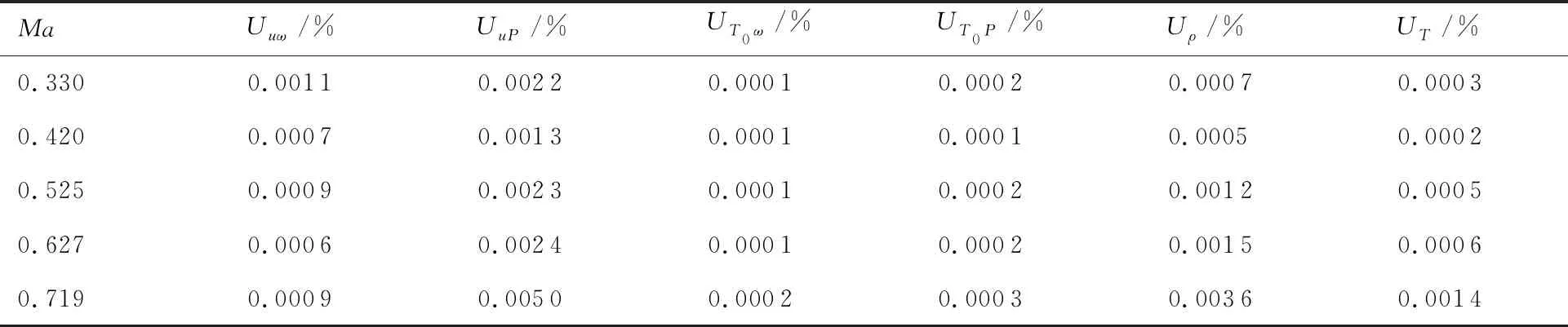
表6 流场基本物理量声、涡模态分量求解结果不确定度

对比表2与表5中的扰动模态结果及其不确定度、表3与表6中的流场基本物理量声、涡模态分量结果及其不确定度结果可知，在各个马赫数下，不确定度最高值占对应变量的1%左右，多数结果中不确定度占对应变量的比例仅为0.1%量级，不确定度的量值远小于对应变量的量值，说明流场品质测量试验中扰动模态求解结果及流场基本物理量声、涡模态分量求解结果具有较高精度。