基于量子卷积神经网络算法的微小零件识别
2021-07-06丁泽庆
何 瑞 丁泽庆
(1.黄河水利职业技术学院,河南 开封 475004;2.南阳技师学院,河南 南阳 473000)
微小零件的尺寸较小,不便于人工接触与识别。食品机械中的微小零件对产品的质量起决定作用,如饮料灌装设备中的轨迹控制轴承零件可以保证其生产线平稳,使得灌装具有一致性[1];腐竹切割刀具的零件是腐竹切割质量的关键因素[2]。
机器视觉具有效率高、非接触式识别微小零件,可全检机械零件加工生产线。神经网络(Neural Network,NN)属于监督式学习算法[3],其识别效果良好,被广泛应用于零件识别等领域,但是零件识别过程中需要较多的神经元,计算数据量大且需要较多训练样本。将小波变换与神经网络结合(WTNN)[4],需要人工提取微小零件图像特征,特征提取的效果直接影响识别精度,同时在包含多目标的零件图像中无法进行有效提取。卷积神经网络(Convolutional neural network, CNN)具有更强的提取特征能力[5],其网络结构通过局部连接实现,能够降低训练时需要的微小零件特征参数数量,由于采用误差反向传播算法进行训练,卷积神经网络存在收敛速度慢、训练成本高、泛化能力弱等缺陷。丰富功能阶段卷积神经网络算法(Rich feature hierarchies CNN,R-CNN)[6]在零件检测过程中分3个阶段:候选、提取特征信息和图像分类,各阶段相互分离,使得算法检测过程复杂,耗时较多,不便于优化。Faster R-CNN在一定程度上降低了卷积神经网络算法检测过程中的复杂度[7],但其检测速度有待提高。运用卷积神经网络的级联结构YOLOv4算法[8],其检测速度相较于R-CNN有了很大的提升,但其检测正确率较低,尤其是对于复杂场景和小目标物体的检测。
文章拟将量子算法和卷积神经网络算法(Quantum Convolution Neural Network, QCNN)结合,设计量子卷积神经网络输入层、隐藏层以及输出层量子门模型,并进行微小零件识别仿真试验,旨在为解决工业中对微小零件的快速、准确识别提供依据。
1 量子卷积神经网络算法
1.1 量子计算
量子计算单位是量子比特,其状态通过|0〉、|1〉或者叠加态构成:
|φ〉=α|0〉+β|1〉,
(1)
式中:
α、β——|0〉、|1〉状态的概率幅,且|α|2+|β|2=1。
1.2 量子卷积神经网络设计
1.2.1 量子卷积神经网络表示层模型 量子卷积神经网络由表示层、卷积层、池化层、全连接层、输出层组成,其中卷积层、池化层、全连接层可通过隐含层表示[9-10]。为了使得输出与输入能够映射相关性,通过量子受限玻尔兹曼网络,表示层模型结构如图1所示。

图1 表示层模型
表示层模型神经元经过4部分操作实现:输入由|xn〉量子比特表示、相位移动由Hadamard门与旋转门R(θl)实现、聚合由Σ操作、输出结果。多级神经网络表示层模型中,每一级表示层神经元输出结果作为下一级表示层神经元的输入,下一级依次需要经过输入、相位移动、聚合、输出4个过程,这样避免了相位移动、聚合的单一性,使得神经网络充分学习,能够增加微小零件识别的准确率。
卷积神经网络逻辑运算主要通过Hadamard门和旋转门实现,Hadamard门主要是使量子态旋转和反射,即对卷积神经网络的权值矩阵进行初始运算,其表达式为:
(2)
按式(3)计算量子门旋转:
(3)
式中:
θ——量子旋转角,rad。

(4)
则R(θ)实现了对|τ〉的相位旋转。
|xl〉经过 Hadamard门和旋转门R(θl)操作后,其结果为:
(5)
式中:
聚合结果为:
(6)
当量子位处于|1〉状态,即量子神经元的输入输出关系为:
(7)
式中:
当量子位处于|0〉状态,即量子神经元的输入输出关系为:
(8)
1.2.2 隐藏层神经元模型 隐藏层神经元量子门模型设计如图2所示。

为输入,rl为第l层的通道数,为卷积输出

1.2.3 输出层神经元模型 当对量子态进行提取时,量子态坍缩到一个具体的态上[11],为了避免卷积结果被破坏,输出层神经元线路模型设计如图3所示。

|x1〉,|x2〉,…,|xK〉为输出层的输入,|y1〉,|y2〉,…,|yK〉为输出层的分类输出结果
在输出层神经元量子门模型中,|x1〉经过Hadamard门操作后,可根据需要自由选择量子态|0〉或者|1〉进行运算,为充分进行神经网络权值更新,需要再次经Hadamard门操作后,最终输出分类结果。
1.3 参数优化
1.3.1 激活函数优化 表示层到隐含层的激活函数、隐含层到输出层的激活函数均采用修正线性激活函数ReLu如式(9)所示。
u′=min[φmax,max(φmin,u)],
(9)
式中:
φmin<0、φmax>1——激活函数ReLu边缘常量值;
u——输入;
u′——输出。
ReLu具有比动物神经元模型接收信号更准确的激活模型,如图4所示。
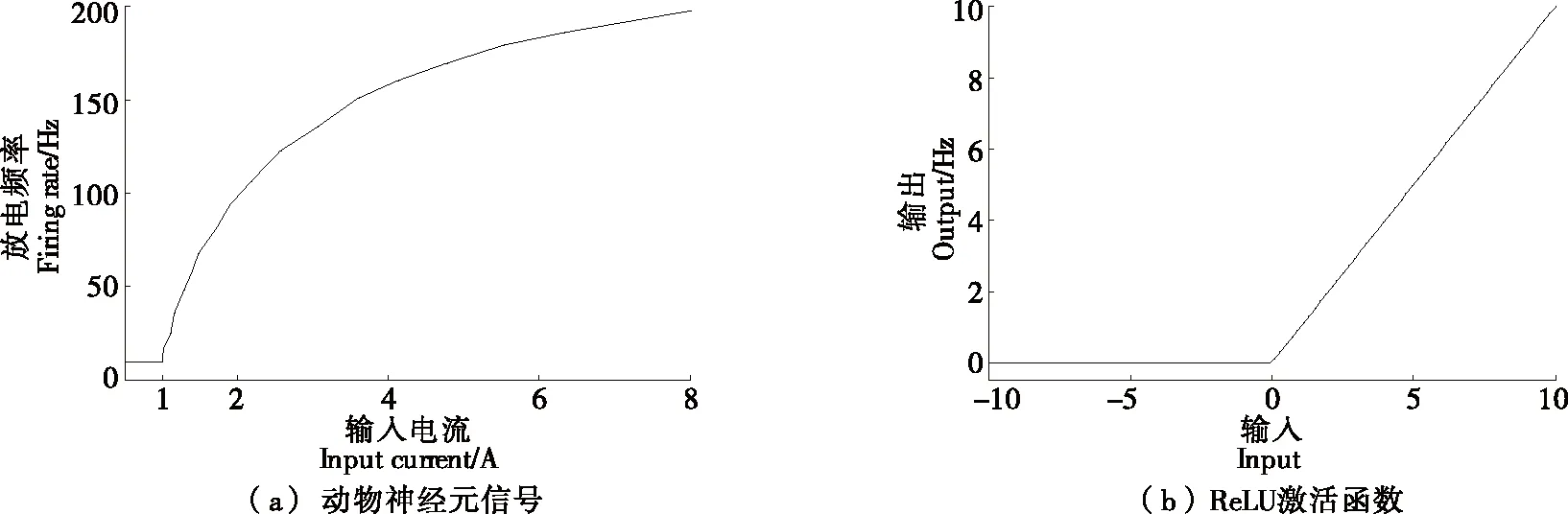
图4 激活函数示意图
与传统的Sigmoid型激活函数相比,修正线性激活函数Relu无除法和指数运算,计算速度较快,同时ReLu函数能够将负的激活值全部表示为零,使网络产生稀疏性,并且当量子卷积神经网络算法用于训练网络时,可以提升其收敛速度。
1.3.2 旋转角度、连接权值优化 神经网络算法通过量子旋转门更新时,旋转门的角度与收敛速率有关。若旋转角度值与期望值相差较大,此时需要增大旋转角度,加快收敛;若旋转角度值与期望值比较接近,此时需要减小旋转角度,以避免早熟。假设训练误差函数为:
(10)
式中:
E——训练误差值;

ym——第m个神经网络输出端的实际输出。
试验要求训练误差<10-3。
隐藏层和输出层量子旋转门的旋转角度分别为θ、ψ,其更新方式为:
(11)
式中:
t——迭代步数;
η1∈(0,1)、η2∈(0,1)——学习速率。
当训练误差较大时,旋转角度此时旋转增加,加快收敛;否则进行相反操作。
按式(12)计算连接权值。
(12)
式中:
ω——连接权值;
η3∈(0,1)——学习速率。
微小零件识别的训练器使用量子算法优化卷积神经网络的初始权值,然后生成多组固定初始权值的卷积神经网络,并对多组卷积神经网络并行计算以获得最优训练器。
2 微小零件识别过程
2.1 微小零件的特征提取
2.1.1 几何特征提取 微小零件的形状因子、球状性、矩形度、圆形度是其自身的重要特征,通常由零件所占区域的边界决定[12]。
形状因子为:
(13)
球状性为:
(14)
矩形度为:
(15)
圆形度为:
(16)
式中:
L——零件物轮廓周长,mm;




L′——与零件对象具有相同面积的面积圆的周长,mm。
当对图像进行旋转和平移时,微小零件的几何特征不发生改变。在获得零件的各个轮廓之后,几何特征为对应的轮廓内区域的形状因子、球状性、矩形度和圆形度。
2.1.2 形状特征提取 由于零件加工后在传送过程中非规则性放置,导致零件图像位置和姿态不同,但是零件的Hu不变矩具有稳定性,不因图像的旋转、缩放而改变,因此通过Hu不变矩作为零件的形状特征来识别零件[13-15]。
假设图像大小为H×S,在(p+q)阶的原点矩和中心矩分别为:
(17)
式中:
f(h,s)——图像在(h,s)处的灰度值;

归一化中心矩:
(18)
式中:
p,q=0,1,2,…;
利用二阶和三阶归一化中心矩,可以获得对平移、缩放、旋转都不敏感的7个不变矩,如式(19)所示。

(19)
但是这7个不变矩的变化范围较大,并且会出现负值,因此需要设计新的7个不变矩如式(20)所示。
Φc=|lgϑc|,
(20)
式中:
c=1,2,…,7。
根据零件图像A和零件图像B的几何特征、形状特征来识别零件A和零件B的相似度:
① 如果图像A和图像B的形状因子、球状性、矩形度和圆形度的差值均>10%,则认为图像A与图像B不相似。
② 如果图像A和图像B的形状因子、球状性、矩形度和圆形度的差值均<4%,则认为图像A与图像B高度相似,进行④。
③ 如果图像A和图像B的形状因子、球状性、矩形度和圆形度的差值为4%~10%,则认为图像A与图像B具有相似性,进行④。
④ 计算图像A和图像B的7个不变矩,如果图像A和图像B的 7个不变矩的差值均<5%,认为图像A与图像B相似,否则认为图像A与图像B不相似。
识别流程中,根据训练过程所提取的几何特征和形状特征进行比较,通过图像的相似度来判定待测零件的类别。
2.2 识别流程
量子卷积神经网络算法识别微小零件时,需要先进行量子卷积神经网络算法识别训练,当满足训练误差精度或训练次数时,即可获得零件识别最优模型,此时输入零件图像即可进行识别,其识别流程如图5所示。

图5 识别流程图
3 试验仿真
3.1 试验配置与训练结果
通过工业相机在不同时段、视角、光照场景下采集获得8种零件图像(见图6),由于零件图像有7个不变矩以及4个几何特征,因此输入层节点数为11,输出层节点数为8,隐含层节点数取10,初始化连接权值ω,旋转角度θ和ψ为[0,2π]的随机数,最大迭代步数为500,分别进行40次仿真试验。为了保证试验结果的可靠性,在数据集制作过程中,通过旋转不同角度、平移不同距离、缩放不同倍数、模拟零件堆叠、调整饱和度和曝光度等方式对数据进行扩充,并以此作为训练样本。硬件环境为CPU为Intel I7-10700KF,3.80 GHz、内存8 GB,GPU为Quadro P620,试验运行系统为Windows7.0,程序运用C++和Open CV编写,采集图像大小为640×480。

图6 8种微小零件
为了提高计算速度、减少存储空间,对图像进行JPEG格式压缩,然后灰度变换以获得连续、清晰的轮廓图像,对零件图像进行特征提取,量子卷积神经网络的期望输出结果如表1所示。

表1 零件图像特征
3.2 识别结果
训练过程中,每种零件采集70幅图像,共560幅图像进行训练。训练结束后,采用QCNN算法对8种不同的零件进行识别,每种零件采集40幅图像,共400幅图像进行识别,每种算法测试40次,不同零件的识别准确率如图7所示。
由图7可知,QCNN算法对规则的微小零件的识别准确率高于非规则的微小零件,这是因为规则的微小零件的几何特征和形状特征相对于非规则的微小零件更易于统计识别。从形态上看,零件7的外观最简单,所以最易于识别;零件8的结构特征最为复杂,所以识别准确率较低。

图7 QCNN算法对8种零件的识别准确率
增加训练样本数,每种零件采集90幅图像,共720幅图像进行训练,采用QCNN算法对8种不同的零件进行识别,每种零件采集40幅图像,共400幅图像进行识别,每种算法测试40次,不同零件的识别准确率如图8所示。
由图8可知,增加训练样本数时,各种规则、非规则的微小零件的识别准确率均有所提高,这是因为QCNN算法设计了量子卷积神经网络算法的各层模型,多次训练能够获得更加准确的卷积神经网络参数;规则的微小零件识别准确率的提高程度高于非规则的微小零件,这是因为规则的微小零件相对于非规则的微小零件更易于训练、识别。

图8 QCNN算法对8种零件的识别准确率
识别过程中每种零件的平均消耗时间如表2所示。
由表2可知,QCNN算法识别各类零件图像的耗时最少,其实时性较高,易于实现对批量零件的识别。

表2 消耗时间
4 结论
针对微小零件尺寸识别过程中存在的问题,提出了一种基于量子卷积神经网络算法的微小零件尺寸检测方法。设计了量子卷积神经网络算法的各层模型,同时优化了卷积神经网络参数,缩短了计算时间,提高了识别速度。微小零件尺寸识别中,存在识别准确率不能满足实际工作需求的缺陷,采用改进量子卷积神经网络算法能够提高识别准确率。而试验只是针对简单的微小零件进行识别,并未对复杂外观的微小零件进行识别,这将是后续研究的重点。
