互耦效应下低复杂度的二维DOA估计算法

王 凌, 潘 华, 赵 维

(海军研究院, 上海 200235)

0 引 言

空间谱估计技术区别于传统的测向技术,具有超分辨率测向能力,经过近几十年的的长足发展,在各领域取得了丰硕成果[1-6]。空间目标的二维波达方向(two-dimension direction of arrival, 2D -DOA)因能更精细地划分空间信道,具有更精确的定位目标,成为空间谱估计技术中的一个重要分支。目前已经形成以二维多重信号分类(two-dimension multiple signal classification algorithm, 2D-MUSIC)算法和二维基于旋转不变技术的信号参数估计(two-dimension estimating signal parameter via rotational invariance techniques, 2D -ESPRIT)算法为代表的二维子空间类算法理论体系[7-13]。但此类算法在阵列误差存在时估计性能明显下降,甚至失效。2D -MUSIC算法利用关系式a(α,β)UN来构造针状的二维谱峰,但当考虑互耦时,实际的方向向量已经变成Ca(α,β),此时仍然使用a(α,β)UN来进行谱峰搜索就会出现较大误差。在实际工程中,可以通过实测或预估得到互耦系数矩阵C,文献[14]证明此时用修正后的方向向量Ca(α,β)来进行二维谱峰搜索，同样也能得到正确的2D -DOA,但此时需要预先估计互耦系数,无法满足实时性要求。2D -ESPRIT算法则利用子阵列信号中子空间之间的旋转不变关系来求得2D -DOA,当互耦存在时,这种旋转不变性将被严重破坏,导致基于旋转不变技术的信号参数估计(estimating signal parameter via rotational invariance techniques, ESPRIT)算法失效。2D -ESPRIT算法无需二维谱峰搜索,计算量相较于2D -MUSIC算法大幅降低,但对于2D -ESPRIT算法来说,即使已知互耦信息,也无法构造出具有旋转不变关系的信号子空间,因此在互耦应用背景下，如何构造旋转不变性成为值得研究的课题。

另外,国内外学者针对2D -DOA估计和互耦校正作了大量的研究[15-21]。这类校正算法大致可以分为两类,一类是有源离线校正方法[15-16],该类方法需要在空间设置额外的校准源,增加了操作负担,且当校正源方位存在误差时,对校正效果影响明显。另一类是在线自校正方法[17-21],该类方法将互耦系数、DOA等未知参数转化为多参数的联合估计问题,存在多次迭代寻优、容易陷入局部最优、计算量庞大、不易工程实施等缺点。虽然可利用互耦系数矩阵的稀疏特性[20]或Toeplitz特性[21]来优化和简化迭代过程,但没有根本上解决上述问题。

针对互耦效应对旋转不变关系的破坏以及传统互耦校正算法存在的上述缺点,本文提出了一种新的完全解互耦2D -ESPRIT(mutual coupling 2D-ESPRIT, MC-2D -ESPRIT)算法,该算法通过构建互耦效应下仍保持旋转不变关系的子阵,将旋转不变技术推广至互耦应用背景。由于该算法无需二维谱峰搜索和多次迭代,且互耦抑制过程无需预知任何互耦信息,相较于传统算法,该算法计算量小,易于工程实现。仿真结果验证了该算法能抑制互耦,2D -DOA估计性能明显优于直接受互耦扰动的2D -ESPRIT算法,且接近于无互耦的标准2D -ESPRIT算法。

1 阵列信号模型及问题提出

1.1 阵列模型建立

所建立的阵列模型如图1所示，考虑空间有M个不相关的窄带信源(s1(t),s2(t),…,sM(t))分别从矢量角(θ1,θ2,…,θM)入射到由4个相互平行的均匀线阵组成的平面矩形阵列上,其中θk=(αk,βk,γk),αk,βk,γk分别为第k个信源入射方向与x轴、y轴和z轴的夹角,由于其中只有两个角度独立,故空间信源入射矢量角可表示为θk=(αk,βk),k=1,2,…,M。矩形阵列各子阵阵元间距为dx,子阵之间间距为dy。

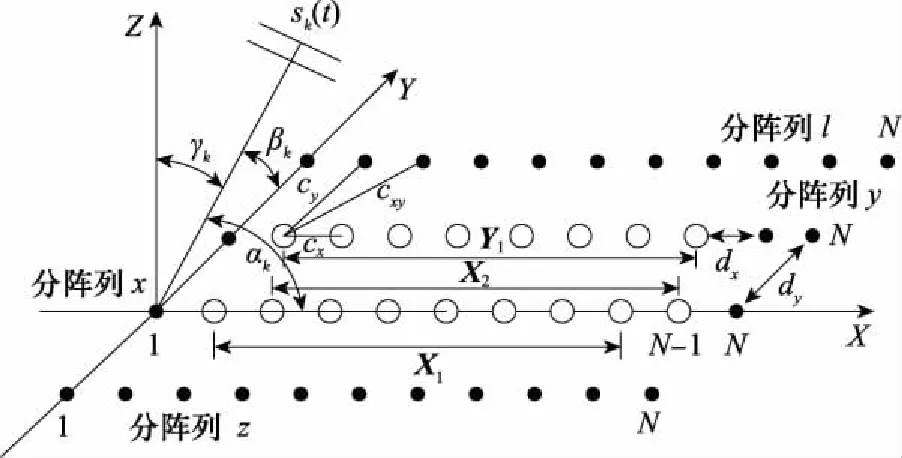
图1 阵列模型Fig.1 Array model

对于矩形阵列互耦模型的建立,本文考虑阵元周围8个阵元对其产生的互耦效应影响,同一子阵相邻阵元间互耦系数定义为cx,相邻子阵阵元间互耦系数定义为cy和cxy。此时矩形阵列互耦系数矩阵C可以表示为

(1)

式中:C1和C2为满足Toeplitz矩阵形式的N×N维子互耦系数矩阵,且

{C1=toeplitz{[1,cx,0,…,0]}

C2=toeplitz{[cy,cxy,0,…,0]}

则此时整个矩形阵列的输出可表示为

X(t)=[z1(t),…,zN(t),x1(t),…,xN(t),

y1(t),…,yN(t),l1(t),…,lN(t)]T=

CAS(t)+N(t)

(2)

式中：S(t)=[s1(t),s2(t),…,sM(t)]T为M个入射信源;N(t)为噪声矢量,其方差为σ2;A为整个阵列系统的阵列流型矩阵,可表示为

(3)

其中

A1=[a(α1),a(α2),…,a(αM)]

(4)

a(αk)=[1,u(αk),u2(αk),…,uN-1(αk)]T,k=1,2,…,M

(5)

Φ1=diag[v-1(β1),v-1(β2),…,v-1(βM)]

(6)

Φ2=diag[v(β1),v(β2),…,v(βM)]

(7)

Φ3=diag[v2(β1),v2(β2),…,v2(βM)]

(8)

(9)

(10)

1.2 问题提出

2D -ESPRIT是ESPRIT算法的二维推广形式,用2D -ESPRIT算法实现2D -DOA估计的关键是找到或构造出具有选择不变关系的子阵。经典的2D -ESPRIT算法利用图1中空心圆代表的平行阵列,构造出3个具有选择不变关系的子阵列X1、X2和Y。当不考虑互耦效应时,3个子阵信号的子空间满足:

(11)

Ψ=diag[u(α1),u(α2),…,u(αM)]

(12)

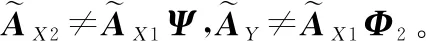
2 互耦效应下的2D -ESPRIT算法

2.1 算法实现

定义如下3个选择矩阵Q1、Q2和Q3,分别表示为

Q1=[0,J1,0,0]

(13)

Q2=[0,J2,0,0]

(14)

Q3=[0,0,J1,0]

(15)

式中:0、J1和J2为(N-3)×N维矩阵,J1、J2可表示为

(16)

(17)

在图1中将子阵x中空心圆所示阵列划分为两个子阵X1和X2,并定义子阵y中空心圆所示阵列为子阵Y,则子阵X1的接收数据可以表示为

X1(t)=[x2,x3,…,xN-2]T=Q1X(t)

(18)

将式(2)代入式(18),进一步展开,可以得到如下关系:

X1(t)=Q1X(t)=Q1CAS(t)+Q1N(t)

(19)

式中:Q1C可以写作

Q1C=[J1C2,J1C1,J1C2,0]

(20)

式中:J1C1和J1C2可表示为

(21)

(22)

注意到J1C1和J1C2最后一列全为0元素,根据矩阵理论,存在下述关系式:

Bm×(n-1)D(n-1)×p

(23)

则Q1CA表达式如下:

Q1CA=J1C2A1Φ1+J1C1A1+J1C2A1Φ2=

(24)

X2(t)=[x3,x4,…,xN-1]T=Q2X(t)=

Q2CAS(t)+Q2N(t)

(25)

式中:Q2C可以写作

Q2C=[J2C2,J2C1,J2C2,0]

(26)

式中:J2C1和J2C2形式如下:

(27)

(28)

注意到J2C1和J2C2第一列全为0元素,根据矩阵理论,存在下述关系式:

Bm×(n-1)D(n-1)×p

(29)

则Q2CA表达式如下:

Q2CA=J2C2A1Φ1+J2C1A1+J2C2A1Φ2=

(30)

式中:A12为A1的后N-1行。由于A11和A12之间存在关系式A12=A11Ψ,则式(30)进一步可写为

Q2CA=Q1CAΨ

(31)

子阵Y的接收数据可以表示为

Y(t)=[y2,y3,…,yN-2]T=Q3X(t)=

Q3CAS(t)+Q3N(t)

(32)

式中:Q3C可以写作

Q3C=[0,J1C2,J1C1,J1C2]

(33)

则Q3CA表达式如下：

Q3CA=J1C2A1+J1C1A1Φ2+J1C2A1Φ3=

(34)

由于Φ1Φ2=I,Φ2Φ2=Φ3,则式(34)进一步可写为

Q3CA=Q1CAΦ2

(35)

将3个子阵接收数据进行合并,即

(36)

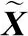
(37)

得到各子阵信号子空间之间的关系为

US2=US1T-1ΨT=US1φ1

(38)

US3=US1T-1Φ2T=US1φ2

(39)

将式(38)和式(39)求最小二乘解,可得到

(40)

(41)

对φ1和φ2特征分解即可得到旋转不变关系矩阵Ψ和Φ2,利用式(9)和式(10)对应关系,就可以得到M个入射信源分别与x轴和y轴夹角αk,βj(k,j=1,2，…,M)。式(40)和式(41)的特征分解是独立进行的,设T1和T2分别为φ1和φ2的特征向量矩阵。由于信源sk(t)与x轴夹角αk对应的特征向量和其与y轴夹角βk对应的特征向量是强相关的,因此可以利用式(42)中矩阵G每列的最大值来调整βj的顺序,从而到达匹配。矩阵G可表示为

(42)

2.2 算法步骤

本文提出的完全解互耦2D -ESPRIT算法可以总结为以下4个步骤。

步骤 1从图1所示阵列系统中提取3个子阵的接收数据X1(t)、X2(t)和Y(t)。

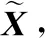
步骤 3对信号子空间US分块,并按照式(40)和式(41)求得φ1和φ2,进一步求得Ψ和Φ2。

步骤 4根据式(9)和式(10)对应关系求得αk,βj(k,j=1,2,…,M)并用式(42)来配对。

3 算法性能评估与数值仿真

前文从理论上验证了通过平面矩形阵列中对3个子阵的选取,能够抑制互耦效应对旋转不变关系的扰动,本节将对提出的完全解互耦2D -ESPRIT算法进行数值仿真验证,定量分析算法的估计性能。仿真中设定互耦系数cx=cy=0.433 1+0.251 2i,cxy=0.141 2+0.141 2i,信源DOA估计精度采用均方根误差(root mean square error, RMSE)。

仿真 13个空间不相关信源分别从波达方向(30°,90°)、(60°,60°)和(85°,75°)入射至阵列系统,设置N=10,快拍数为1 000次。设置信噪比(signal to noise ratio, SNR)为0～20 dB,试验中对比本文算法和不考虑互耦效应时的经典2D -ESPRIT算法以及受互耦影响的2D -ESPRIT算法。

估计误差随SNR变化曲线如图2所示，可以看出本文提出的算法估计性能相较于直接受互耦扰动的2D -ESPRIT算法,估计性能得到了大幅提高,当SNR高于5 dB时，估计性能和标准无互耦误差的2D -ESPRIT算法接近,仿真结果证明了本文构造的子阵能够抑制互耦对旋转不变关系的影响。从图中受互耦影响的2D -ESPRIT算法仿真曲线可以看出,互耦对子阵阵列流型的扰动显著改变了旋转不变关系,即使SNR增大,估计误差也会收敛在12°左右,因此互耦导致经典的ESPRIT算法失效。

图2 RMSE随SNR变化曲线Fig.2 RMSE curve with SNR

仿真 2固定快拍数为1 000次,改变子阵阵元数,使N分别等于10、11、12、13和15,设置SNR为0～20 dB,得到的估计误差随阵元数和SNR变化曲线如图3所示。

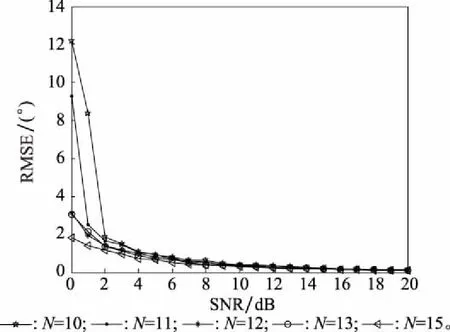
图3 RMSE随阵元数和SNR变化曲线Fig.3 RMSE curve with array number and SNR

从图3所示结果易知,本文算法在子阵阵元数小于12时,低SNR的估计性能出现较大误差,但只要SNR高于4 dB,2D -DOA的估计误差能控制在1°以内。当子阵阵元数大于12时,明显改善了低SNR时算法估计性能,图3也进一步验证了本文算法对互耦的抑制能力。

仿真 3固定阵元数为15,改变阵列系统快拍数,使快拍数分别等于700、800、1 000、1 200和1 500,设置SNR为0～20 dB,得到估计误差随SNR和快拍数变化曲线如图4所示。从结果可以看出,当快拍数高于1 000次时,算法估计误差能控制在2°以内,当SNR高于10 dB时算法估计误差已经小于0.5°。

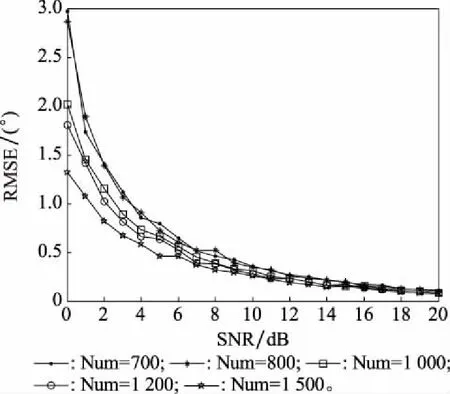
图4 RMSE随SNR变化曲线Fig.4 RMSE curve with SNR

4 结 论

传统实现互耦抑制的思路多是将互耦系数和2D -DOA作为整体进行估计,并转化为多参量非线性优化问题,在估计得到互耦参数后再利用2D -MUSIC算法进行谱峰搜索,这样无疑会导致计算量庞大等问题。而本文算法计算量仅对协方差矩阵进行一次特征分解。本文通过选取矩形阵列中3个在互耦效应影响下仍保持旋转不变关系的子阵列,无需任何互耦信息,将旋转不变思想推广至互耦扰动下的2D -DOA估计,提出了一种互耦效应下的低计算复杂度MC-2D -ESPRIT,数值仿真结果验证了该算法对互耦的抑制能力,估计精度能够接近标准无互耦误差的2D -ESPRIT算法。