可变先验贝叶斯学习稀疏SAR成像
2021-07-05沈笑云廖仙华孙卫天夏亚波
沈笑云, 廖仙华, 孙卫天, 夏亚波, 杨 磊
(1. 中国民航大学电子信息与自动化学院, 天津 300300;2. 中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300)
0 引 言
合成孔径雷达(synthetic aperture radar,SAR)作为一种军事和遥感中广泛使用的微波探测手段,具有全天时、全天候优点。在SAR成像中,经典的距离多普勒(range Doppler,RD)算法简单高效,但抑噪能力差,无法对特定目标进行特征学习成像[1]。而如何实现高分辨SAR特征成像一直是业界研究热点。近年来,压缩感知(compressed sensing, CS)[2]理论的提出,为SAR特征学习成像提供了理论和技术支持[2-3]。CS充分利用雷达成像目标数据特征,只需少量采样,就能实现原信号的无失真稀疏重建。
在CS框架下,目前常用的两种高分辨SAR特征学习成像算法分别为凸优化类算法和贝叶斯学习类算法[4]。凸优化类算法通过正则先验对特征进行建模[5]。其典型算法包括基追踪算法、稀疏梯度投影算法、快速阈值迭代算法、交替方向乘子法[6-8]等。这类算法主要优点是运算效率高。但随着成像场景复杂性和特征多样性的增加,传统单正则项已然无法满足高分辨成像要求,基于多特征的多正则项协同增强成像已成为发展趋势。然而随着正则项的增多,正则项系数地选取成为一个高维空间最优参数搜索问题,因此导致算法效率极大降低。
贝叶斯学习类成像算法则是近几年来随着统计采样技术发展起来的高分辨SAR成像算法[9-10]。该类算法采用贝叶斯统计学习框架,摒弃凸优化类算法繁琐的正则参数调整步骤,并且表现出更强大的建模灵活性与参数自学习特性。目前,贝叶斯学习成像算法主要包括变分贝叶斯-期望最大化(variational Bayes expectation maximization, VB-EM)算法、稀疏贝叶斯学习(sparse Bayesian learning,SBL)算法等[11-13]。2016年,Yang等人将贝叶斯统计学习用于SAR动目标成像,并使用VB-EM算法进行稀疏信号求解,获得较好的成像效果[14]。文献[15]基于目标散射点的连续性特征进行稀疏逆SAR(inverse SAR, ISAR)成像恢复,获得了较高精度的ISAR成像结果。但传统贝叶斯学习类算法目前主要基于目标稀疏特征或连续性结构特征进行先验建模。先验分布通常为拉普拉斯分布或高斯分布,先验建模固化,灵活性较差,难以适应复杂动态变化的目标特征,且采样求解过程面临高维矩阵求逆和随机游走采样效率低下的问题。
针对当前贝叶斯学习SAR成像算法中存在的问题,提出一种可变先验贝叶斯(variable imaging prior Bayes,VIP-Bayes)学习高分辨成像算法。该算法首先将目标特征建模为一种VIP先验,即广义高斯分布(generalized Gaussian distribution,GGD)先验[16-17]。该先验通过其形状参数的灵活可变性,可模拟适应不同的SAR目标场景成像特征,因此能很好地解决先验固化问题。其形状参数的灵活多变性赋予该先验对不同SAR目标特征进行表征的可能性[18]。然后,在先验建模基础上,进行分层贝叶斯模型,构建似然函数与GGD先验参数间的联系,进而推导成像目标后验分布。因所得后验分布十分复杂,含有lp范数指数项,无法使用常规马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)采样算法如吉布斯[19]采样进行求解。本文引入一种哈密顿蒙特卡罗(Hamiltonian Monte Carlo,HMC)采样算法[20]进行求解。HMC算法基于哈密顿动力学势能与动能守恒思想,根据梯度信息进行变量更新迭代求解,取代了传统MCMC算法的随机游走,也无需像VB-EM算法对高维矩阵求逆过程,因此计算更加便捷[21-23]。但考虑到HMC算法对非平滑成像后验分布无法求解,因此本文在HMC算法的基础上,引入近端算子[24-26],提出近端-HMC(proximal HMC,P-HMC)采样求解算法。P-HMC算法能有效解决SAR成像贝叶斯非平滑后验采样问题,因而能实现可变先验贝叶斯学习高分辨稀疏成像。
为了验证所提VIP-Bayes算法的实用性与优越性,通过仿真与实测数据实验,并与多种成像算法对比,验证了所提算法的相对优越性。并利用相变热力图方法定量分析了所提算法在不同信噪比(signal to noise ratio, SNR)和降采样率条件下的成像恢复性能。
1 SAR回波信号模型
根据SAR成像工作原理,推导出SAR成像信号模型。图1为SAR成像几何模型图。本文以机载SAR成像为研究对象,假设雷达工作于聚束模式[27],如图1所示,建立O-XYZ三维直角坐标系。
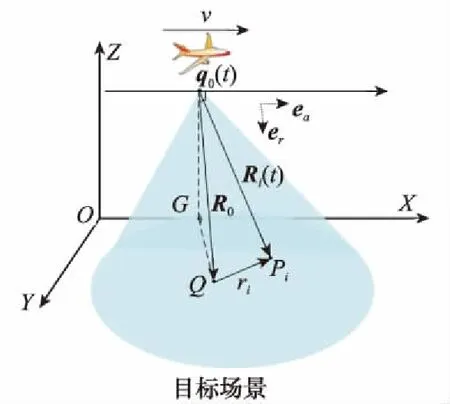
图1 SAR 成像几何模型Fig.1 Geometry model of SAR imaging
SAR载机平台以一恒定速度v沿X轴正方向(方位向)预定航线飞行并不断以正侧视方向向地面目标场景发射线性调频信号。地面场景如图1所示,Q为场景中心。G点位于雷达正下方,第i个静止目标散射点为Pi。q0(t)为参考天线相位中心。设地面目标散射点Pi到雷达天线相位中心q0(t)的斜距为Ri(t)=|R0+ri-q0(t)|,其中ri为Pi相对于场景中心Q的偏移矢量,R0为q0(t)到Q的参考斜距矢量,且R0=R0er,q0(t)=vtea,其中er、ea分别为距离向和方位向单位矢量。将Ri(t)在|R0-q0(t)|泰勒级数展开可得
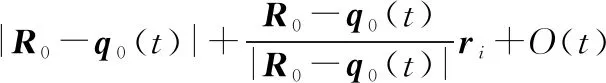
(1)
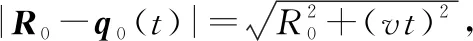
(2)
载机雷达飞过地面场景后,地面静止目标回波可表示为多散射点回波叠加形式:
S0(k,t)=
(3)
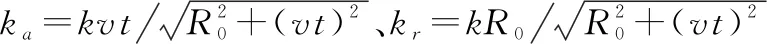
S0(k,t)=
(4)
式中:ka=-vt′/R0[14];t′表示PFA插值后方位向时间变量。经距离压缩后,可得距离压缩域数据表达式为
(5)
式中:sinc(·)为回波的距离向包络函数;λ为发射信号波长,为确定的雷达自身参数;t′为极坐标插值后的慢时间变量。
由式(5)可知,SAR回波可表示为距离向包络与方位向线性相位乘积累计求和形式。因此,SAR回波可进一步表示为以下矩阵形式的线性方程:
Y=AX+CN
(6)
式中:Y∈CK×N为观测回波;X∈CM×N为待成像的目标矩阵;M和N为方位向回波数和距离向采样点数;CN∈CK×N为杂波或噪声。在SAR模式下A∈CK×M为方位向傅里叶字典,构建如下:
(7)
式中:fd(·)为雷达运动在方位向产生的多普勒频率。通常情况下,观测回波可能为非完全数据,因此设K≤M。当K=M时,观测回波为完全数据,即Y∈CM×N,与X维度相同;当K 回波信号模型构建后,SAR高分辨成像问题可以转化为求解式(6)线性方程中变量X的问题,因式(6)通常为非齐次欠定方程,因此不能直接使用X=A-1Y进行求解。SAR回波信号Y在距离压缩域通常具有稀疏性,因此采用稀疏信号恢复方法。首先对噪声进行建模,可建模为圆对称复高斯分布,即似然函数为 (8) 传统贝叶斯学习SAR稀疏成像先验特征表征单一,先验固化,本文提出可变成像先验建模,即引入GGD先验进行先验表征。若以x为随机变量,则标准的GGD先验定义如下: (9) 图2 GGD概率密度分布Fig.2 Probability density function of GGD (10) 式中:p=[p1,p2,…,pN]、α=[α1,α2,…,αN]为不同距离向单元的形状参数和尺度参数;pn和αn分别为第n个距离向单元的形状参数和尺度参数;‖·‖pn为lpn范数。考虑到目标先验式(10)与似然分布式(8)不共轭,不能直接求解成像矩阵X的后验分布。因此引入贝叶斯分层模型进行求解。 (11) (12) 式中:I[0,2]为定义在[0,2]的指示函数,即当pn∈[0,2]时,I[0,2](pn)=1,否则为0。因而GGD先验可在[0,2]区间通过随机采样自学习获得合适的形状参数。同理,对于先验分布的尺度参数α,由于对其先验信息知之甚少,因此假设α服从Jeffreys无信息先验,分布如下: (13) 根据构建的层次贝叶斯模型,可推导获得目标成像X的联合后验概率密度函数: f(X,p,a,s2|Y)∝ (14) 根据贝叶斯分层模型,可绘制各参数或变量的有向无环图,以对各变量相互关系进行表示,如图3所示。 图3 贝叶斯分层模型有向无环图Fig.3 Directed acyclic graph of Bayesian hierarchical model 图3中,Y为观测数据,是显随机变量。X为待求解目标成像矩阵。p、α、σ2分别为GGD先验分布的形状参数、尺度参数、噪声方差,均为隐随机变量。a和b为逆伽马分布形状和尺度参数,是常量值。贝叶斯分层模型构建后,根据贝叶斯学习框架,需进一步对目标后验分布进行采样求解。 VIP-Bayes学习SAR成像算法中,目标成像建模后,后验分布采样求解为成像算法的关键步骤。统计采样技术经过近几十年的发展,目前已发展出M-H(Metropolis-Hasting)采样、Gibbs采样等经典采样算法,近年来也出现HMC等新型采样算法[21]。其中,Gibbs采样算法适合于常规统计分布采样。而M-H采样适用范围广,但效率较Gibbs采样算法低。新型HMC算法依据哈密顿动力学思想,可实现更复杂的凸分布函数采样。考虑到VIP先验下所得目标成像矩阵联合后验分布过于复杂,无法直接采样求解。因此,本文将HMC采样算法引入贝叶斯学习后验采样关键步骤中,以实现成像目标矩阵X的求解。根据式(14),首先分别推导各随机变量的边缘后验分布。 由式(8)和式(11),针对噪声方差进行边缘后验推导,可得 f(s2|Y,X,p,α)∝ (15) 式(19)为常规逆伽马分布,可直接根据该后验分布式进行Gibbs采样。对于可变GGD先验的形状参数和尺度参数,由式(10)、式(12)和式(13)可得边缘后验分布如下: f(p|Y,X,α,s2)∝ (16) (17) 式(16)中,指数项中含有lpn范数,为非常规概率分布,因此Gibbs采样算法无法进行采样求解。对于此类非常规分布,可使用M-H算法进行采样求解,使形状参数适应目标特征。针对式(17)尺度参数条件后验分布,因其为逆伽马分布,可直接根据式(17)进行Gibbs采样。 对于待求解的目标成像矩阵X,根据式(8)、式(10)进行推导,获得其边缘后验分布: f(X|Y,p,α,s2)∝ (18) 式中:指数项中涉及l2范数及lpn范数求和。对于此类复杂非常规分布,Gibbs算法无法采样求解,而M-H算法通过无方向性随机游走采样求解,效率较低。针对此问题,本文引入HMC采样贝叶斯学习算法进行求解。 HMC采样算法是一种基于哈密顿动力学思想提出的算法,2006年,Bishop将其引入统计机器学习中[21]。HMC算法以哈密顿方程为基础,基于动能和势能守恒原理提出,可实现如下分布采样: f(x)∝exp[-U(x)] (19) 式中:U(x)为势能函数,x为位移矢量。动能函数为K(q)=qTq/2σ2,q为物体动量矢量,HMC算法根据梯度信息进行蛙跳步骤[22]更新变量。 针对本文SAR高分辨成像问题中复杂分布式(24),根据HMC采样原理,势能函数为 (20) 考虑到势能函数中‖X:n‖pnpn项可能出现l1范数,使得U(X)在某些点出现不可微情况,则HMC算法无法进行求解。因此笔者在HMC采样贝叶斯学习算法基础上,引入近端算子进行梯度近似,提出P-HMC采样算法。接下来将对P-HMC算法对目标成像结果采样策略进行详细阐述。 近端方法是一种针对于非平滑函数进行的梯度近似策略[22]。设G(v)为待求解的非平滑目标函数,通常函数G(v)在x处的近端算子可表示为 (21) 式中:λ为近端尺度参数。通过近端算子的引入,HMC算法成为P-HMC算法,可解决非平滑势能函数U(X)在迭代中无法求解梯度的问题。本文SAR成像中势能函数U(X)可分解为 (22) 式中: 其中,L(X:n)为可微函数,可直接求解梯度;G(X:n)为不可微函数,需借助近端算子求解: (23) 式中:V:n为X:n的替代变量,若pn=1,即‖X:n‖pnpn表示X:n的l1范数,此时proxλ G(X:n)为复数软阈值[24]。若pn≠1且G(X:n)非平滑,可使用前后向算法进行迭代近似求解[25]。 对于平滑函数项L(X:n),求解其梯度如下: (24) 根据近端算子与梯度的关系[22],本文中SAR目标成像矩阵X中任意第n个距离向采样元素Y:n使用P-HMC算法进行变量更新,第r次迭代时更新如下: (25) (26) (27) 接受概率表示为 (28) 式中: 综上,根据超参数与目标成像结果后验计算与采样求解算法,可总结出VIP-Bayes成像算法流程。 SAR目标成像可以理解为求解成像结果矩阵X的过程。图4为VIP-Bayes高分辨SAR成像算法流程。主要包括参数与变量初始化、超参数采样求解与成像结果求解3个步骤。具体如下。首先,对各变量及参数进行初始化,设置算法总迭代次数为S,Buin-in期门限为T。Buin-in期指贝叶斯学习采样求解过程中样本收敛至目标分布前的阶段,该阶段样本不稳定,应舍去。 图4 VIP-Bayes成像算法流程图Fig.4 Solution flowchart of VIP-Bayes imaging algorithm 接着,进行3个超参数采样求解,如图4中蓝色虚线框所示。即根据式(15)对噪声方差进行Gibbs采样,根据式(16)和式(17)对可变成像先验的形状参数、尺度参数分别使用M-H算法、Gibbs采样算法进行采样求解。当3个参数更新的迭代次数大于Buin-in门限T之后,得到的样本则为可用的收敛后样本值。最后,对于成像结果矩阵X,可对距离向第n个单元成像结果Xn依次进行采样求解,最终合成目标成像结果。对成像结果矩阵X的采样求解使用前文所提的P-HMC算法,如图4中红色虚线框所示。该采样步骤中,首先进行动量变量q的初始采样,使其服从高斯分布。然后求得第r次迭代时q和X:n,并依据式(25)~式(27)进行变量更新迭代,再通过式(28)中“接受-拒绝”步骤筛选获得的目标成像结果样本。最后,通过对所得样本求期望,即可获得高分辨SAR成像结果。 为验证算法的有效性,本文首先选取仿真数据进行实验。通过与经典RD算法、SBL算法、l2范数正则约束下ADMM凸优化算法(以下简称ADMM算法)进行成像对比实验,验证了所提VIP-Bayes成像算法的优越性。最后,本文利用相变热力图分析法,定量衡量各算法在不同信噪比与降采样率下的恢复性能趋势,从而验证所提算法的优越恢复性能。 首先使用一组仿真数据进行实验,仿真参考恢复图像如图5所示,该数据由57个散射点构成,有序分布于中间十字区域内。实验中仿真实验参数如表1所示。 表1 仿真实验参数设置表 图5 仿真数据参考恢复图像Fig.5 Simulation data reference restored image 根据上述仿真参数,在仿真数据中加入噪声并进行降采样处理,分别使用RD算法、SBL算法、ADMM算法及VIP-Bayes算法进行成像恢复。实验中设置SNR=5 dB,降采样率为0.8。恢复后的结果如图6所示。其中图6(a)为RD算法恢复结果,图6(b)~图6(d)分别为SBL、ADMM算法和VIP-Bayes算法恢复的结果,对比可以看出,RD算法恢复结果中仍存在大量背景噪声。而SBL和ADMM算法恢复结果中,虽然噪声被大部分消除,但十字场景中部分散射点细节信息丢失。VIP-Bayes算法成像结果最佳,消除噪声的同时很好地保留了目标特征的完整性。 图6 仿真数据成像结果Fig.6 Imaging data results of simulation 为了定量分析仿真数据成像结果分辨率性能,根据上述仿真实验参数,选取其中单个散射点进行点目标仿真成像获得仿真结果如图7所示,其中图7(a)为单个点目标成像的三维结果图,形状为二维Sinc函数。图7(b)和图7(c)分别为距离向和方位向频谱图,均为未加窗函数抑制旁瓣结果。通过图7(a)测量获得距离向分辨率为1.1 m,方位向分辨率为0.87 m,与理论计算值接近。在分辨率分析中,峰值旁瓣比(pulse sidelobe ratio,PLSR)常用来评估成像性能。从图7(b)和图7(c)获得距离向和方位向分别为-13.23 dB和-18.22 dB。根据上述点目标分辨率分析结果,该实验充分证明了所提算法在仿真数据上的有效性。 图7 点目标成像结果Fig.7 Results of point target imaging SAR实测数据选取美国Sandias实验室的机载SAR实测数据集。实验选取成像场景为停靠的静止飞机,降采样率为0.6,即K/M=0.6,通过方位向的随机降采样后,分别使用RD、 SBL、 ADMM算法与本文所提算法进行成像对比。结果如图8所示。 对比成像结果可看出,图8(a)RD算法成像结果中噪声较多,对目标成像不够清晰。图8(b)中已经无法辨识成像目标,只能观察到极少数强散射点。图8(c)使用ADMM算法进行成像,可以看出目标整体结构特征较为完整,但噪声抑制能力不足,仍存在一定量的背景噪声。 图8 SAR实测数据成像结果Fig.8 SAR imaging results based on raw data 图8(d)为使用VIP-Bayes算法进行成像获得的结果。从图8中可以看出,结果中保留并增强了目标飞机的强散射稀疏特征,又保留了飞机整体的全局结构特征,同时噪声去除较为彻底,能很清晰地识别成像飞机地机翼,尾翼机身等各部分结构。该实验结果很好地体现了可变成像先验对复杂目标场景表征的动态灵活性与算法的有效性。 相变分析方法最早由Donoho提出,可用于评估各算法在不同参数下成像恢复性能。在SAR成像中,常用相变热力图(phase transition diagram,PTD)来衡量某一算法在不同SNR、降采样参数下的恢复概率[30-31]。本实验中,使用如图5所示的仿真数据,分别应用SBL算法, ADMM算法和 VIP-Bayes算法进行成像恢复实验,并将恢复后的成像结果与图5参考图像进行相关度计算,相关度越接近1则说明成像恢复性能最佳,即恢复概率越大。在本实验中,恢复概率从大到小分别使用colorbar中由大到小的颜色值表示。实验中设置的恢复阈值为0.85,即概率大于0.85的区域为可恢复区。相变图实验结果如图9所示,其中横坐标为降采样率,从0到1变化。纵坐标为SNR,变化范围为[-10,11]。红色部分表示算法对目标场景恢复概率接近于1,蓝色则表示恢复概率接近于0。对比3种算法相变热力图可看出,图10(a)红色面积最小,经计算可得可恢复概率为19.76%;图9(b)次之,可恢复区对应概率为22.86%;图9(c)可恢复区面积最大,可恢复概率为40.95%。因此,实验表明VIP-Bayes成像算法恢复性能优于其他两种算法。另外,在SNR较低的区域,如图9(c)所示,当SNR=-2 dB时,图中仍有一半区域为红色,说明VIP-Bayes算法在SNR较低时仍有不错的成像恢复性能。 图9 不同算法PTD结果Fig.9 PTD results of different algorithms 本文针对高分辨SAR成像中,传统贝叶斯学习成像算法先验固化问题,提出一种可变成像先验贝叶斯学习高分辨成像算法。该算法基于动态可变GGD先验对目标特征进行灵活表示,并引入P-HMC采样算法应用于复杂目标成像后验求解。本文实验部分对SAR实测数据进行成像实验,证明了所提算法相比于其他传统算法具有较好的成像恢复性能。另外,发现凸优化类算法和贝叶斯类算法具有许多共同特征,凸优化类算法正则项与贝叶斯学习算法先验分布具有一定的等价性。凸优化类算法正则项多样,而统计学习类算法已知可用统计先验较少,但无需繁琐参数调整过程。若能将凸优化类算法与高效统计采样算法结合起来,充分发挥两者优势,这将会具有很广阔的应用前景,也将是后续研究工作重点。2 SAR成像可变先验统计建模
2.1 广义高斯先验建模
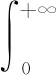
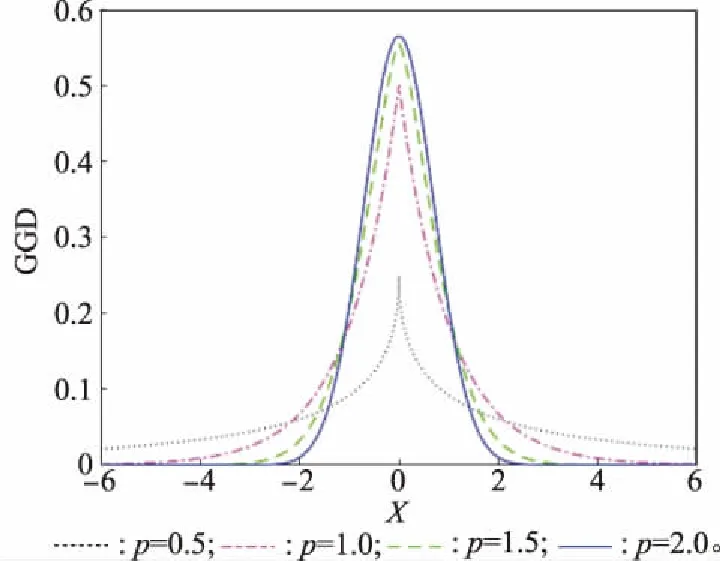
2.2 贝叶斯分层建模

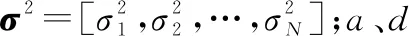
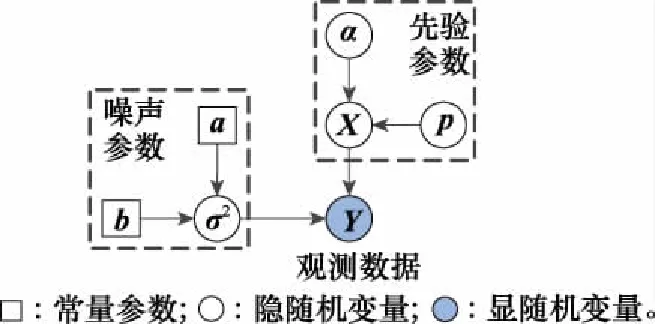
3 VIP-Bayes学习SAR成像算法
3.1 超参数后验分布计算
3.2 成像结果后验分布计算
3.3 近端-HMC采样策略

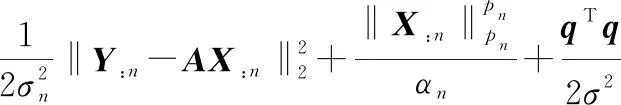
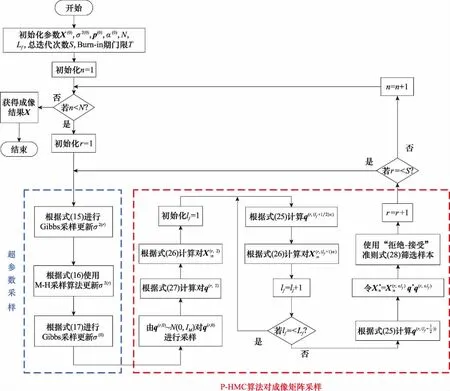
4 VIP-Bayes成像算法流程
5 实验验证
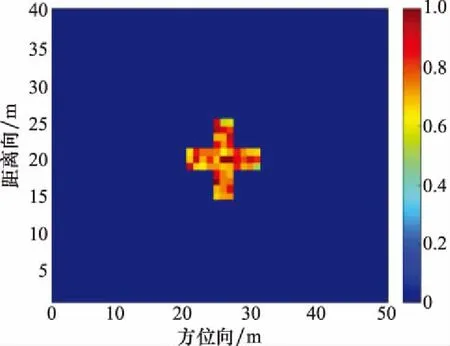
5.1 仿真数据实验

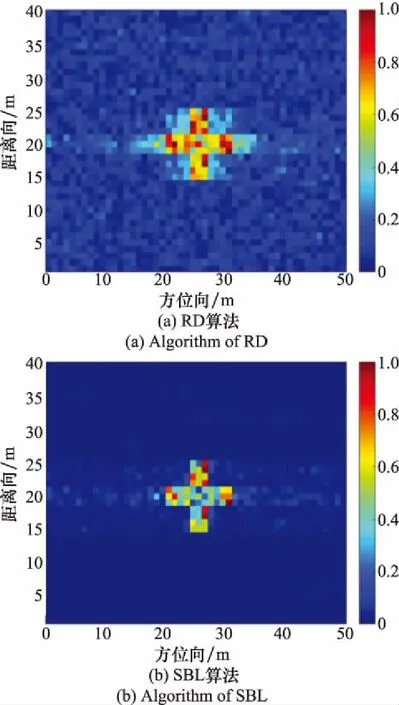
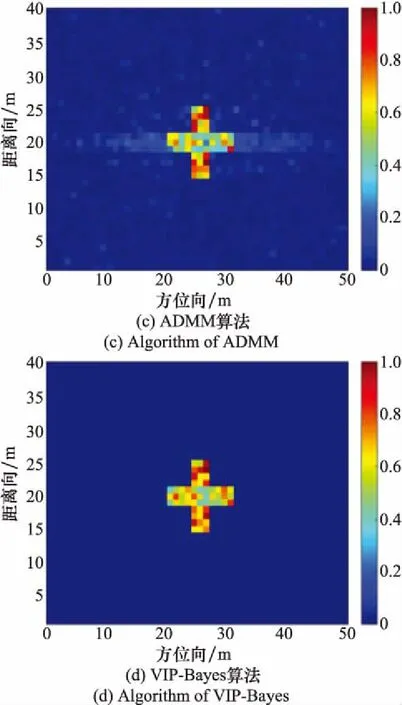
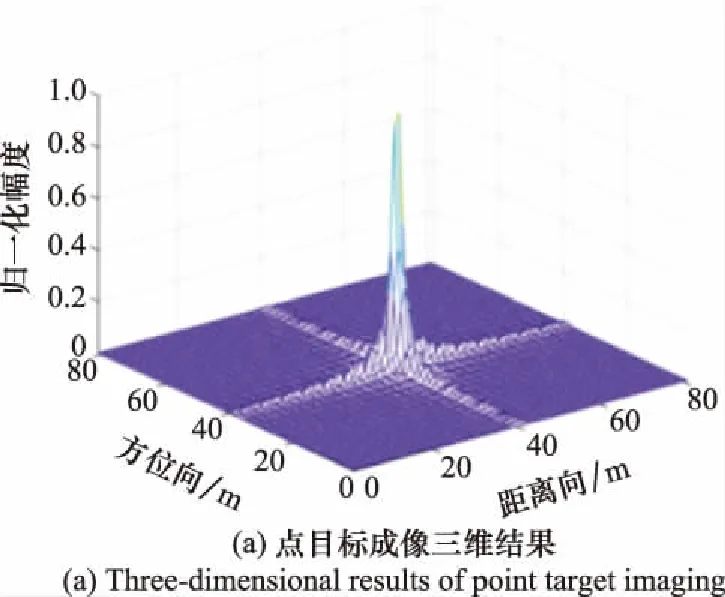
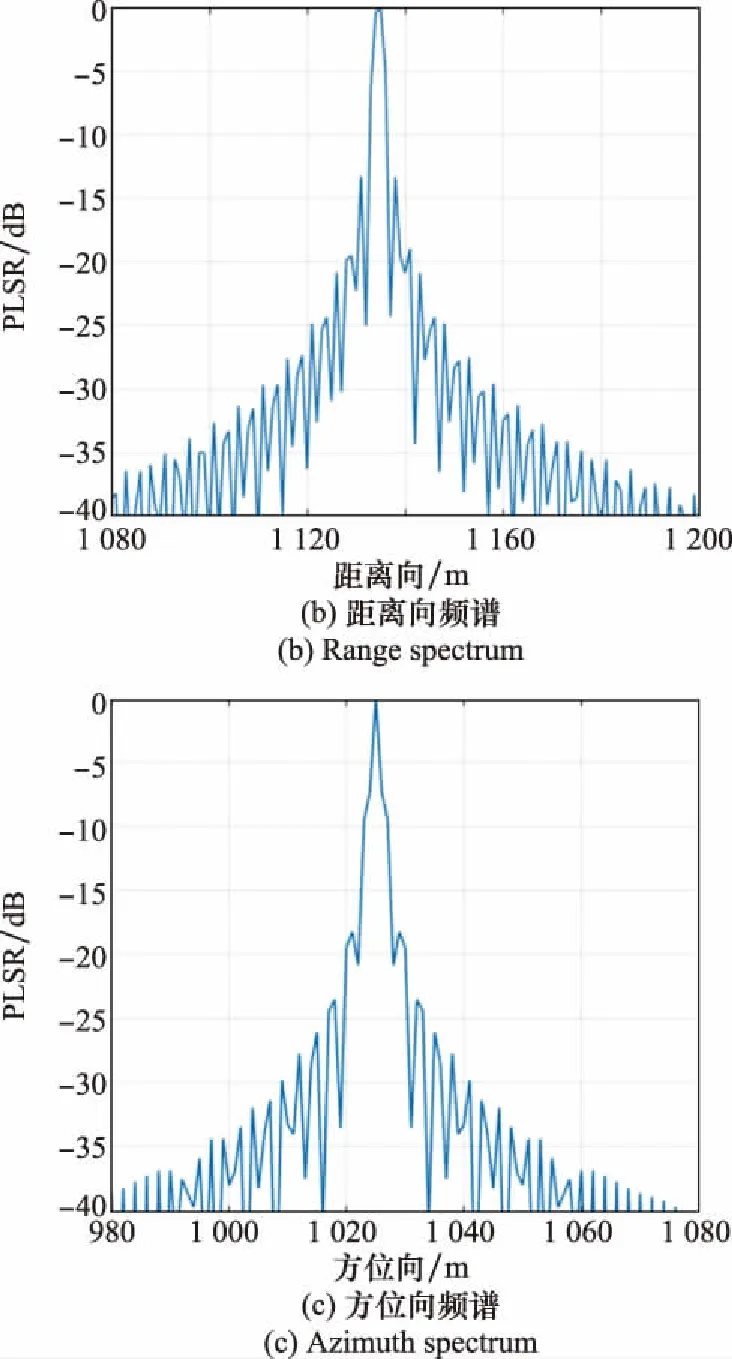
5.2 实测数据实验

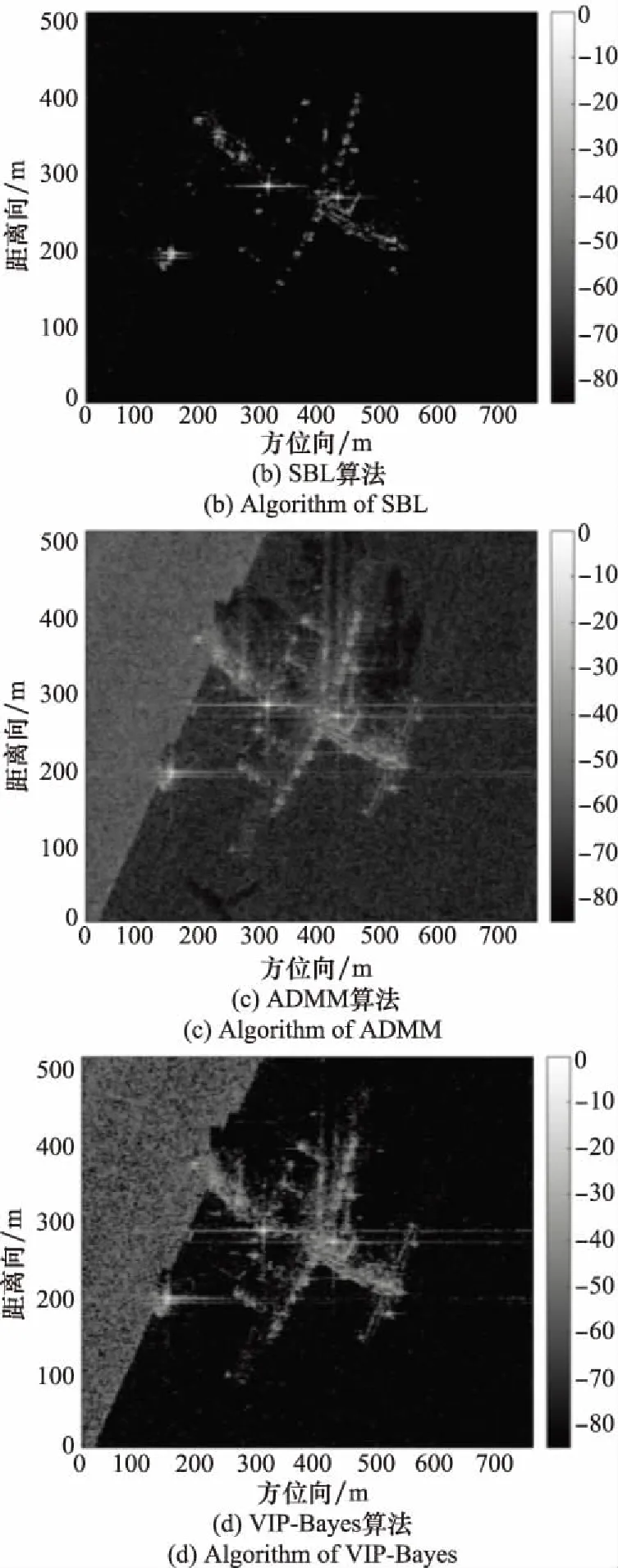
5.3 相变分析实验

6 结 论
