富水深埋隧道围岩渗透扰动高度计算方法研究

李 姝， 陈炜韬， 方 霖

(1. 四川水利职业技术学院， 四川 成都 611231； 2. 中国电建集团成都勘测设计研究院有限公司，四川 成都 610072； 3. 四川省交通勘察设计研究院有限公司， 四川 成都 610031)

0 引言

随着我国交通路网的逐渐完善，交通基础设施建设的重心逐渐向我国西南地区转移，如川藏公路、川藏铁路等[1]。我国西南地区具有地势高差大、地下水资源丰富、生态环境脆弱等地质环境特点[2]。同时，随着交通基础设施路网的完善，深埋富水山岭隧道的修建数量将会日益增多[3]。深埋富水山岭隧道在施工、运营期通常采用隧道排水系统进行排水泄压，以降低衬砌背后所受的水压力，从而保证衬砌结构的稳定。但这种排水泄压过程会对隧道周边围岩渗流场产生明显的扰动，倘若过度排水，可能会引起地表塌陷、上覆植被缺水死亡等严重危害生态环境的现象发生[3]。因此，隧道排水过程对周边围岩渗流场的扰动影响问题引起了国内外众多学者的关注。

目前，国内外针对深埋富水山岭隧道渗流场扰动问题研究，主要集中在如下方面。

1)采用控制变量法，定性分析不同因素(包括水头高度、渗透系数、排水率、注浆参数(厚度及注浆压力)等)对隧道周边渗流场分布的影响规律，探明不同影响因素下围岩渗流场的扰动变化过程，且所采用的研究方法主要以数值模拟和室内试验为主。如： 张梅等[4]分析了注浆厚度、排水率对隧道渗流场分布规律的影响； 李金城[5]、王林等[6]、杨天鸿等[7]研究了水头高度、渗透系数等因素对围岩渗流场分布的影响规律； P. A. Witherspoon等[8]分析了裂隙岩体条件下围岩渗流场的分布规律； D. T. Snow[9]探明了裂隙岩体等效渗透系数与围岩渗流影响范围的相互关系； M. Oda[10]明确了节理岩体条件下围岩渗流场演变规律，给出了节理岩体等效渗透系数的计算方法。

2)分析不同因素对隧道衬砌背后水压力的影响规律，明确不同影响因素与衬砌背后水压力的相互关系，并提出相应的水压力计算方法，且所采用的研究方法主要以理论分析、现场实测、室内试验为主。如： 王秀英等[11]分析了不同注浆层厚度对围岩渗流场的影响规律； 刘强等[12]探明了不同排水条件下隧道周边围岩渗流场分布规律； M. E. Harr[13]采用镜像法，给出了隧道围岩渗流压力的计算方法； M. Bouvard等[14]和J. O. Bickel等[15]分别基于达西定律与现场实测数据，建立了深埋隧道周边围岩渗流压力理论与经验计算方法。

从国内外研究现状总结分析可知，目前针对不同因素对隧道周边渗流场影响规律研究，多数仅分析了单因素对围岩渗流场的影响规律，而针对多因素作用下围岩渗流场扰动规律研究尚不充分。同时，针对不同因素对渗流场扰动的分析多数集中在定性分析，未见针对隧道周边渗流场扰动影响的相关定量计算方法。

本文首先采用数值模拟方法，探明隧道排水对周边围岩渗流场分布的影响规律，提出围岩渗流扰动高度概念，并将围岩渗流扰动高度作为评价隧道排水对渗流场扰动程度的评价指标；进而，采用控制变量法，分别分析水头高度、隧道排水率以及围岩渗透系数对围岩渗流扰动高度的影响规律；最后，采用数理拟合方法，给出围岩渗流扰动高度的计算方法，并采用室内模型试验对所提出的计算方法进行验证。

1 依托工程概况

本文以青藏高原地区派墨公路多雄拉隧道为工程依托，分析不同因素条件(水头高度、围岩渗透系数、隧道排水率)对隧道周边围岩渗流场扰动的影响。该公路隧道开挖直径为9.13 m，采用1台双护盾TBM单向掘进，隧道采用预制管片作为衬砌支护结构。隧道衬砌管片直径为8.1 m、宽度为1.8 m、厚度为0.35 m,其拼装方式如图1(a)所示。该公路隧道最大埋深为812 m、平均埋深为400 m以上，隧道最大水头高度为120 m，属富水深埋山岭隧道。

隧道水头较高，且地下水补给丰富。依托隧道采用泄水孔排水系统，对预制管片衬砌背后水压力进行排水泄压。每环预制管片布设2个泄水孔，分别布置在隧道左、右两侧墙角位置处，如图1(b)和图1(c)所示。隧道排水过程如下： 首先，通过每环预制管片上的泄水孔将衬砌背后地下水由泄水孔引流至隧道底部；进而，通过隧道底部排水通道直接将地下水排出隧道洞外，以实现衬砌背后水压力的泄压，同时保证隧道洞内不产生积水。

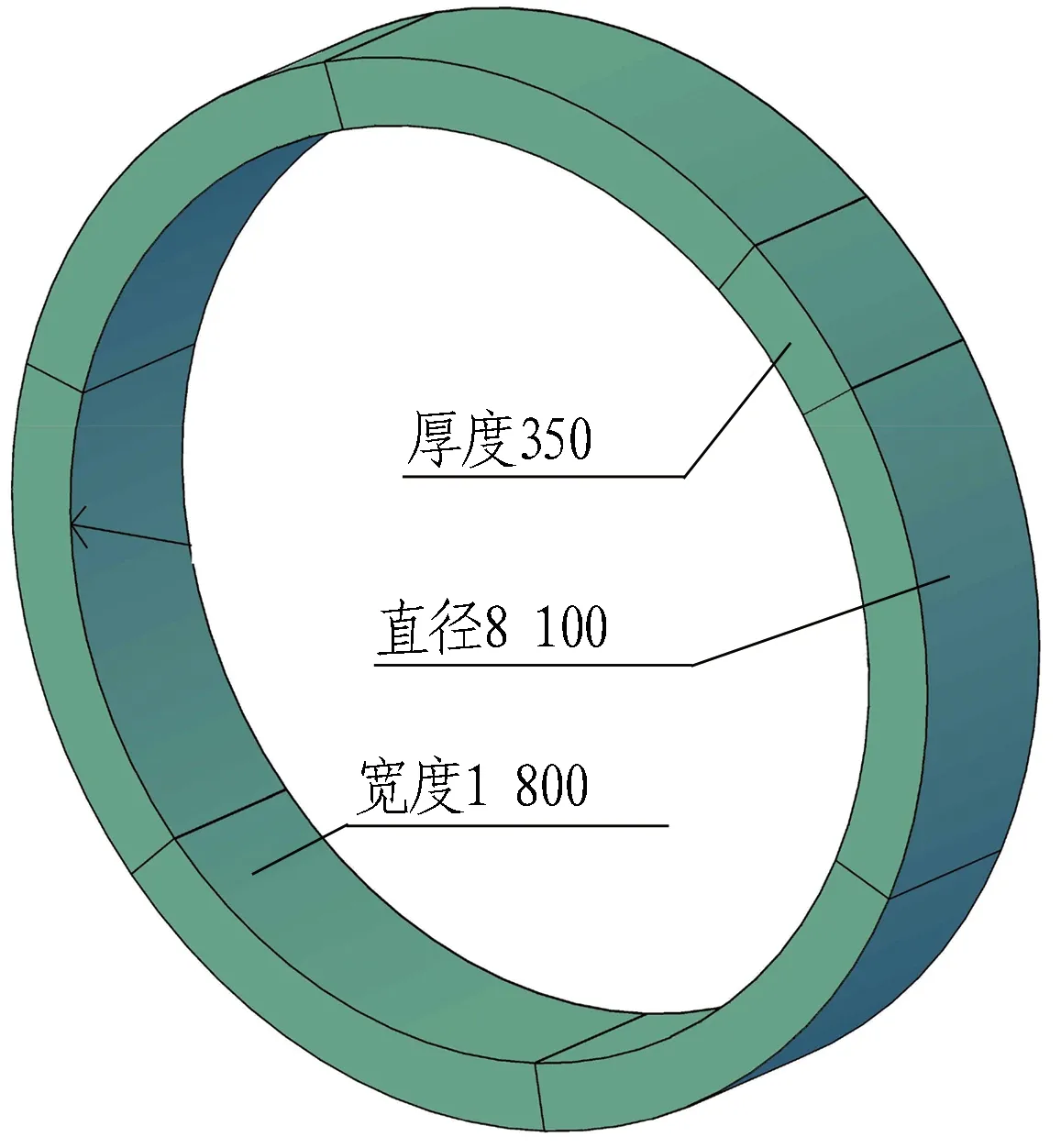
(a) 隧道衬砌管片拼装方式

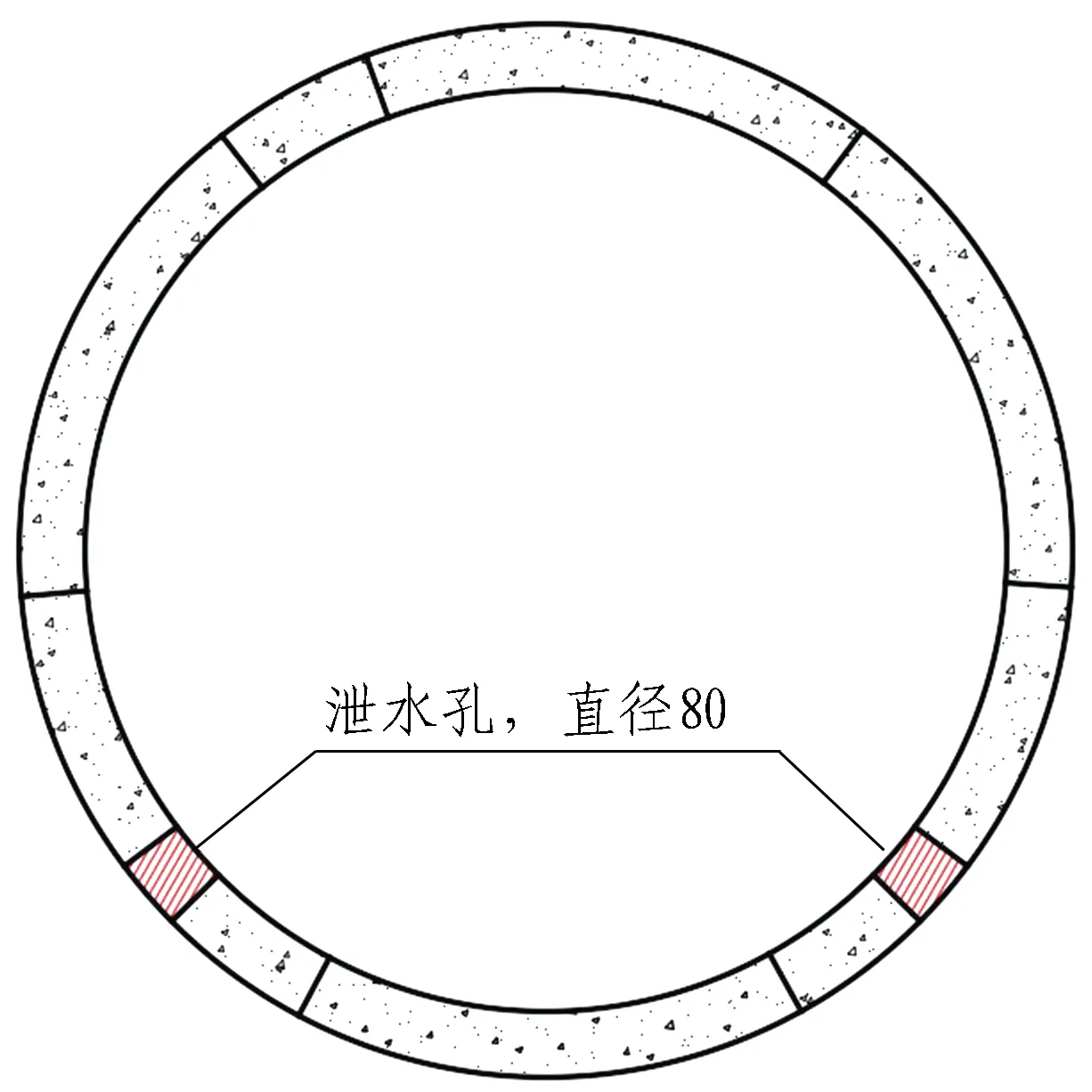
(b) 预制管片泄水孔

(c) 现场泄水孔排水过程

2 富水深埋隧道渗流场数值模拟

2.1 数值计算模型

为考虑上述不同因素对富水深埋隧道周边围岩渗流场的影响，采用Flac3D数值模拟软件中渗流场分析模块，建立围岩-隧道三维计算模型，分别分析水头高度、围岩渗透系数、隧道排水率对隧道周边围岩渗流场的影响。其中，数值模拟分析计算过程服从以下假定： 1)围岩为连续均质各向同性介质； 2)围岩渗流服从Darcy定律； 3)围岩处于饱和状态。

围岩-隧道三维计算模型如图2(a)所示。模型x轴方向长度为600 m，y轴方向长度为600 m，z轴方向长度为0.35 m，隧道顶面距模型顶面400 m，即该模型可模拟最大水头高度为400 m。数值模型边界条件如下： 模型左、右侧及顶面分别为透水边界，边界处水流可自由流动； 模型底面为不透水边界，渗透系数为0。隧道衬砌结构，根据图1中管片结构尺寸进行构建，如图2(b)所示。围岩-隧道三维数值模型中围岩、衬砌管片均采用实体单元模型，渗流本构模型为各项同性渗流模型，数值模拟模型单元总数为40 876个，节点总数为225 256个。围岩和衬砌单元均为实体单元，本构模型为各向同性渗流本构模型，孔隙率为0.3%，体积模量为2 GPa，流体抗拉强度为0。

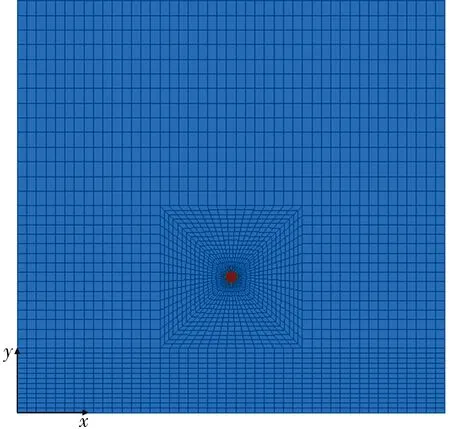
(a) 围岩-隧道三维模型

(b) 管片衬砌三维模型

2.2 数值模拟监测点布置

为方便监测不同因素对隧道周边渗流场的影响，在数值模型中设置渗流压力测线，其测线布置方式以隧道中心为原点，每间隔15°布设1条放射状测线，且每条测线中以10 cm间隔布置测点。围岩渗流压力监测点布置如图3所示。

2.3 数值模拟计算工况

采用控制变量法，分别分析水头高度、渗透系数、排水率3个因素条件下周边围岩渗流场分布规律。以渗透系数作为数值模拟主要工况划分指标，制定5组主要工况；其中，每组主要工况中又根据水头高度、排水率制定84组细分工况，故数值模拟工况数目总计420组。数值模拟工况如表1所示。

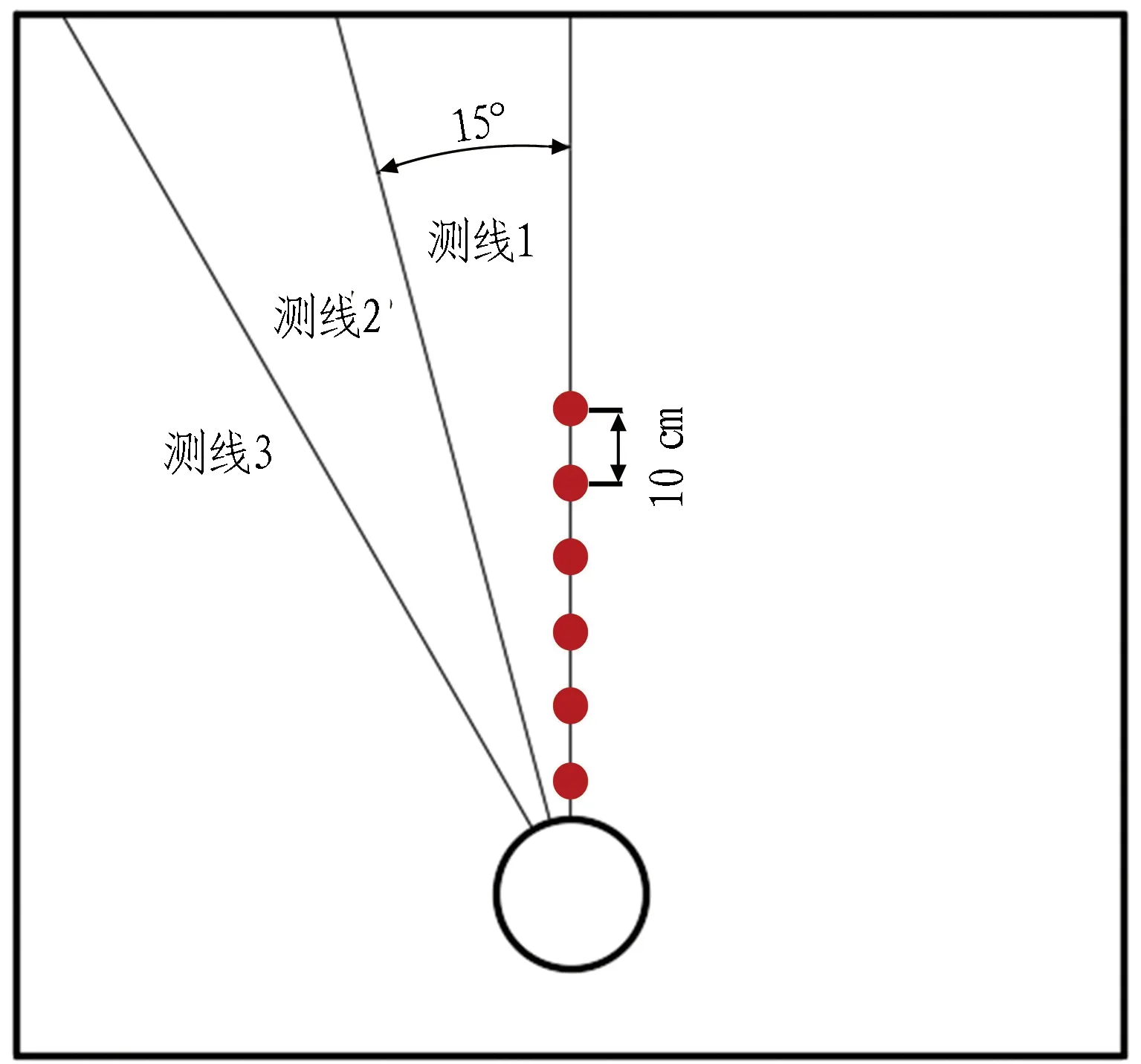
图3 数值模型监测点布置图

表1 数值模拟工况

隧道不同排水率工况模拟实现方式如下： 首先将隧道衬砌结构设为透水材料，通过调整衬砌结构的渗透系数，使其衬砌结构具有不同程度的排水能力； 进而，对衬砌结构渗透系数进行试算，同时获取试算渗透系数条件下经由衬砌结构排出的水量，并结合隧道涌水量计算得出衬砌结构试算渗透系数条件下隧道排水率； 最后，根据排水率细分工况，不断调整衬砌结构渗透系数，直至获得满足各排水率工况要求的衬砌结构渗透系数，以此实现不同排水率细分工况的模拟。

2.4 数值模拟计算流程

1)建立围岩-隧道三维数值模型，设置渗流场边界条件与围岩、衬砌实体参数，进行水头高度条件下围岩渗流场初始平衡计算，得到隧道开挖前围岩初始静水压力渗流场。

2)进行隧道毛洞开挖模拟，采用FISH语言获得隧道涌水量。

3)进行隧道衬砌支护，同时将其渗流本构模型设置为透水材料；并根据排水率细分工况要求，设置衬砌结构渗透系数，进行不同排水率工况下围岩渗流场计算，直至计算收敛。

4)通过设置的数值模拟测线，获得该工况下隧道周边围岩渗流场分布规律。

3 围岩渗流扰动高度及影响因素分析

3.1 围岩渗流扰动高度概念

以水头高度90 m、渗透系数1×10-2cm/s为例，分别给出隧道排水率为0(即不排水)与排水率为100%时隧道周边围岩渗流场的分布规律，如图4所示。

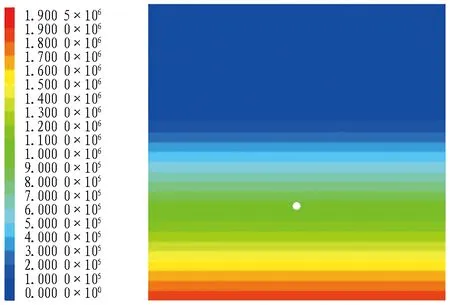
(a) 排水率为0时围岩渗流场(单位： Pa)

(b) 排水率为100%时围岩渗流场

由图4(a)可知： 当隧道排水率为0时，此时围岩渗流压力线呈水平分布，同一水头高度处各点渗流压力相等，围岩整体渗流压力分布为静水压力分布状态，并且衬砌背后水压力量值近似等于静水压力值，说明隧道不进行排水时不会对围岩渗流场产生扰动，不影响围岩渗流场初始分布状态，这点与目前大多学者研究结论一致[3,6,12,15]。

由图4(b)可知： 1)当隧道排水后，隧道周边渗流场发生明显扰动现象，隧道周边渗流场由原本的静水压力状态转变为动水压力状态，其中最为显著的变化为隧道拱顶上部位置的围岩渗流压力线分布形态由水平线转变为“漏斗”形态的曲线，隧道拱顶位置上方围岩渗流压力明显降低； 2)对比排水与不排水条件下隧道拱顶上方围岩渗流场分布规律可知，由隧道排水所引起的围岩渗流场扰动范围并不会扩散至整个围岩范围，而仅在隧道拱顶上部一定范围内存在。

为了准确评价隧道排水过程对围岩渗流场扰动的影响，本文提出围岩渗流扰动高度概念，即为在隧道埋深方向上(y轴)隧道排水前后围岩渗流压力不发生变化位置(A点)与隧道拱顶位置(B)处的最小距离。根据围岩渗流扰动高度定义，图4(b)中隧道排水率为100%条件下，围岩渗流影响高度为76.5 m。

3.2 不同影响因素下围岩渗流扰动高度

围岩渗流扰动高度受到渗透系数、水头高度以及隧道排水率的综合影响。采用控制变量法，分别分析上述3个因素对围岩渗流扰动高度的影响规律。

3.2.1 不同渗透系数条件下围岩渗流扰动高度

不同渗透系数条件下围岩渗流扰动高度如图5所示。可以看出： 给定水头高度与隧道排水率时，随着围岩渗透系数的增加，围岩渗流扰动高度呈逐渐增加趋势，两者呈正相关关系。

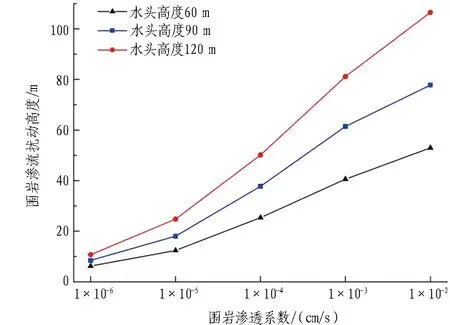
图5 不同渗透系数条件下围岩渗流扰动高度

以水头高度120 m为例，当围岩渗透系数为1×10-6cm/s时，此时围岩渗流扰动高度为10.7 m； 而当围岩渗透系数增大至1×10-2cm/s时，围岩渗流扰动高度增大至106.47 m，增大了895. 05%。

3.2.2 不同隧道排水率条件下围岩渗流扰动高度

以水头高度90 m为例，不同隧道排水率条件下围岩渗流扰动高度如图6所示。可以看出： 给定水头高度与围岩渗透系数时，随着隧道排水率的增加，围岩渗流扰动高度呈逐渐增加趋势，两者亦呈正相关关系。

以渗透系数1×10-2cm/s为例，当隧道排水率为20%时，此时围岩渗流扰动高度为67.54 m； 当排水率增大至100%，围岩渗流扰动高度增大至77.48 m，增大了14.7%。

3.2.3 不同水头高度条件下围岩渗流扰动高度

围岩渗流扰动高度随水头高度变化曲线如图7所示。可以看出： 围岩渗流扰动高度随水头高度变化曲线呈现出明显的2段式特征。1)当水头高度小于某一水头高度时(图中A′B′段)，随水头高度的增加，围岩渗流扰动高度呈现出较为明显的线性增大趋势。以排水率100%工况为例，当水头高度为60 m时，围岩渗流扰动高度为55.46 m； 当水头高度增大至120 m时，此时围岩渗流扰动高度为109.24 m，增大了96.97%。2)当水头高度大于某一水头高度时(图中B′C′段)，此时围岩渗流扰动高度表现为定值，不再随水头高度的增加而继续增加。

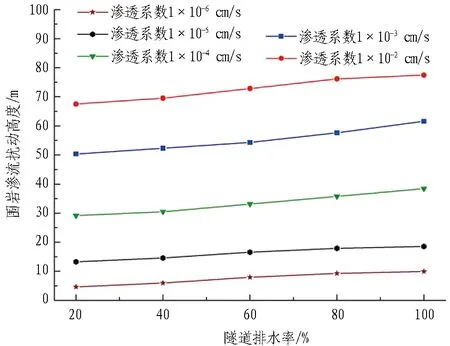
图6 不同隧道排水率条件下围岩渗流扰动高度

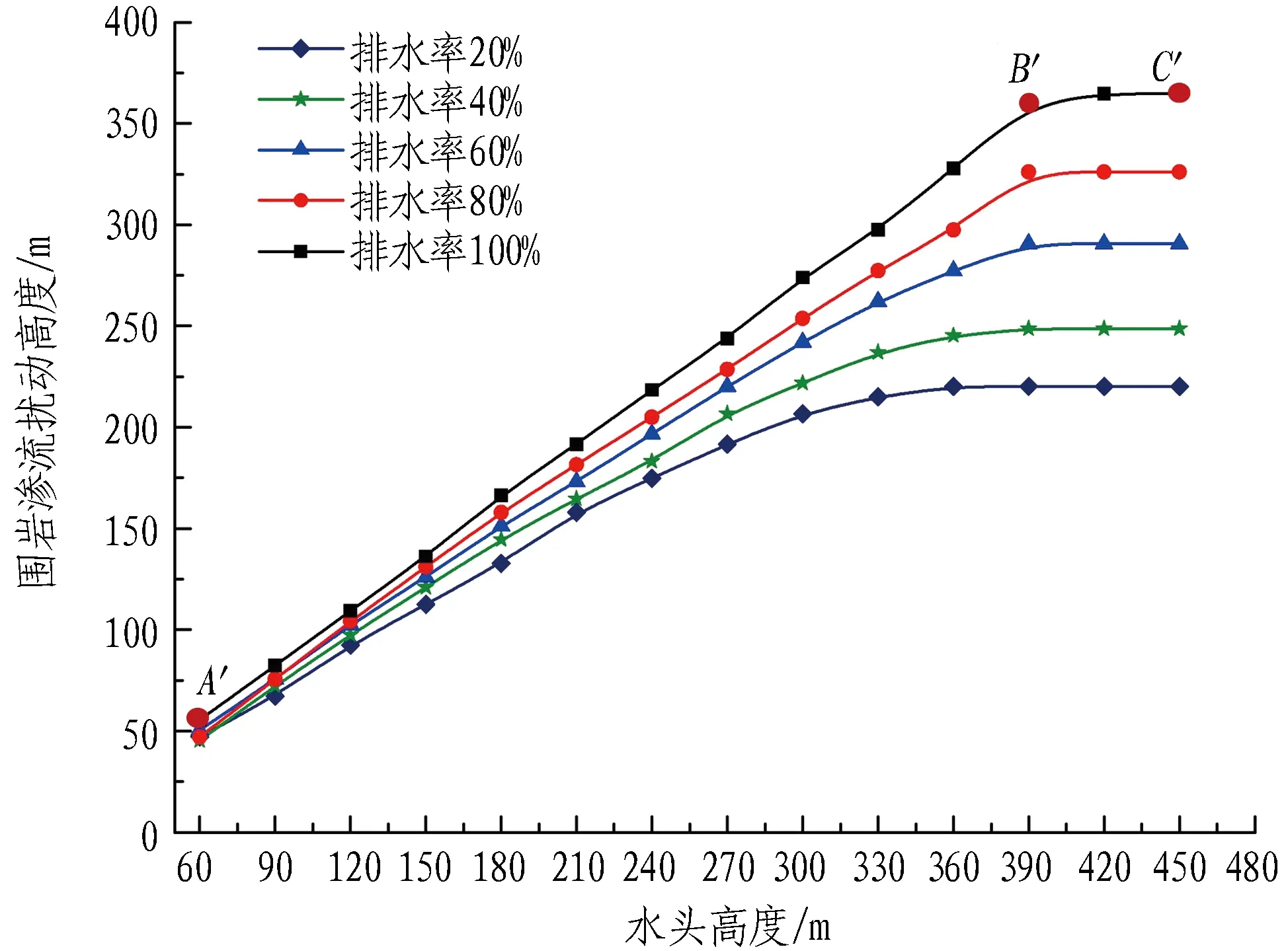
图7 围岩渗流扰动高度随水头高度变化曲线

为了更好地描述围岩渗流扰动高度随水头高度的变化规律，将B′点对应的水头高度定义为临界水头高度，对应的围岩渗流扰动高度定义为临界围岩渗流扰动高度。同时，对比水头高度、渗透系数、隧道排水率3个影响因素，其中对围岩渗流扰动高度影响程度最大的为渗透系数因素；而排水率虽然是围岩渗流扰动高度产生的根本因素，但其自身对围岩渗流扰动高度影响最小。因此，可得渗透系数、水头高度、隧道排水率对围岩渗流扰动高度影响程度依次降低。

4 围岩渗流扰动高度计算方法

由上文分析可知，围岩渗流扰动高度受到3个因素的综合影响，所以给出的计算方法中应能体现上述3个影响因素。首先根据上述水头高度与围岩渗流扰动高度的相互关系，给出围岩渗流扰动高度随水头高度变化模型及数学表达式如下：

当H>H临界时，h=h临界；

(1)

当H≤H临界时，h=aH。

(2)

式(1)—(2)中:H为水头高度；H临界为临界水头高度；h为围岩渗流扰动高度；h临界为临界围岩扰动高度；a为待定系数。

若采用式(1)和式(2)对围岩渗流扰动高度进行计算，还需给出临界水头高度、临界围岩扰动高度与待定系数的计算方法。

4.1 H>H临界时围岩渗流扰动高度计算方法

由式(1)分析可知，当水头高度大于临界水头高度时，此时围岩扰动高度为定值。下文分别给出临界水头高度与临界围岩渗流扰动高度计算方法。

由图5可知，临界水头高度受到渗透系数与排水率的综合影响。本文采用数理拟合方法，基于数值模拟计算结果(见表2)，拟合给出临界水头高度计算表达式，如式(3)所示；拟合结果云图如图8所示。

表2 不同工况下临界水头高度

由图8可知，临界水头高度与排水率、渗透系数呈二次曲面关系，且拟合相关系数为98.3%，拟合结果良好。因此，可采用式(3)对临界水头高度进行计算。

H临界=544.8+0.76β+45.63lnk+4.64βlnk×

10-2+0.87(lnk)2。

(3)

式中：β为排水率，%；k为渗透系数，cm/s。

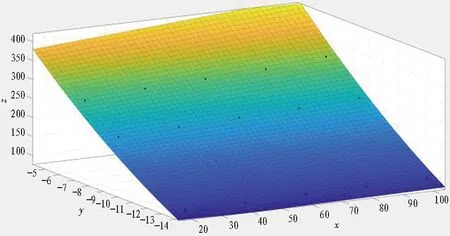
图8 临界水头高度与排水率、渗透系数拟合云图

将临界水头高度、围岩渗透系数、隧道排水率作为自变量，临界围岩渗透扰动高度作为因变量，拟合得出临界围岩渗流扰动高度计算表达式。同时，由于临界水头高度计算表达式中因变量为渗透系数与排水率。因此，临界围岩渗流扰动高度计算表达式中因变量只有围岩渗透系数与排水率。下文以渗透系数与排水率作为因变量，对临界围岩渗流扰动高度计算表达式进行拟合。不同工况下临界围岩渗流扰动高度如表3所示。

表3 不同工况下临界围岩渗流扰动高度

临界围岩渗流扰动高度与排水率、渗透系数拟合云图如图9所示。可以看出： 临界围岩渗流扰动高度与排水率、渗透系数呈二次曲面关系，且拟合相关系数为99.42%，拟合结果良好。因此，可采用式(4)对临界围岩渗流扰动高度进行计算。

h临界=459.3+2.78β+74.45lnk+0.21βlnk+

3.05(lnk)2。

(4)

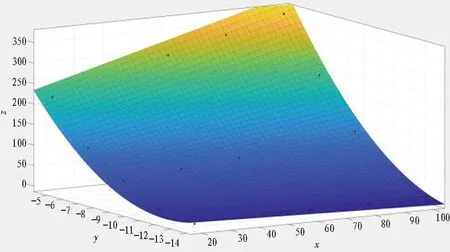
图9 临界围岩渗流扰动高度与排水率、渗透系数拟合云图

4.2 H≤H临界时围岩渗流扰动高度计算方法

由式(2)可知，当水头高度小于等于临界水头高度时，围岩渗流扰动高度随着水头高度的增加呈线性增加趋势； 且两者比例系数仅与围岩渗透系数与排水率有关，而与水头高度无关。因此，采用数理拟合方式，以渗透系数与排水率作为因变量；比例系数作为自变量进行数理拟合。不同工况下比例系数如表4所示。

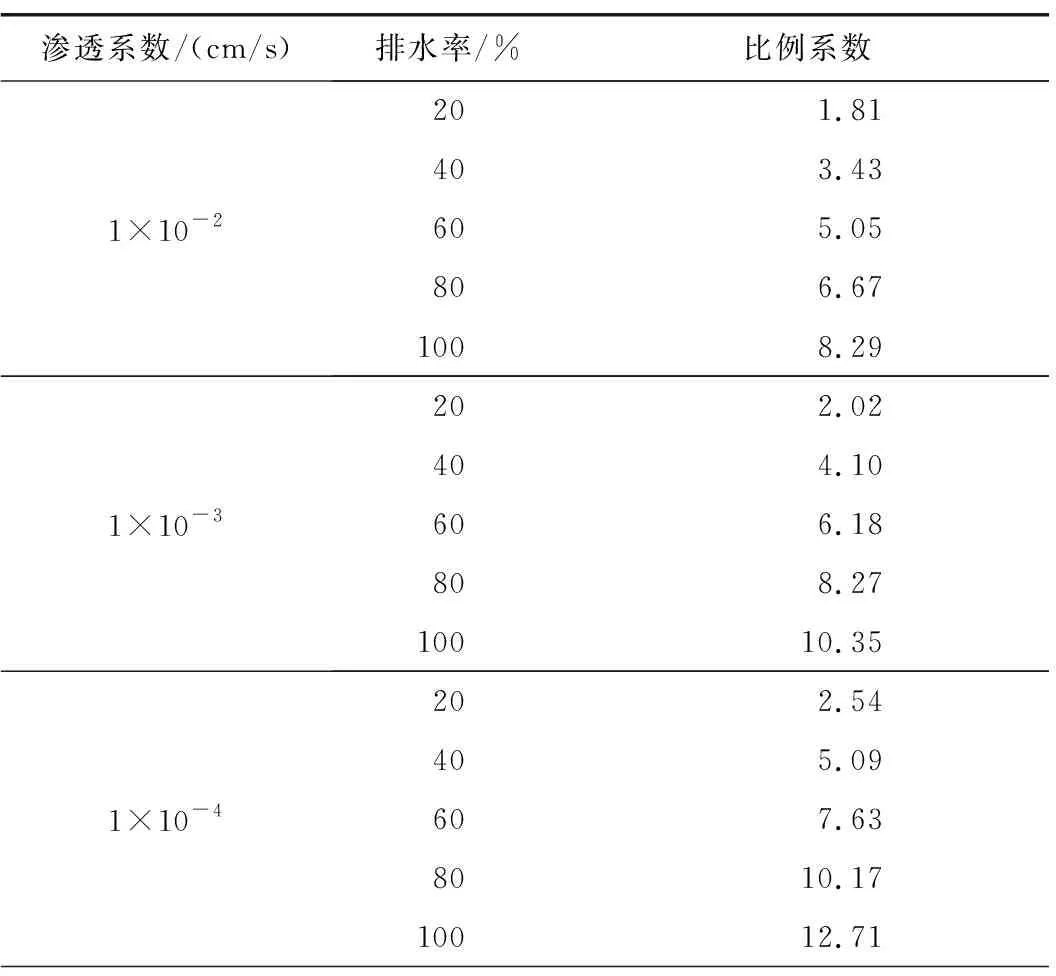
表4 不同工况下比例系数表

表4(续)

比例系数与渗透系数、排水率拟合云图如图10所示。可以看出： 比例系数与排水率、渗透系数呈二次曲面关系，且拟合相关系数为99.78%，拟合结果良好。因此，可采用式(5)对比例系数进行计算。

图10 比例系数与渗透系数、排水率拟合云图

a=1.6+0.44lnk+3.5β×10-2+2.9(lnk)2×

10-2-0.01βlnk。

(5)

式中a为比例系数。

因此，当水头高度小于等于临界水头高度时，围岩渗流扰动高度可按式(2)计算，其中比例系数按式(5)计算。

5 围岩渗流扰动高度计算方法室内试验验证

为了验证本文所提出的围岩渗流扰动高度计算方法的正确性及合理性，采用室内相似试验，模拟富水深埋隧道排水条件下围岩渗流场扰动变化过程，获得相应围岩扰动高度，并将其与采用计算方法所得结果进行对比。

5.1 室内相似材料准备

选取几何相似比、容重相似比、渗透系数相似比为基础相似比，根据相似三定律[16]，推导出其余相似试验所需物理量的相似比例关系。室内试验所需物理量相似比如表5所示。

围岩相似材料为石英砂与石膏粉的混合料，其中混合料组分比例根据模型试验渗透系数工况要求确定，以保证围岩相似材料渗透系数满足试验工况渗透系数要求。围岩相似原材料如图11所示。

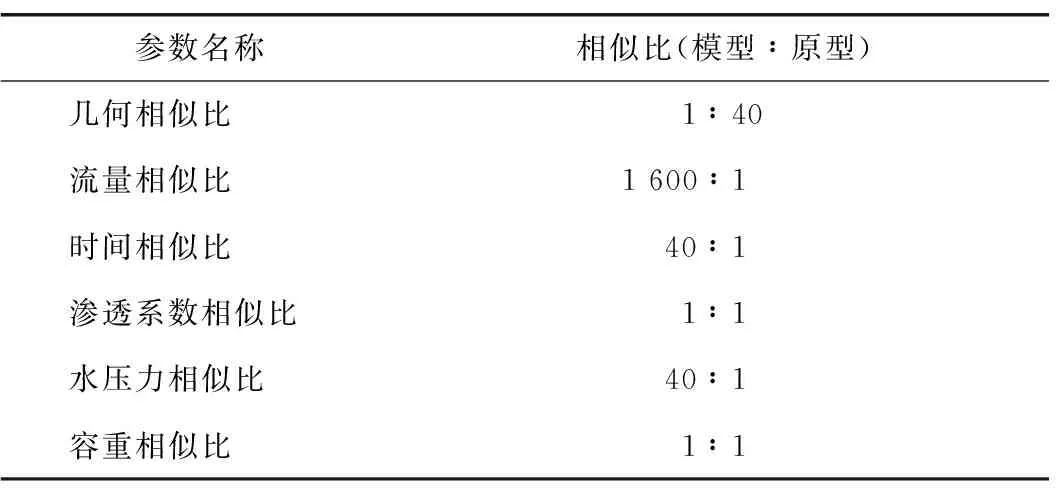
表5 室内试验所需物理量相似比

(a) 石英砂 (b) 石膏粉

衬砌结构相似材料为PVC圆形管状材料，衬砌相似结构尺寸为原型结构按几何相似比缩尺后的相应尺寸。同时，在管片相似结构上开孔，以实现衬砌结构排水。通过控制管片结构开孔数量，可实现不同排水率条件下的管片衬砌排水过程。管片相似结构如图12所示。

(a) 相似管片外侧

(b) 相似管片内侧

5.2 试验工况

结合室内试验条件，制定了3种不同渗透系数试验主要工况，且水头高度均为90 m。其中，每种主要工况下分别细分3种排水率工况。室内试验模拟工况如表6所示。

表6 室内试验模拟工况

5.3 试验装置及测点布置

5.3.1 试验装置

本次试验在西南交通大学自行设计的大型富水深埋隧道渗流场模拟试验系统上进行，整套试验系统由环境箱(4 m×0.7 m×4 m)、控制系统、数据采集系统3部分组成。渗流模拟试验系统如图13所示。渗流场控制系统由测压管和水平平行进、排水花管组成。数据采集系统包括TS-KY-1型高精度微型孔隙水压力传感器、静态数据采集仪、隧道排水采集箱等，实现对隧道周边渗流场扰动的监测。

(a) 模型试验

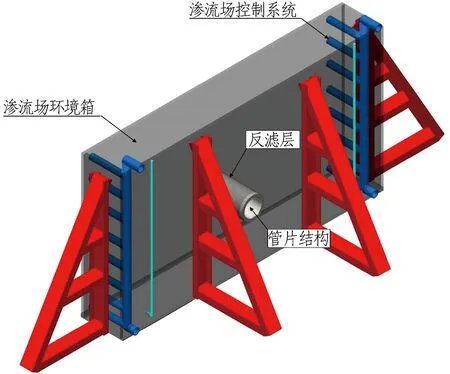
(b) 试验装置示意图

5.3.2 测点布置

选择沿隧道轴向方向中间位置断面作为监测断面，以水平间隔25 cm(约1倍隧道洞径)布设5根纵向测管；每根纵向测管以垂直间隔20 cm布设渗流压力测点(所用仪器为微型水压力计)；同时，管片衬砌背后环向方向亦布设相应测点。室内模型试验测点布置如图14所示。

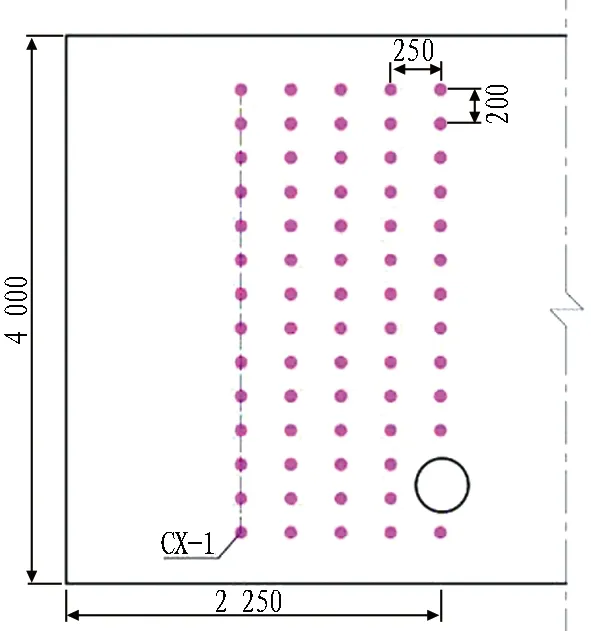
5.4 试验过程

1)采用配比好的石英砂与石膏粉的围岩相似材料，将环境箱填筑密实；同时在隧道标高处安装衬砌管片。

2)采用渗流场控制系统，对环境箱进行注水，使其达到试验所需的稳定渗流场条件。

3)根据不同排水率细分工况，对管片衬砌开孔进行控制，并在试验过程中实时采集围岩渗流场以及隧道排水量数据。

4)将管片衬砌进行拆除，测量该主要工况下隧道涌水量；进而，计算得到隧道排水率。室内模型试验过程如图15所示。

5.5 试验结果验证分析

将本次不同试验工况条件下得到的围岩渗流扰动高度与采用上文提出的围岩渗流扰动高度计算方法计算所得的结果进行对比分析。围岩渗流影响高度计算结果对比如图16所示。

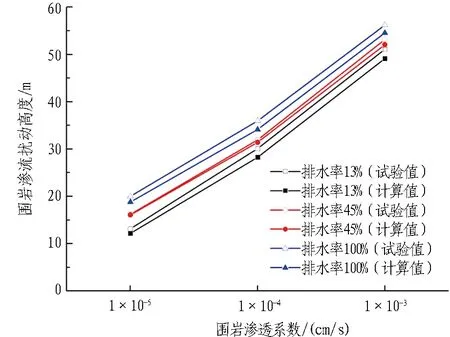
图16 围岩渗流影响高度计算结果对比

由图16可知: 1)给定排水率条件下采用2种方法得到的围岩渗流扰动高度均随渗透系数增加而呈现增加趋势，2种方法反映的对应一致； 2)通过对比给定排水率与渗透系数条件下采用2种方法获得的围岩渗流扰动高度量值可知，2种方法所得结果较为接近，差异较小，从而验证了上文所提的围岩渗流扰动高度计算方法的正确性及合理性。

6 结论与建议

1)富水深埋隧道排水泄压过程会对隧道拱顶上方围岩渗流场产生明显扰动，隧道上部围岩渗流压力等势线分布由水平分布形态转变为漏斗状分布形态。但这种隧道排水扰动仅在隧道拱顶上部一定范围内存在，将该扰动范围的纵向高度定义为围岩渗流扰动高度。

2)围岩渗透系数、水头高度以及隧道排水率均与围岩渗流扰动高度呈正相关关系。通过对围岩渗流扰动高度影响程度对比可知，排水率是产生围岩渗流场扰动的根本因素，但其对围岩渗流扰动高度影响最小，影响程度最大的因素为围岩自身的渗透系数。

3)当给定渗透系数与排水率时，随水头高度增加，围岩渗流扰动高度变化呈2段式变化特征。当水头高度小于等于临界水头高度时，围岩渗流扰动高度与水头高度呈线性正相关关系；当水头高度大于临界水头高度时，围岩渗流扰动高度不再随水头高度继续变化，趋于定值。

4)采用数理拟合方法，分别给出了临界水头高度、临界围岩渗流扰动高度计算表达式；根据水头高度与围岩渗流扰动高度相互关系，给出了围岩渗流扰动高度计算方法；并采用室内相似试验对所提计算方法进行了对比，验证了所提计算方法的正确性及合理性。

本文在计算衬砌背后水压力量值时，所用方法相对较为简单，与实际存在一定差别，下一步建议探讨衬砌背后各点水压力的计算方法。