基于Brent算法的轴偏置虎克铰型Hexapod平台位置反解
2021-07-03孙佳霖刘曰涛杨梦超付连壮
孙佳霖,刘曰涛,杨梦超,韩 振,付连壮
(山东理工大学 机械工程学院,山东 淄博255049)
1 引言
Hexapod并联平台也称作并联六自由度平台,其基本构型最早由英国工程师Stewart提出。经过几十年的发展,Hexapod平台凭借控制精度高、结构刚性好、负载能力强、工作稳定性高等特点,被广泛应用于光学领域[1-2]、主动隔振[3-4]、运动模拟[5]及自动对接等领域。目前,Hexapod平台也是大型光电望远镜次镜调整机构以及空间相机隔震系统的主要构型形式。位于智利的VISTA(Visible and Infrared Survey Telescope for Astronomy)望远镜[6],LSST(The Large Syn⁃optic Survey Telescope)望 远 镜[7],中 国“天 眼”FAST望远镜[8]以及詹姆斯•韦伯空间望远镜(JSMT)等均采用了Hexapod并联平台作为自身重要调整机构。
Hexapod并联平台主要构型形式包括6-SPS,6-UPS,6-UCU(S,P,U,C分别代表球铰、移动副、虎克铰、圆柱副)等[9-11]。由于望远镜调整机构的整体趋势是向着高刚度高稳定性方向发展,所以球铰的负载能力和运动间隙成为了其主要制约因素[12]。同球铰相比,虎克铰在损失了一定工作空间的前提下,提高了结构整体稳定性和控制精度。同时,为了进一步提高虎克铰的刚性,Gloess[13]等 提 出 了 轴 偏 置 虎 克 铰 结 构,使 得Hexapod并联平台具有更好的结构刚性和稳定性。
Hexapod并联平台的位置反解是根据动平台的位置姿态求解驱动腿长度的过程,不同结构形式的Hexapod平台,其位置反解算法的难易程度也不同。球铰和十字交叉轴虎克铰结构均具有唯一确定的旋转中心,且旋转中心在相对坐标系下不发生改变。因此,6-SPS型,6-UPS型或6-UCU型Hexapod平台的位置反解可以通过解析法直接求解[14-15]。由于轴偏置虎克铰结构具有两个垂直且不相交的旋转轴,因此,运动链的长度不仅与直线驱动部件有关,而且与轴偏置虎克铰结构的位置姿态有关。同时,轴偏置虎克铰作为从动件,无法确定两旋转轴的转动角度,所以该类型平台的位置反解无法通过解析法直接求得,只 能 采 用 数 值 法。Dalvand[16]等 针 对6-RRCRR(R表示转动副)型并联平台,利用闭环矢量法建立了运动链的非线性方程组,并通过Newton-Raphson法对方程 组进行求 解。Yu[17],Han[18]等对该算法控制下的并联平台进行了运动学分析和测试。该方法虽然可以解决轴偏置虎克铰型Hexapod平台的位置反解问题,但是在工程实际应用中,大量的位置反解计算对平台响应速度影响较大。因此,对于双端轴偏置虎克铰型Hexa⁃pod平台的位置反解还需要寻求既快又准的计算方法。
本文针对双端轴偏置虎克铰型Hexapod平台,提出了一种新的位置反解算法。首先,利用空间向量法构建了基于空间圆辅助模型的运动学模型;然后,结合Brent法求解平台位置反解的数值解,并对丝杠螺母产生的衍生运动误差进行了补偿;最后,建立位置正解模型并搭建实验样机,以验证所提出算法的准确性和可靠性。
2 Hexapod平台理论模型
2.1 轴偏置虎克铰结构
虎克铰结构具有承载能力强、结构刚度高、运动间隙小等特性,被广泛应用于各种并联机构的转动关节。但是典型的十字轴虎克铰结构,构型较为复杂,十字交叉轴的设计对于加工和装配都是巨大的考验。因此,提出了虎克铰结构的优化形式——轴偏置虎克铰结构,如图1所示。两转轴R1,R2分别与平台和驱动腿连接,并通过轴承与转动块铰接。相比较于十字轴虎克铰,该结构具有更高的刚度、强度和更大的工作空间,且两转轴和转动块相互分离的设计方案,更有利于保证加工精度和装配误差。
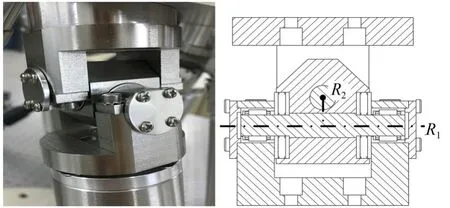
图1 轴偏置虎克铰结构Fig.1 Axis offset Hooke joint
2.2 平台模型
双端轴偏置虎克铰型Hexapod平台由动平台、定平台、6根驱动腿和12个轴偏置虎克铰组成,驱动腿由滚珠丝杠和驱动电机等部件组成。据此,Hexapod平台的理论模型可视为动定平台通过6根RRCRR运动链连接的并联机构,如图2所示。
轴偏置虎克铰位于动、定平台的铰点Ri1和Ri4(i=1,2,…,6)分别构成了两个不同的基准圆,称为动基准圆和定基准圆。位于动基准圆和定基准圆上的铰点均围绕120°基准线对称分布。为描述平台的运动位姿,分别定义基坐标系OB,工作坐标系OW和工具坐标系OT。基坐标系OB位于定准圆圆心,与定平台固接,ZB轴始终垂直于定基准圆所在平面且指向动平台方向。工作坐标系OW始终位于基坐标系ZB轴方向H处,指向与基坐标系相同,不随平台运动而变化。平台位于零点状态时,工作坐标系原点与动基准圆圆心重合。工具坐标系OT固接于动平台,随动平台的运动而运动,坐标原点与动基准圆圆心重合。因此,铰点Ri4(i=1,2,…,6)在基坐标系下的位置向量BR i4(i=1,2,…,6)可表示为:
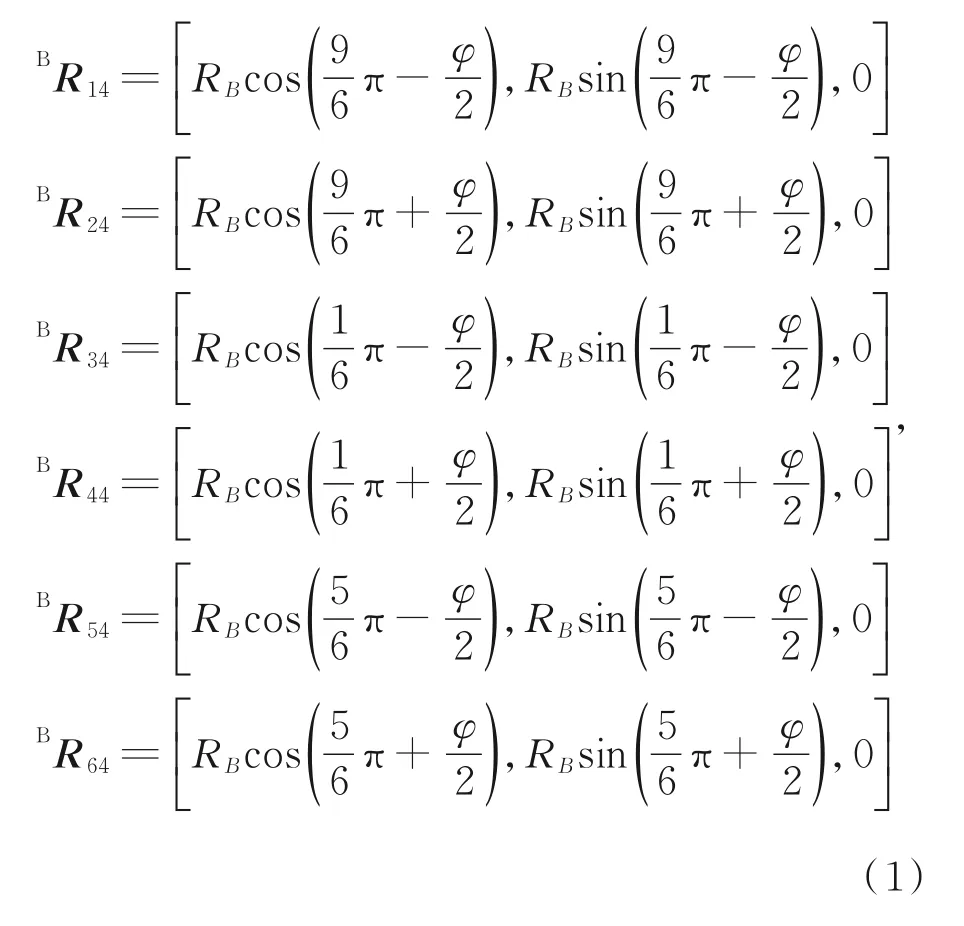
其中:φ表示定平台上相邻两铰点间的夹角,RB为定基准圆半径,如图2所示。
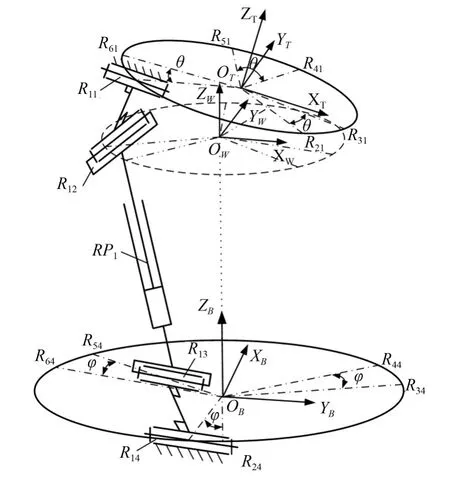
图2 Hexapod平台理论模型Fig.2 Theoretical model of hexapod platform
铰点Ri1(i=1,2,…,6)在工具坐标系下的位置向量TR i1(i=1,2,…,6)可表示为:
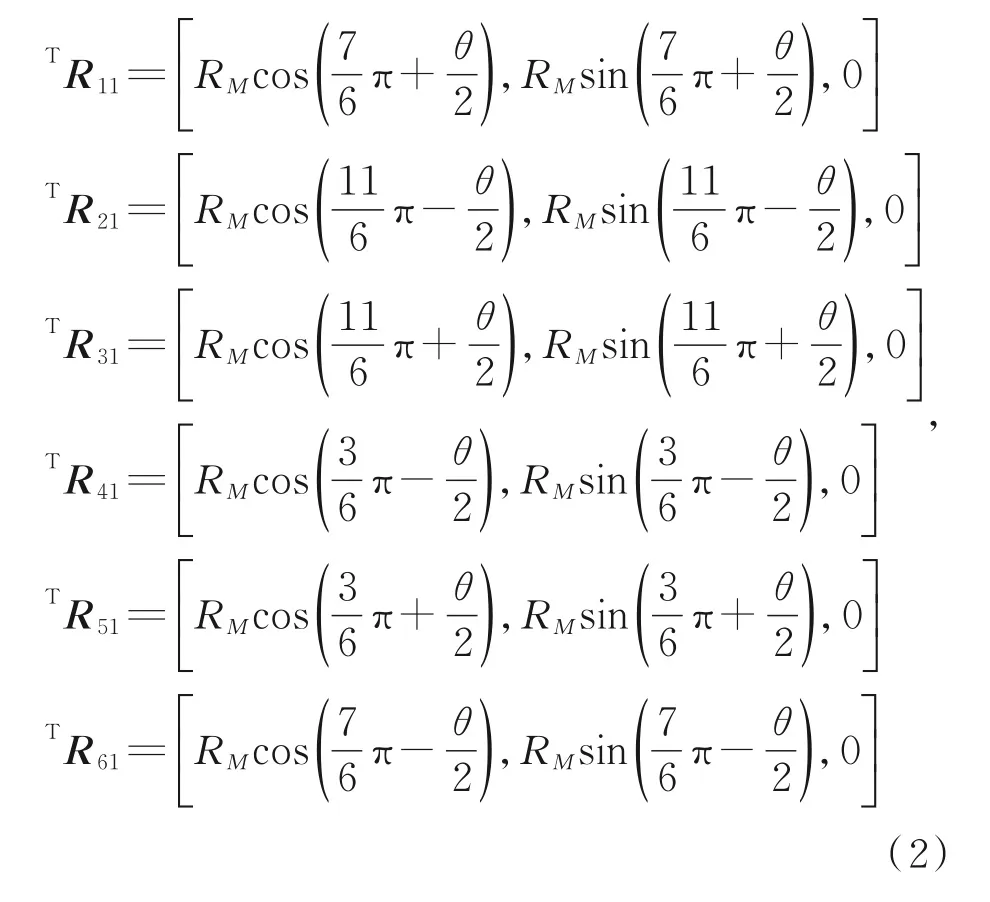
其中θ表示动平台上相邻两铰点间的夹角,如图2所示。
3 Hexapod平台位置反解算法
3.1 位置反解基本算法
机构的位置分析是机构速度分析、加速度分析、受力分析、动力分析和机构综合等分析的基础,它包括位置正解和位置反解两部分。位置正解是根据输入端的输入参数求解输出端的位置和姿态的过程;反之根据输出端的位置和姿态求解输入端参数的过程则是位置反解。因此,由平台理论模型可知,驱动腿的长度可表示为(如图2所示):
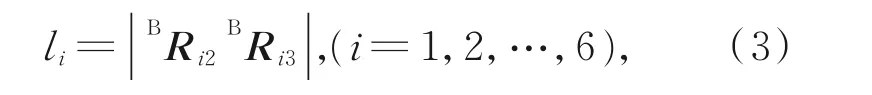
其中:BR i2和BR i3(i=1,2,…,6)分别表示铰点Ri2和Ri3(i=1,2,…,6)在 基 坐 标 系OB下 的 位 置向量。
根据所建立的坐标系,动平台的位置和姿态可表示为矢量[x,y,z,u,v,w]T。其中,[x,y,z]T表示工具坐标系OT在工作坐标系OW下的位置,[u,v,w]T表示动平台分别绕工具坐标系XT,Y T,ZT轴的旋转角度。工具坐标系OT相对于工作坐标系OW的姿态变换则用RPY组合变换来表示。因此,可得工具坐标系OT相对于工作坐标系OW的变换矩阵:

通过坐标变换方法,可得铰点Ri1(i=1,2,…,6)在基坐标系下的位置向量:

由Hexapod平台的理论模型可知,轴偏置虎克铰的两个转动量均属于未知量,所以无法通过解析法求得驱动腿的长度。分析轴偏置虎克铰的运动特性可知,一个铰点始终围绕另一个铰点在同一平面内做圆周运动。以铰点Ri1(i=1,2,…,6)为圆心,偏置距离e为半径,作辅助圆C1,其法向量N i1(i=1,2,…,6)与上转轴轴心重合。以铰点Ri4(i=1,2,…,6)为圆心,偏置距离e为半径,在下转轴的垂面内作辅助圆C2,其法向量为N i4(i=1,2,…,6),如图3所示。因此,驱动腿长度li可等价为空间中两个圆的最短距离,进而将位置反解求解问题等效为空间中两圆最短距离的求解问题。David[19]提出了求解空间中圆与直线、圆与圆的距离求解方法。
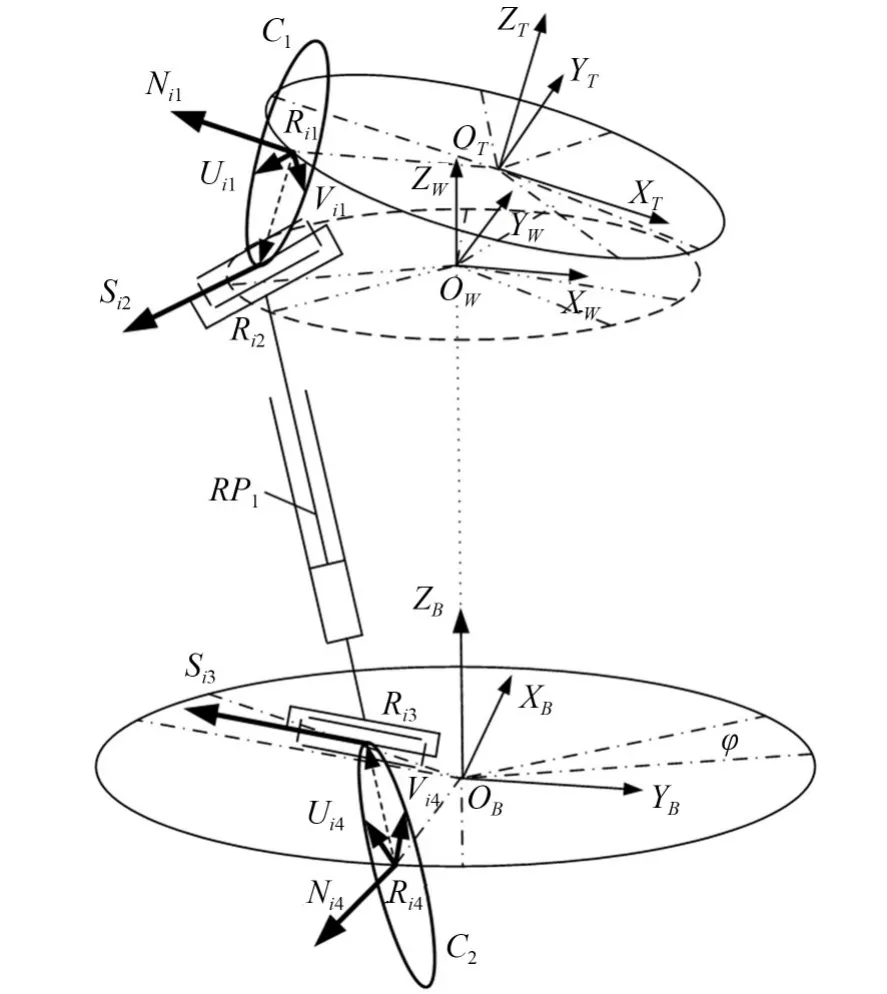
图3 Hexapod平台辅助圆模型示意图Fig.3 Schematic diagram of auxiliary circle model of hexapod
为建立空间中任意两圆的距离公式,首先,假设空间中任意点向量P,点P至圆C2的距离可表示为:
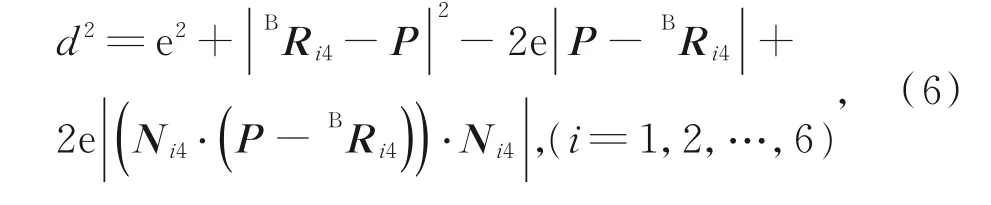
其中N i4为空间圆C4的法向量。
空间圆C1可表示为:
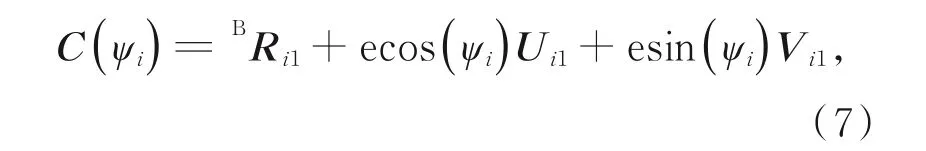
式中i=1,2,…,6,U i1和V i1为空间圆C1的任意两个单位向量。
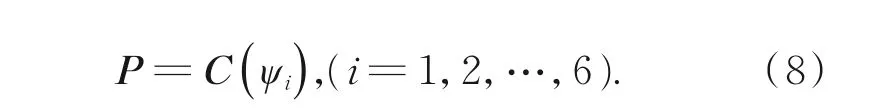
令联立公式(6),(7)和(8),得空间圆C1和空间圆C2的距离公式:
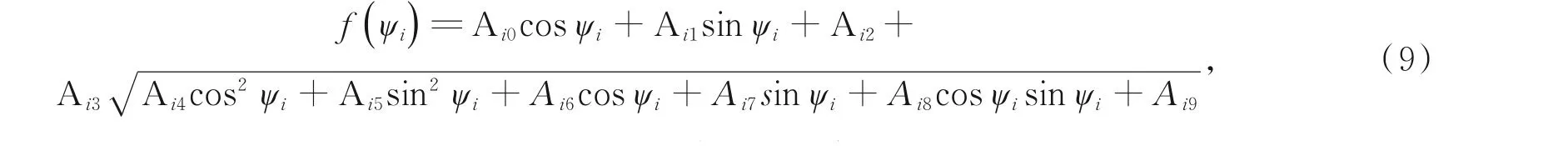
式中:
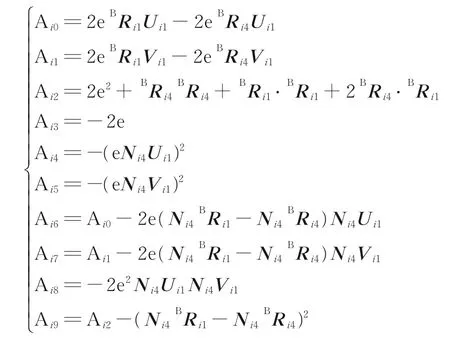
其中i=1,2,…,6。驱动腿长度可表示为:
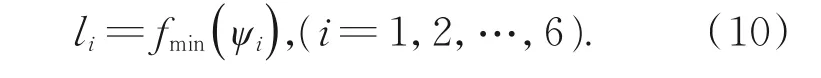
因此,可利用公式(9)的导函数对最小值进行求解。
3.2 衍生运动补偿
本文所涉及双端轴偏置虎克铰型Hexapod平台,驱动单元包括滚珠丝杠和驱动电机等部件。其中,滚珠丝杠具有两个相互耦合的自由度,包括螺母的直线运动和旋转运动。螺母的直线运动作为主动运动,由电机直接控制,为可控运动。螺母的旋转运动作为驱动腿的第6个自由度,需要配合动平台完成运动。然而,螺母的旋转运动会导致驱动腿长度发生变化,且无法通过驱动装置直接控制。因此,该运动被定义为衍生运动,需要在主动运动的基础上进行衍生运动误差补偿。从而驱动腿的实际长度可表示为:
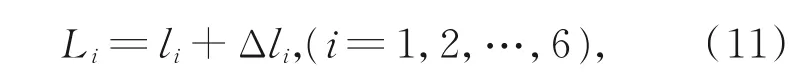
其中:li定义为伸缩腿理论长度,Δli是由螺母的旋转运动所产生的衍生运动误差。
定义铰点Ri1,Ri2,Ri3,Ri4的旋转轴向量分别为S i1,S i2,S i3,S i4,根据图2所示的驱动腿结构示意图可知:
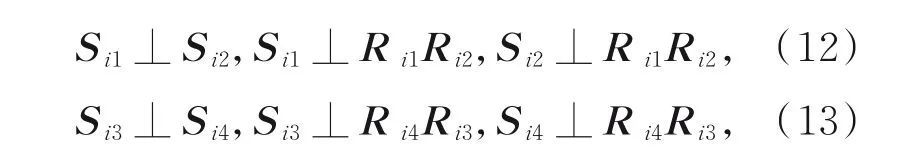
其中i=1,2,…,6。
将位置反解求得的ψi值代入公式(5)可得铰点Ri2的位置向量,根据空间中点到圆的最短距离可求得Ri3的位置向量。又因S i1=N i1,S i4=N i4。向量S i2和S i3可表示为:
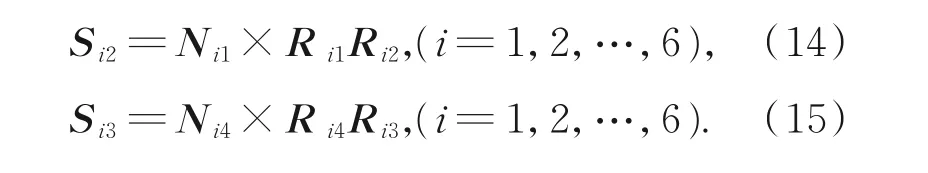
到达目标位置时,螺母转动的角度可表示为:
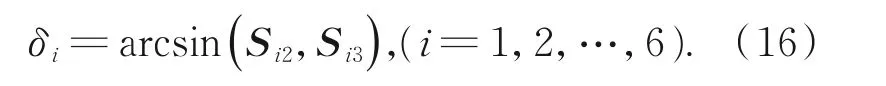
因此,由螺母的旋转运动所产生的衍生运动误差为:
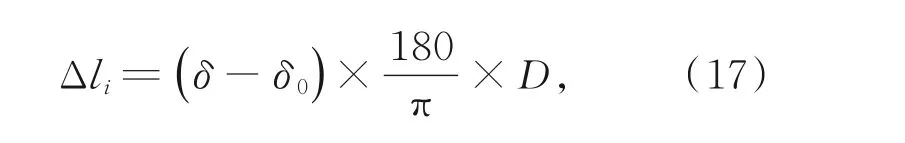
其中:δ0为平台位于初始状态时S i2和S i3的夹角,D为丝杠的导程。
4 Brent算法
Brent方法是一种结合二分法、割线法和反二次插值方法的寻根方法[20]。二分法则是不断对区间[a,b]进行二等分,利用端点对零点进行逼近,即下次迭代的初值可表示为:

割线法是根据有根区间内a,b两点所构造弦的斜率代替目标函数的切线斜率,将割线与横坐标的交点作为方程的近似根。即给定区间内两点(a,f(a)),(b,f(b)),建立割线方程:
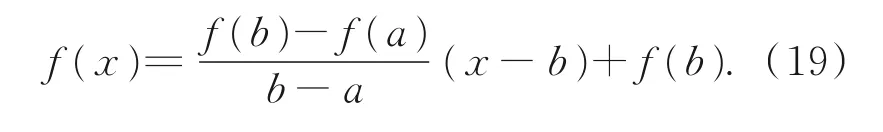
令f(x)=0,则下次迭代的初值为:
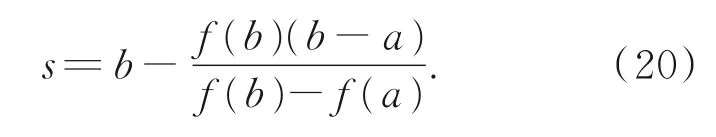
反二次插值类似于割线法,是根据区间中三个点(a,f(a)),(b,f(b)),(c,f(c))确定一个二次函数,并将二次函数与纵坐标的交点作为下次迭代的初值:
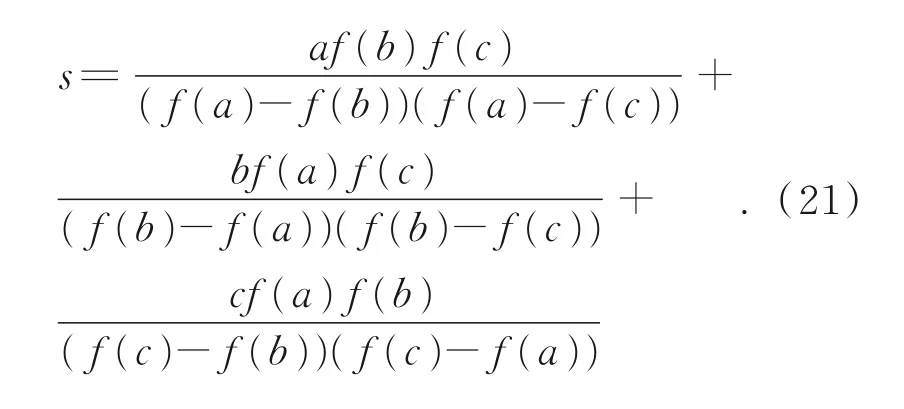
Brent法的核心是选择尽可能快的方式求根,如果生成的结果超出了估计值范围,则转为相对保守的二分法,即使二分法的收敛速度比较慢,但可以有效的将生成的根估计值锁定在边界以内,如果生成了可以接受的根则转为更快的反二次插值法或割线法。
Brent算法的计算流程,首先初始化区间(a,b),使得f(a)f(b)<0,并满足|f(a)|>|f(b)|。每次迭代的初值包括ak,bk,bk-1,bk-2(ak为第k次迭代的左估计值,bk为右估计值,其中k=0,1,2,…)。|ε|>|bk-bk-1|且上次迭代为二分法(ε为迭代精度);|s-bk|>且上次迭代为二分 法;|ε|>|bk-1-bk-2|且 上 次 迭 代 不 是 二 分法;|s-bk|>-bk-2|且上次迭代不是二分法;,bk)且上次迭代不是二分法,若满足以上条件的任意一个则本次迭代采用二分法。若采集点满足f(ak)≠f(ck)≠f(bk),则采用反二次插值,否则采用割线法。
5 Brent算法在Hexapod并联平台位置反解中的应用
Brent算法在Hexapod并联平台位置反解中主要应用于求解铰点Ri2,Ri3的位置向量,流程图如图4所示,具体计算流程如下:
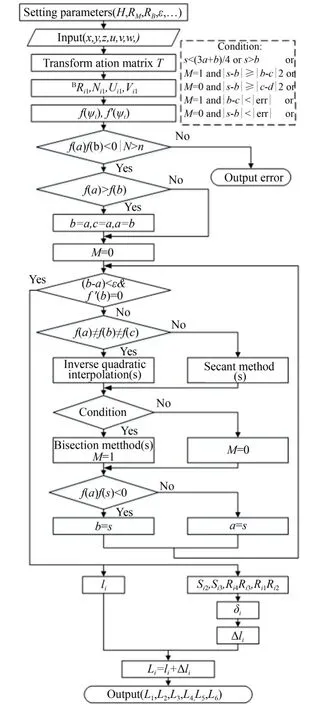
图4 Hexapod平台位置反解流程图Fig.4 Flowchart of inverse kinematics of Hexapod plat⁃form
(1)给定平台初始参数,包括H,φ,θ,RM,RB等。预设当前计算精度ε,迭代初值ψ0,最大迭代次数N;
(2)输入目标位姿(x,y,z,u,v,w);
(3)求解变换矩阵T;
(4)根据坐标变换方法,求解各铰链变化后的位置向量、法向量、单位向量TR i1,N i1,U i1,V i1;
(5)建立空间圆距离公式f(ψi);
(6)求解距离导数公式f′(ψi);
(7)判断区间(a,b)是否有根且迭代次数小于N,如果是转至步骤(8),否则转至步骤(19);
(8)根据f(b)及f(a)值的大小判断是否交换端值,并令c=a,设置标志位M=0;
(9)判断有根区间大小是否小于迭代精度ε,或f′(b)=0,如果是转至步骤(15),否则转至步骤(10),进入Brent算法;
(10)判断f(a),f(b),f(c)是否相等,是转至(11),否转至(12);
(11)利用反二次插值求解,得下次迭代值s;
(12)利用割线法求解,得下次迭代值s;
(13)判断是否符合二分法求解条件(第4章介绍),若符合,采用二分法求得下次迭代值s并使标志位置1,否则标志位置0;
(14)根据f(a)*f(s)的值重新分配有根区间。迭代次数增加并返回步骤(9);
(15)将求得的ψi值带回到空间圆距离公式f(ψi),求得驱动腿理论长度li;
(16)求解铰点Ri2,Ri3的位置向量,并根据向量叉乘原理求解法向量S i2,S i3;
(17)求解衍生运动误差Δli;
(18)得到驱动腿实际长度L i;
(19)迭代终止,无解或超出最大迭代次数。
6 实验与测试
搭建Hexapod并联平台实验样机,其结构参数为,H=330 mm,φ=9°,θ=19°,RM=150 mm,RB=315 mm,e=13 mm,D=1。驱动腿运动范围:285~360 mm。运动空间:x=±20 mm,y=±20 mm,z=±25 mm,u=±5°,v=±5°,w=±8°。该构型在其工作空间内无奇异点。
在Windows7操作系统,Intel(R)Xeon(R)CPU E3-1225 v5@3.30 GHz 3.31 GHz处理器,8.00 GB内存的电脑上,利用Matlab(R2016b)对Newton-Raphson法和Brent法位置反解算法进行编程。迭代精度均设置为δ=0.00001,最大迭代次数N=10000。
随机选取工作空间中的任意5组位姿(如表1所示),并利用Newton-Raphson法和Brent法分别进行位置反解求解,迭代次数和迭代时间如表2所示。分析表2可知,虽然Newton-Raphson算法的迭代次数较少,但是其消耗的计算时长远大于Brent法。这是由于基于Newton-Raphson算法的位置反解求解方法,需要利用闭环矢量法对同一运动链建立两个不同的约束方程,且需求解至少12个转换矩阵和6个Jacobian矩阵[16-17]。因此,在计算的复杂程度上,基于Newton-Raphson算法的求解方法要高于采用Brent算法的求解方法。
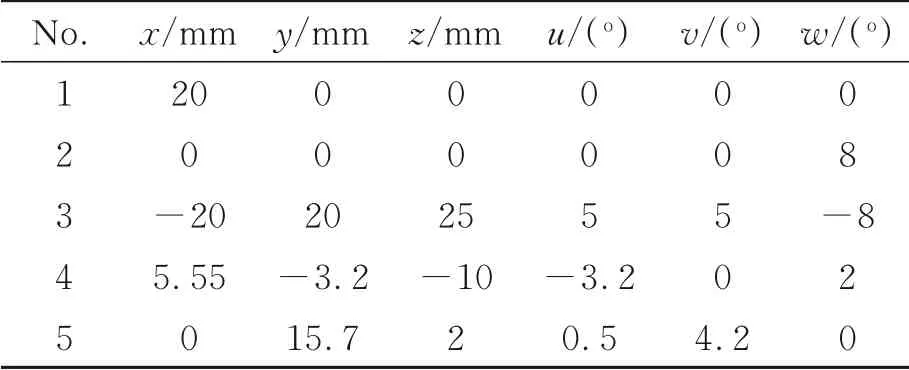
表1 随机选取5个位姿Tab.1 Five randomly selected poses
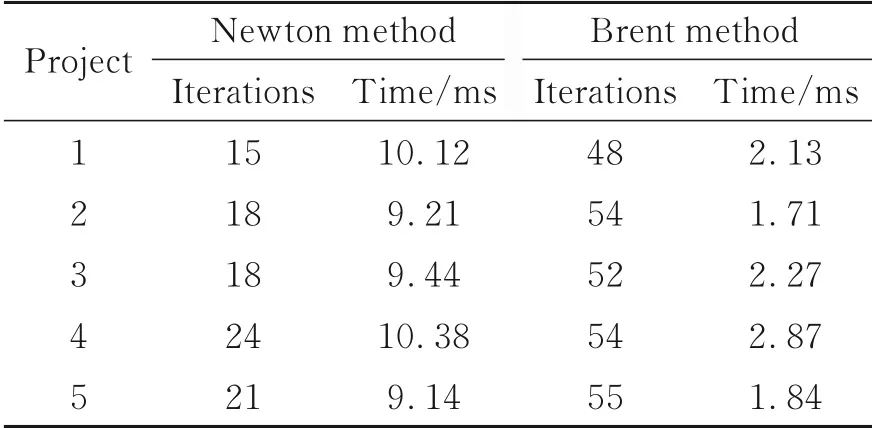
表2 迭代次数和迭代时间对比Tab.2 Comparison of iteration number and iteration time
为验证本文所提出算法的准确性,参照已有的位置正解算法[21],对该平台进行位置正解建模。将位置正解算法作为反馈机制,用来实时检测平台的运动轨迹。设定平台运动路径为:
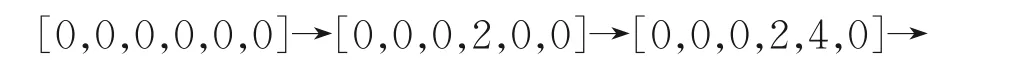
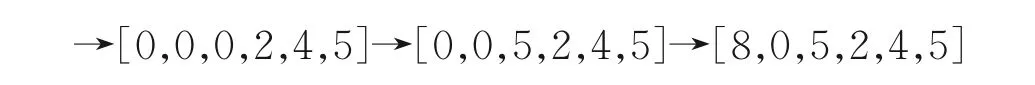
计算位置反解,并将计算结算结果作为位置正解的输入量,求解平台的实时位姿,结果如图5所示。
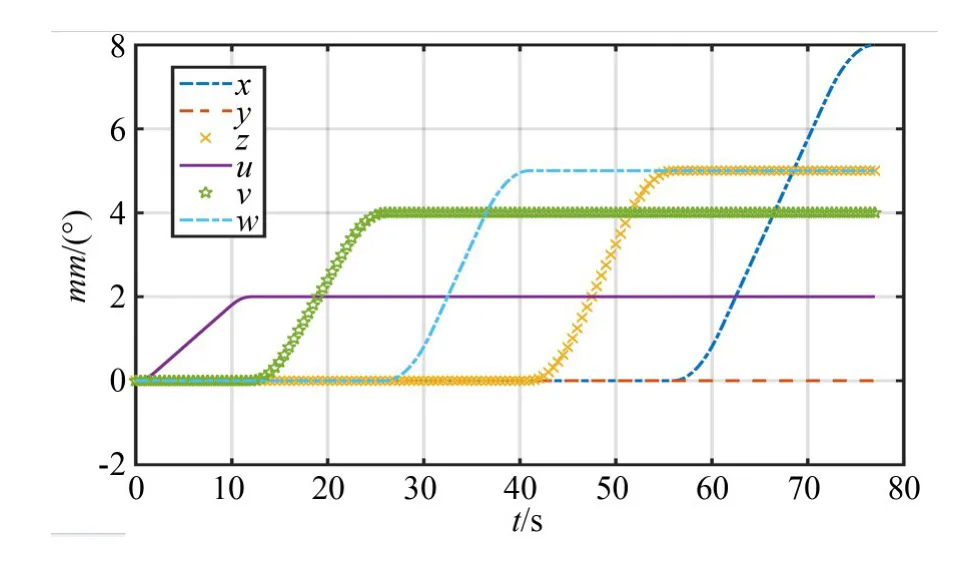
图5 Hexapod平台位姿变化Fig.5 Pose changes of the Hexapod platform
根据以上实验路径,对衍生运动误差补偿前后的驱动腿长度误差和平台位姿误差进行分析。由图6可见,驱动腿长度误差可达到0.015 mm。分析图7,由Hexapod平台的位置正解模型反馈回的动平台位姿状态可知,衍生运动产生的腿长误差,不仅会引起目标自由度的位置或角度偏差,而且其他自由度也会产生较大偏差,且误差超过0.01 mm/0.36"。因此,对于高精度Hexapod平台,衍生运动误差补偿环节是必不可少的。
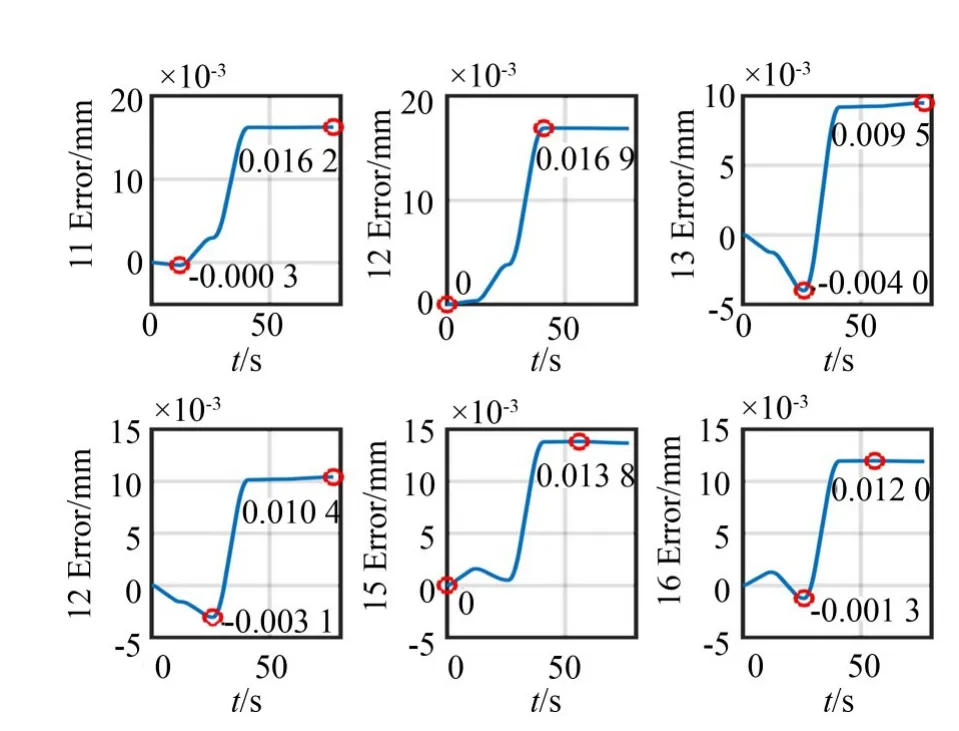
图6 Hexapod平台驱动腿长度误差Fig.6 Leg length error of hexapod platform
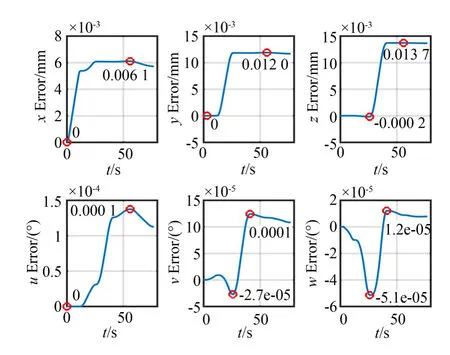
图7 Hexapod平台位姿误差Fig.7 Pose error of hexapod platform
按照以上实验路径,对实验样机的响应速度进行测试,在不改变平台硬件设施,以及轨迹规划、路径规划、运动学正解等计算程序的前提下,仅对比两种不同求解方法(基于Brent法和基于Newton-Raphson法)控制下实验样机的响应速度。到达每一目标位姿时程序执行位置反解子程序的次数,以及从发送指令到平台移动之前所消耗的时长均记录于表3。分析表3可知,在相同计算次数下,基于Brent算法法控制下的Hexapod平台响应速度比基于Newton-Raphson算法控制下的平台响应速度高出约0.5 s(含硬件设备的性能、通讯的延迟时间等因素)。因此,基于Brent算法的并联六自由度Hexapod平台位置反解有效改善了该类型平台的响应速度。

表3 平台响应速度对比Tab.3 Comparison of platform response speed
同时,采用Renishaw XL-80激光干涉仪对实验样机进行打表测试,以验证平台仍保持有微米级和角秒级控制精度。选取重复精度较差的x轴和u轴进行重复精度测量,并按照ISO 230-2标准进行重复定位精度计算。测量结果选取4倍标准差作为该测量轴的重复定位精度。测量结果如图8~图9所示。测试结果显示移动轴单向重复定位精度可达2.0μm且转动轴单向重复定位精度可达1.5。
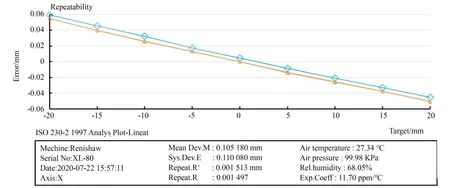
图8 x轴重复精度测量结果Fig.8 x-axis repeatability measurement results
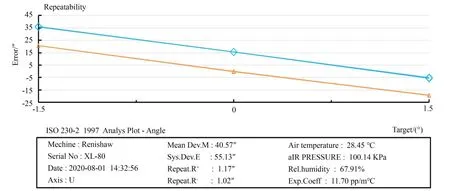
图9 u轴重复精度测量结果Fig.9 u-axis repeatability measurement results
7 结论
本文针对双端轴偏置虎克铰型并联六自由度Hexapod平台提出了一种基于Brent算法的位置反解求解方法。该方法建立了一种基于空间圆辅助模型的运动学模型,并利用Brent法对非线性方程组进行数值求解,从而在保证计算精度的同时提高了运算速度。通过实验与测试对所提出算法的有效性和准确性进行了评估,实验结果表明,基于Brent算法的位置反解算法运算时间优于Newton-Raphson算法,且该控制算法下的实验样机在保证精度的同时平台综合响应速度提高了约0.5 s。
