用问题的弦拨动初中学生数学思维的键
2021-07-03江苏省南通市海门区正余初级中学袁健风
江苏省南通市海门区正余初级中学 袁健风
教师在数学教学的过程中,要激发学生的思维,让他们在课堂中充分展示自己。教师可通过不同的方式设置不同的问题,进而进一步拨动学生思维的弦,使他们迸发出更多的思维火花,获得更多的素养生长。
一、在导入环节设置问题,引发学生思维
教师在导入环节要先提出问题,让学生在问题中思考。导入的目的就是让学生思考起来,让他们进入本课要学习的内容。教师设置一定的问题,学生就会沿着问题去发现一些新的问题,进而渐渐启发思维。以人教版初中数学八年级下册“等腰三角形的性质与判定”为例,教师先让学生将书中的内容浏览一下,让他们大致知道这一课要学的性质或者原理是什么,用这些认知能解决什么样的问题,接着设置这样的题目:如图1 所示,在△ABC中,AB=AC,D在BC上,且AD=BD,AC=CD,求∠B的度数是多少。学生会想:这样的问题一定要运用到本节课的认知,于是先将书本中获得的信息进行整理,比如:等腰三角形的性质—两个底角相等;如果一个三角形有两个角相等,那么这两个角所对的边也相等。接下来,学生就试着运用这些新的认知去发现一些新问题。首先学生想到:由AB=AC是不是可以推断∠B=∠C?由AC=CD是不是可以推断∠CAD=∠CDA?由AD=BD是不是可以推断∠B=∠BAD?他们再进一步地提出问题:由∠CDA=∠B+∠BAD是不是可以推断出∠CAD= ∠CDA=2 ∠BAD;∠BAC=3 ∠BAD=3 ∠B?学生想到这一步的时候,思维似乎僵化了,教师提醒他们思考某一个角。学生揣摩着图形想到这样的问题:是不是要求的∠BAC可以通过∠B来转换?他们从“三角形内角和为180°”得出∠BAC+∠B+∠C=180°,进而得出5 ∠B=180°,于是∠B=36°,自然就有了∠BAC=108°。可见,在导入环节,教师要设置问题,进而引发学生的一连串问题,学生的问题会交织着思维的迸发。
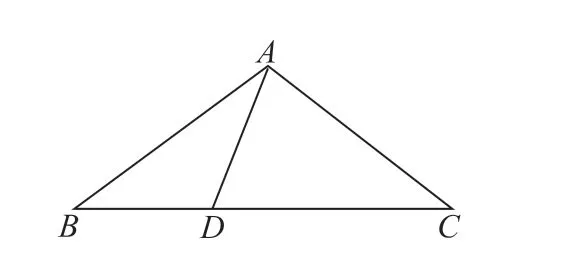
图1
二、在合作环节设置问题,激活学生思维
教师可以让学生在合作中解决问题。如果面对一个大的问题,学生感到无处下手,教师可设置恰当的小问题,让合作贴近学生的认知水平。仍以人教版初中数学八年级下册“等腰三角形的性质与判定”为例,学生在做下面这道题的时候出现了不同的答案,教师让学生在合作中发现了存在的问题。题目如下:等腰三角形的周长为14,其中一边长为6,则另两条边长分别是多少?教师将学生分成六人小组,每个学生依次讲述自己的做题思路,当所有学生都表述完自己的思路,学生就基本知道自己错在哪儿了。接着,教师抛出这样的问题:如果遇到类似的题目,需要怎样去做?能不能再创建一道题目?换言之,学生要再次合作去思考一般的规律。学生先是将题目完整地解答出来,再在合作中展示自己的体验,也是为了更好地发言。学生发现做这样的题目需要进行分类讨论,这也是他们在合作中获得的新的数学思想。当然,每个学生都见识了别人创建的题目,他们又会对这些题目进行相关的分析,思维进一步被激活。
三、在拓展环节设置问题,提升学生思维
学生在学习数学的过程中需要不断地往思维的纵深处发展,即需要进行深度学习,这需要教师创设拓展环节。还以“等腰三角形的性质与判定”为例,教师设置这样的题目:如图2 所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点。求证:AF⊥CD。学生将题目中的条件在图上标出来,他们发现,要证明AF与CD垂直,如果连接AC、AD,是不是只要证明AC=AD就可以了?要证明这两条线段相等,是不是只要证明△ABC≌△AED?这样的证明对学生来说没有太大的难度,教师要进一步提升他们的高阶思维能力,要让他们学会猜想、推测、判断、推理、迁移等,于是提问:能不能发现新的结论?这其实需要学生自己去发现问题,再去解决问题,需要学生综合多方面的认知。学生从第一题中获得灵感:连接AC、AD,就有新的收获;如果连接BE后,会不会有什么新的结论?学生在连接之后,凭直观去猜测BE跟CD可能平行,BE与CD可能垂直,学生要做的就是去证明自己的猜想。这个环节中,教师给学生更自主的空间,学生不但要解题,还要自己创建题目。
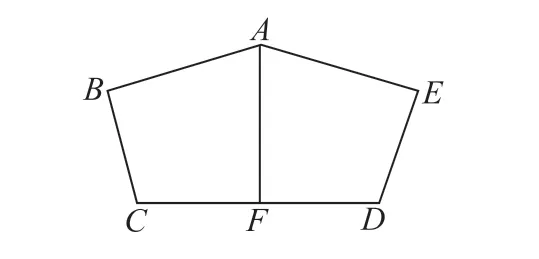
图2
总之,教师在教学的过程中不仅仅要教授相关的数学知识,还要培养学生的思维能力。当课堂围绕问题开展,学生的思维自然就汩汩而出。
