边缘凸起式超显微硬度压痕的共聚焦测量
2021-07-02张凯林侯晓东
石 伟,张凯林,侯晓东
(1. 中国航空工业集团公司北京长城计量测试技术研究所,北京100095;2. 北京航空航天大学仪器科学与光电工程学院,北京100191;3. 东莞材料基因高等理工研究院应力测量技术研究所,广东东莞523808)
1 引 言
随着科技的发展及新材料的不断涌现,产品的多样化发展和质量控制水平对硬度测量及校准提出了越来越高的要求,其中对新材料微小力及微压痕超显微硬度领域的测试问题尤为突出。微观硬度由于特别适用于微小、薄型试件及脆硬试件的测试,对金属组织、金属表面加工层、电镀层、硬化层、热处理试件、碳化试件、光纤维、碳纤维和陶瓷等材料的校准测试有着特殊的需求和研究意义。
超显微硬度压痕是介于显微压痕和纳米压痕之间的硬度压痕,超显微硬度压痕的特点为:其对角线长度在5~20 μm 之间;载荷、加载速度及保持时间可控,载荷在10 gf~300 gf。
随着超显微硬度测量需求的增多,要求也越来越高。目前,常用的显微硬度计采用传统的光学成像来测量压痕大小,由于成像分辨率的限制,往往不能满足显微硬度压痕尤其是超显微硬度压痕的测量。另外,传统的光学显微镜仅能够得到压痕的二维投影数据,然后通过测量压痕对角线计算试样的硬度;但是在一些情况下,试样材料的不均匀或杂质的存在使得压痕边缘产生不规则的变化,呈现不规则的凸起结构,对测量结果的影响较大[1]。
在科研和工程实践中,对小试件尤其是薄膜、涂层等材料的显微硬度测量的常用方法是仪器化压入试验(通常被叫做纳米压痕仪)。和常规的硬度测量相比,仪器化压入技术可以记录整个压入过程中的试验力-位移曲线,并根据Oliver-Pharr 方法利用卸载部分的载荷-压深关系曲线计算出等效接触面积,从而求出材料的压痕硬度[2]。仪器化压入试验的最大特点是不需要直接测定压痕大小,仅通过载荷-压深关系曲线和压头面积函数即可得到硬度和其它材料的力学参数,尤其适用于受限于光学成像分辨率的纳米硬度测量[3]。但是仪器化压入试验机相对于传统硬度仪的设备成本和维护成本都更高,而且对于相关技术人员的要求也高,其工业应用受到了一定程度的限制。除此之外,仪器化压入测量中的接触面积是通过压头面积函数和压入深度计算得到的,一般不会考虑压入过程中压痕周围所产生的凸起或凹陷,对于一些特定材料的硬度测量会存在误差[4]。因此,有必要针对超显微压痕的三维形貌进行精确测量以获得微观硬度,并在此基础上和仪器化压入测量得到的硬度值进行对比分析。由此可见,常用的微小压痕测量装置包括显微维氏测量装置和纳米压痕仪都不能满足边缘凸起式的超显微压痕的测量。为实现对角线小于20 μm 的边缘凸起式超显微压痕的测量,本文采用分辨率更高的激光扫描共聚焦显微镜(Laser Scanning Confocal Microscopy,LSCM)对压痕进行测量,得到了压痕的全面三维形貌数据,更准确地表征材料的硬度。
在压痕等微观结构的形貌测量中,人们已经应用LSCM 辅助观察压痕的形貌。Cheng[5]等通过LSCM 观察硅样品和碳化硅样品,比较压痕在微观结构形态上的不同。Li[6]等研究球压头尺寸对布氏硬度的影响,利用LSCM 观察球形压痕的三维形貌。Jong[7]通过LSCM 对压痕进行测量,并提出了通过体积参数计算洛氏硬度的模型。Hou[8]等比较了光学显微镜、原子力显微镜和LSCM 的测量结果的优缺点和不确定度,并提出了一种压痕处理方法来区分球形压痕的接触内点区域和外点区域。综上所述,目前共聚焦显微技术一是辅助观察不同材料压痕的结构形态,二是用于测量球形压痕;而对于边缘凸起不规则的维氏四棱锥压痕的测量研究却很少。
使用高分辨率的LSCM 测量边缘凸起不规则四棱锥压痕的一个关键问题是基准平面的确定。本文对不同基准平面的判定标准开展研究,计算相对应的压痕有效区域和硬度,并与对角线测量方法得到的超显微硬度值进行对比,得到了符合硬度测量规律的基准平面判定方法。通过比较不同硬度值的硬度块的测量结果,验证了该基准平面的有效性。
2 测量原理
LSCM 是在传统光学显微镜上加装激光扫描装置,对试样焦平面上的每一点进行扫描,逐点逐层测量试样上的点。物镜的衍射分辨率为:

式中:λ为波长,NA为物镜的数值孔径,k为系数。在这个光路中,只有处于焦平面位置的光能穿过探测针孔,焦平面以外的光则被小孔过滤掉,使得非观察点的背景呈黑色,反差增大,成像清晰,可减小k的值,有效提高LSCM 的分辨率[9-11]。此外,LSCM 采用逐层扫描的设计,不仅具有较高的横向分辨率(可达到0.3 μm),还具有较高的纵向分辨率(可达到20 nm),所以各层扫描的图像也较为清晰。
LSCM 测量的压痕为三维立体结构,且试样并不是理想的均匀材料,在压痕边缘会产生不规则的凸起,因此,确定三维压痕的边缘非常重要。
2.1 超显微硬度测量原理
超显微硬度属于压入硬度法,将顶部两相对面为136°的正四棱锥体金刚石压头用试验力压入试样表面,保持规定时间后,卸除试验力,测量试样表面压痕。超显微硬度通过测量压痕对角线长度d进而计算压痕表面积,最后求出压痕表面积上的平均压力,即有:
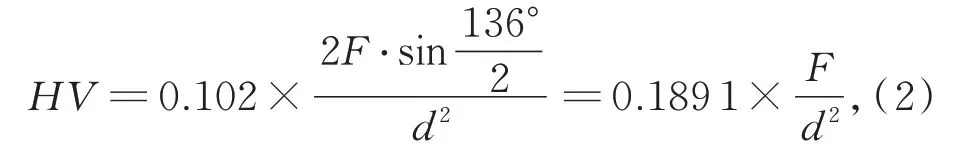
式中:HV为超显微硬度;F为压入载荷;d为压痕对角线长度[12]。
2.2 压痕对角线法
为提高超显微硬度的测量准确性,充分发挥LSCM 测量三维压痕的优势,测量三维压痕的角点位置,通过试验力与三微压痕的对角线来计算硬度。
以压痕最低点所在轴为平面的旋转轴,取矩形截面,该截面与压痕的交线即为压痕的截面曲线。三维压痕的截面如图1 所示,横轴为压痕点与轴线的距离X,纵轴为压痕点的高度Z,提取截面中的极值点,极值点位置可从一阶微分图2 中得到,即微分快速变化并接近零值的点。极值点左边的部分为压痕部分(即压头部分和被测材料的接触部分),极值点右边的部分没有和压头直接接触,去除极值点右边与压痕无关的部分,实现压痕的提取,选择压痕截面的极值点作为压痕的边缘。充分利用LSCM 在Z轴高分辨率的特点,可以精确取到压痕的边缘最高点,作为压痕的边缘,之后进一步从压痕边缘中筛选出4 个角点(p1,p2,p3,p4),即可根据超显微硬度的定义计算硬度值。
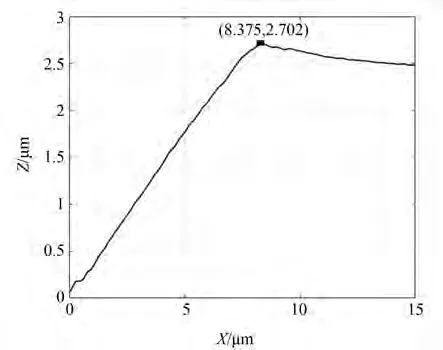
图1 压痕截面Fig.1 Cross section of indentation
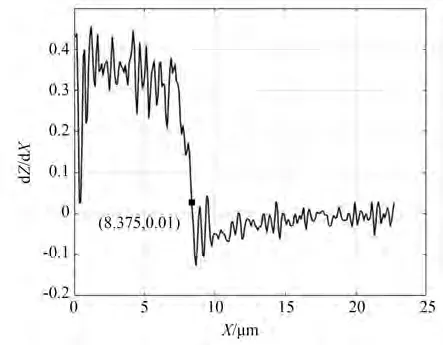
图2 压痕的一阶微分Fig.2 First-order differential of indentation
2.3 基准平面法
压痕产生过程如图3 所示。原始试样平面为h0,压头加载到最大载荷时的压痕深度为hm,此时的试样与压头的接触位置的高度为hc。当载荷卸载后压痕产生弹性回复,残余压痕各面更接近球形曲面,其中残余压痕的凸起高度为hb。
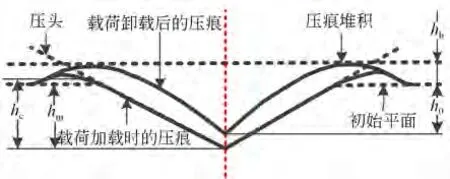
图3 压痕产生过程示意图Fig.3 Schematic diagram of indentation production process
超显微硬度的传统计算中,假定压痕为理想的标准四棱锥,但是实际测试得到的压痕会由于塑性变形的不均匀性而偏离此假定(如图3 所示),而且压痕边缘往往会产生凸起或凹陷。此方法还采用最高边缘位置来确定压痕大小,但是实际的压头和被测材料的最后接触点(即hc所对应的接触点)往往低于最高边缘,这也意味着传统的基于压痕对角线的硬度测量方法和硬度定义本身有着不小的偏离:对于压痕边缘产生凸起的材料,测量得到的硬度值低于实际硬度值,而对于边缘产生凹陷的材料则会相反。综上所述,通过对角线计算硬度值的方法过于简单,忽略了压痕本身的形貌和边缘信息,所确定的硬度值与硬度的基本定义有所差别[13]。LSCM 测量硬度压痕的方法可以获得压痕的三维数据信息,为进一步分析压痕接触面积提供数据支持,因此,尝试寻找更符合接触力学规律的压痕接触面积计算方法。
本文针对具有边缘凸起特征的压痕测量,基准平面定义为确定接触面积所对应的平面,即压头和被测材料最高接触点所对应的平面,见图4。假设最优的基准平面为Pr平面,Pr下方的区域为有效压痕区域,若Pr上方仍有压痕数据,则Pr上方的区域为打压试样过程中产生的无效凸起,即无效压痕区域。本文的目标就是求得符合接触力学规律的基准平面Pr。
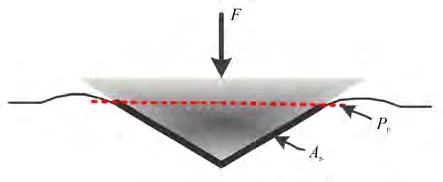
图4 压痕基准平面示意图Fig. 4 Schematic diagram of indentation datum plane
根据接触力学规律,均匀介质的接触面积函数应均匀变化,试样与压头接触部分随着压入深度h的增加,接触部分的面积应呈现一定的规律,即接触面积函数。当h到达基准平面以上的部分时,面积函数呈现不同的规律,所以可以通过微分方程确定接触面积增长变化的拐点,而该拐点即为最优基准平面的位置[8,14]。
测量的压痕为三维立体结构,在压痕边缘会产生不规则的凸起。使用压痕点云分割方法将压痕区域分割出来。设定基准平面,逐层切削三维压痕模型,可得到不同高度对应的面积函数。基准平面与试样平面平行,表示如下:

式中:(a0,a1,a2)为试样平面的法向量,以压痕尖端的点为零点,h为基准平面与尖端的距离。寻找最优基准平面的问题可以转化为寻找最优基准平面高度的问题。
基准平面h的迭代公式为:
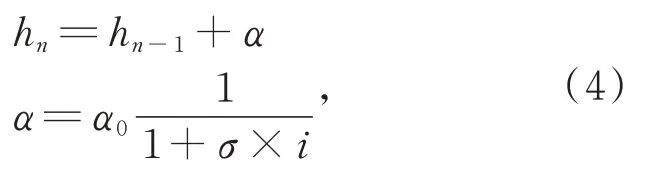
式中:α为学习率,σ为衰减因子。随着迭代次数的增加,学习率不断下降,所以开始时应使用较大的学习率,以加快收敛速度,防止发生震荡;而在接近压痕基准平面位置的时候采用较小的学习率,以更准确更快地得到不同高度对应的压痕面积。
3 实验结果及分析
3.1 实验及压痕提取
测试试样选择硬度检定中常用的钢试样,硬度块选择硬度值在200~800 HV 的不同硬度值钢硬度块,硬度块为硬度测量中常用的GCr15 钢材料标准块。利用共聚焦显微镜测量不同硬度值的压痕形貌。显微压痕实验载荷采用500,300,200 和100 gf,获得压痕对角线大于等于20 μm 的压痕,从而获得试样的基准硬度。力加载装置为北京长城计量所的MV-1000 显微硬度计,如图5 所示。超显微压痕实验载荷根据硬度的不同采用200,100,50,25 和10 gf 打压试样,可以得到5~20 μm 的压痕。

图5 MV-1000 显微硬度计Fig. 5 MV-1000 microscopic vickers hardness tester
数据采集设备采用奥林帕斯OLS-5000 型LSCM(如图6 所示)。测量使用的物镜的数值孔径NA 为0.95,测量视场为128 μm×128 μm,采集点数为1 024×1 024,测量的层析高度设置为0.12 μm。测量过程中首先要确定包含整个压痕形貌的扫描高度范围,然后通过激光逐点逐层扫描试样采集数据,获得各层的数据之后对所有数据进行包络拟合,得到压痕的三维数据集合,即测量区域范围内(包含压痕)的每一点的三维坐标。

图6 奥林帕斯OLS-5000 型激光共聚焦显微镜Fig. 6 OLS-5000 laser scanning confocal microscope
激光扫描共聚焦显微镜测量得到的压痕为试样表面上每一点的三维数据,包括每一点的坐标,如图7 所示。压痕提取的实现过程首先进行滤波,去除压痕数据中明显偏离试样的离散点云数据。其次,图7 所示以压痕最底端的四棱锥尖端点P所在的Z轴为旋转轴,以垂直于压痕表面的平面作为旋转平面,旋转360°。每一个旋转平面与压痕点云数据的交线,提取该交线的极大值点即拐点作为分割点,分割点左边的数据即为压痕区域数据,分割点右边的数据即为试样平面区域数据。对压痕数据与旋转平面的每一个交线做分割操作[15],即可提取完整压痕区域数据。
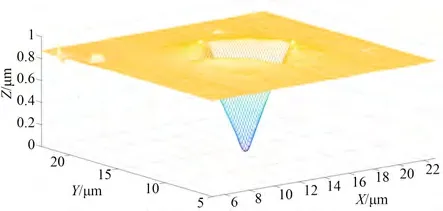
图7 压痕测量实验三维数据Fig. 7 3D data of indentation in measurement experiment
该方法提取的压痕区域数据为试样中整个压痕数据,如图8 所示。压痕区域包括压痕的内点和压痕的边缘点,通过提取压痕边缘确定压痕边缘上的4 个角点,得到压痕对角线的长度,从而与传统的显微硬度测量方式一致,实现了小于20 μm 的超显微硬度的测量[15]。
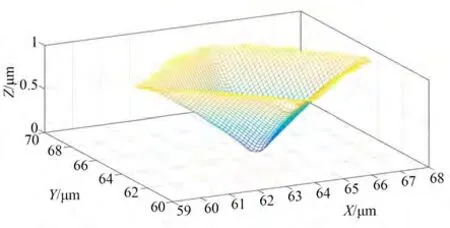
图8 提取的压痕区域Fig.8 Extracted indentation area
3.2 压痕对角线法测量结果
通过试样与垂直平面的截面提取压痕区域,通过提取边缘获得压痕4 个角点的位置,进而得到压痕的对角线长度。通过式(1)的施加载荷和对角线长度得到试样的超显微硬度,分别进行不同硬度以及不同载荷的超显微测量实验,可以看到实验结果与显微硬度结果基本一致。但在个别点有差别,当压痕较小时硬度变化较大,其原因主要包括压痕尺寸效应、材料不均匀和测量误差等[16]。
如表1 所示,显微硬度值与超显微硬度值的差别较小,可以大体表征试样的硬度值。造成该偏差的根本原因是测量方式不同,图9(a)所示为显微硬度测量压痕的2D 投影,利用像素之间的对比度来提取边缘进而测量对角线长度;共聚焦测量压痕的3D 形状,截面高度对比如图9(b)所示,提取极值点位置作为边缘。虽然都是通过对角线计算硬度值,但成像原理和分辨率的不同从根本上决定了显微硬度和超显微硬度的差别。
3.3 基准平面法测量结果
测量的压痕为三维立体结构,由于试样并不是理想的均匀材料,压痕边缘会产生不规则的凸起,如图7 所示。受边缘的凸起和下沉以及打压过程中的弹性变形和塑性变形的影响,上述超显微测量中对角线计算压痕表面积的方法必然具有误差。因此,为准确获得有效的接触面积,设计基准平面的概念如图4 所示,并寻找最优的基准平面来准确获得压痕的有效接触面积。
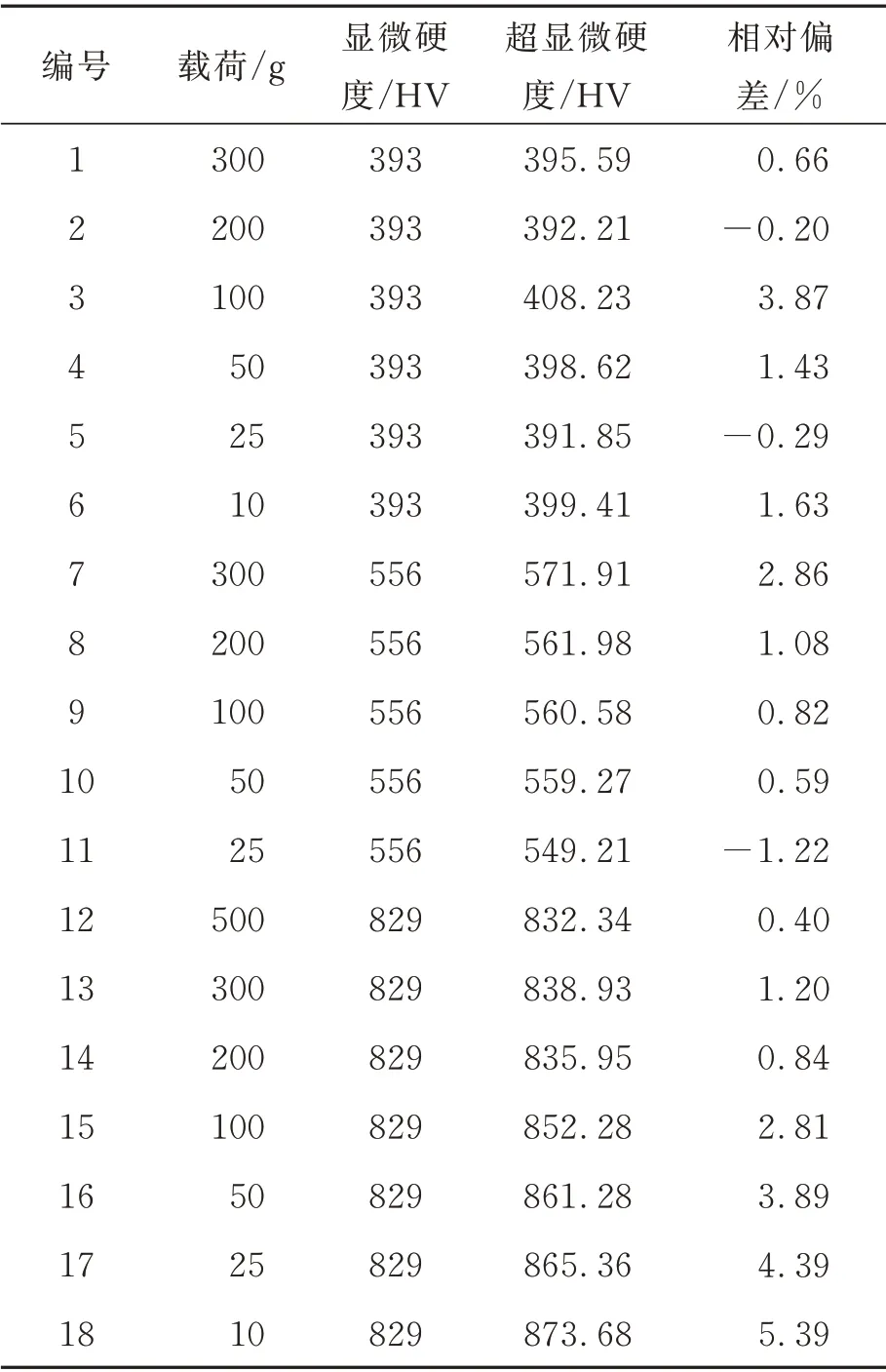
表1 压痕对角线法测量结果Tab.1 Measurement results of micro-hardness by indentation methods
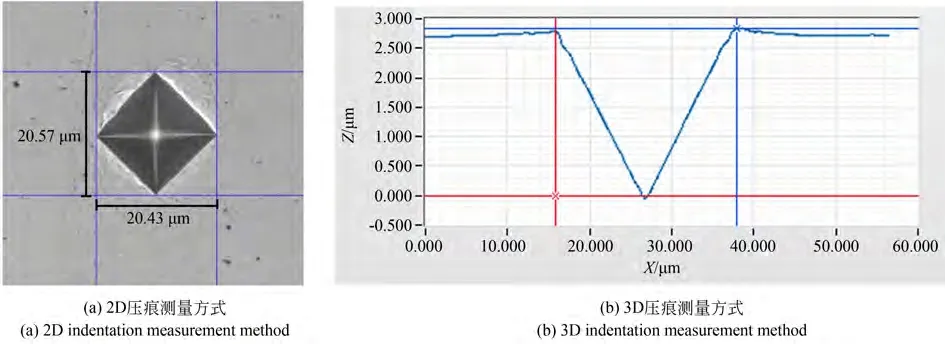
图9 显微硬度测量结果Fig. 9 Measurement result of micro-hardness
实验采取的压头是夹角为136°的四棱锥,与试样接触的平面均为平面。根据接触力学的规律,一个受载的钢塑性材料包含发生塑形流动的区域和基于刚性假设的无变形区域,被四棱锥挤出的塑性流动区域的材料凸起在压头的两边,所以形成如图6 所示的边缘凸起,但凸起部分并不都与压头接触。假定压头为标准的四棱锥,那么与压头接触的面积应呈现一定的函数关系,称为接触面积函数,即有:

式中:S为压痕面积,hi为基准平面的高度。
通过公式(4)逐步迭代截取不同高度的压痕,获得不同高度所对应的接触面积,从而拟合出接触面积函数。当截取高度为压痕的非接触部分时,接触面积会发生突变,这一高度为接触部分的临界节点,所对应的截取平面为最优的基准平面,即更符合接触力学规律的基准平面。
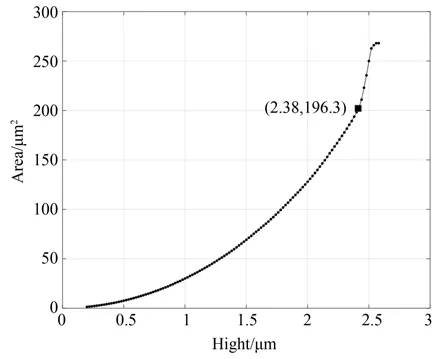
图10 压痕的面积函数Fig.10 Area function of indentation
设定不同高度的平面截取压痕,得到高度与面积的函数曲线如图10 所示。可以看到,随着高度的上升,面积呈二次多项式增长,但存在一个拐点使得高度上升,面积的增长趋势发生变化,该拐点即为最优基准平面的位置。对该函数进行一阶微分,得到:

一阶微分函数如图11 所示。
图11 中为面积函数散点图的一阶导数,可以很明显看到在高度小于拐点(2.38,196.3)的位置,面积函数的一阶导数基本呈现线性变化,该变化符合面积函数为二次多项式的变化规律,在大于高度h1点时面积函数的一阶导数变化增大。
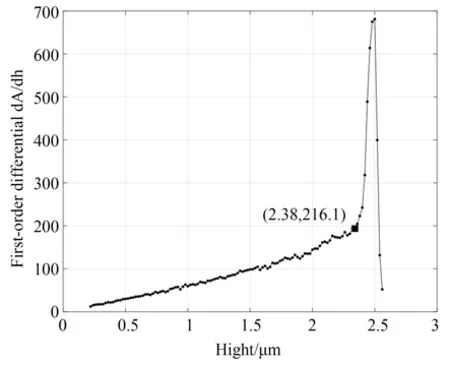
图11 面积函数的一阶微分Fig.11 First derivative of area function
对面积函数求二阶导数,得到:

二阶导数如图12 所示,可以看到在同样高度二阶导数的变化也较剧烈,说明该点的高度为符合接触力学变化规律的接触面积的基准平面高度。
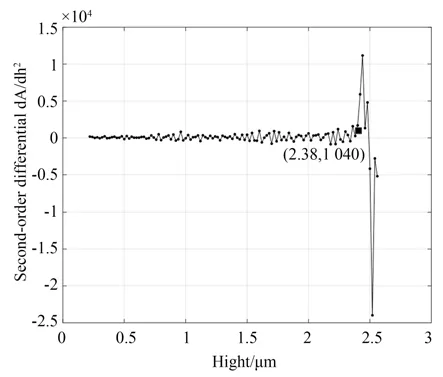
图12 面积函数的二阶微分Fig.12 Second derivative of area function
分别选取不同硬度的硬度块在相同条件下进行重复测量。在同一硬度块上施加相同的载荷打压试样,在相同条件下使用共聚焦显微镜测量压痕的最优基准平面的位置和相对应的压痕的表面积,试验结果如表2 所示。对于不同硬度块进行多次测量,测量值与平均值的差值在±1.5%以内,不同硬度块的测量实验的相对标准差在1%以内。实验表明,最优基准平面测量得到的硬度值的误差小于±1.5%,且测量稳定性小于1%。实验结果表明,基准平面法可以较稳定地测量得到压痕的硬度。目前,关于小于20 μm 的压痕,并没有硬度测量真值,而基准平面法从定义出发,且实验稳定性较好,该实验结果可以更好地反映微小压痕条件下的试样硬度。
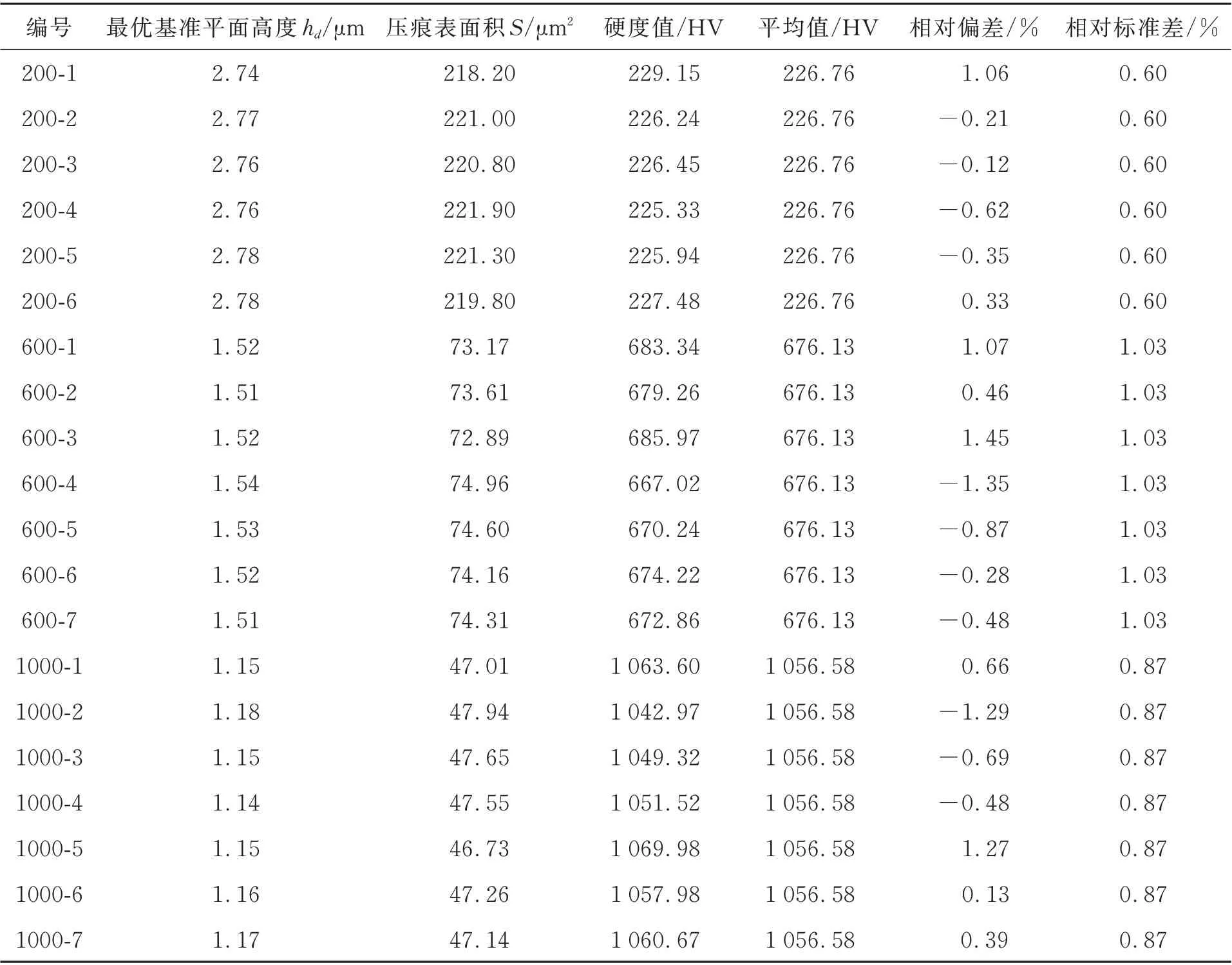
表2 基准平面法硬度测量结果Tab.2 Hardness measurement results by datum plane method
通过计算压痕的最优基准平面得到接触表面积的方法虽然可以准确得到硬度值,但该方法操作复杂,且和传统的硬度测量结果偏差较大。因此,考虑到操作复杂度以及硬度结果的重复性,在实际工程中对于超显微压痕的测量建议仍采用四角点测量对角线,进而计算硬度值的方法。最优基准平面测量硬度值的方法作为更接近真实硬度值的理论方法,可在后续工作中进一步深入研究。
4 结 论
本文在LSCM 测量得到的三维数据的基础上,提出了一种有别于传统测量方法的显微硬度测量方法。该方法充分发挥了LSCM 高精度、高分辨率、较高的纵向分辨率和轴向分辨率的特点,通过对压痕三维形貌数据进行滤波和边缘提取,提取压痕角点,并计算超显微硬度值。基于共聚焦的超显微三维压痕测量过程如下:(1)选择载荷F打压试样,共聚焦测量压痕的三维数据;(2)提取压痕区域;(3)提取压痕的4 个角点,计算压痕的对角线长度d;(4)根据载荷F和对角线d计算硬度值,即为试样的超显微硬度值。实验结果表明,超显微硬度与标准显微硬度的偏差大部分在±3%以内,可以有效表征试样的超显微硬度。
本文从硬度的定义出发,寻找更符合接触力学规律以及压痕产生过程的接触面积的最优基准平面。通过微分方法准确获得了接触面积所对应基准平面的位置,寻找到更符合硬度定义的硬度值。基准平面法得到的硬度值的测量误差小于±1.5%,测量稳定性小于1%,该值在理论上比传统对角线方法更接近硬度值的真值,对硬度真值的测量和硬度与其他力学性能的关系的研究具有重大意义。本文以GCr15 钢材料作为试验样品,基准平面法可以准确地测量该样品的微小压痕硬度值。不过,该方法是以压痕边缘凸起为前提,所以理论上仅适用于边缘产生凸起的维氏四棱锥压痕,而对于其他材料的适用结果以及测试效果有待于进一步的研究。
