太赫兹辐射在皮肤中的传输仿真与安全性分析
2021-07-02刘欣缘曾昊旻
刘欣缘,曾昊旻,田 昕,李 松
(武汉大学电子信息学院,湖北武汉430079)
1 引 言
太赫兹辐射(0.1~10 THz)介于红外与毫米波之间,具有通信带宽宽、分子特征光谱明显和对非极性物质穿透性强等特点,因此在高速无线通信、体外疾病诊断、非接触式人体安检等领域表现出了广泛的应用前景[1-6]。特别是低频太赫兹(<1 THz)常用于安检成像系统,目前被动成像安检仪的应用已经比较成熟,但存在成像分辨率有限,受环境温度影响大的问题。随着太赫兹辐射源输出功率和太赫兹探测器灵敏度的不断提升,分辨率更高、信噪比更优、受环境影响小的主动成像式太赫兹安检系统的发展迅速[7-9]。主动式太赫兹成像系统的普及无疑会增加人体暴露在太赫兹辐射之下的风险,也引发了对太赫兹生物安全性的担忧。已有研究表明,高强度的太赫兹辐射能在多种不同尺度上引起生物材料的变化,常见的效应包括结构蛋白损伤、细胞器功能破坏、细胞死亡和组织凝固等。此外,由于生物组织富含的水分子能有效地吸收太赫兹光子的能量并转换为热能,因此太赫兹辐射在生物组织中的热效应也十分显著[10]。
正是由于生物组织对太赫兹辐射的强吸收效应,一般认为太赫兹辐射在穿透衣物后会被人体表层皮肤细胞吸收,而不会对人身安全造成威胁[7]。但这只是一种定性的分析,实际上目前对太赫兹辐射在皮肤中的传输过程与吸收特性还缺乏清晰的认识。Vilagosh 等人使用时域三维电磁仿真软件对太赫兹信号在皮肤中的传播进行了仿真[11],仿真结果表明毛囊能增加太赫兹辐射在皮肤中的传播距离,但频率为0.45 THz 的信号在皮肤中的穿透深度仍小于0.25 mm。Betzalel 等人使用CST 软件对频率为0.4~0.5 THz 的信号在皮肤中的电场分布进行仿真[12],仿真结果表明皮肤中汗腺区域的电场强度较高,有助于促进太赫兹信号在皮肤中的传导。相较于从电磁场角度进行模拟的有限时域差分算法,蒙特卡洛方法从粒子角度对光子在介质中的传播进行数值模拟,具有简单、准确的优点[13-15]。本文建立了皮肤分层结构模型,计算了皮肤中各层组织的复介电常数和光学参数,并通过蒙特卡洛仿真模拟太赫兹辐射在皮肤中的传输过程,进而定量计算了太赫兹辐射在皮肤中由吸收与散射引起的衰减。
2 皮肤组织模型
2.1 皮肤分层结构
人体皮肤组织由表皮、真皮、皮下组织及皮肤附属器构成。综合考虑皮肤的组织结构与电磁特性,在仿真中将皮肤分为4 层,如图1 所示。第一层是去角质的扁平死细胞,厚度约为20 μm,称为角质层。角质层下的棘层与基底层在结构与组成成分上存在比较大的差异,因此又分为两层,其中棘层厚度为30 μm,基底层厚度为50 μm,主要包含脱水细胞、柱状细胞等活细胞以及角质透明蛋白颗粒和黑色素颗粒等[12]。第四层为真皮层,由于皮肤内血管和毛细血管的分布不均匀,真皮层又可细分为乳头状真皮层(厚度约为150 μm),浅表血管层(厚度约为80 μm)、网状真皮层(厚度约为1 500 μm)和深部血管层(厚度约为170 μm),但真皮层整体的折射率、吸收系数等光学参数比较一致,因此在仿真中作为一层来考虑。真皮层下即为皮下脂肪层,这里不作为皮肤的一部分来考虑。
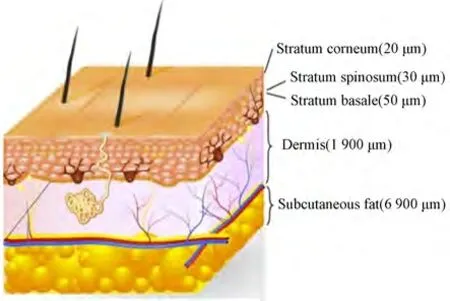
图1 人体皮肤分层结构模型Fig. 1 Human skin layered structure model
2.2 皮肤参数计算
皮肤组织的介电性能由其复介电常数来表示。复介电常数与组织中传输的电磁波频率相关,对于频率在0.1~2 THz 的太赫兹辐射,复介电常数的值可以通过双德拜方程来计算,其中复介电常数的实部和虚部分别表示为:
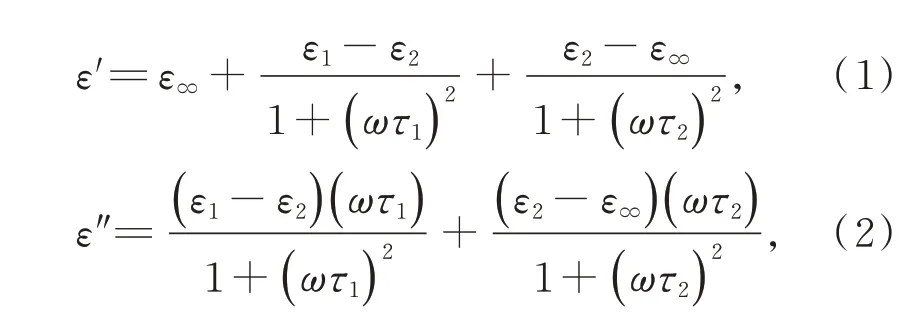
其中:ε∞为高频率极限的介电常数,ε1为静态介电常数,ε2为中间频率极限值,τ1和τ2是松弛时间,下文中将以上参数统称为双德拜系数;ω为角频率。
由于皮肤组织中各层的双德拜系数并不是已知的,本文根据相关论文中给出的太赫兹离散频率的复介电常数和皮肤整体的双德拜系数进行拟合[11,16],得到角质层、棘层、基底层和真皮层的双德拜系数,如表1 所示。
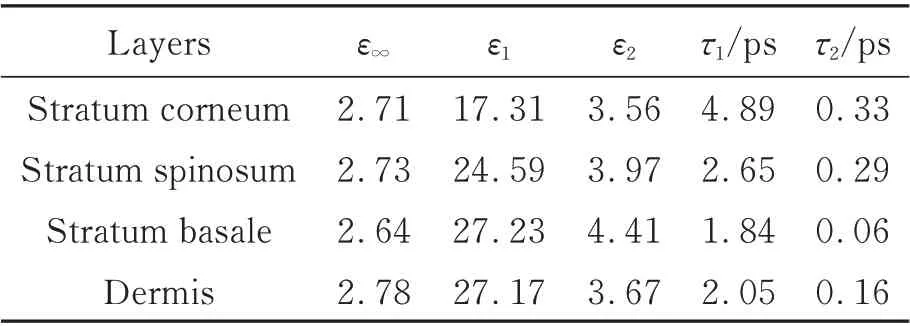
表1 皮肤各层根据离散频率复介电常数[11]的双德拜模型拟合系数Tab.1 Double debye model fitting coefficients of skin layers according to discrete frequency complex permittivity
根据表中的系数,利用式(1)和式(2)可以计算得到皮肤各层在0.1~2 THz 内的复介电常数。图2 中展示了根据拟合的双德拜系数计算的复介电常数与原始数据的对比,从图中可以看出,无论是实部还是虚部,通过离散点拟合得到的双德拜系数所计算得到的复介电常数与原始数据较为吻合,仅在较低频率范围存在误差。将本文中的拟合结果与Truong[17]和E. Pickwell[18]通过实验测量的双德拜系数计算的复介电常数进行对比,如图3~图4 所示。可以看到,由于计算中将皮肤分为4 层,各层的成分不同,而实验中则是将皮肤整体当作一层均匀介质,且Truong取用的是肿瘤附近的皮肤样本,而E.Pickwell 采用的是手腕处的皮肤样本,因此介电常数在数值上略有区别,但基本相当。特别是皮肤角质层的计算结果的实部与虚部都接近E. Pickwell 的实验结果,因此使用这种方法得出的皮肤复介电常数的结果是比较合理的。
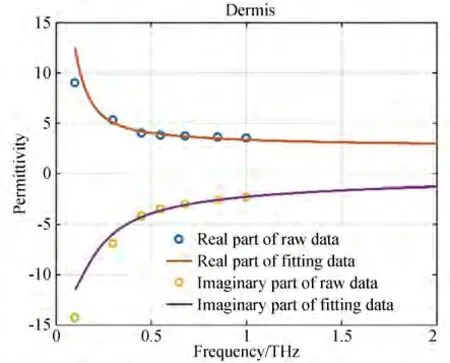
图2 真皮层复介电常数拟合数据与原始离散数据[11]Fig. 2 Fitting data and raw discrete data[11]of complex permittivity of dermis
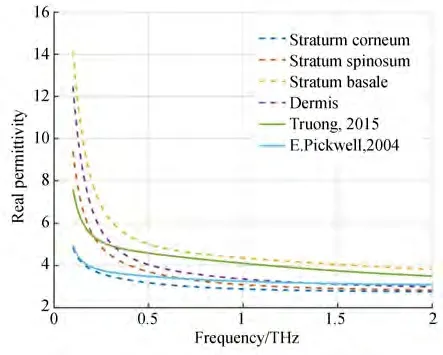
图3 皮肤复介电常数拟合数据与实验数据实部Fig. 3 Real part of fitting data and experimental data of complex permittivity of each skin layer
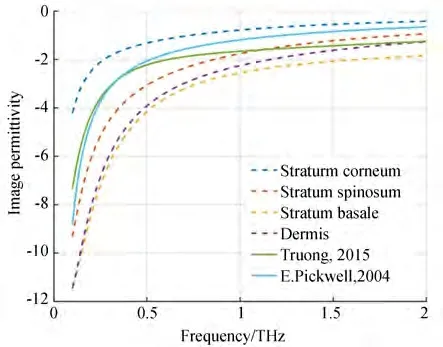
图4 皮肤复介电常数拟合数据与实验数据虚部Fig. 4 Imaginary part of fitting data and experimental data of complex permittivity of each skin layer
通过比较皮肤角质层、棘层、基底层和真皮层的复介电常数可知,无论是实部还是虚部,皮肤各层的复介电常数的数值均随着频率的升高而逐渐下降,其中在0.1~0.4 THz 频段内下降速度较快;而0.4~2 THz 频段内下降速度趋于平缓。在皮肤各层中,角质层的复介电常数最小,而基底层的复介电常数最大,真皮层的复介电常数略大于棘层的复介电常数。
根据复介电常数可以进一步计算皮肤的折射率、吸收系数、散射系数与散射各向异性因子[19-21],结果如图5~图8 所示。其中,皮肤各层的散射各向异性因子均在10-5量级,说明太赫兹辐射在皮肤中的散射可以看作是各向同性的。

图5 皮肤各层的折射率Fig. 5 Refractive index of each skin layer
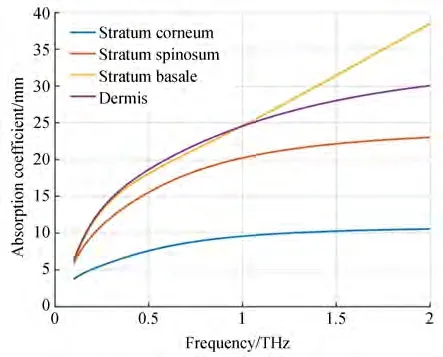
图6 皮肤各层的吸收系数Fig. 6 Absorption coefficient of each skin layer
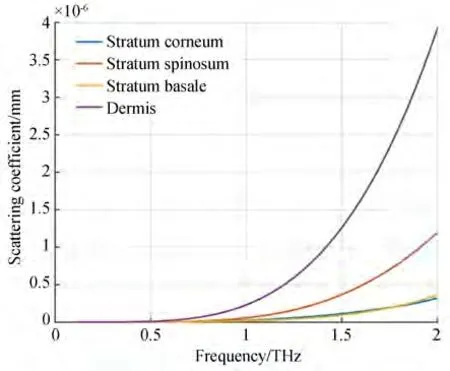
图7 皮肤各层的散射系数Fig. 7 Scattering coefficient of each skin layer
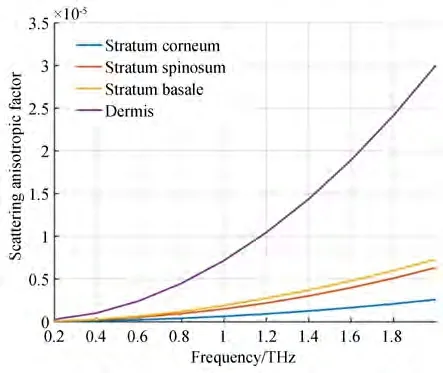
图8 皮肤各层的散射各向异性因子Fig. 8 Scattering anisotropic factor of skin each layer
3 蒙特卡洛仿真
3.1 仿真原理
蒙特卡洛法是一种以概率和统计理论方法为基础的计算方法,使用随机数或更常见的伪随机数来解决很多复杂的计算问题,将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。在某些场合中,传统的经验方法不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡洛法则能够真实地模拟实际物理过程,得到比较准确的结果。而太赫兹辐射在生物组织中的传播就是一个适合用蒙特卡洛法模拟的物理过程[22-24]。
由于生物组织内部散射粒子分布的不确定性,光子在组织中的传播是一个随机迁移的过程,并遵循一定的统计规律。因此,本文采用蒙特卡洛仿真模拟太赫兹光子在介质中的传输。该方法描述了光子传播的局部规则,在最简单的情况下,用概率分布来描述光子在介质体积元素间移动的步长,以及在发生散射事件时光子轨道的偏转角度。三维生物组织模型可分解为若干个体积相同的微小体积元素,每个体积元素的光学参数可以分别设置。当光子在生物组织模型中模拟传播时,需要考虑每一次步长的位移是否离开光子当前所在的体积元素,若离开了当前体积元素进入另一个体积元素,则需要比较两个体积元素的光学参数,考虑路径传播过程中的折射、散射和吸收等相互作用。因此,蒙特卡洛仿真主要考虑生物组织的4 个光学参数:折射率、吸收系数、散射系数和散射各向异性因子,根据这些光学参数可以定量地描述光子的传播过程。
3.2 仿真流程
蒙特卡洛仿真流程如图9 所示,该流程描述了光子从产生到消亡的过程,主要可以分为5 个步骤:
(1)初始化光子的权重w,根据光源类型和方向确定光子的初始传播方向;
(2)根据当前所在体积元素的吸收系数μabs和散射系数μsca,并利用随机数随机产生一个位移步长s:
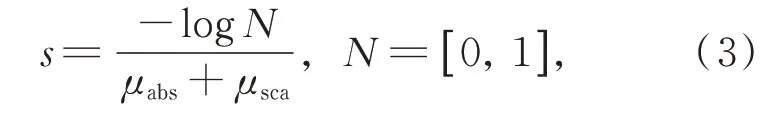
式中N为在[0,1]区间内均匀分布的随机数。
(3)根据传播方向计算当前位置到体积元素边界的距离d,并与位移步长s比较;若d>s,则表明该位移仅在当前的体积元素内进行,因此光子按照该传播方向与传播距离移动,根据当前体元的吸收系数μabs更新光子的权重w=w·exp(-μabs·Δs);若d<s,则表明该位移将穿越当前的体积元素,因此需要先将光子传播至体元边界,根据当前体元的吸收系数μabs更新光子的权重w,将步长s减去位移,并根据相邻体元的光学参数计算新的传播方向;
(4)判断光子的权重w是否小于阈值wth,若小于阈值则代表光子濒临消亡,若大于阈值则返回步骤(2);
(5)生存盘赌是为了避免计算过长的传播路径并且对计算结果的影响较小的情况。当光子权重w下降到阈值以下时,会以1-c的概率终止(通常c<0.1),或以c的概率提升到w/c,因此,所有光子总权重得到很好的保存。
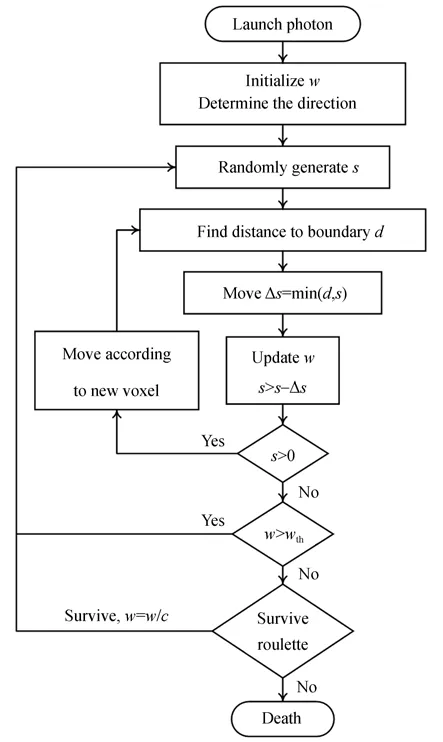
图9 太赫兹光子在皮肤组织中传播的蒙特卡洛仿真流程Fig. 9 Monte Carlo simulation flowchart for transmission progress of terahertz photons in skin
3.3 仿真结果与分析
仿真中模拟的皮肤组织结构如图10 所示(彩图见期刊电子版),使用笛卡尔坐标系进行表示,X-Y平面与皮肤表面重合,Z轴垂直于皮肤表面向下。皮肤各层为平行分层结构,各层的厚度依据皮肤组成模型,图中不同的层组织使用不同的颜色表示,从上至下依次为角质层、棘层、基底层和真皮层。图中的黄色平行直线表示太赫兹辐射垂直入射进入人体皮肤组织,范围为半径50 μm 的圆形区域。皮肤表面的入射辐照度设定为7.16 W/cm2,这是美国空军研究实验室测得的皮肤损伤阈值,皮肤在这种高强度太赫兹辐射下照射2 s 会升温31.72 ℃,并产生不可逆损伤[25]。
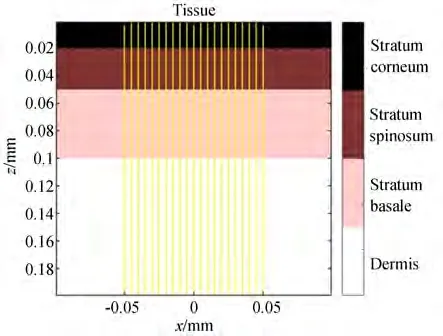
图10 蒙特卡洛仿真皮肤组织结构X-Z 平面图(Y=0)Fig. 10 X-Z plane of simulated skin structure in Monte Carlo simulation(Y=0)
利用上述蒙特卡洛法对0.1~2 THz 之间的太赫兹辐射在皮肤中的传播过程进行仿真,结果如图11 所示。图中绘出了光斑范围内的太赫兹辐射在依次通过皮肤的角质层、棘层与基底层后的平均能量衰减,衰减的能量部分被吸收,部分由于折射和散射的作用改变了传播方向,离开了光斑的中心范围,不足以造成损伤。从图中可以看到,0.1 THz 的太赫兹辐射的穿透性最强,三层总衰减只有-7.3 dB,而2 THz 的太赫兹辐射则衰减了-41.2 dB。因此对于高频太赫兹来说,表面三层总厚度为100 μm 的皮肤组织已经足以吸收大部分的能量,而对于低频段,能量衰减主要是在真皮层中完成的。仿真结果表明,只有0.1 THz 的少部分光子能够进入到皮下脂肪中,如图12 所示,而0.2 THz 以上的光子都无法穿过真皮层继续传播。
从图12 中可以看出,除了强烈的吸收,太赫兹辐射在皮肤中的散射效应也非常明显,大量的光子经过散射改变了传播方向,降低了局部区域的能量密度,也起到了一定的保护作用。在吸收和散射的共同作用下,即使是穿透能力最强的0.1 THz 也很难穿过真皮层继续传播,如图13 所示,皮下脂肪中的光子数比角质层中相差约10 个量级,可以忽略不计。实际上,99.9%的光子的穿透深度都小于0.55 mm,所以即使是很强的太赫兹辐射也很难对真皮层底部造成实质性的伤害。
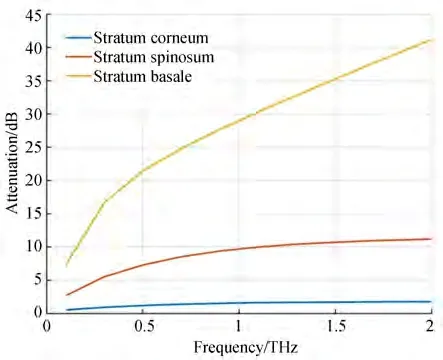
图11 太赫兹辐射经过皮肤各层后的平均能量衰减Fig. 11 Average attenuation of terahertz wave propaqated through different layers of skin
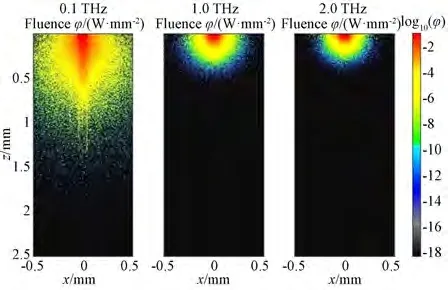
图12 0.1,1.0 和2.0 THz 的太赫兹辐射传输过程的能量分布(X-Z 平面,Y=0)Fig. 12 Energy distribution during transmission progress of 0.1,1.0 and 2.0 THz radiation(X-Z plane,Y=0)
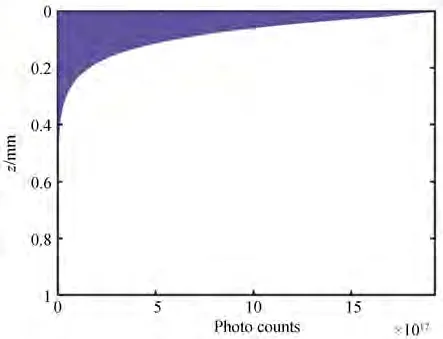
图13 0.1 THz 的光子穿透深度统计图Fig. 13 Statistical graph of penetration depth of 0.1 THz photons
4 结 论
本文建立了皮肤组织的分层模型,通过拟合双德拜系数计算了各层组织在0.1~2 THz 之间的复介电常数和各项光学参数,然后使用蒙特卡洛法计算了太赫兹辐射在人体皮肤组织中的传输过程。仿真结果表明,皮肤组织在对太赫兹辐射有强烈吸收的同时,对组织中的细胞和蛋白质等粒子的散射效应也比较显著,在两者的共同作用下,太赫兹辐射经过皮肤表层的角质层、棘层和基底层时均有明显的衰减,且衰减倍数随着频率的增加而增加。频率较高的太赫兹辐射都会在厚度达到mm 量级的真皮层完全消失,只有穿透性最强的0.1 THz 能有少量光子穿过真皮层达到皮下脂肪,其数量也可以忽略不计。因此,皮肤确实能够保护人体内部免受太赫兹辐射的影响,但由于角质层的衰减作用有限,棘层、基底层和真皮层上部的活性细胞暴露在太赫兹辐射下,仍有引发皮肤病的可能。
