基于Q—学习算法的矿井自适应OFDM调制研究
2021-07-02朱静茹张育芝王安义李萍
朱静茹,张育芝,王安义,李萍
(西安科技大学 通信与信息工程学院, 陕西 西安 710054)
0 引言
煤矿无线通信系统已成为煤矿信息化和安全生产的重要组成部分。与地面无线通信相比,煤矿井下粗糙的巷壁和障碍物会导致煤矿无线通信系统信号幅度大范围波动,造成信号严重衰落,导致煤矿无线通信系统误码率上升,降低了通信质量[1]。因此,如何缓解矿井无线信道衰落对矿井无线通信系统性能的影响是亟需解决的问题。国内外学者针对该问题进行了大量研究,采取自适应OFDM (Orthogonal Frequency Division Multiplexing,正交频分复用)调制技术来对抗衰落,提高频谱利用率,降低误码率。文献[2]将OFDM自适应调制技术应用于井下无线多媒体监测场景来缓解频率选择性衰落带来的影响,提高了井下多媒体传感器网络的可靠性。文献[3]将OFDM自适应调制技术引入井下无线通信系统,解决了煤矿井下多径干扰严重的问题,提高了井下通信的抗噪性和实时性。文献[4]设计了一种能根据信道特征动态改变其比特和功率分配的自适应OFDM算法,提高了井下无线数据传输的抗干扰性。但以上矿井自适应OFDM调制技术均假设信道状态已知,依靠提前确定的固定信噪比门限选择相应的调制方式,调制方式不够智能化,且在实际矿井无线信道中由发送端到达接收端的信号是时变信号,信号传输过程中存在时延,且接收端信噪比估计不是理想估计,导致信号发送端接收到的反馈信道状态与实际信道状态不能完全匹配,造成传统基于固定信噪比门限的自适应OFDM调制系统误码率高及吞吐量低等问题。
Q-学习算法在一定条件下只需采用贪婪策略即可保证收敛,是一种与模型无关的强化学习算法。针对上述问题,本文提出了一种基于Q-学习算法的自适应OFDM调制方法,并将其用于矿井自适应OFDM调制系统。发送端可不用提前已知信道状态信息,在与信道的交互中不断更新状态-动作值函数,最终利用状态-动作值函数学习出动态矿井无线衰落信道下的最佳自适应调制策略,达到降低矿井无线通信系统误码率,提高吞吐量的目的。
1 矿井自适应OFDM调制系统
1.1 系统原理
矿井自适应OFDM调制系统由发送端、矿井无线信道和接收端组成,如图1所示。发送端为矿井下装有传感器的小车,可以在狭长的巷道内自由移动。
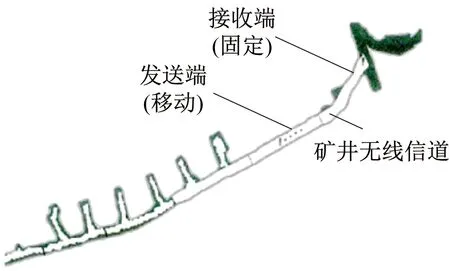
图1 矿井自适应OFDM调制系统组成Fig.1 Composition of mine adaptive OFDM modulation system
矿井小车在移动过程中的自适应调制过程如图2所示。发送端在B1处向接收端发送信道状态信息(Channel State Information,CSI)测试信号,接收端在经过时延后收到CSI测试信号,并对接收到的CSI测试信号进行估计后将结果反馈给发送端,最后发送端移动到B3处,根据接收到的反馈CSI测试信号自适应地分配调制方式。
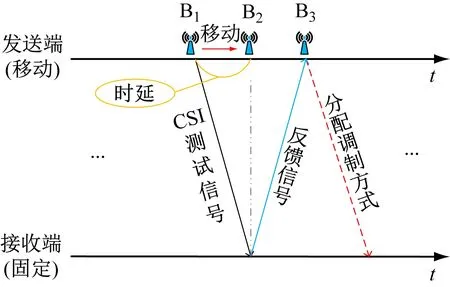
图2 矿井信道自适应OFDM调制过程Fig.2 Adaptive OFDM modulation process of mine channel
1.2 矿井无线信道衰落模型
矿井无线信道易受噪声等外界因素影响,存在衰落现象。一般可将巷道内无线信道衰落分为大尺度衰落和小尺度衰落2种。
1.2.1 巷道内大尺度衰落
巷道内大尺度衰落包括自由空间路径损耗和矿井环境下特定的电磁波传播损耗[5-6]。对于任意距离,特定时间与位置下的路径损耗ζ(t,d)服从正态分布,单位为dB。
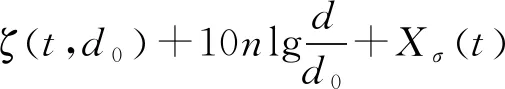
(1)
式中:t为时间;d为信号传输距离;d0为参考距离;n为路径损耗指数,表示路径损耗增长速率;Xσ(t)为阴影衰落,服从均值为0、方差为σ2的正态分布。
矿井巷道中电磁波传播损耗与巷道壁的粗糙度、倾斜度和天线的极化方式等相关,其中垂直极化衰减损耗为
(2)
式中:λ为电磁波信号波长;z为收发天线距离;ω为水平传播方向的半波数;a,b分别为巷道的宽和高;φ1,φ2分别为两侧和顶底板的相对介电常数;ρ为垂直传播方向的半波数。
水平极化波的总损耗为
Ltotal=Lhor+Lrough+Ltile
(3)
式中:Lhor为水平极化损耗;Lrough为粗糙损耗;Ltile为倾斜损耗。
(4)
(5)
(6)
式中:Δh为巷道表面的起伏高度;ϑ为顶壁和巷道壁的倾斜角度。
1.2.2 巷道内小尺度衰落
本文以矿井无线信道普遍采用的Nakagami-m衰落作为巷道内小尺度衰落模型,其概率密度函数[7]为
(7)
式中:r为Nakagami-m包络;m为衰落因子,表征信号衰落强度,m值越大表示信号衰落越小;Γ(·)为Gamma函数;Ω为平均功率。
用Nakagami-m分布能够准确地表征多径信号在复杂场景的衰落情况。采用正弦求和法仿真Nakagami-m衰落信号,将随机序列分解为整数部分和小数部分,Nakagami-m衰落信号为
(8)
式中:α和β分别为调整整数部分和小数部分的参数,β=2m-αp;p为2m的整数部分;g1(t),g2(t)为均值为0、方差相等的2个不相关的实高斯随机过程。
采用多个正弦波的叠加来逼近随机过程g1(t)和g2(t),用等间隔方法来获得多普勒系数和多普勒频率。
(9)
式中:N为正弦波个数;cl为第l个正弦波的幅度;fl为第l个正弦波的频率;θl为第l个正弦波的相位。
(10)
(11)
式中:v为矿井小车运动速度。
1.2.3 矿井无线信道衰落特性分析
发送端天线采用水平极化方式,v=15 km/h,n=2,a=4 m,b=3 m,φ1=φ2=4.5,ω=1,ρ=1,m=1,N=40,d0=1m,Xσ(t)服从均值为0、方差为5的正态分布,Δh服从均值为0.1、方差为0.05的正态分布。基于以上参数对矿井无线信道衰落特性进行分析。矿井无线信道衰落特性如图3所示,蓝色曲线为大尺度衰落和小尺度衰落叠加后的结果,总体呈下降趋势;红色曲线为拟合结果,表征了大尺度衰落的趋势,即收发端距离越远,衰落越严重。
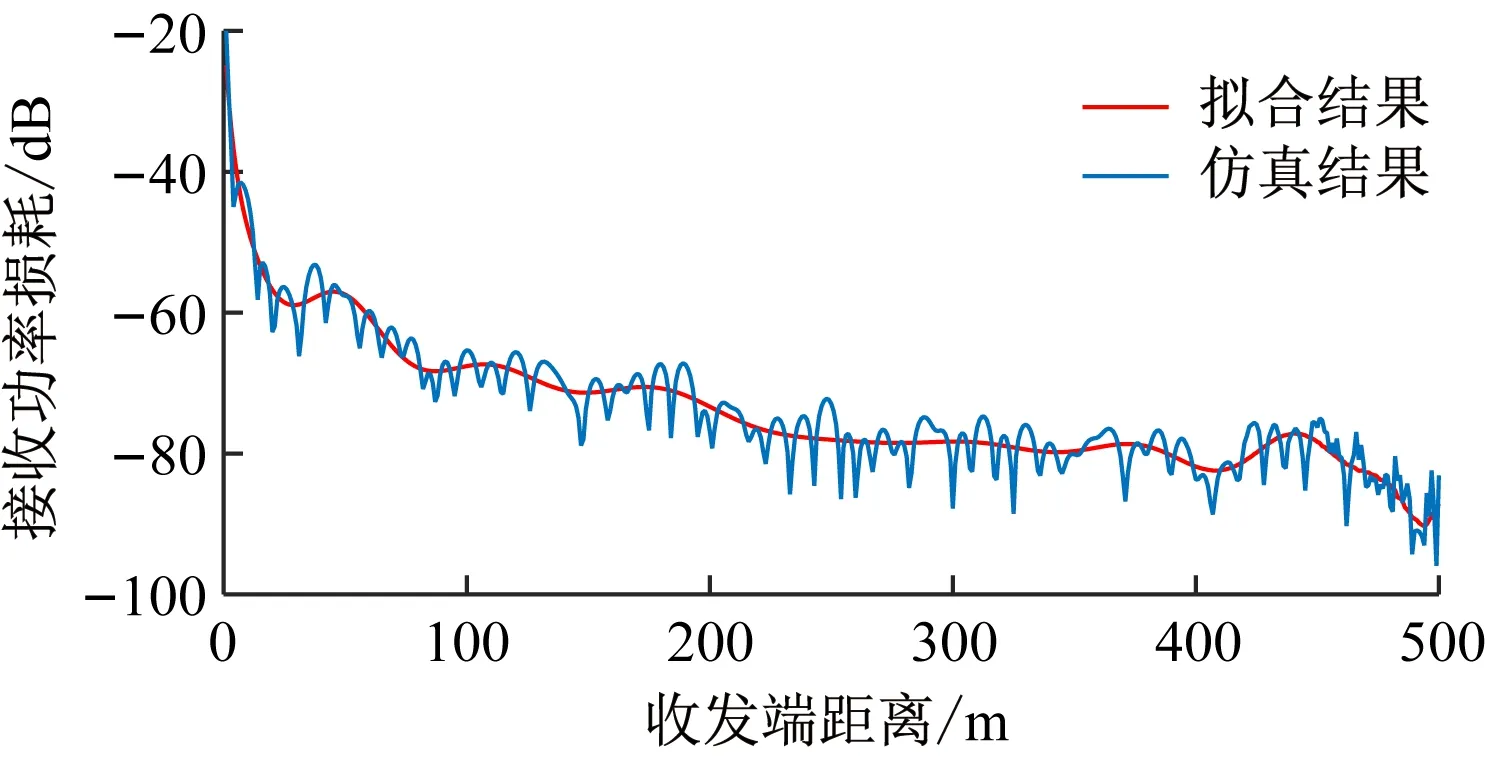
图3 矿井无线信道衰落特性Fig.3 Fading characteristics of mine wireless channel
矿井巷道长且不平整,井下设备多,影响井下移动设备的移动速度,不同移动速度对应不同的衰落程度,因此,本文对2种矿井小车移动情况下的衰落特性进行分析。
(1) 假设矿井小车以15 km/h速度从距发送端100~200 m之间往复移动,总路程为1 km,用时240 s,匀速移动状态下矿井信道衰落特性如图4所示。随着矿井小车往复移动,衰落呈现周期性变化。
(2) 矿井小车从距发送端100~200 m之间往复移动,总路程为1 km,前500 m移动速度为15 km/h,后500 m移动速度变为20 km/h,总用时210 s,矿井小车移动速度变化状态下矿井无线信道衰落特性如图5所示。与图4相比,后500 m的信道衰落更加剧烈,这是因为随着移动速度增大,Nakagami-m衰落更加剧烈。
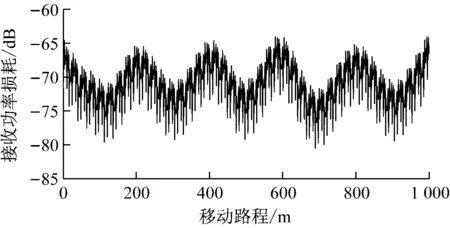
图4 矿井小车匀速移动状态下矿井无线信道衰落特性Fig.4 Fading characteristics of mine wireless channel as mine cart in the uniform movement state
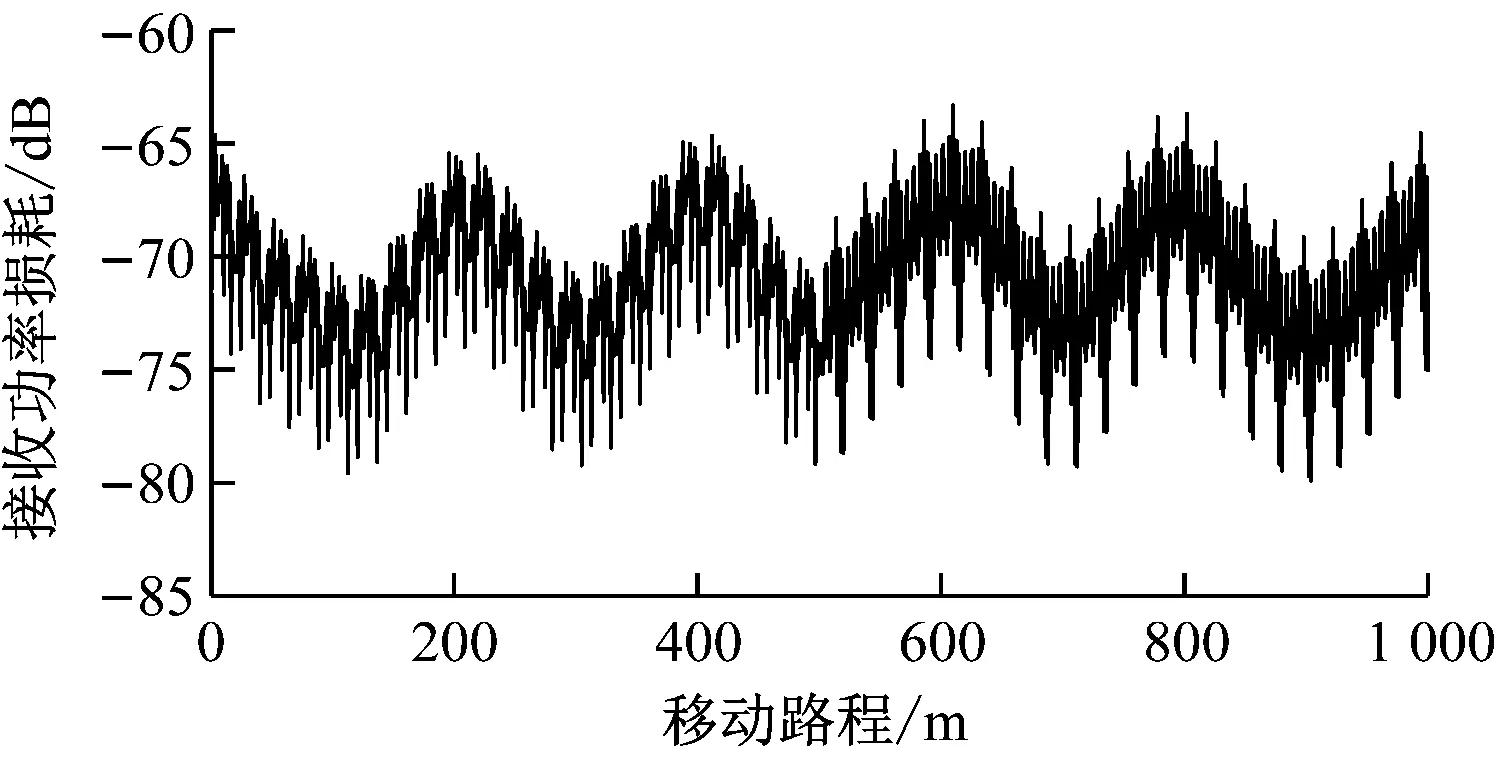
图5 矿井小车移动速度变化下矿井无线信道衰落特性Fig.5 Fading characteristic of mine wireless chamel as mine cart in the non-uniform morement state
2 基于Q-学习算法的自适应OFDM调制方法
2.1 Q-学习算法基本原理
Q-学习算法是Chris Watkins将时间差分与最优控制问题融合后提出的一种强化学习算法,通过对状态-动作值函数进行估计来逼近最优策略。
Q-学习算法框架由智能体、环境、状态、动作和奖励5个要素组成,如图6所示。在每个时刻,智能体都能从环境中接收到一个状态并通过策略产生一个动作与环境继续交互,环境会产生新的状态,同时给出一个奖励,智能体更新状态-动作值函数并进入下一状态。如此循环,智能体与环境不停交互,从而产生更多的数据(状态和奖励),并利用新的数据进一步改善智能体所采取的动作,最终学习相应任务下的最优策略[8-9]。
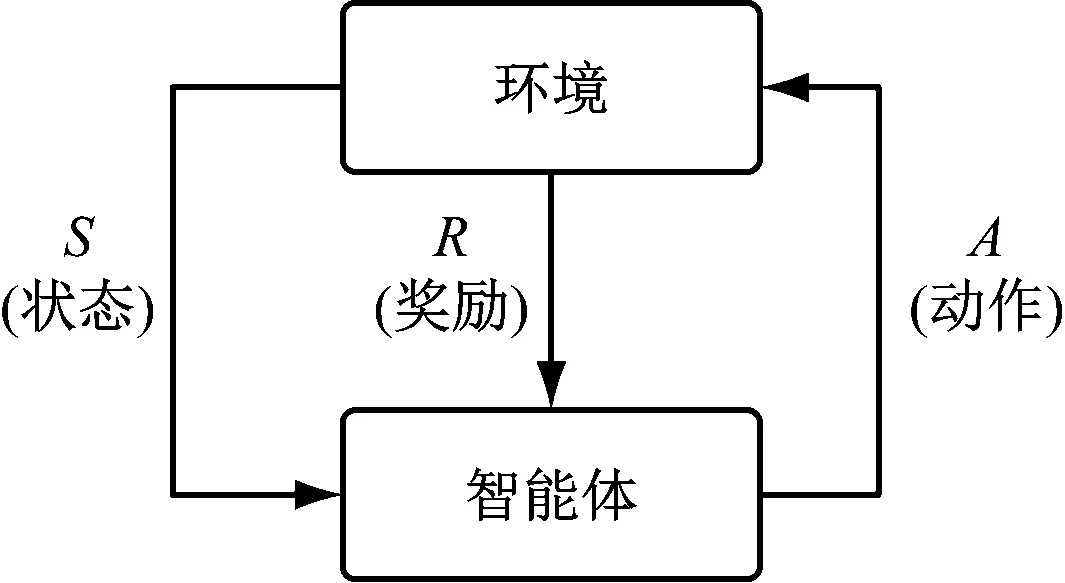
图6 Q-学习算法原理Fig.6 Principle of Q-learning algorithm
Q-学习算法中状态-动作值函数的迭代公式为[10]
Q(S,A)←Q(S,A)+η[R+
γmaxQ(Snext,Anext)-Q(S,A)]
(12)
式中:Q(S,A)为当前时刻的状态-动作值,S为当前时刻的状态,A为当前时刻所采取的动作;η为学习率;R为当前时刻所采取动作得到的奖励;γ为折扣因子;Q(Snext,Anext)为下一时刻的状态-动作值,Snext为下一时刻的状态,Anext为下一时刻所采取的动作。
2.2 基于Q-学习算法的自适应OFDM调制
Q-学习算法中智能体为发送端;环境为矿井无线信道;状态集为矿井小车移动过程中不同时刻收到的反馈状态信息即信噪比(SNR);动作集为OFDM系统下BPSK、4QAM、8QAM、16QAM 4种调制方式;奖励为4种调制方式在不同信噪比条件下的吞吐量。
基于Q-学习算法的矿井自适应OFDM调制根据不断更新的状态-动作值函数,采用贪婪策略来分配调制方式,具体步骤[11-13]为
步骤1:随机初始化Q表(一般为0)。
步骤2:初始化信道状态S,使用贪婪策略根据信道状态S选取一个动作A,即为选取一个调制方式。
步骤3:执行动作A,观测奖励值R和下一个状态Snext。
步骤4:利用式(12)更新Q表。
步骤5:设置下一状态为当前状态,即S=Snext,若S未达到目标状态,则转至步骤3。
根据实际信道状态计算奖励值R,贪婪策略以ε的概率随机选择未知的一个调制方式,避免系统陷入局部最优,1-ε的概率选择当前状态下最大状态-动作值对应的调制方式;状态-动作值更新函数学习率控制连续时刻所能获得状态-动作值之间的差异,折扣因子γ决定下一时刻所获得反馈奖励的大小。因此,合适的贪婪系数ε、学习率η、折扣因子γ是提升整个矿井自适应OFDM调制系统性能的关键。
3 仿真分析
应用Matlab仿真软件,在矿井小车2种移动状态下,对基于Q-学习算法的自适应OFDM调制系统和基于SARSA(State-Action-Reward-State-Action)算法[14-15]、固定信噪比门限的自适应OFDM调制系统的误码率和吞吐量性能进行仿真对比。
仿真环境如图1所示,接收端在矿井巷道入口的固定位置接收CSI信号,发送端处于移动状态下进行信号发送;以4G通信系统为参考,将OFDM系统载波数设为1 024个,采用BPSK、4QAM、8QAM、16QAM 4种调制方式进行自适应OFDM调制。
固定信噪比门限数值从OFDM系统下4种调制方式吞吐量随信噪比变化曲线中得到:当SNR<3 dB时选择BPSK;3 dB≤SNR<8 dB时选择4QAM;8 dB≤SNR<22 dB时选择8QAM;SNR≥22 dB时选择16QAM。Q-学习和SARSA算法中ε=0.1,η=0.9,γ=0.9。
2种移动状态对应的衰落信道信噪比序列为发射功率减去对应的接收功率损耗和加性高斯白噪声后得到的序列。其中发射功率为90 dB,加性高斯白噪声的方差是从7 dB的接收噪声数值计算中得到[16]。
3.1 Q-学习算法参数
在矿井小车匀速移动对应的衰落信道下,仿真ε、η和γ取不同值时对基于Q-学习算法和SARSA算法的自适应OFDM调制系统吞吐量性能的影响,ε、η和γ的取值范围为(0,1),步长为0.1,仿真结果如图7—图9所示。
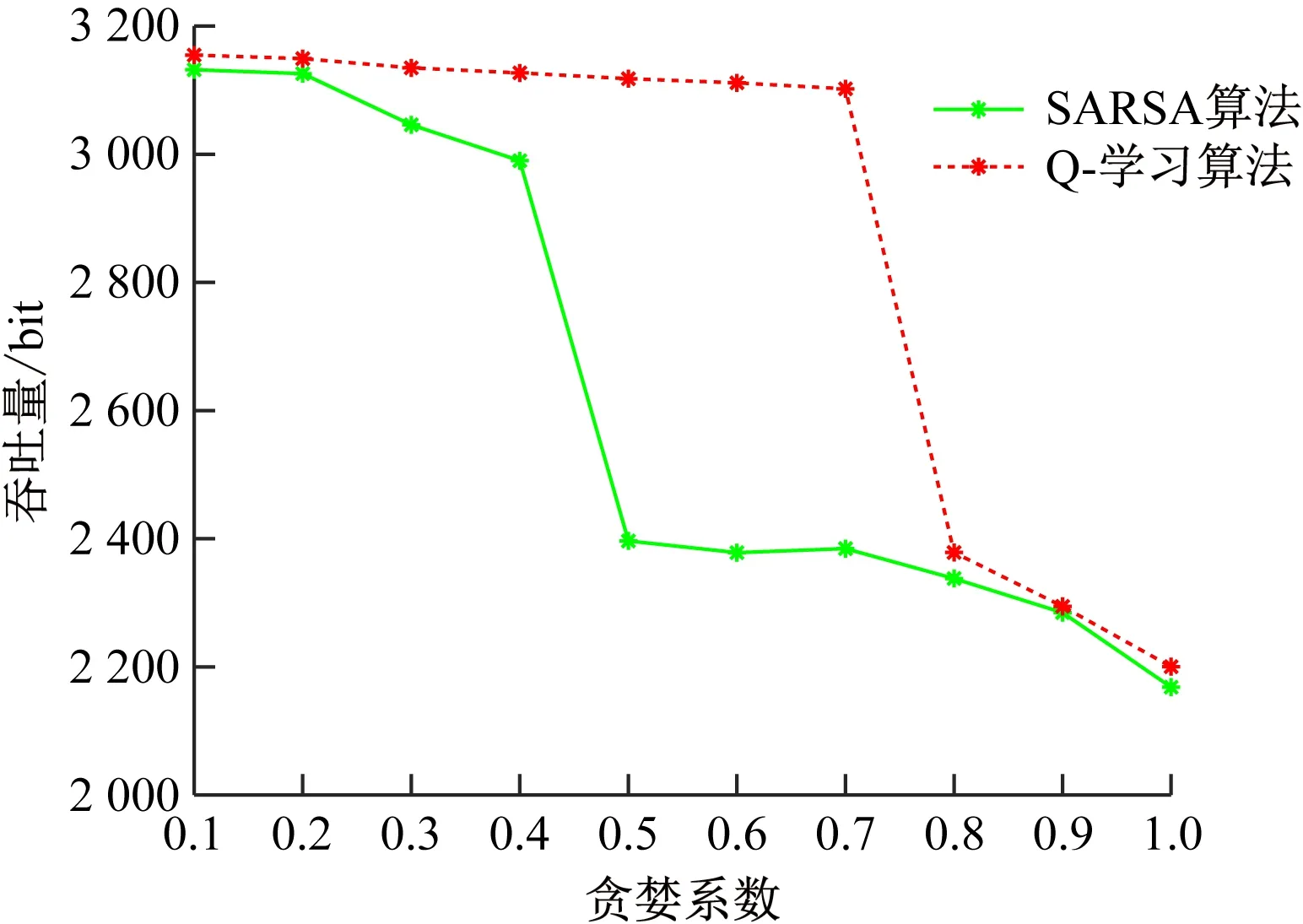
图7 不同贪婪系数ε下的系统吞吐量性能Fig.7 System throughput performance under different ε
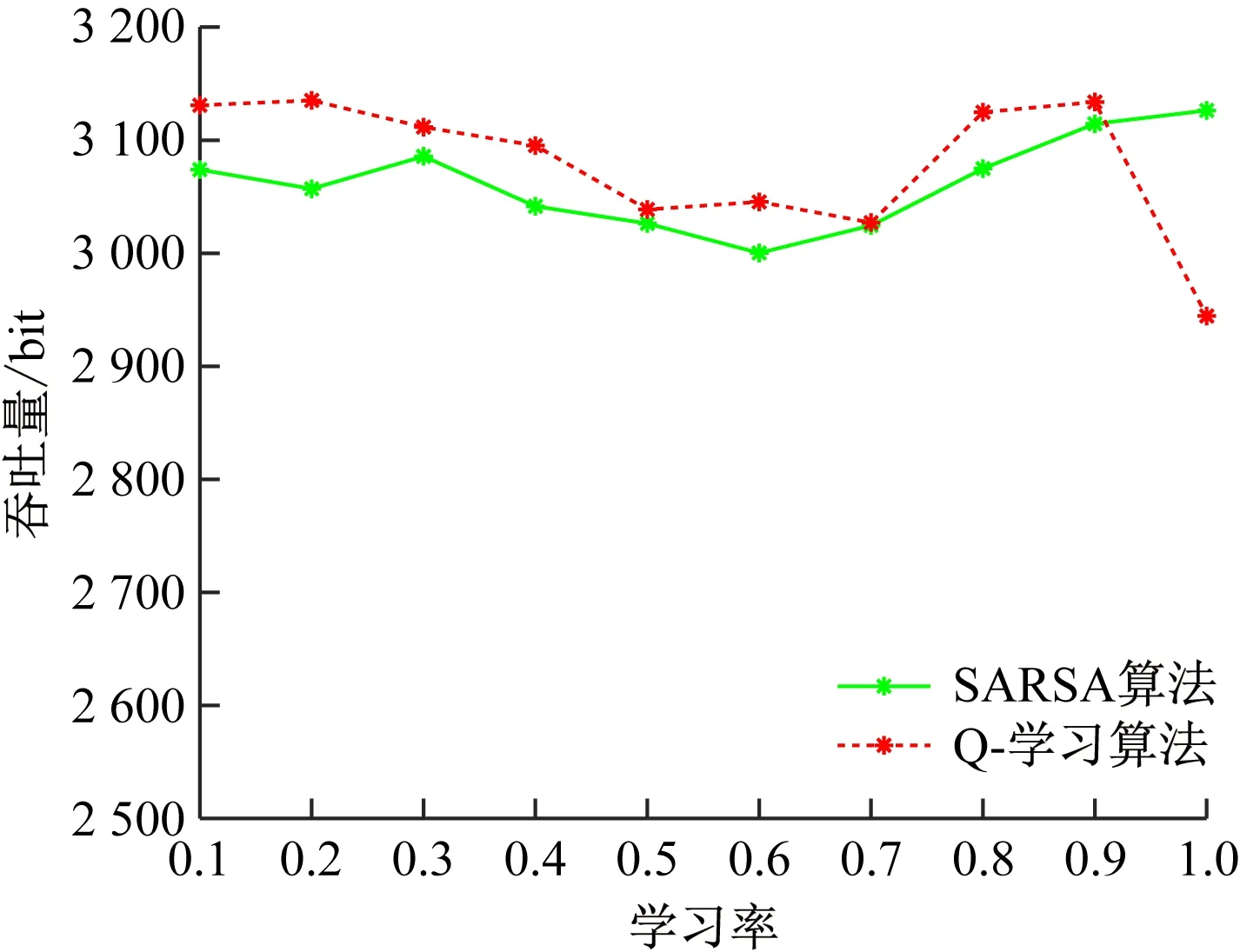
图8 不同学习率η下的系统吞吐量性能Fig.8 System throughput performance under different η
从图7可看出,随着贪婪系数ε的增大,基于Q-学习算法和SARSA算法的矿井自适应OFDM调制系统吞吐量性能逐渐下降,在贪婪系数取0.1时,2种系统吞吐量性能均达到最佳。从图8可看出,在学习率为0.9时,基于Q-学习算法的矿井自适应OFDM调制系统取得最大吞吐量。从图9可看出,在折扣因子取0.9时,基于Q-学习算法和SARSA算法的矿井自适应OFDM调制系统均可获得最大吞吐量。
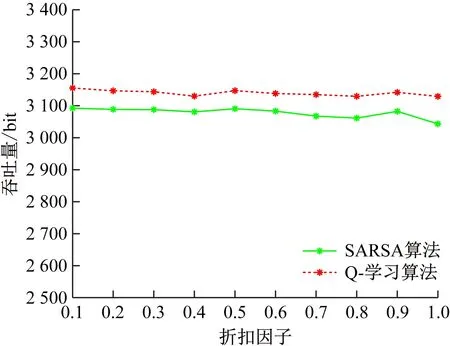
图9 不同折扣因子γ下的系统吞吐量性能Fig.9 System throughput performance under different γ
综上,当ε=0.1,η=0.9,γ=0.9时,基于Q-学习算法和SARSA算法的矿井自适应OFDM调制系统均可获得良好的吞吐量性能。
3.2 仿真结果
3.2.1 矿井小车匀速移动时仿真结果
在矿井小车匀速移动情况下,基于固定信噪比门限、SARSA算法、Q-学习算法的3种自适应OFDM调制系统性能对比如图10所示。
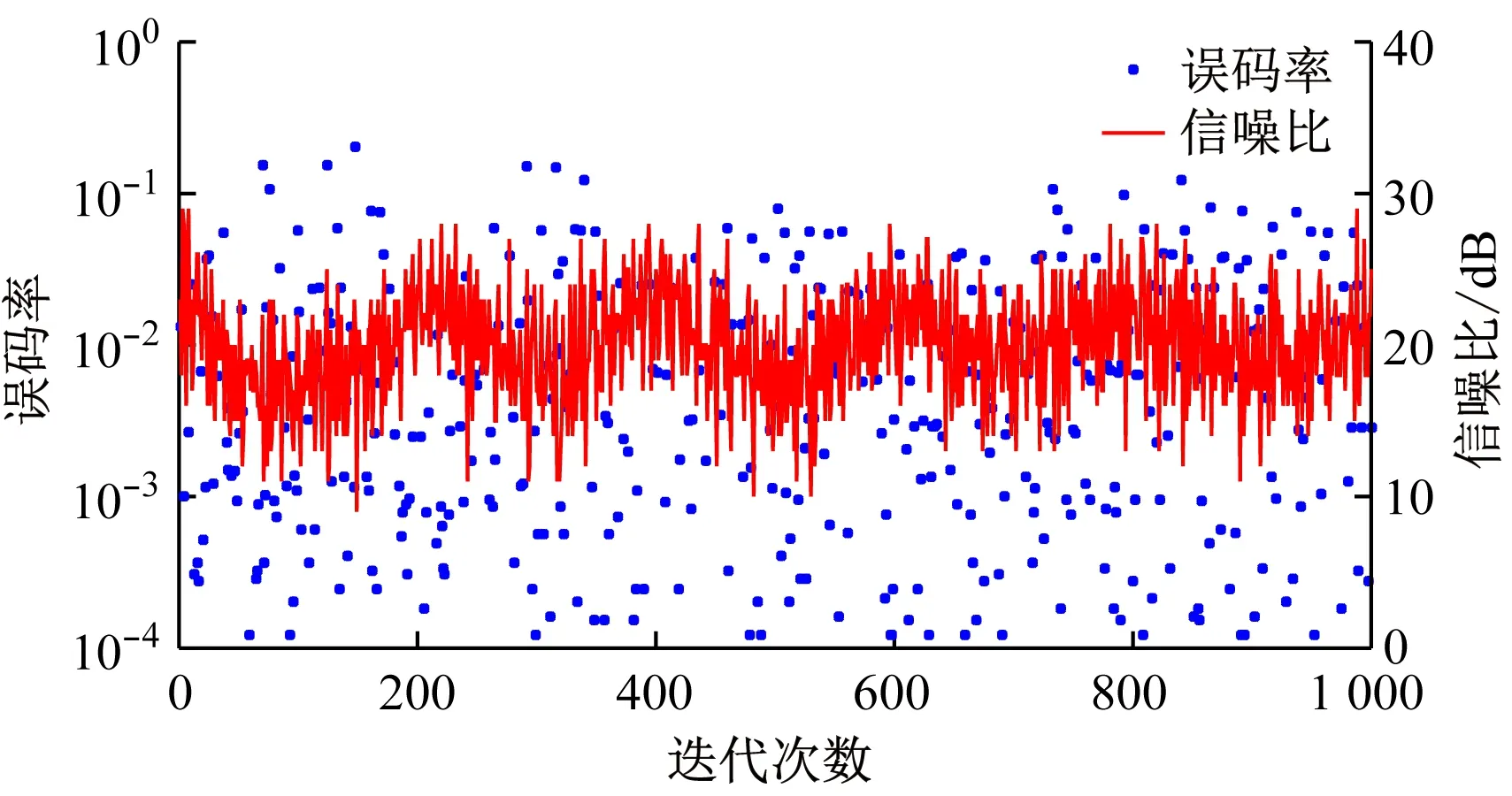
(a) 基于固定信噪比门限的自适应OFDM调制系统性能
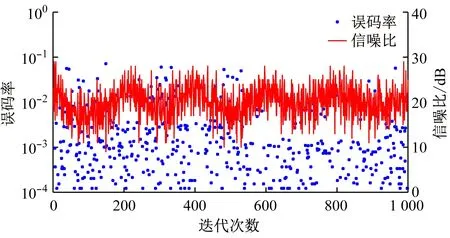
(b) 基于SARSA算法的自适应OFDM调制系统性能
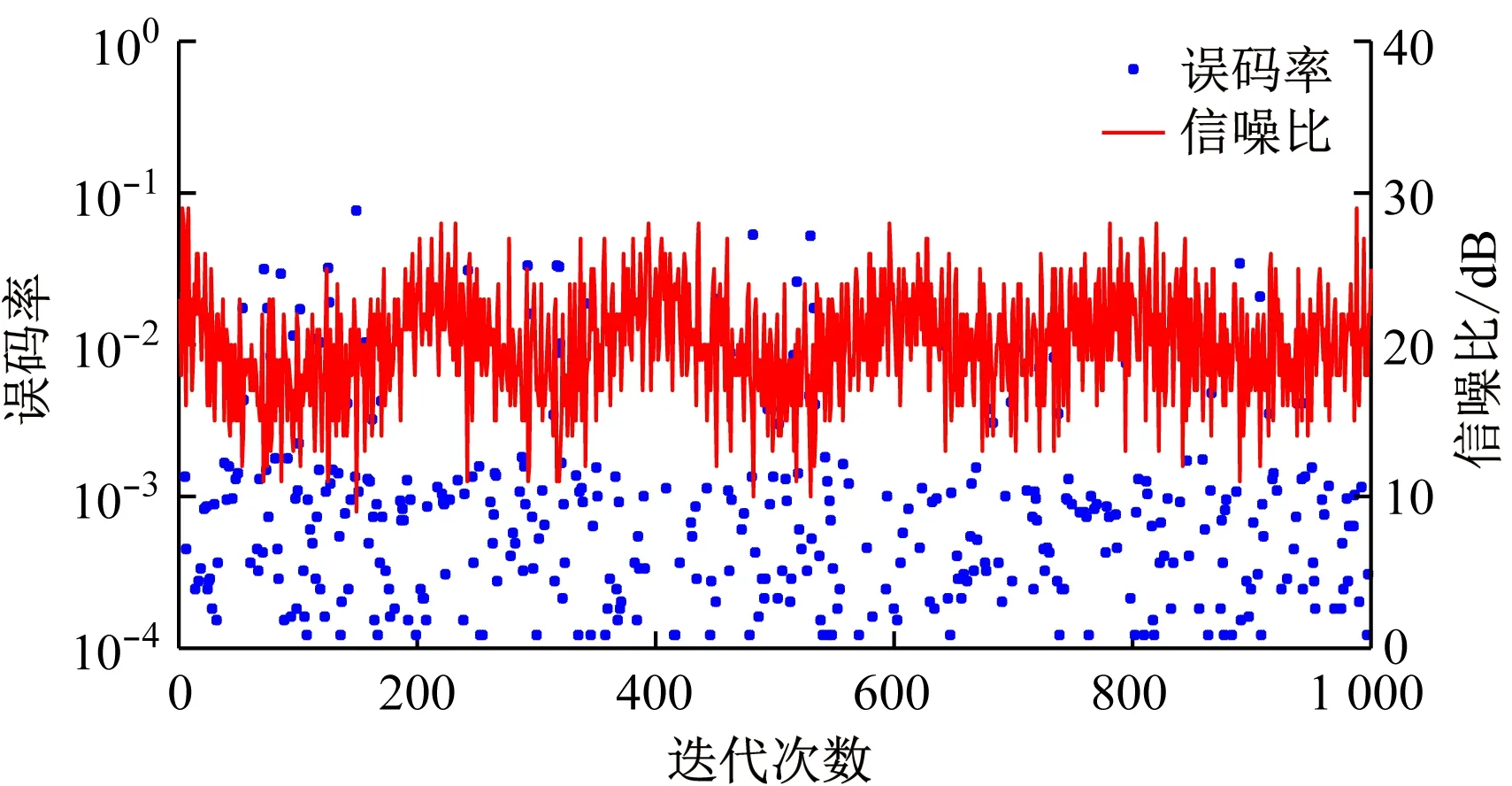
(c) 基于Q-学习算法的自适应OFDM调制系统性能
从图10可看出,在矿井小车匀速运动情况下,基于Q-学习算法的自适应OFDM调制系统的误码率小于基于固定信噪比门限和SARSA算法的自适应OFDM调制系统,且误码率在经过多次迭代学习后下降并最终趋于稳定。
3.3.2 矿井小车移动速度变化时仿真结果
在矿井小车移动速度变化情况下,基于固定信噪比门限、SARSA算法、Q-学习算法的自适应OFDM调制系统性能对比如图11所示。
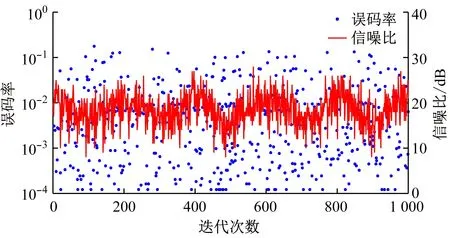
(a) 基于固定信噪比门限的自适应OFDM调制系统性能
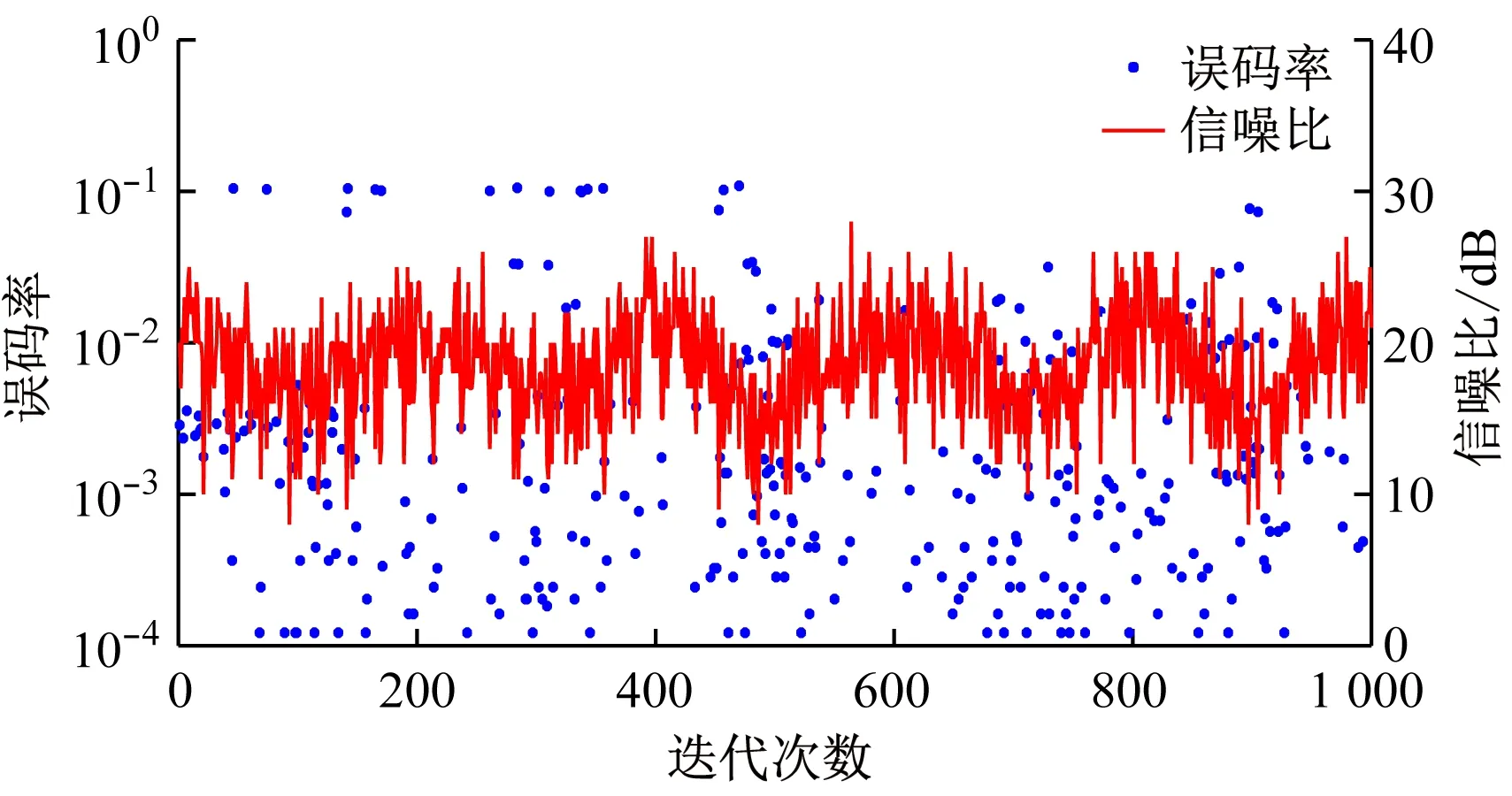
(b) 基于SARSA算法的自适应OFDM调制系统性能
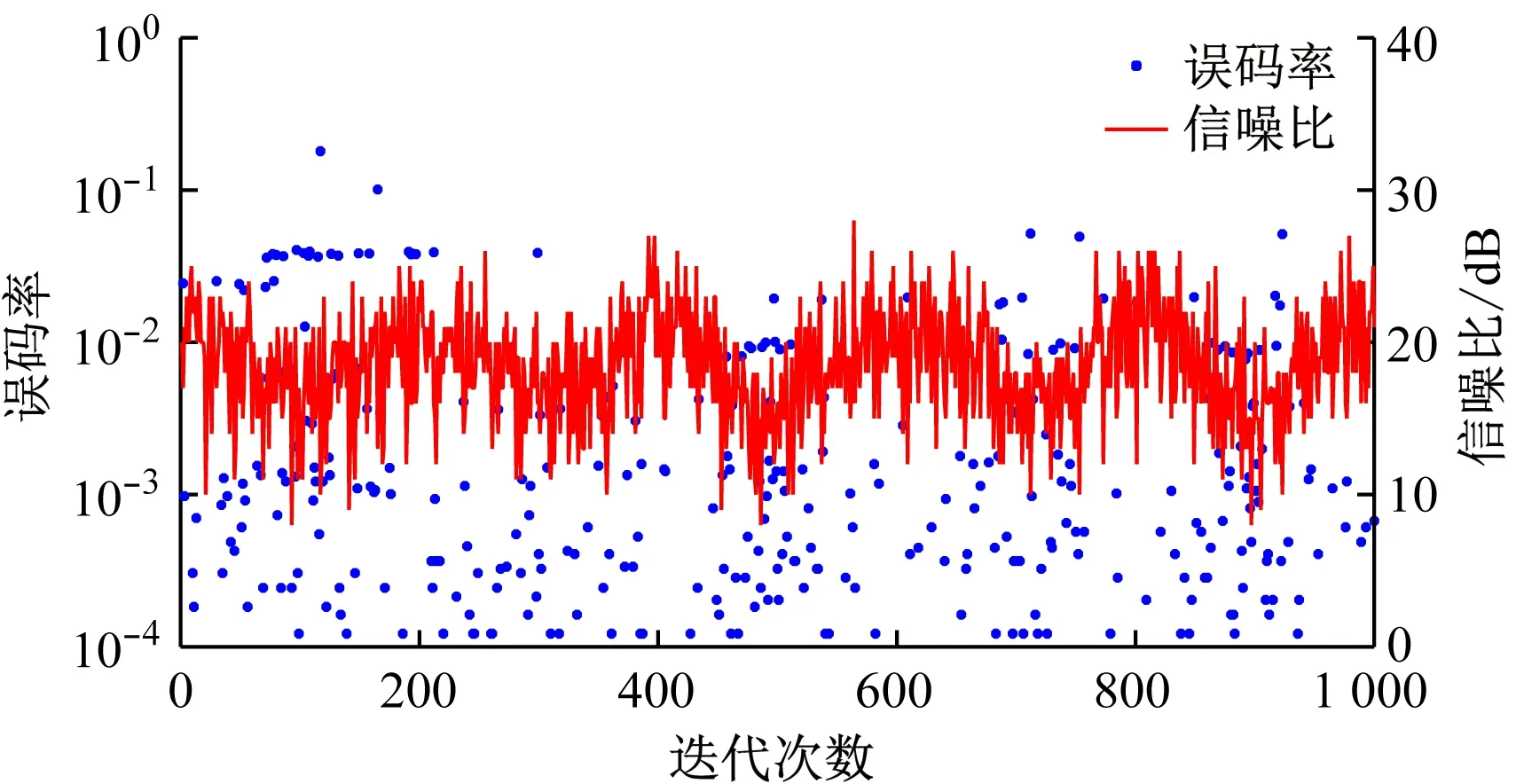
(c) 基于Q-学习算法的自适应OFDM调制系统性能
从图11可看出,在移动速度变化情况下,基于SARSA 算法和基于Q-学习算法的自适应OFDM调制系统误码率明显小于基于固定信噪比门限的自适应OFDM调制系统;基于SARSA算法的自适应OFDM调制系统在经过500次迭代后误码率降低并最终趋于稳定,基于Q-学习算法的自适应OFDM调制系统在经过300次迭代后误码率下降并逐渐趋于稳定,其收敛速度优于SARSA算法。
对矿井小车2种不同移动状态下基于固定信噪比门限、SARSA算法、Q-学习算法的3种自适OFDM调制系统的平均误码率和总吞吐量进行统计,结果见表1。
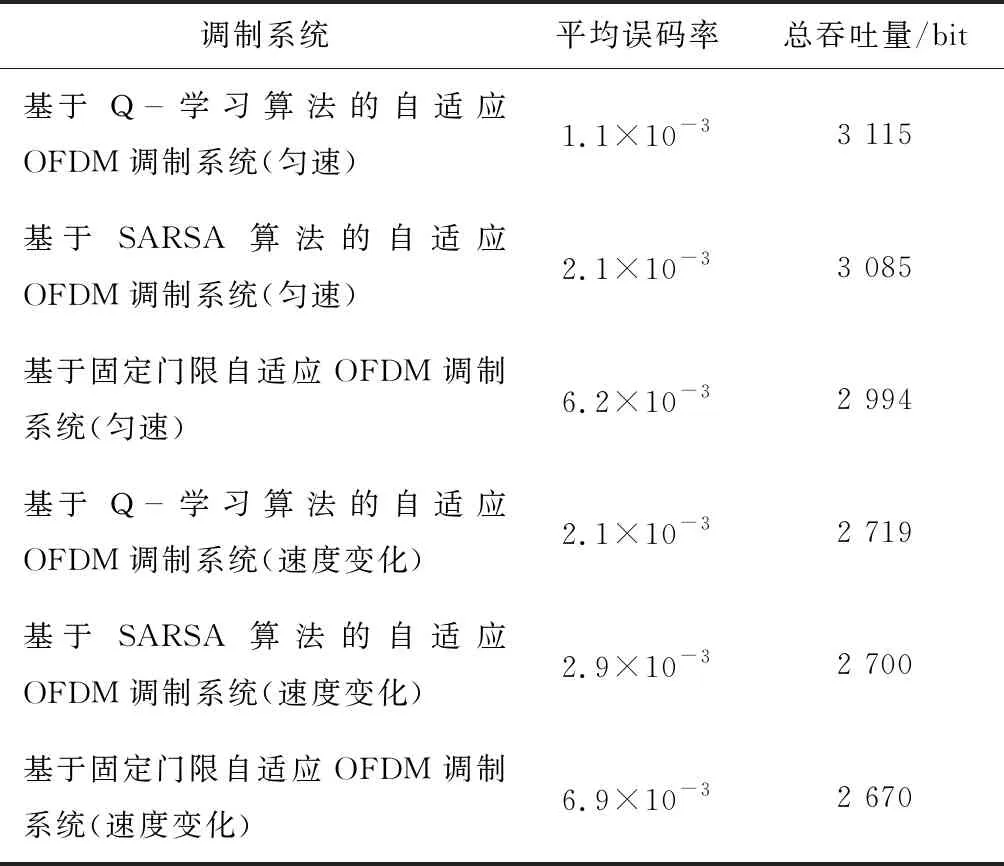
表1 3种自适应OFDM调制系统的平均误码率和总吞吐量Table 1 Average bit error rate and throughput of three adaptive OFDM modulation systems
由表1可知,矿井小车匀速移动状态下基于Q-学习算法的自适应OFDM调制系统平均误码率为1.1×10-3,总吞吐量为3 115 bit,性能最佳;矿井小车移动速度变化情况下基于Q-学习算法的自适应OFDM调制系统平均误码率为2.1×10-3,总吞吐量为2 719 bit,性能最佳。
4 结论
提出了一种基于Q-学习算法的矿井自适应OFDM调制方法,并将其应用于矿井自适应OFDM调制系统。与基于SARSA算法和固定信噪比门限的矿井自适应OFDM调制系统性能进行了仿真对比,仿真结果表明:
(1) 通过优化Q-学习算法中贪婪系数、学习率和折扣因子,可以使基于Q-学习算法的矿井自适应OFDM调制系统吞吐量性能达到最佳。
(2) 矿井小车在匀速和移动速度变化状态下,基于Q-学习算法的自适应OFDM调制系统的平均误码率和总吞吐量均优于基于SARSA算法和固定信噪比门限的自适应OFDM调制系统。
(3) Q-学习和SARSA算法应用于矿井自适应OFDM调制系统时,Q-学习算法收敛速度优于SARSA算法。
