缺陷对EA4T车轴钢疲劳性能的影响

李 行 ，张继旺 ，徐俊生 ，苏凯新 ，张金鑫 ，鲁连涛 ，吴明泽

（1.西南交通大学牵引动力国家重点实验室，四川 成都 610031；2.太原重工轨道交通设备有限公司，山西 太原030032；3.一汽-大众汽车有限公司成都分公司，四川 成都 610100）

车轴是高速动车组走行部关键的承载零部件，其安全可靠性直接关系到列车的安全运行.车轴在服役过程承受来自轨道和车体的各种载荷、腐蚀环境、表面损伤等的挑战，在极端恶劣的条件下会出现由于疲劳断裂引起的失效[1]，而表面损伤是引起车轴疲劳裂纹萌生的主要原因之一[2].近年来，随着中国高速动车组运行里程和速度的提升，车轴在实际服役过程中会出现各种缺陷，无论是材料的加工制造，车轴的装配维修，还是运营中的环境腐蚀或外物冲击，都不可避免地会在车轴表面引入缺陷，这些损伤或缺陷都有可能加速疲劳裂纹的萌生，从而可能导致车轴发生失效断裂.然而，这些损伤不仅会产生应力集中，也会破坏表面涂层，导致车轴锈蚀，进一步降低车轴疲劳性能[2].

从材料、工艺、维修、防护等方面采取措施，高速列车车轴表面仍有可能存在各种损伤缺陷.吴圣川等[3]对高速车轴表面缺陷进行了统计发现，车轴表面主要有划伤、外物损伤等各类缺陷，且这些缺陷都大部分都是具有一定深度和宽度的三维缺陷.目前，国内外就表面损伤对车轴疲劳性能的影响开展了相关研究：吴圣川等[3]采用空气炮装置模拟研究了外物损伤对车轴疲劳强度的影响；周素霞[4]采用线切割方法引入缺陷并从疲劳损伤容限的角度研究了缺陷对空心车轴疲劳性能的影响；高杰维等[5]采用压痕和电火花在车轴钢试样上制造人为缺陷，对比探究了不同的缺口对车轴钢疲劳极限的影响；景启明等[6]研究了环状V形缺口对国产EA4T车轴钢疲劳强度的影响；Beretta等[7]研究了缺陷对车轴钢小试样疲劳强度的影响，并分析探讨了与全比例车轴之间疲劳裂纹扩展的比例效应.

已有的研究结果表明，传统的设计和评价方法已经不适用于损伤车轴的疲劳损伤评估，而应该采用基于疲劳断裂力学的评定方法[3].以往对车轴表面缺陷的研究也都指出了缺陷对材料疲劳强度有降低的作用，并且随着缺陷尺寸的增大疲劳强度下降越明显.然而，从断裂力学的理论出发，建立相应的模型来定量评估表面三维缺陷对车轴疲劳强度影响的研究并不多见.

本文研究对象为用于高速动车组车轴的EA4T合金钢，采用钻孔法在试样表面引入了缺陷，并开展了疲劳试验，研究了不同尺寸缺陷对其疲劳性能的影响，同时基于Neuber公式和断裂力学的方法分别评估了不同缺陷尺寸下的疲劳极限.

1 试验材料和方法

1.1 试样材料和制备

试验采用的材料是EA4T车轴钢（欧洲标准EN13261—2009制造）.车轴热处理工艺为调质处理，表层组织如图1所示，为回火索氏体和贝氏体.由于车轴的疲劳裂纹多从车轴表面萌生，所以本次试验试样均取自实物车轴外表层.车轴合金钢成分组成如表1所示，力学性能为：弹性模量为209 GPa，屈服强度为675 MPa，抗拉强度为791 MPa，延伸率为19%，泊松比v=0.3，硬度为252 HV.

图1 试样显微组织Fig.1 Microstructure of the specimens

表1 EA4T化学成分（质量分数）Tab.1 Chemical compositions of EA4T steel %

将车轴外表层所取材料加工成沙漏形试样，然后使用2000号砂纸打磨去除表面机加工刀痕，并用电解抛光去除表面残余硬化层.将处理好的光滑试样分为两组：一组不做任何处理；另一组用钻孔法在表面人为引入不同尺寸缺陷，带缺陷试样的形状尺寸如图2所示，孔锥角θ为120°.缺陷的等效缺陷尺寸S如式（1）所示[8]，缺陷的具体尺寸如表2.

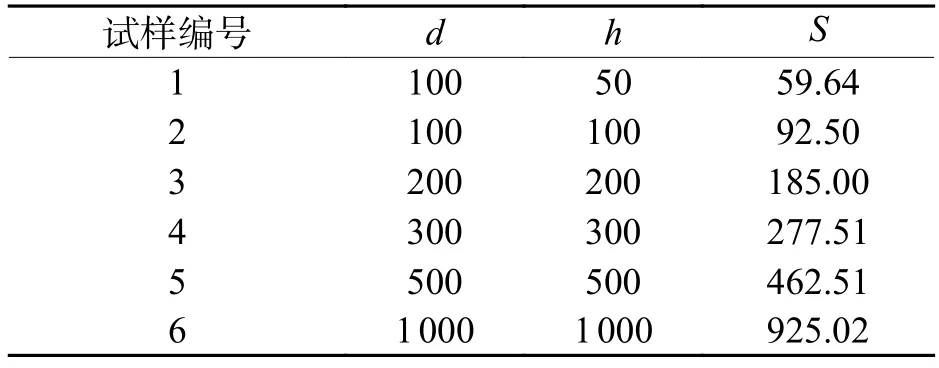
表2 缺陷尺寸Tab.2 Defect size μm

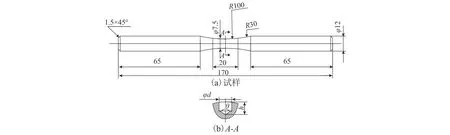
图2 缺陷试样形状及尺寸Fig.2 Shape and dimension of specimen with defect

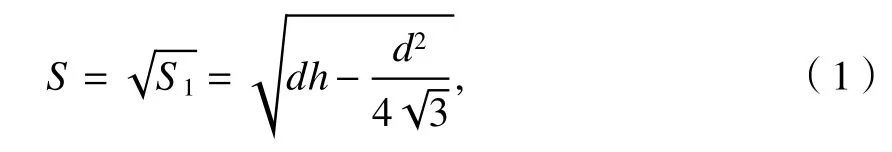
式中：d为钻孔直径；h为钻孔深度；S1为缺陷投影到垂直于最大拉应力的平面上的面积.

1.2 疲劳试验

采用PQ-6型旋转弯曲疲劳试验机开展疲劳试验，频率为50 Hz，应力比为−1，采用升降法，根据GB/T 24176—2009标准，取循环周次为107不发生疲劳失效的加载应力作为疲劳极限.使用JSM-6610LV扫描电子显微镜（SEM）观察所有失效断裂试样的表面以分析疲劳断裂行为.

2 试验结果

2.1 疲劳极限

光滑试样和缺陷试样的疲劳极限（σw）试验结果如表3所示.所有试样在107个循环周次内都具有疲劳极限，光滑试样和试样1的疲劳极限均为360 MPa，其余缺陷试样的疲劳极限均低于光滑试样疲劳极限.由表3可知：存在不会使EA4T车轴钢疲劳极限降低的缺陷尺寸，即当缺陷尺寸足够小时，可以认为该缺陷对疲劳强度没有影响；当缺陷尺寸大于该值时，随着缺陷尺寸的增大，缺陷使EA4T车轴钢的疲劳强度下降，且缺陷尺寸越大，疲劳强度的降低越明显.

表3 不同试样的疲劳极限Tab.3 Fatigue limit of different specimen

试样1的缺陷对疲劳极限没有影响，这是由于疲劳极限不是使裂纹萌生的临界应力，而是使微裂纹不扩展的临界条件.Murakami[8]认为：对于钢材，存在不会降低材料疲劳强度的无损伤缺陷，即当试样缺陷尺寸小于等于无损缺陷大小时，疲劳强度不会降低.对循环加载107周次后不发生失效的试样1的表面进行观察，发现如图3所示的不扩展微裂纹，与Murakami的理论相符合，并且可以推断该缺陷的尺寸小于或等于无损缺陷尺寸.

图3 试样表面不扩展微裂纹Fig.3 Non-propagating crack on the surface of the specimen

2.2 断口观察

光滑试样和试样5断口观察的结果如图4所示.图中：σa为加载应力；Nf为失效时的加载周次.从图4中可以看出：所有试样的疲劳裂纹都萌生于表面或孔附近；光滑试样只存在一个裂纹源，疲劳失效是由晶体滑移变形引起的；对于缺陷试样，由于孔附近存在的应力集中，裂纹从孔周围萌生，在孔底部和表面均存在多个裂纹源.

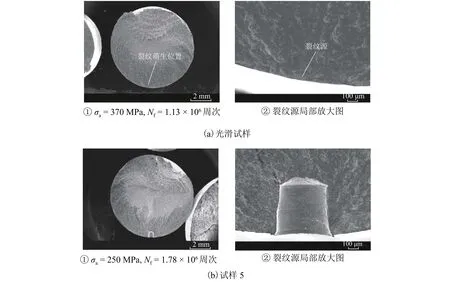
图4 光滑试样疲劳断口观察Fig.4 Fracture surface observations of the smooth specimen

3 讨论与分析

3.1 基于缺口敏感性的疲劳强度预测

利用Peterson[9]提出的缺口敏感性q预测带缺陷试样的疲劳极限，如式（2）.

式中：Kf为缺口疲劳系数，是光滑试样疲劳极限的应力幅σw0与缺陷试样疲劳极限的比值；Kt为应力集中系数，是缺口根部的应力峰值σpeak和没有应力集中时的名义应力σnom之间的比值.

Neuber[10]针对表面没有残余应力，加载应力比为−1时的缺口疲劳提出如式（3）所示的半经验公式.

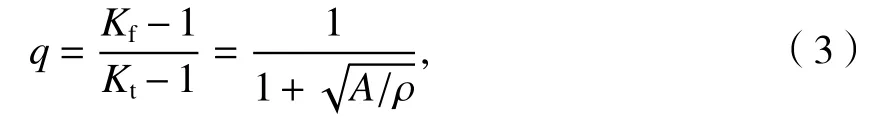
式中：A为Neuber常数，与材料抗拉强度有关；ρ为缺口根部曲率半径.

EA4T的抗拉强度为791 MPa，对应的Neuber常数为0.08[11].将Neuber常数和缺口根部曲率半径代入式（3）求得缺口敏感性，再基于有限元方法求得Kt，由式（2）即可获得Kf，从而预测缺口试样的疲劳极限.

使用ABAQUS软件，根据图2试样尺寸和SEM观察获得的缺陷尺寸建立有限元模型，采用四点弯曲方式加载，如图5（a）所示，其中F为加载力.有限元模型采用C3D4四面体单元，如图5（b）所示，为保证结果精确，模型中部网格尺寸为0.100 mm，孔附近网格尺寸为0.005 mm，其余区域网格尺寸为0.800 mm.

由于试样受到旋转弯曲加载，试样一个循环周次内转动角度不同，缺陷处的应力不同，仿真结果表明：当试样受到的加载力F与Z方向平行时，如图5（c），缺陷处应力最大.基于材料力学的方法计算名义应力，得到不同尺寸缺陷试样的应力集中系数，图5（d）为试样5的孔附近应力集中的仿真结果，其余试样的具体结果如表4所示.

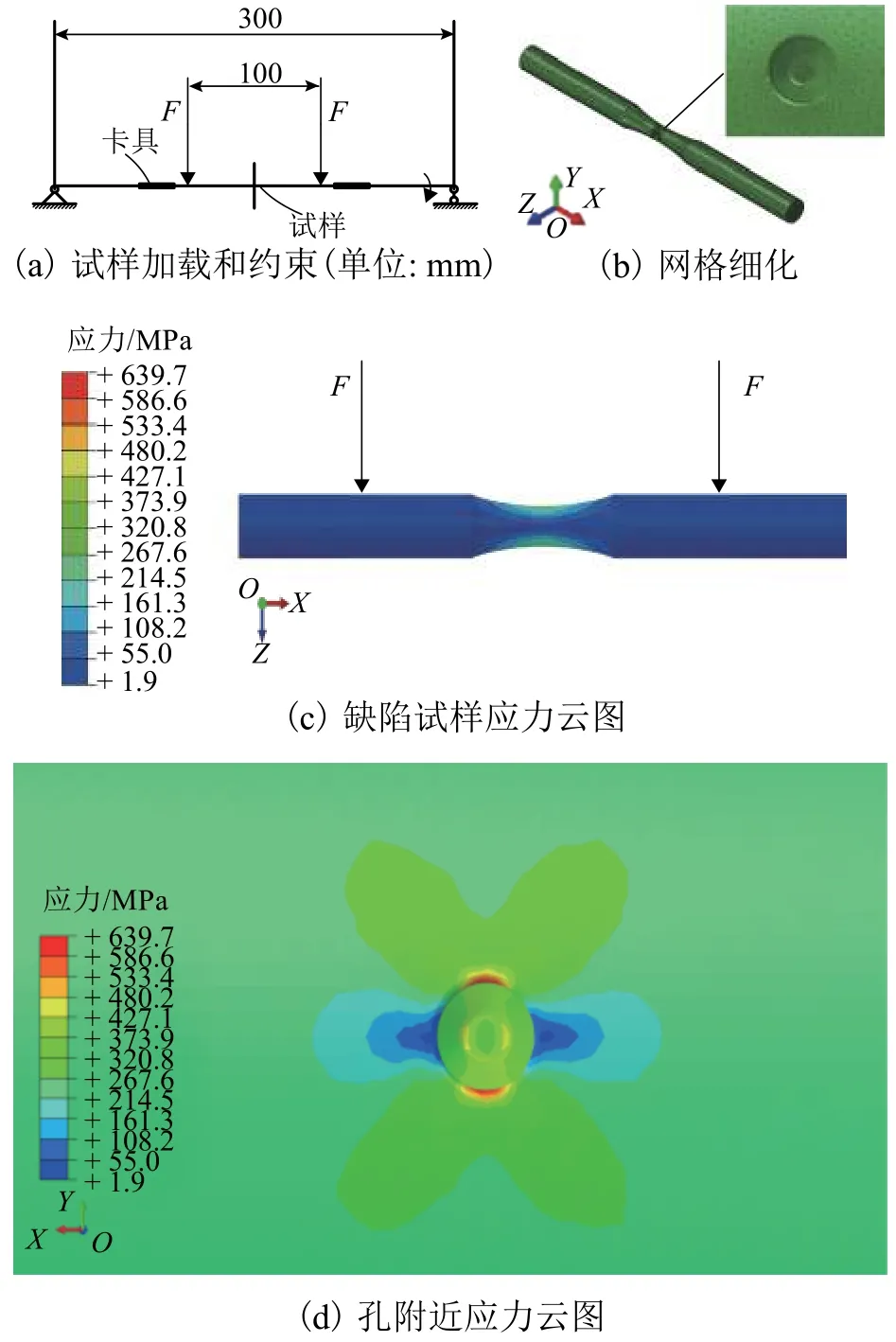
图5 有限元仿真及结果Fig.5 Finite element simulation and results

基于表4 的应力集中系数，结合式（2）、（3），可以预测出不同尺寸缺陷疲劳试样的疲劳极限σest，与试验值进行对比得出相对误差ε，结果如表5所示.由表5可以看出：基于有限元方法，使用Neuber公式预测缺陷试样的疲劳极限具有一定的可行性，虽然估算结果与试验结果偏差较大，但是可以得到较为保守的估算值.

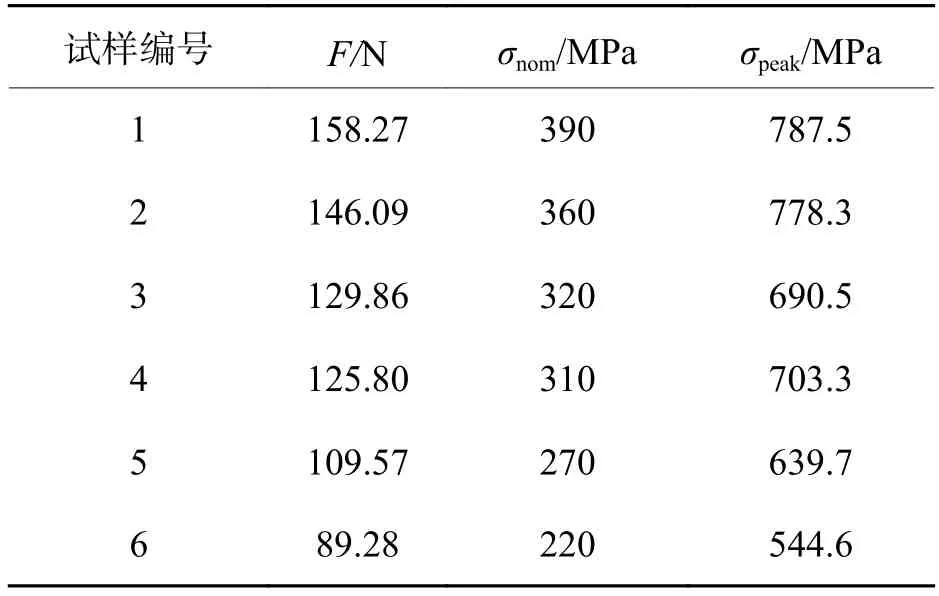
表4 模拟结果Tab.4 Simulated results

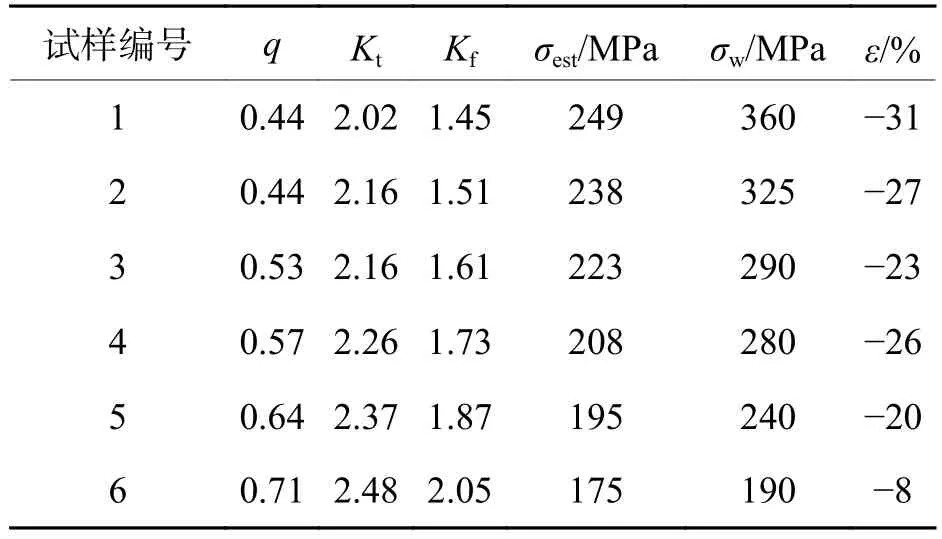
表5 疲劳极限预测结果Tab.5 Result of fatigue limit prediction

分析认为，整体误差较大的原因：一方面可能基于缺口敏感性的理论不能精确评估缺陷试样的疲劳极限；另一方面是由于预测使用的Neuber参数是基于查表法获得，该经验方法也具有一定的误差.需要注意的是试样1与试验误差最大，这是因为此时影响疲劳强度最重要的因素是缺陷尺寸的大小而非应力集中系数Kt[8]，也就是说，实际上Kf=1.00，此时缺陷没有缺口敏感性，基于缺口敏感性的预测方法不适用于此时的疲劳极限预测.

3.2 基于断裂力学的疲劳强度预测

试验的钻孔试样疲劳极限是由不扩展裂纹的临界状态控制的，而且钻孔产生的缺陷可以被视为小裂纹.需要注意的是：对于裂纹长度（或等效长度）小于1 mm的短裂纹，其疲劳裂纹扩展阈值与长裂纹不同，且不是定值，而是取决于缺陷大小和加载应力.因此，为了连续描述短裂纹和长裂纹对材料的影响，El-Haddad 等[12]提出使用应力强度因子（式（4））进行评估，而国内外人员也普遍采用Kitagawa-Takahashi图[13]评估缺陷试样的疲劳强度.

式中：ΔK为应力强度因子范围；a为裂纹长度；Δσ为加载应力范围；a0为El-Haddad常数，与材料有关，如式（5），其中：ΔKth为材料长裂纹扩展门槛值；Δσw0为光滑试样疲劳极限的应力范围.

Murakami[8]利用S参数评估缺陷试样的疲劳极限为

式中：HV为维氏硬度.

另外一种常见的用来评估疲劳极限方法是El-Haddad 模型[12]，如式（7）.

式中：σt为用El-Haddad模型评估裂纹长度为a时对应的疲劳极限.

El-Haddad模型适用于描述无限平面中的二维裂纹，因此准确评估本次试验含孔三维缺陷对疲劳极限的影响，需要对El-Haddad模型进行修正.对于三维裂纹，需要考虑到构件几何形状、缺陷尺寸等影响，因此通过引入三维形状因子α[14]来修正适用于式（4）的裂纹大小，修正后的公式为

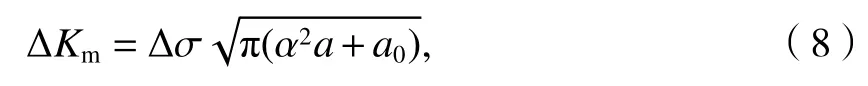
式中：ΔKm为修正后的应力强度因子范围.

令有效缺陷尺寸aeff=α2a，式（8）可以转换为

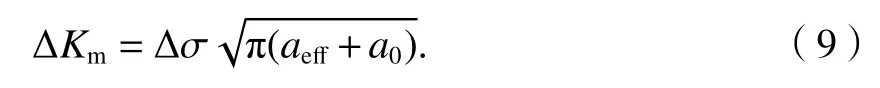
aeff可以用Ⅰ型裂纹的SIF公式表示，如式（10）.

式中：KⅠ是Ⅰ型裂纹应力强度因子；σ是加载应力.

Murakami等[15]认为对于钻孔试样萌生裂纹的KⅠ可以定义为

从而得到α=0.65，aeff=0.42S.

同时由式（8）～（11）可得

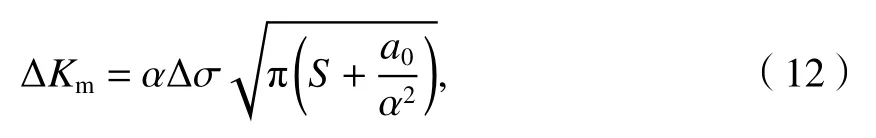
令参数ad=a0/α2，修正后的 El-Haddad 模型为

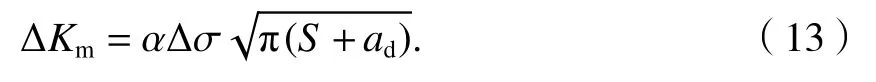
缺口试样疲劳极限σw可以定义为使微裂纹形核但不会持续扩展的临界应力，而门槛值ΔKth可以定义为使裂纹不会产生进一步扩展的阈值SIF，这种临界情况下有

式中：Δσw为缺陷试样的疲劳极限（应力范围）.

对式（13）两边取对数，并且取式（14）的临界情况可得

由于EA4T车轴钢的长裂纹扩展门槛值ΔKth=14.1 MPa[16-18]，将 Murakami公式、El-Haddad 模型和修正后的El-Haddad模型评估结果与试验结果对比，结果如图6所示，其中a0=122.10，ad=290.71.从结果可以看出：Murakami公式和El-Haddad模型都与试验结果有一定的偏差，而修正之后的El-Haddad模型与试验结果误差相对较小，这说明修正后的El-Haddad模型可以更好地预测含孔型缺陷试样的疲劳极限影响.

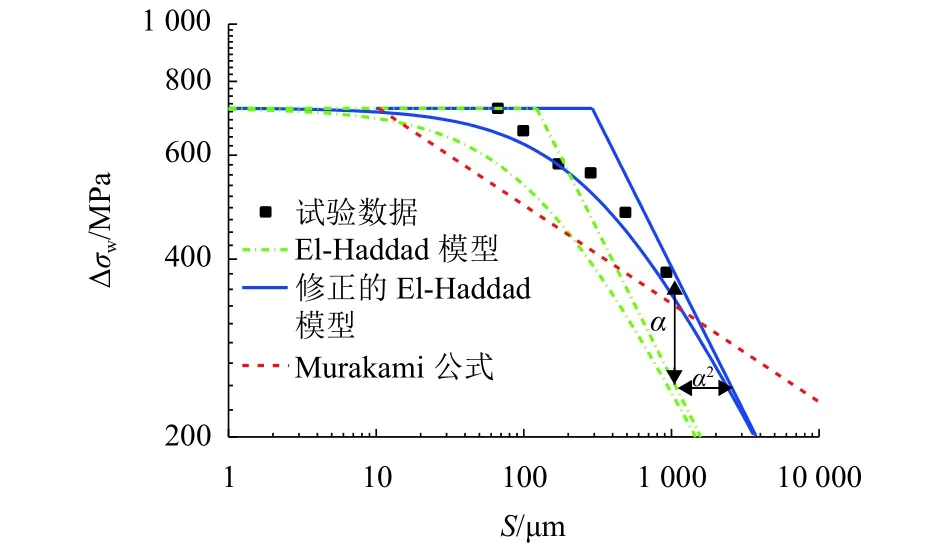
图6 3 种模型与试验结果对比Fig.6 Comparison of three models and experimental results

4 结 论

对EA4T车轴钢光滑试样引入不同尺寸缺陷，开展疲劳试验和疲劳强度评估的研究，得到了以下结论：

1）缺陷尺寸d=100 μm，h=50 μm 时对疲劳强度没有影响，随着缺陷尺寸的增大，缺陷使EA4T车轴钢疲劳强度降低，且缺陷尺寸越大，疲劳极限越低.

2）基于缺口敏感性使用Neuber公式可以预测缺陷试样疲劳极限，虽然有较大偏差，但是预测结果比试验值更为保守.

3）基于断裂力学修正后的El-Haddad模型考虑了三维缺陷的影响，因此与Murakami公式和El-Haddad模型的评估结果相比，能更精确地评估圆孔型三维缺陷对EA4T车轴钢的疲劳强度的影响.

致谢：牵引动力国家重点试验室自主研究课题（2019TPL-T06）.