基于几何约束及迭代的NLOS环境定位算法

邓 平 ，谢 雪

（西南交通大学信息科学与技术学院，四川 成都 610097）

随着5G时代的到来，无线定位技术将成为物联网应用和推广的重要支撑技术.现有无线定位技术中主要包括基于到达时间（time of arrival，TOA）、到达时间差（time difference of arrival，TDOA）、接收信号强度（received signal strength indication，RSSI）、电波到达角度（angle of arrival，AOA）以及 TOA、AOA等多种特征参数的混合定位技术[1]等.在室内、室外等多种5G网络场景的无线定位中，由于移动台（mobile station，MS）能接收到有效信号的基站（base station，BS）数目通常有限，因此在算法设计时通常需要限制可用于定位的BS数量，并考虑用较少数量的BS来实现移动台的位置估计.此外，无论在室内还是室外场景，电波的非视距（non-line-ofsight，NLOS）传播普遍存在，造成 TOA、AOA等电波特征测量值会产生较大偏差，从而大大降低算法的定位精度.

目前，抗NLOS误差定位算法可分为两类：第一类是统计处理法，该方法基于NLOS误差或者信道环境的统计特性进行处理[2-4].例如文献[2-3]使用NLOS 误差和视距（line-of-sight，LOS）误差先验信息，实现LOS重建；文献[4]利用信道环境的先验信息估算NLOS误差大小，实现TDOA测量矩阵和协方差矩阵的重构.但是，由于NLOS误差总是随着环境的改变而动态变化，而实际移动通信环境复杂多变，是很难准确捕捉到所在环境NLOS误差的统计规律，致使这一类算法很难得到有效的工程应用.

第二类算法简称几何法[5-13]，以BS和MS之间的位置几何关系为基础建立约束条件，把求解MS估计位置转换为求解一个最优化问题.这类算法的优点在于可以适应复杂的实际变化环境，有效地利用各种测量信息，但是传统的最优化定位算法往往需要一个比较准确的初始位置估计值才能得到较好的定位精度[6-9].文献[10-12]虽然无需初始位置估计，但该类算法并没有有效利用NLOS传播路径下与被测目标位置密切相关的散射信息.

为此，本文提出一种基于几何约束及迭代的NLOS环境定位算法，考虑在双BS定位的场景下，利用NLOS环境中散射体与BS及MS之间的几何位置关系，并基于圆盘散射模型将最大散射半径作为约束条件构建约束范围.有别于文献[12]的二维网格搜索算法（grid search algorithm，GSA），本文基于一维线性迭代搜索并使用最小二乘估计得到较准确的MS初始估计位置；为了进一步提高定位精度，本文利用阈值处理以及加权平均获得MS的最终估计位置.

1 基于最优化理论的MS定位

在不失一般性的前提下，假设两基站（BS1、BS2）信号在传播过程中都经历了单次散射到达移动台，MS位于△OAB范围内，如图1所示.图中：Rc为小区半径；BS1和BS2分别为主基站和辅助基站；φ 和θ分别为BS1测量的和真实的AOA值；ri为MS到 BSi的真实 TOA 距离，i=1，2；Si为BSi到 MS 的信号散射体.

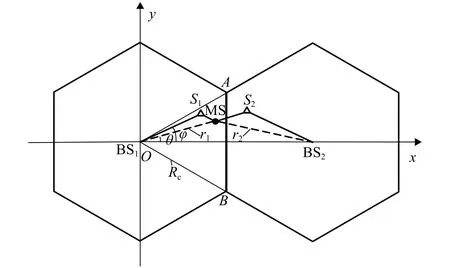
图1 基站与移动台位置关系Fig.1 Location relationship between BS and MS

设MS位置坐标为(x,y)，B Si坐标为(xi,yi),则有

在单次散射模型下，散射点Si坐标为(xSi,ySi)，MS 到B Si的测量距离为Ri，ηi为其测量误差，µ 为BS1测量的AOA误差，由此建立测量等式如式（3）和式（4）所示.

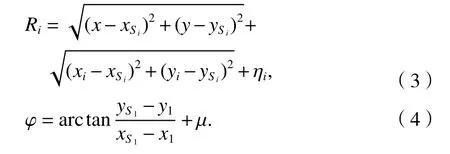
由于在NLOS环境中信号无论被折射或者反射都会使得测量值大于真实值，因此存在NLOS因子αj(j=1,2,3)满足：

类似于文献[1]的混合线性定位（hybrid line of position，HLOP）算法，联合式（1）、（2）、（5）、（6）可得有关αj的方程组：

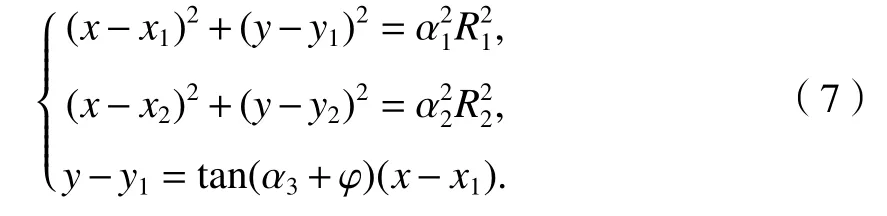
式中：

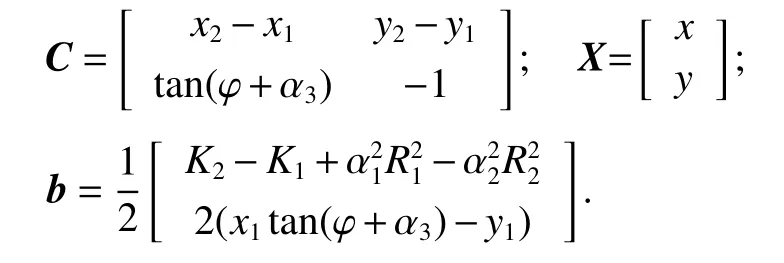
那么 MS 位置估计值可通过 LS（least squares）求解，即

由式（9）可见，MS定位精度关键取决于是否能获得准确的αj取值，而传统最优化处理方法通常根据MS和BS之间几何位置关系将该问题转化为非线性约束最优化问题进行求解[6].

如上所述，进一步建立非线性约束最优化模型.首先由图1中BS和MS的三角关系建立不等式约束，并联立式（5）表示为矩阵形式，如式（10）.

接着，基于文献[6]参量取值约束思想，以及蜂窝半径Rc约束，可以获得关于α1、α2的上、下界关系，如式（11）.

考虑MS真实位置始终位于△OAB可行域内，可得B S1的两条AOA位置线范围，如式（12）.

式（11）和式（12）中：αj,upp、αj,low分别为αj的上、下界.

为了减小测量误差的影响，这里以测量值与目标值的残差平方和为非线性目标代价函数，如式（13）.

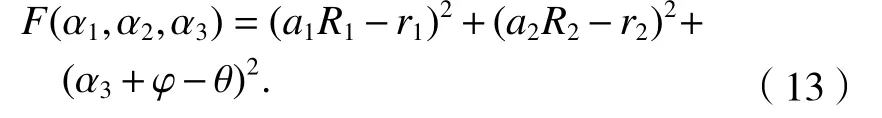
此外，MS位置坐标存在对应的几何位置关系，如式（14）.

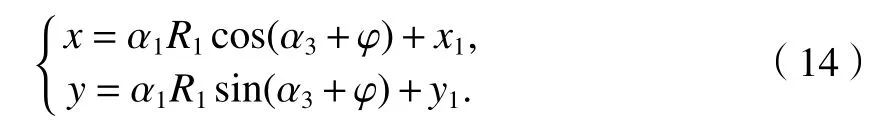
因此，将式（1）、（2）、（14）代入式（13）可得新的代价函数，如式（15）.

综上，αj求解问题演化为式（16）非线性优化问题：

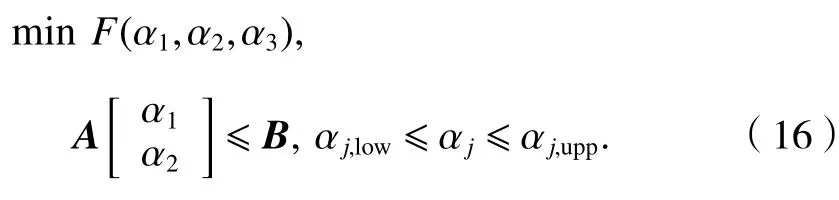
求解式（16）常用的方法是内点法，其思想是利用约束条件和目标函数来构造罚函数，将不等式优化问题转化为无约束优化问题，然后给定初始值线性逼近目标最优解[14].不失一般性，仿真中变量αj初始取值为αj=(αj,low+αj,upp)/2，随后使用MATLAB优化工具箱对优化问题进行求解.在获得αj的最优解后，将其代入式（9）即可得到MS的估计位置.

2 基于散射信息约束及迭代的定位算法

上述定位过程的关键是如何求解准确有效的αj值.由于传统最优化求解方法很难确定一个有效的初始变量值使得算法尽可能收敛，且很有可能出现局部最优的情况，本文提出充分利用NLOS环境中的散射信息缩小MS可行域，并以线性迭代方式在αj可行域内搜索满足约束条件的αj值.

2.1 散射半径几何约束条件

为了减小目标搜索范围，本文考虑在单次圆盘散射模型[15]下引入最大散射半径作为约束条件，其中BS和MS与散射体（图中用△表示）的几何位置关系如图2所示.

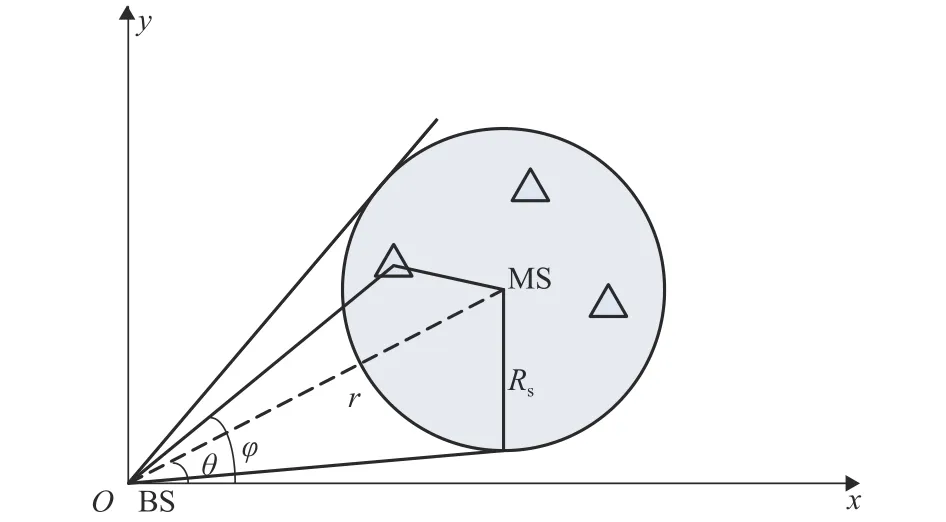
图2 基站、移动台和散射体的几何关系Fig.2 Geometric relationship of BS，MS and scatterer

假设最大散射半径为Rs，由图2三角形三边关系可得BS到MS真实距离r大于最大散射半径，即

那么，将式（5）中测量值与真实值对应关系代入式（17），可得有关α1、α2的约束不等式如式（18）.

如果忽略AOA测量误差，从图2几何模型可知α3的最大值为

类似地，把式（5）、（6）代入式（19）可以获取有关α1、α3的约束不等式为

最终，在散射半径约束下，有关NLOS因子αj新的约束条件为

2.2 基于迭代的MS位置估计

对于以上非线性约束模型，可以基于内点法求解，此外还可以使用文献[13]的网格搜索算法，通过二维网格搜索αj并结合最小二乘的方式计算得到MS可能位置点，再对其算术平均可得到MS估计值.但是网格划分密度极大地影响网格搜索计算量以及定位性能.为此，本文通过一种线性迭代法以αj为权值进行一维全局搜索，随后LS估计出MS初始估计值；为了进一步抑制较大的NLOS误差，本文提出利用MS初始估计值与主基站B S1的距离平均值作为阈值，从而筛选出MS所有可能位置点，最后进行归一化加权得到MS最终估计位置.

因此，将所提出算法在有散射半径约束（约束条件为式（21））下的主要步骤描述如下：

步骤 1首先确定搜索步长l1和l2.将α1、α2区间长度划分成k等份，作为迭代增量，如式（22）.

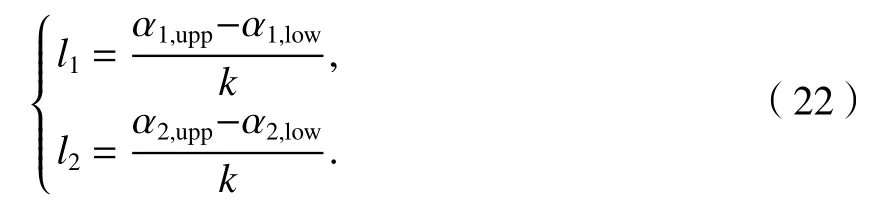
步骤 2设置下一时刻迭代因子 α1、α2.这里选取 α1、α2的迭代初始起点为α1,0=α1,low,α2,0=α2,low，将满足约束式（21）的 α1、α2代入式（23）计算相应 α3，并判断 α3是否满足约束条件式（21），若满足则继续执行步骤3，否则进行下一次迭代, 设置下次迭代参量为α1=a1,0+l1, α2=a2,0+l2.

步骤3获取MS的一个估计位置.将步骤2中搜索的有效αj代入式（9），从而计算出MS的一个初始估计位置(xcp,ycp).

步骤4MS估计位置点筛选.在NLOS环境下，所有MS可能位置点均应在观测基站的定位圆内，这里考虑将MS可能位置限制在以B S1为圆心，Dthr为半径的圆内，其中Dthr表示MS所有初始估计值与BS1的距离平均值.假定通过迭代计算有N个MS 初始估计位置点(xcpn,ycpn),n=1,2,···,N, 则Dthr可表示为

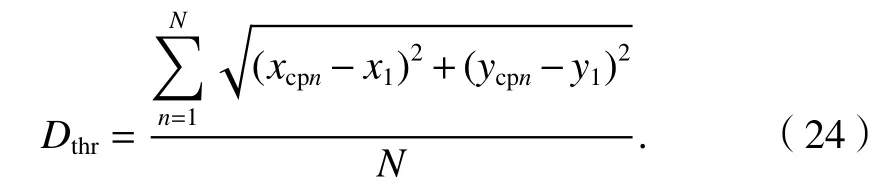
步骤5计算MS加权估计位置.假定阈值筛选出M个MS候选位置点，其位置坐标为m=1,2,···,M，平均位置坐标为，则各候选点与之距离为利用 的dm归一化倒数作为加权系数，即可得到MS的最终位置(xMS,yMS).

算法在无散射半径约束下的处理过程类似，只需将步骤2中的约束条件替换为式（10）～（12）即可.

3 算法仿真与分析

图1蜂 窝 网络 环境 中 ，假 定Rc为1000 m，MS 坐标为(7 00,100)m，BS1、BS2坐标分别为(0 ,0)、散射体由给定散射半径的单次圆盘（disk of scatter，DOS）模型产生，TOA 距离测量误差服从均值uTOA为0、标准差σTOA为5 m的高斯分布，AOA测量误差服从均值uAOA为0、标准差σAOA为1°的高斯分布，k取值为300.

基于上述仿真参数，将本文所提出基于迭代MS定位算法与HLOP算法、内点法（interior point algorithm，IPA）以及GSA进行性能比较，每个仿真独立运行 1000 次.记：无散射半径约束（即式（10）～式（12））为约束条件 1，有散射半径约束（即式（21））为约束条件2.算法描述如表1所示.

表1 算法描述Tab.1 Algorithm description

为了验证本文所提出算法的定位性能，首先仿真研究了上述4种算法在约束条件1下的平均定位误差（mean location error，MLE）随散射半径的变化情况，如图3所示.从图中可见：这4种算法的定位精度都随着散射半径的增大而降低，其中HLOP算法受散射半径影响最明显，此外，本文算法定位精度明显高于其他几种算法，这是由于所提出基于迭代的MS定位算法通过阈值筛选以及加权平均的方式剔除了较大的NLOS误差.

图3 MLE 随散射半径的变化曲线Fig.3 MLE variation with scattering radius

图4是在圆盘散射半径为200 m，各算法MLE对应的累积分布函数（cumulative distribution function，CDF）曲线.由图中可见：本文基于迭代的MS定位算法误差小于200 m就能达到100%，说明基于迭代定位算法可以明显减小NLOS误差对定位性能的影响，并取得较好性能.

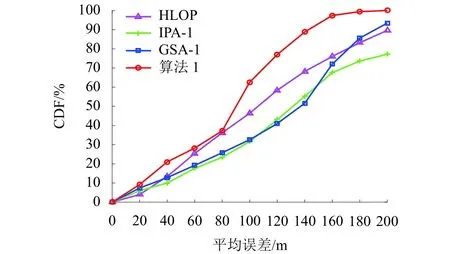
图4 圆盘散射半径为200 m 累积分布函数曲线Fig.4 CDF curves with scattering radius of 200 m

验证增加散射半径几何约束条件是否能提高算法的定位性能，将所提出的基于迭代的MS定位算法与IPA、GSA分别在约束条件1、2下的定位性能进行了对比分析，结果如图5所示.从图5中可见：两种约束条件下，这3种算法定位精度随着散射半径的增加而降低，其中在约束条件2下的算法定位精度下降趋势更加缓慢，说明增加的散射半径几何约束条件能有效抑制非视距误差的影响.纵向来看，本文算法定位性能显著优于其他两种算法.

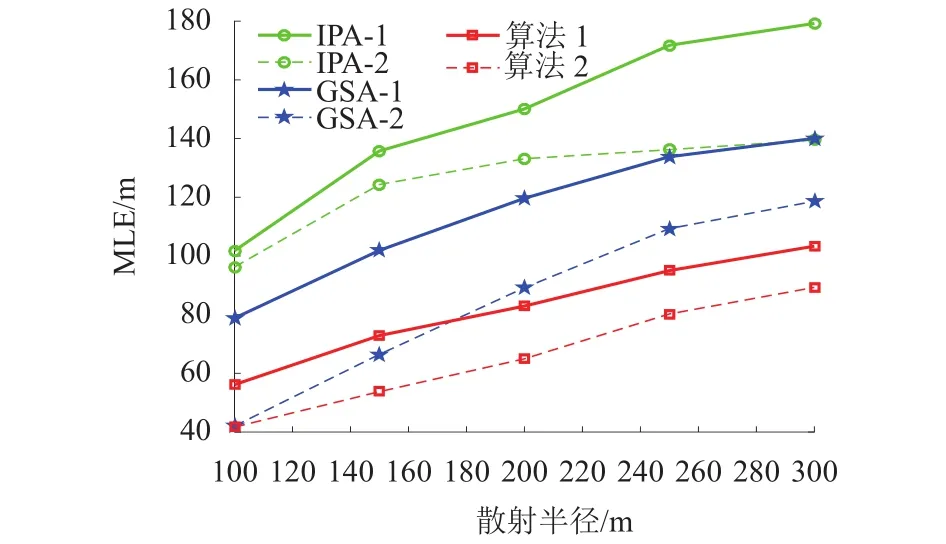
图5 MLE 与有无散射半径约束的变化曲线Fig.5 MLE variation with or without scattering radius constraint

图6所示为最大散射半径200 m时，本文算法、IPA和GSA的MLE对应的累积分布函数曲线.从图中可以看出：使用散射半径约束条件下，这3种算法的性能都能得到提升，且本文算法定位精度明显高于GSA算法，这是由于本文算法采用一维迭代搜索有效值更加逼近中心路径，并且还对得到的MS估计值进行了阈值筛选和加权处理.

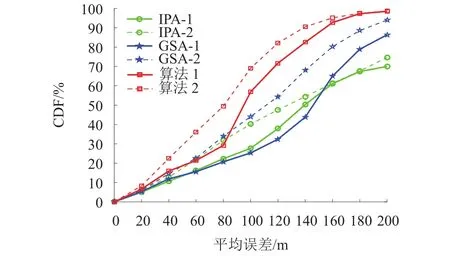
图6 累积分布函数曲线Fig.6 CDF curves with or without scattering radius constraint

为分析TOA距离测量误差与AOA测量误差对定位误差的影响，假定散射半径为200 m，分别在约束条件1、2下对本文算法、IPA和GSA这3种算法性能进行仿真对比.图7和图8分别是改变TOA和AOA测量值标准差时本文算法、IPA和GSA这3种算法对应的MLE变化曲线.从仿真结果可见：随着TOA或AOA测量误差的增加，3种算法的MLE在一定程度上有小幅度上升，说明TOA噪声标准差以及AOA误差对算法影响极小；纵向对比其他两种算法，本文算法具有更好的定位性能.

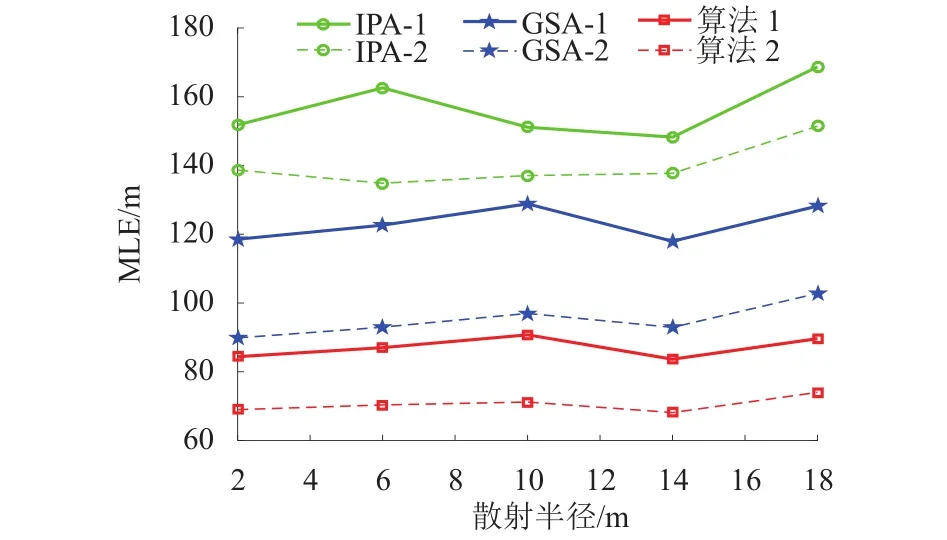
图7 MLE 随距离测量误差的变化曲线Fig.7 MLE variation with distance measurement error

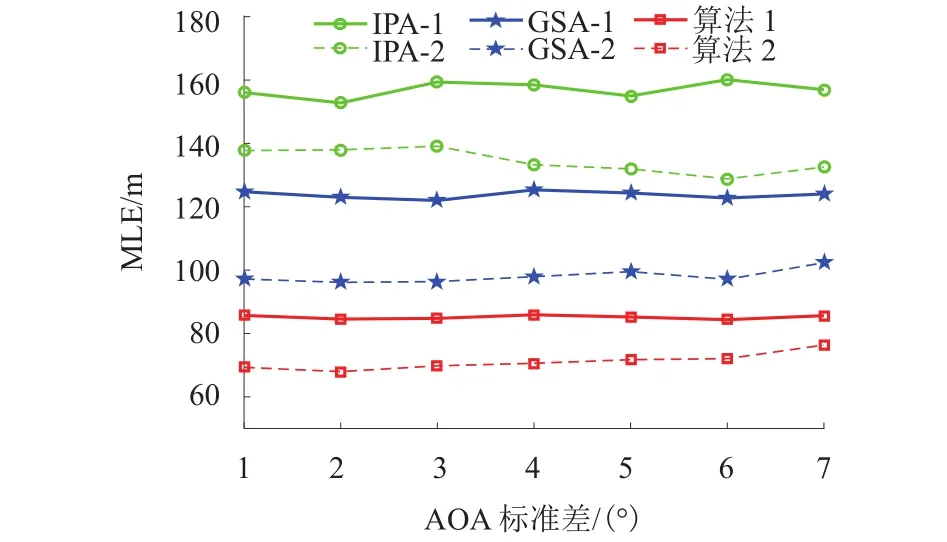
图8 MLE 随角度测量误差的变化曲线Fig.8 MLE variation with angle measurement error

为分析区间长度的划分因子k对MS定位精度的影响，图9给出了在散射半径为200 m时，对应约束条件1和约束条件2下本文算法的平均定位误差和均方根误差随k值变化曲线.由图9可见：在k取0时，由于算法做异常情况处理，因此在有无散射约束时算法误差一致；而随着k取值增加，算法误差有小幅度的下降趋势，这主要是因为k值增加，迭代步长缩小，候选的初始点增加，满足阈值条件估计结果得到提高.且k取700即可得到较好的定位性能.

图9 误差随 k 的变化曲线Fig.9 Location error variation with k

本文还仿真研究了不同算法的计算复杂性.表2给出了3种算法程序在相同环境下运行1000次的平均消耗时间.从表2可见：本文算法耗时最少，且耗时量仅是网格搜索法的0.4%，而在约束条件2下算法耗时进一步减少，这是由于散射半径约束缩小了目标的可行域范围.

表2 算法时间开销Tab.2 Algorithm time cost s

4 结 论

本文提出了一种应用在双基站场景下基于几何约束及迭代的NLOS环境定位算法.通过引入散射信息缩小目标可行域，以一维线性迭代方式进行寻优，有效地规避了传统最优化定位算法需要给定初始估计位置以确保算法收敛这一问题，最后使用阈值筛选以及归一化加权，有效地抑制了较大的NLOS误差对定位精度的不利影响.仿真结果表明，本文算法相比传统的内点法以及网格搜索法表现出更高的定位精度和更低的计算开销.此外，由于仅需两个基站参与定位，在参与定位基站数目受限的室内外环境中具有较大的实用价值.