地铁弹性短轨枕轨道的钢轨波磨萌生原因

李 伟 ，周志军 ，温泽峰

（西南交通大学牵引动力国家重点实验室，四川 成都 610031）

随着我国地铁轨道交通的快速发展和线路减振降噪要求的提高，各种新型结构的减振轨道（GJ-Ⅲ减振扣件、梯形轨枕、弹性短轨枕和长轨枕、橡胶隔振垫、浮置板道床等）被广泛采用，随之带来的减振轨道短波长钢轨波磨问题也越来越普遍[1].短波长钢轨波磨会激励轮轨系统产生连续的中高频冲击振动，加剧轮轨相互作用力，不仅增大轮轨滚动噪声，影响乘客乘坐舒适性，而且其激励的轮轨冲击会引起车辆和轨道零部件所承受载荷频次和幅值变大，导致零部件（车辆一系钢弹簧、轮轴、构架、钢轨、扣件系统等）过早疲劳失效[1]，威胁到车辆运营安全.弹性短轨枕轨道（又称套靴短轨枕轨道）由钢轨、扣件系统和混凝土短轨枕组成，其中，短轨枕通过扣件系统与钢轨连接，通过橡胶垫板与轨道板连接.该轨道通过扣件和轨枕下方的橡胶垫板共同作用来减振，在我国广州、北京等城市地铁线路有使用，在使用过程中轨道钢轨波磨现象较严重[1-2].

对钢轨波磨形成机理的认识是解决波磨问题的基础，波磨产生机理包括固定波长机理和材料伤损机理[3]；固定波长机理表现为车辆和轨道系统共振产生动态轮轨力导致钢轨纵向出现周期性的磨耗，在列车运行速度确定时，该机理会导致固定波长波磨；材料伤损机理包括轮轨磨损行为和钢轨材料塑性变形行为，在车辆轨道系统动态（共振）行为和轮轨磨损行为（或钢轨材料塑性变形）耦合作用下才会形成波磨.因而，波磨产生机理的研究主要从车辆-轨道系统动力学和轮轨磨损两方面开展.

Frederick[4]首次提出了钢轨波磨线性分析模型，基于测量的轨道阻抗特性，通过蠕滑率与力关系，定量分析了轮轨动力响应与钢轨磨耗间的关系，预测了钢轨波磨深度变化状态.Hempelmann等[5-6]结合车辆轨道的瞬态动力模型和轮轨磨损模型，建立了频域下的钢轨波磨预测模型，得到钢轨波磨的形成与轨下支撑刚度较大而引起的较大轮轨接触力有关；Tassilly和Vincent[7-8]利用建立的线性钢轨波磨分析模型，分析了法国的RATP路网内套靴轨枕轨道钢轨波磨的形成原因，认为轨枕共振导致了套靴轨枕轨道曲线的短波长波磨现象；Kurzeck[9]通过SIMPACK软件建立的车辆-轨道动力学时域模型仿真分析了德国斯图加特有轨电车小半径曲线轨道内轨短波长波磨成因，得到短波长波磨的产生主要由车辆运行时激励的轮对一阶弯曲振动和轮对在低轨上表现的P2共振所致；Ahlbek和Daniels[10]调查研究了美国巴尔的摩地铁线路短波长波磨成因，认为车辆通过时，波磨通过频率与轮对自身弯曲和扭转振动模态频率相差较大，轮对横向粘滑振动特性是短波长波磨产生的主要原因；Diana等[11]对意大利米兰地铁线路小半径曲线轨道钢轨波磨的产生原因进行了研究，认为小半径线曲线波磨的产生与轮对自身弯曲振动模态特性无关，主要与曲线轨道阻抗周期性波动和较高的轮轨蠕滑率有关；Vadillo等[12]对西班牙毕尔巴鄂地铁线路小半径曲线的低轨短波长钢轨波磨成因进行了调查分析，认为轨道的横向弯曲振动模态是导致短波长波磨的主要原因，变化轨道轨枕间距（改为0.5 m）可改变轨道弯曲模态频率，从而达到减缓波磨的效果；李伟等[1-2,13-15]通过现场试验和理论仿真分析了我国地铁不同轨道钢轨波磨的形成原因，认为地铁特定波长的钢轨波磨形成主要与轨道结构动态特性相关.

1 钢轨波磨现场调查

为了掌握现场钢轨波磨特征，采用钢轨不平顺测量仪对广州地铁线路A弹性短轨枕轨道区间不平顺进行了测试，测试结果见图1.图2给出了半径R=350 m曲线段轨道内轨钢轨波磨现场照片，其中v为速度，其对应的钢轨局部不平顺结果见图3所示.由图3可知：弹性短轨枕轨道半径350 m曲线内轨不平顺最明显，存在波长约80 mm短波长钢轨波磨现象，波深（波峰与波谷差值）约为0.2 mm.

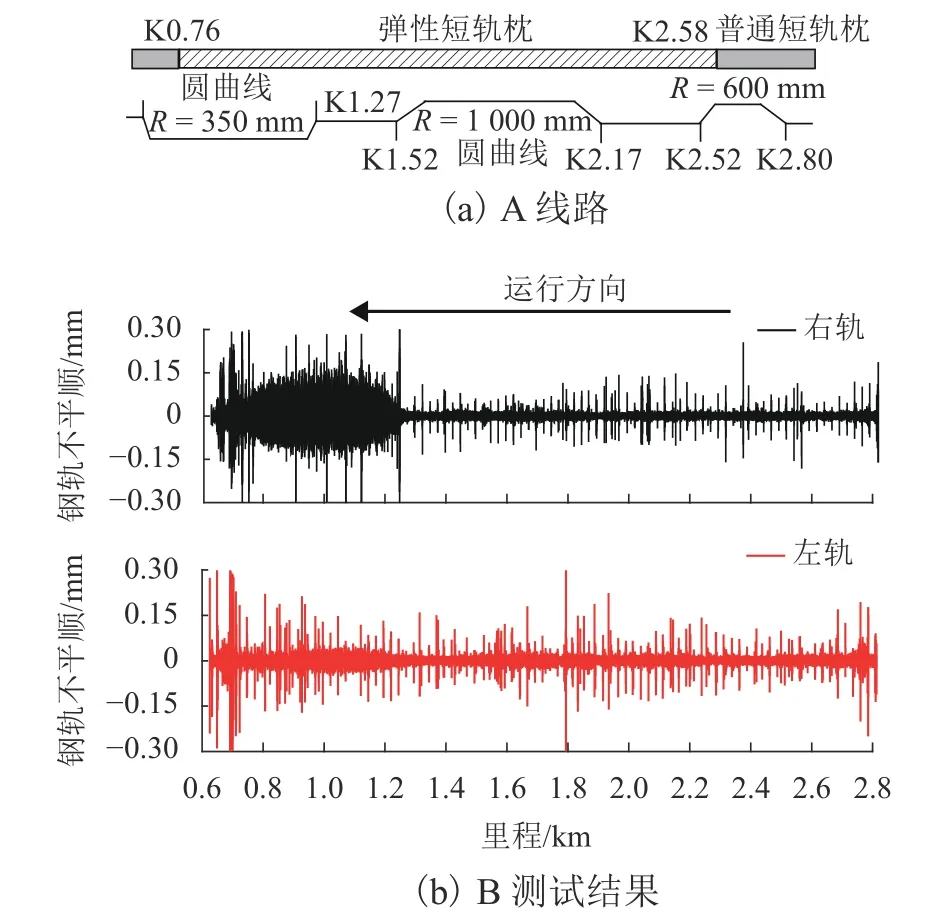
图1 钢轨不平顺测试结果（线路A）Fig.1 Test results of rail irregularity (line A)

图2 钢轨波磨现场照片（线路A，v=55 km/h）Fig.2 Field photos of rail corrugation (line A，v=55 km/h)

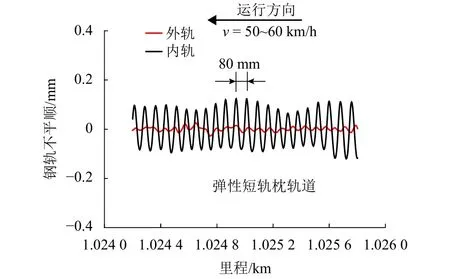
图3 钢轨不平顺的局部放大图Fig.3 Local enlargement of rail irregularity

图4总结了弹性短轨枕轨道在不同半径曲线上的钢轨不平顺水平.表1统计了广州地铁和北京地铁某运营线路的弹性短轨枕轨道钢轨波磨状态.由图表可知：1）弹性短轨枕轨道钢轨波磨现象主要出现在半径R≤ 800 m的曲线段，内轨较外轨严重；半径R＞ 800 m曲线和直线段波磨轻微；2）波磨波长主要表现为50～160 mm；不同半径曲线钢轨波磨波长不同，与车辆运营速度相关；车辆运营速度越高，波长越长；3）基于线路实际的运营速度，弹性短轨枕轨道不同半径曲线段钢轨波磨的车辆通过频率范围为140～280 Hz，为确定性频率特征.

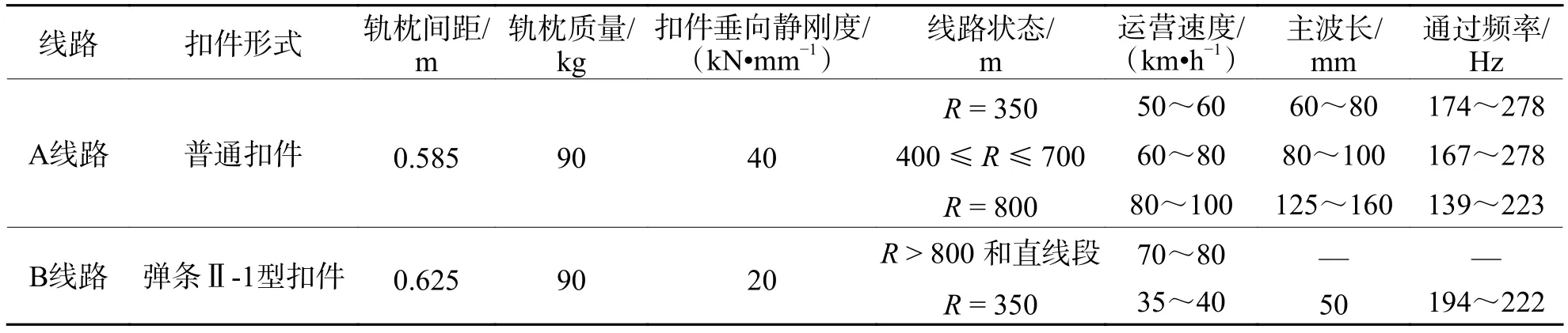
表1 钢轨波磨状态统计Tab.1 Statistical analysis of rail corrugation

图4 钢轨不平顺1/3倍频程谱Fig.4 1/3 octave spectrum of rail irregularity

车辆运行时，轮轨初始不平顺或车辆-轨道参数随机变化的激扰作用会导致轮轨产生振动.当初始不平顺或参数变化激励的轮轨振动频率与车辆-轨道系统（轮对、钢轨、轮轨耦合等）的固有频率接近时，车辆和轨道系统会发生共振，将导致轮轨出现中高频振动，引发轮轨法向力、蠕滑率和接触斑等出现周期性波动，周期性波动的接触参量会导致波磨形成.基于文献[14]，相同车辆在同一运行条件下，两条线路钢轨出现了不同特征的钢轨波磨，调查线路的短波长波磨产生不是由轮对本身固有模态特性所致.下文主要从轨道系统动态特性角度，结合钢轨波磨频域分析模型对弹性短轨枕轨道波磨形成原因进行分析.

2 弹性短轨枕轨道动态特性分析

为获得弹性短轨枕轨道的固有动态特性，采用力锤敲击法测试了没有车辆载荷作用下的轨道动态特性.其中，采用B & K 8 206-002型测试力锤，锤头为塑料型（激励频带为0～2 kHz），锤头激励力为300～1 000 N.通过力传感器测试获得力锤激励力的信号，通过加速度传感器测试获得轨道钢轨和轨枕的响应.加速度传感器分别安装在跨中和轨枕上方的轨头、钢轨下方的轨枕位置，采用单点激励单点响应法获得轨道的垂向和横向位移导纳.通过敲击5次后取平均得到测试结果.

图5为弹性短轨枕轨道在垂向激励垂向响应时的结果，轨道相关参数见表1中线路A.图5（a）为钢轨和轨枕的垂向位移导纳，图5（b）为力锤激励响应的相干系数.参考文献[13]，采用有限元软件ABAQUS建立了弹性短轨枕轨道的三维实体有限元模型，如图6（a）所示，其轨道主要由DTVI扣件、轨枕、弹性套靴、轨道板和地基组成.采用三维实体单元模拟钢轨、轨枕和轨道板，钢轨两端采用固定约束，轨道板两端的横向和纵向自由度进行约束；采用弹簧和阻尼单元模拟扣件系统、弹性套靴和地基支撑.考虑轨道结构的对称性，选取轨道结构的一半进行仿真计算，在轨道中心处设对称边界条件，如图6（b）所示.

图5 轨道垂向动态特性结果Fig.5 Vertical dynamic characteristics of track

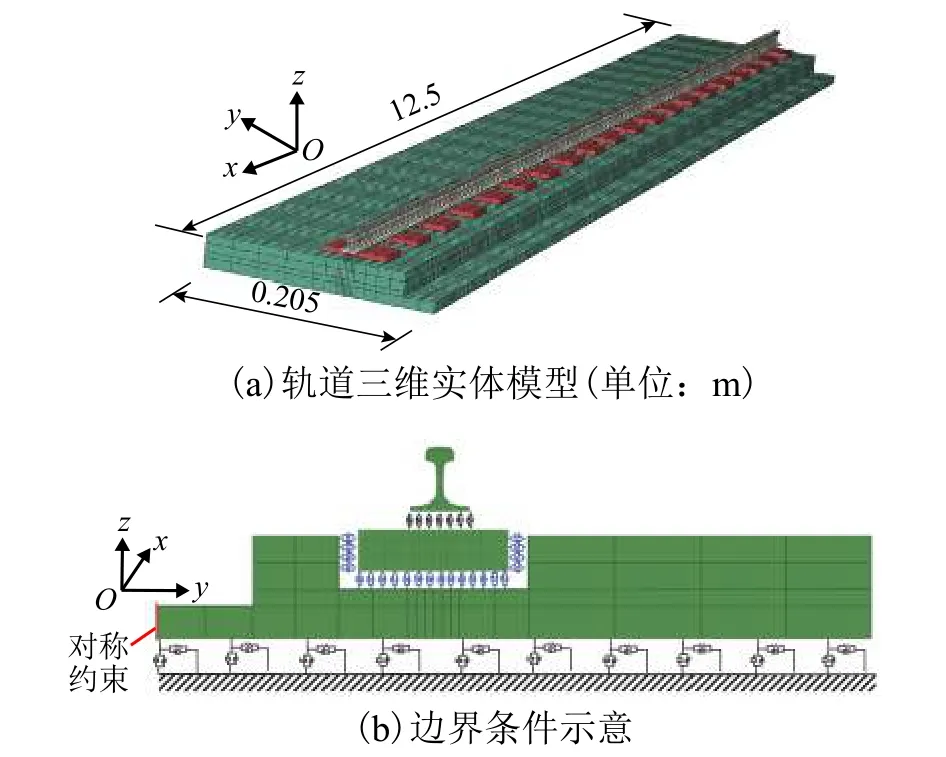
图6 轨道有限元模型Fig.6 Finite element models of track

在数值模型中，钢轨和轨道板长度为一块轨道板长度（12.5 m），轨枕间距为0.585 m，模型包含了23 600个8节点六面体单元和35 796个节点.图7给出了有限元方法获得的弹性短轨枕轨道的垂向振动模态振型.

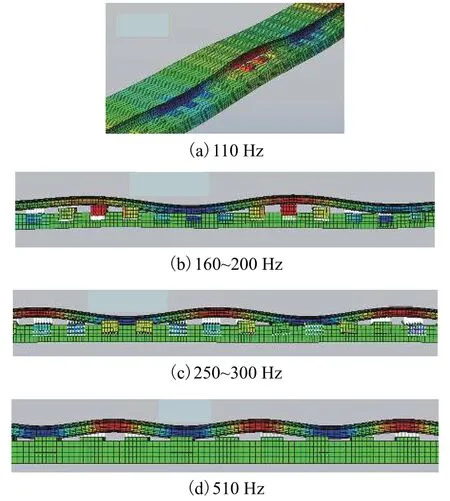
图7 轨道垂向振动模态振型Fig.7 Vertical vibration mode of track

由图7可知：

1）钢轨和轨枕在55～2 000 Hz频带范围内垂向激励垂向响应的相干系数均大于0.8.轨道垂向振动位移导纳在 110、160～210、250～300、510 Hz和1 150 Hz响应明显.

2）力锤在轨枕上方和跨中激励钢轨时，钢轨和轨枕的响应均在约110 Hz时最明显，且二者响应的振动位移幅值相似.轨道在110 Hz的模态振型表现为轨道整体（包含钢轨、轨枕和轨道板）的垂向弯曲振动，见图7（a）.

3）轨道在160～210 Hz的响应特性表现为钢轨和轨枕一起相对轨道板的垂向弯曲振动，且轨枕振动明显，其模态振型见图7（b）.轨道在250～300 Hz 响应特性为钢轨相对轨枕的反向共振现象，且轨枕的振动幅值较钢轨的大，其模态振型见图7（c）.轨道在大于400 Hz频带的响应表现为以钢轨的垂向弯曲振动为主，轨枕的振动相对较小.

4）力锤在轨枕上方和跨中激励钢轨时，轨道在约510 Hz的响应均表现为钢轨自身垂向弯曲共振，见图7（d）.由于轨枕上方钢轨的支撑刚度大于跨中钢轨，因而在单位力作用下跨中钢轨在510 Hz响应幅值大于轨枕上方钢轨.另外，钢轨的1阶垂向Pinned-Pinned共振频率为1 150 Hz，其模态振型表现为钢轨弯曲振动波长等于两个轨跨的距离，且钢轨在轨跨中间的振动幅值最大，在轨枕上方最小[16].

图8为弹性短轨枕轨道横向敲击横向响应结果.

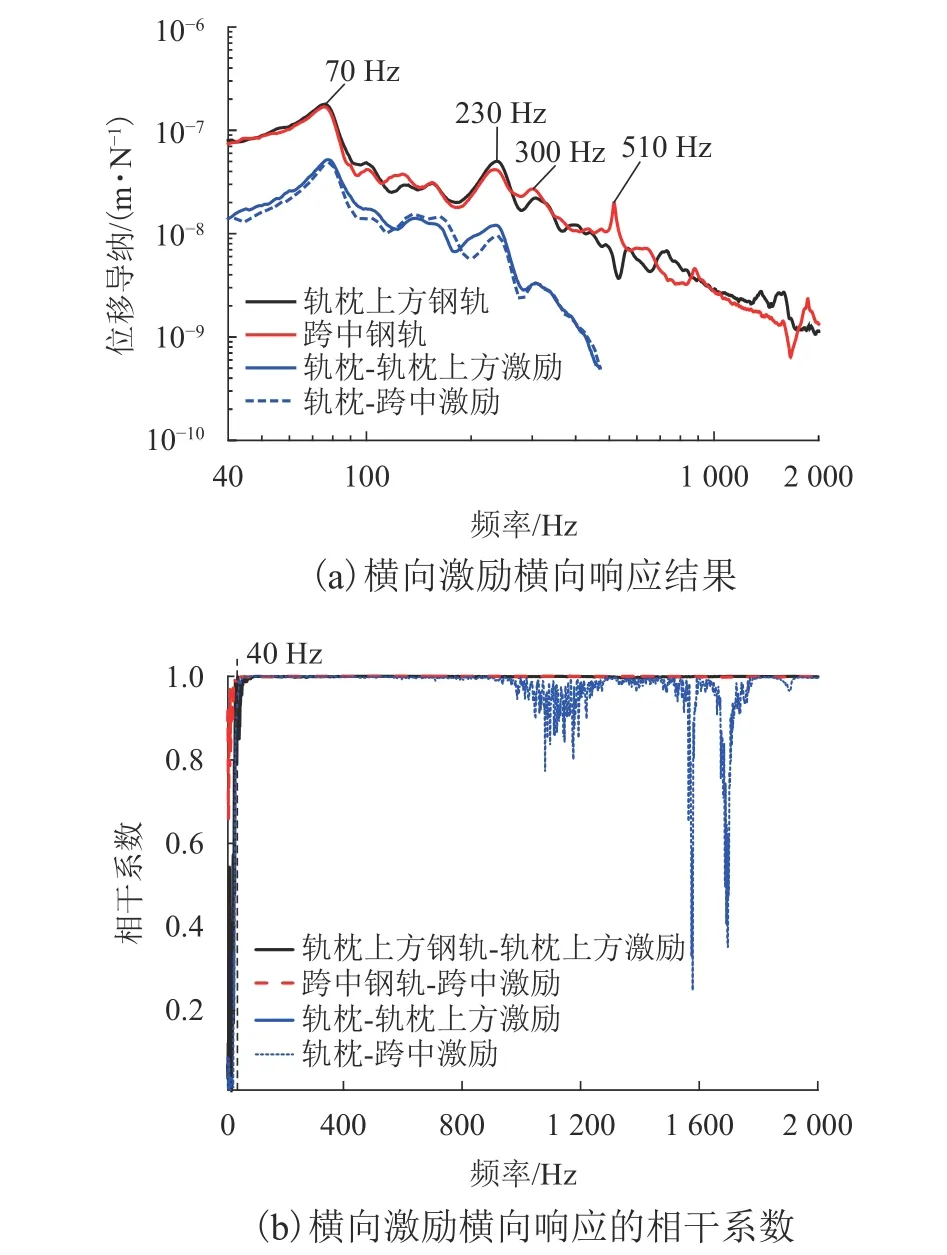
图8 轨道横向动态特性结果Fig.8 Transverse dynamic characteristics of track

由图8可知：

1）钢轨在40～2 000 Hz频带范围内横向激励横向响应的相干系数均大于0.8，弹性轨枕在40～1 600 Hz频带内横向激励横向响应大于0.8.

2）力锤横向激励钢轨时，轨道在40～1 600 Hz响应频段内，轨枕的横向振动幅值相对钢轨的表现不明显.因而，弹性短轨枕轨道的横向振动主要表现为钢轨的横向弯曲和扭转振动，且共振频率表现为70、230、510 Hz等.其中 510 Hz共振模态为钢轨的1阶横向Pinned-Pinned 共振.

因此，弹性短轨枕轨道波磨通过频率（140～280 Hz）与轨道垂向固有模态频率160～210 Hz（模态振型表现为钢轨和轨枕一起相对轨道板的垂向弯曲振动）、250～300 Hz（模态振型表现为钢轨和弹性轨枕的反向振动）和横向固有模态频率230 Hz（模态振型为钢轨的横向弯曲和扭转）相近.为了进一步解释轨道波磨的产生与轨道动态特性相关，借助数值方法对轨道钢轨磨损特性进行了计算分析.

3 数值仿真

为表征轮轨法向力、蠕滑率和接触斑等轮轨接触参数的波动与钢轨纵向不平顺变化的关系，建立了钢轨波磨频域线性分析模型.基于弹性短轨枕轨道现场力锤敲击测试的轨道导纳特性，结合车辆轨道耦合动力学模型计算获得的轮轨滚动接触行为参数，利用建立的钢轨波磨频域线性分析模型[14]，计算弹性短轨枕轨道钢轨磨损率特征.该模型可定性反映轨道动态特性对钢轨纵向磨耗的影响，结合了轮对-轨道结构动态行为模型与钢轨磨损模型，轮对-轨道结构动态行为模型可以考虑轨道动态特性、轮对动态特性和轮轨接触特性.采用Hertz和Vermeulen-Johnson理论分别求解轮轨法向和切向接触问题，采用摩擦功假设来获得钢轨纵向的磨损特征，关于钢轨磨损率的求解过程见文献[14].钢轨踏面沿纵向任意点位置x的磨损率为

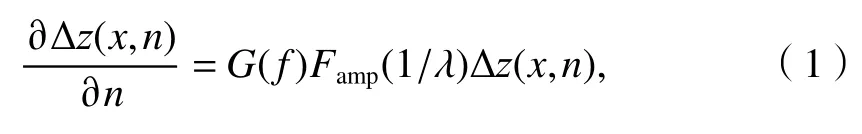
式中：G(f)为钢轨磨损率的表征量，可表示钢轨表面磨损特征与轮轨激励频率的关系；f为波磨通过频率；Δz(x，n)为形成钢轨表面不平顺的型面改变量，n为碾压钢轨的轮对个数；Famp(1/ λ )为幅值滤波函数，λ 为不平顺波长.

关于地铁车辆-轨道耦合动力学模型详细介绍和车辆相关参数见文献[1]；通过该模型计算获得了车辆通过半径为350、600、800 m 曲线时的轮轨法向力、横向蠕滑率、接触斑大小和接触位置的纵向和横向曲率半径，计算结果见表2.模型中：轮轨摩擦系数为0.3；轴重（AW3）为14 t；车轮型面为DIN5573；钢轨廓形为CN60.

表2 轮轨接触参数Tab.2 Wheel-rail contact parameters

图9给出了弹性短轨枕轨道在350 m半径曲线段的钢轨磨损率分布结果，车辆运行速度55 km/h.由图9可知：

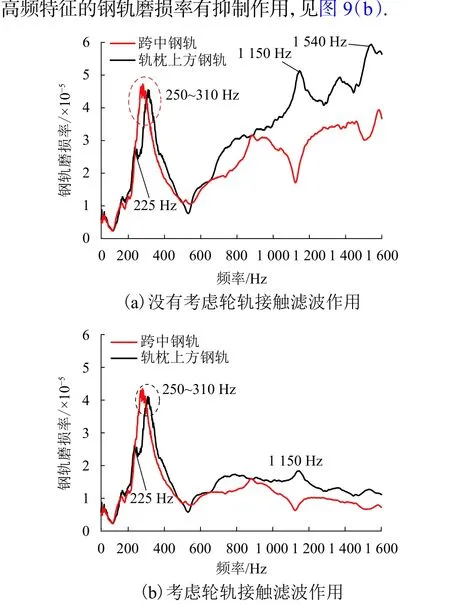
图9 350 m曲线段钢轨磨损率特征Fig.9 Wear characteristics of rails in 350 m curved section

1）仿真模型没有考虑轮轨接触滤波作用时，弹性短轨枕轨道轨枕上方钢轨磨损率在高频段（1 150 Hz和1 540 Hz）表现最明显，该高频特征的磨损导致的钢轨波磨波长较短（10～13 mm）.由于轮轨接触斑具有滤波特性作用[17-18]，考虑轮轨滤波效应后（具体计算方法见文献[18]），轮轨接触滤波作用对大于600 Hz

2）仿真模型考虑了轮轨接触滤波作用后，无论是轨枕上方还是跨中的钢轨，均在225～310 Hz 频带的磨损率表现最大，而在大于600 Hz频带的磨损率表现较小.这是由于弹性短轨枕轨道钢轨垂向位移导纳值在250～300 Hz频带表现低（出现钢轨和轨枕垂向反向共振现象，见图5（a）和图7（c）），易导致较大的波动轮轨力，带来该频带较大的钢轨磨损率，从而萌生该频率特征的波磨现象.

图10为弹性短轨枕轨道不同半径曲线段（600 m和800 m）的钢轨磨损率计算结果.由图10可知：随着轨道曲线半径的增大，轨道钢轨的磨损率明显减小，这是由于轮轨横向蠕滑率随着曲线半径的增大而减小（见表2）；弹性短轨枕轨道在不同半径曲线段的跨中和轨枕上方钢轨的磨损与半径350 m的钢轨磨损特征相似，即均在 225～310 Hz 频率范围内钢轨磨损率表现最为明显，这与轨道在250～300 Hz范围具有钢轨和弹性轨枕的反共振模态特性有关，由于钢轨在该频带表现刚度较大，其导致的波动轮轨力相对较大所致.因而，弹性短轨枕轨道钢轨形成的波磨特征表现为频率固定型，波磨波长与车辆运营速度相关，随着车辆运营速度的提高，其导致的波磨波长会增大.

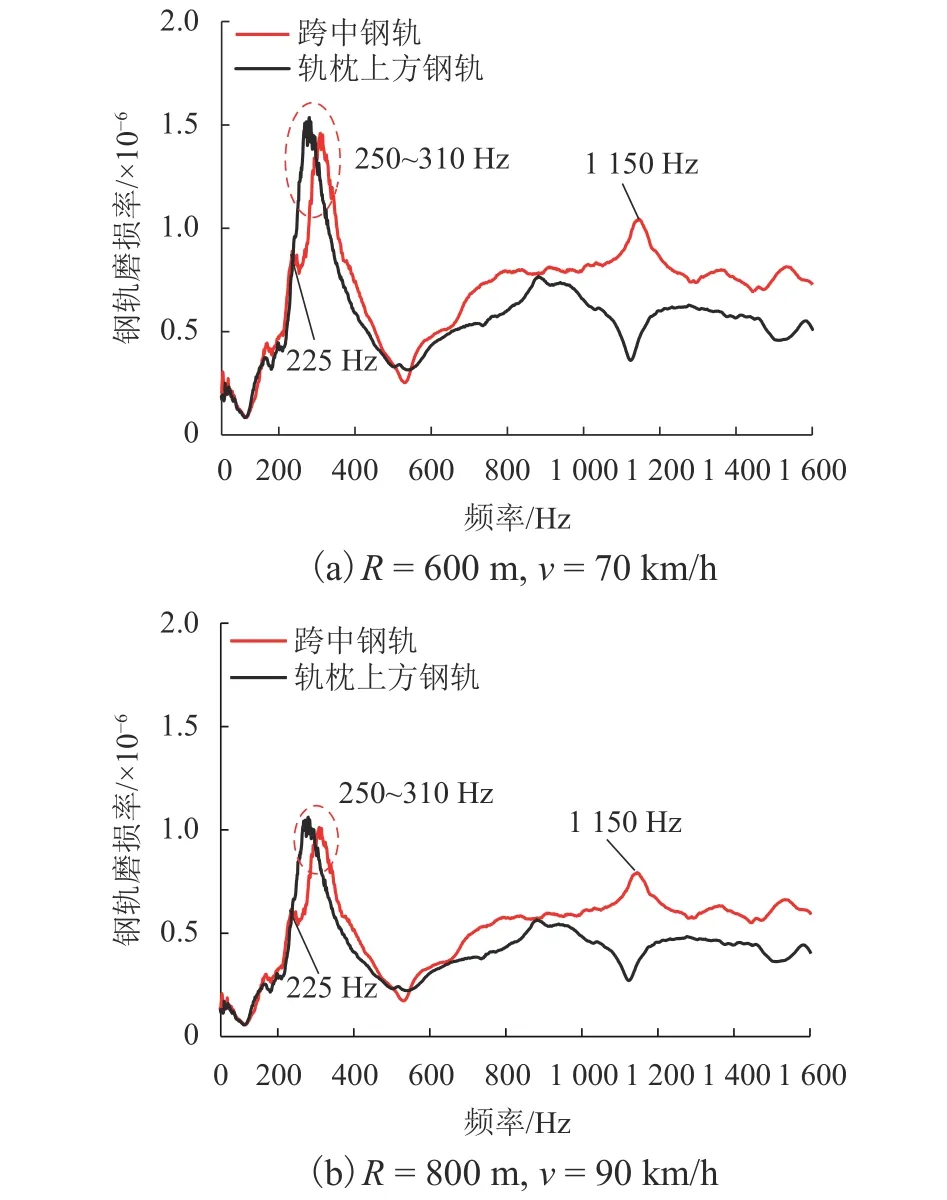
图10 曲线半径对钢轨磨损率的影响Fig.10 Influence of curve radius on wear rate

根据波磨波长=v/f可知：弹性短轨枕轨道在半径350、600、800 m曲线的钢轨磨损波长分别为44～74、54～99、72～124 mm，与线路 A 现场测量的波磨波长（60～80、80～100、125～160 mm）相近，但有一定偏差.这种差异可能与车辆加载与否相关，由于轨道扣件和弹性套靴的垂向刚度受到车辆载荷大小和频率的影响，因而轨道垂向动态特性也会受到车辆加载作用的影响，车辆载荷对轨道垂向动态特性的影响频率一般小于400 Hz，对高频影响较小[19].由于现场试验条件限制，没有测量车辆加载时的轨道垂向动态特性.另外，由于地铁车辆通过大半径曲线和直线轨道时，轮轨蠕滑率较小，导致的钢轨波磨不明显.

在轮轨初始不平顺激励下，由车辆系统（轮对扭转共振）或轨道系统（轨枕共振、钢轨Pinned-Pinned共振）或轮轨耦合系统（P2共振）等共振时引起的车辆轨道系统动态行为会导致轮轨力和蠕滑率的波动[20]，波动的轮轨法向力和蠕滑率会引起钢轨沿纵向产生周期性的磨耗即钢轨波磨[21-22].轮轨纵向和横向蠕滑率主要决定于轮对左右滚动圆轮径差和轮对摇头角.车辆通过曲线时，曲线半径大小会影响轮对横移量，进而影响轮对左右滚动圆轮径差，从而影响轮轨纵向蠕滑率.另外，曲线半径越小，轮对摇头角会越大，产生横向蠕滑率越大（见表2），导致轮轨摩擦功增大，从而导致轮轨磨耗变大，在车辆轨道系统共振状态下引起的波磨严重.

4 结 论

1）地铁弹性短轨枕轨道钢轨波磨主要出现在小于等于800 m半径曲线段，波长表现为50～160 mm，通过频率范围为140～280 Hz.波磨通过频率与弹性短轨枕轨道垂向的固有模态频率160～210 Hz和250～300 Hz相近；二者模态振型分别表现为钢轨和轨枕一起相对轨道板的垂向弯曲振动、钢轨和弹性轨枕垂向反向振动.

2）不同半径曲线的弹性短轨枕轨道钢轨磨损率均在225～310 Hz频带表现最明显，曲线钢轨磨损表现波长为50～112 mm，与现场测量的基本吻合；形成的波磨特征表现为频率固定型，波磨波长与车辆运营速度相关.

3）弹性短轨枕曲线段短波长波磨产生主要与轨道存在160～210 Hz和250～300 Hz范围的垂向固有模态特性相关.