城际动车组车轴应力谱的极值推断

2021-07-02王文静

西南交通大学学报 2021年3期

丁然，李强，王文静

（北京交通大学机械与电子控制工程学院，北京 100044）

车轴是车辆的关键承载部件，其疲劳断裂将造成列车脱轨或倾覆等重大事故，给国家财产和乘客的生命安全带来巨大的损失.现行的车轴设计规范，如日本的JIS E 4 501[1]、欧洲的 EN13103[2]及EN13104[3]等，均要求车轴关键截面所受的最大应力不得大于材料的疲劳许用应力.材料的疲劳许用应力可利用材料实验测得的疲劳极限与适当选取的安全系数相除得到；获取车轴所受的最大应力最直接最可靠的方法是在轴身上贴片，通过线路实验直接测量关键截面处的应力.

城际动车组的速度等级和线路条件等均与高速动车组有很大不同，因此有必要对其作进一步的研究[4-8].然而线路测试由于受人力、物力成本及测试时间等客观因素的限制，测试里程通常只有数几千公里.为了评估车轴的可靠性需要扩展应力谱或推断其寿命周期内的最大应力值.

利用应力谱或载荷谱进行外推的主要方法是先对之进行分布拟合，再利用拟得的最佳分布进行外推.目前的研究多集中在如何提高分布的拟合能力及多工况分别拟合时如何计算综合应力极值[9-11]，然而这种方法有时会有很大的偏差[9,12].另一种外推方法是扩展因子法[12-13]，但此法只能用于标准累积频次谱的外推.由于标准谱的参数较少，形状比较单一，很难用来拟合线路实测的结果.本文将使用拟合超限分布函数的方法进行应力谱的极值推断.其理论基础为极值理论，目前多用于土木工程[14-15]及金融保险领域[16]，尚未见应力谱或载荷谱推断等方面的应用.

1 线路测试及应力谱编制

本文测试线路为成达线（成都––达州），单程约380 km，混合了既有线路和新修线路，整体特点是多弯多隧道.测试时全车装载沙袋模拟满载工况，测试总里程约为3 000 km.

在测试轮对的轴身上选取 7 个截面进行贴片：两侧轮座至轴颈间各选取 2 个截面，两轮座之间选取 3 个截面，将截面依次记为A～G，如图1所示.除截面D外，其它截面的贴片处均为过渡圆弧根部，这些地方会有不同程度的应力集中，有较强的应变响应.有关测力轮对贴片、标定以及线路测试的其它细节可进一步参考文献[6].

图1 车轴测试截面位置Fig.1 Test sections on axle

对测试结果进行雨流计数即可获得各测试截面所受应力S的统计信息.计数前需要确定应力分组的组数k和组距h，如式（1）所示.

式中：smax和smin分别为实测应力s的最大值和最小值.

评估损伤或统计应力谱特征时，k不宜取得过小.目前确定k或h有一些经验公式[17]，对应计算结果见表1.表中：nt为统计所得的应力循环总数；σS、QS分别为S的标准差、四分差.

表1 不同经验公式的组距计算结果Tab.1 Calculated results by different empirical formulas

推断应力极值时更关心较大应力幅对应的小概率事件，因此h也不宜取得过小.综合考虑后，取h=0.50 MPa.对截面A～G的实测应力分别进行雨流计数，应力谱如图2 所示.

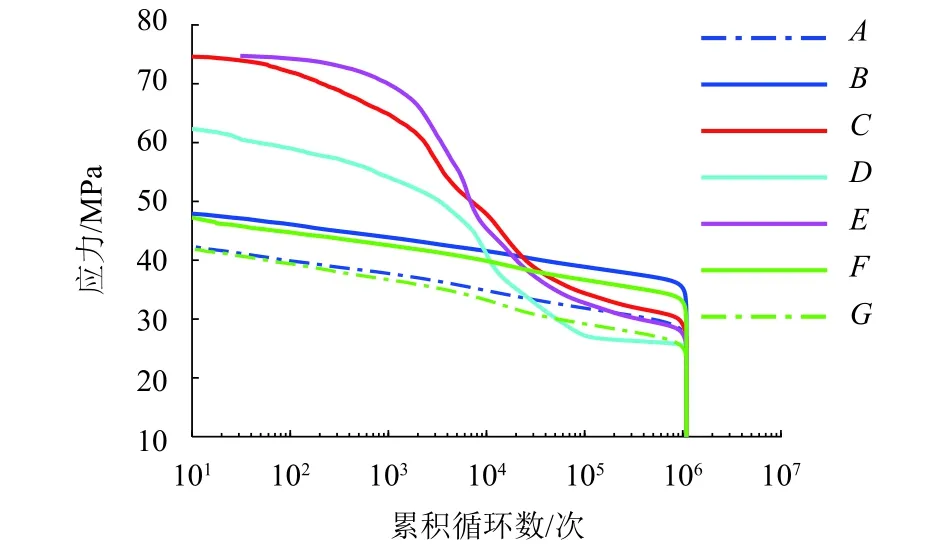
图2 各个截面的应力Fig.2 Stress of each section

2 分布拟合法

工程上通常将发生概率小于10−6对应的S作为其最大值的估计[11].若记随机变量S的累积分布函数为F(s)，则smax=F−1(1 − 10−6) ，F−1(•) 为F(•) 的反函数.以截面B为例，分别用正态分布、对数正态分布（LN）、两参数和三参数威布尔拟合其应力分布，并用拟合得到的分布计算smax，结果见表2.表中：为对数正态分布的卡方统计量；χ2为正态分布、威布尔分布的卡方统计量。

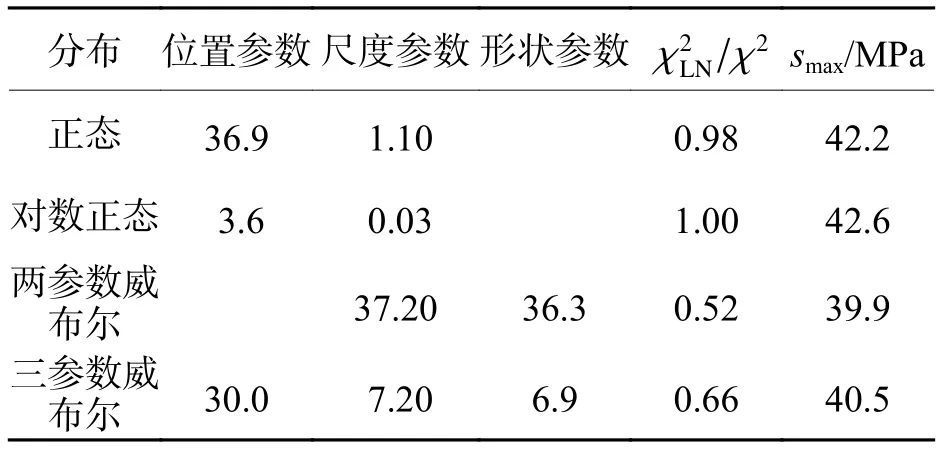
表2 截面 B 的分布拟合结果Tab.2 Fitted results of section B

表2的4个备选分布中对数正态分布的卡方统计量最小，表明它的拟合效果最佳.因此可在一定程度上反映不同分布的拟合优度.表2结果表明：正态分布的拟合效果略逊于对数正态分布，二者均优于威布尔分布；三参数威布尔分布优于两参数威布尔分布.这些备选分布的拟合效果见图3.由图3可明显看出：这些分布对数据中部（高频区）的绝大多数数据有较强的描述能力，但对尾部（低频区）的描述能力较差.备选分布中对数正态分布推得的smax最大，为42.6 MPa，由图2截面B的实测结果可知，应力大于43.0 MPa的发生频率约为104/106=1%，与预期的10−6相去甚远.

图3 不同分布概率密度市函数与累积分布函数的拟合效果Fig.3 Fitted probability density function and cumulative distribution function with different distributions

事实上，由于采集的样本量较大，这4个备选分布均不能通过对应的假设检验.使用 χ2统计量的比值作为拟合优度，主要也是为了反映这4个备选分布之间的相对优势.利用组合分布能在一定程度上提高分布的拟合能力，但是对提高分布尾部的拟合能力效果有限.对于车轴来说，一般两轮座之间的应力分布（如截面C～E）要比轮座外的应力分布更复杂（如截面A、B、F和G），见图2.因此若不能找到合适的备选分布就会很大程度上限制分布拟合法的推断精度.该结果也表明使用常见分布很难充分描述车轴的应力分布，尤其是很难准确描述较大应力的发生规律.

3 极值理论与极值推断

直接使用分布拟合法外推会产生较大误差，主要原因是一般的统计模型侧重于描述绝大多数（高概率区）数据的行为，因此用来推断极少发生的应力极值效果欠佳.本文依据极值理论中的第二极值定理[15,18]（又称 Pickands-Balkema-de Haan 定理）进行推断，为此需引入超限分布函数的概念.任一实数u，S的超限分布函数为

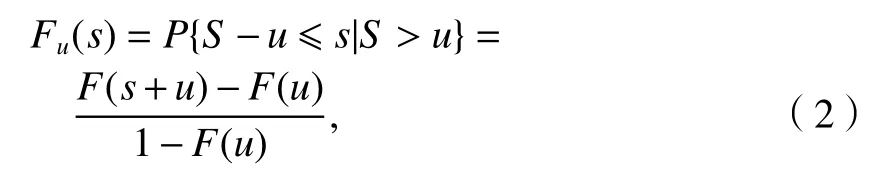
式中：P(•)为概率函数.

从定义中可以看出Fu(s) 只与S＞u的分布尾端相关.若S代表疲劳寿命，则超限分布就是已知寿命不小于u时的剩余寿命分布.因此超限分布可以看成剩余寿命分布这个概念的推广.第二极值定理断言，对于满足一定条件的分布函数，必存在系数β＞0，使得

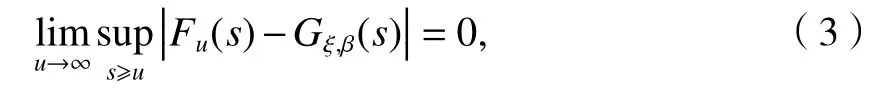
式中：Gξ,β(•) 为以ξ和β为参数的广义帕累托分布（generalized Pareto distribution）函数，如式（4）所示.

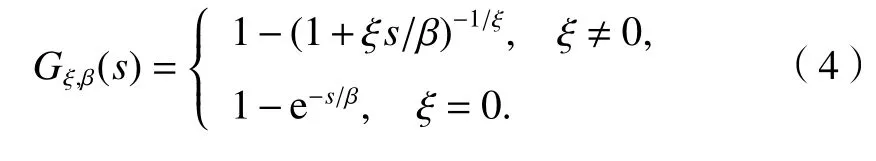
满足该定理条件的函数集合称作极值分布Hξ的最大值吸引域.该函数类非常广泛，几乎包括工程应用中可遇到的所有连续分布函数.Hξ的最大值吸引域的具体表示涉及较深的概率统计知识，可进一步参考文献[15,16,18].该定理表明，在一定程度上，无论S服从何种分布，对于充分大的u总可以用Gξ,β(s)来做Fu(s) 的近似.

在用Gξ,β(s) 拟合应力谱的超限分布之前，还需先确定一个充分大的u，以确保拟合的精度.Gξ,β(s)的均值超限函数（mean excess function）为线性函数，记为e(u)，是S−u在S＞u下的条件均值，即

利用e(u) 为线性函数这一性质，可以先作出原分布e(u) 的图像，若大于某点后e(u) 近似为一直线，则可取u为该点，进而用Gξ,β(s) 去拟合原分布的超限分布Fu(s).

若拟合效果良好，即可用Gξ,β(s) 外推出应力极值.如估计发生概率不大于 10−6的应力，可表示为

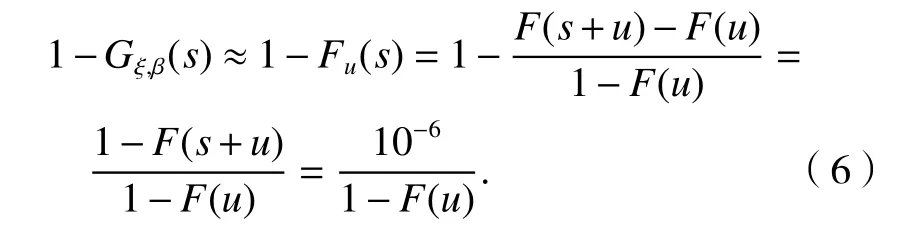
式（6）代入式（5），得近似方程为

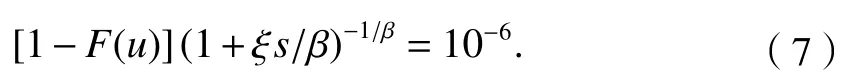
即

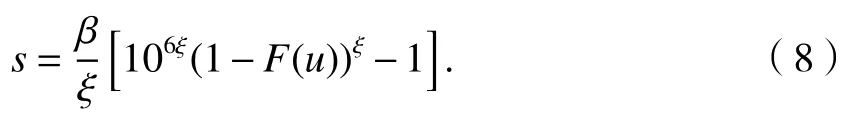
根据超限分布函数的定义可知S−u＞s的概率小于 10−6，因此可取smax=s+u.该方法不仅可用于车轴应力谱的推断，也可以用于其它构件应力谱或载荷谱的极值推断.

计算截面B应力分布的均值超限函数，如图4所示，可知在u=37 MPa附近e(u) 有一个较大偏转，之后近似为一条直线.若取u=38 MPa，并用Gξ,β(s)去拟合Fu(s)，通过极大似然法可估得ξ和β的估计值分别为=0.023，=1.03，拟合效果见图5.图中两条曲线几乎完全重合，说明取u=38 MPa已达到使二者充分接近的要求.将拟得参数代入式（8）可算得s的估计值=11.2 MPa，因此，smax=(+u) MPa=49.2 MPa.该值略大于实测应力的最大值 48.5 MPa.

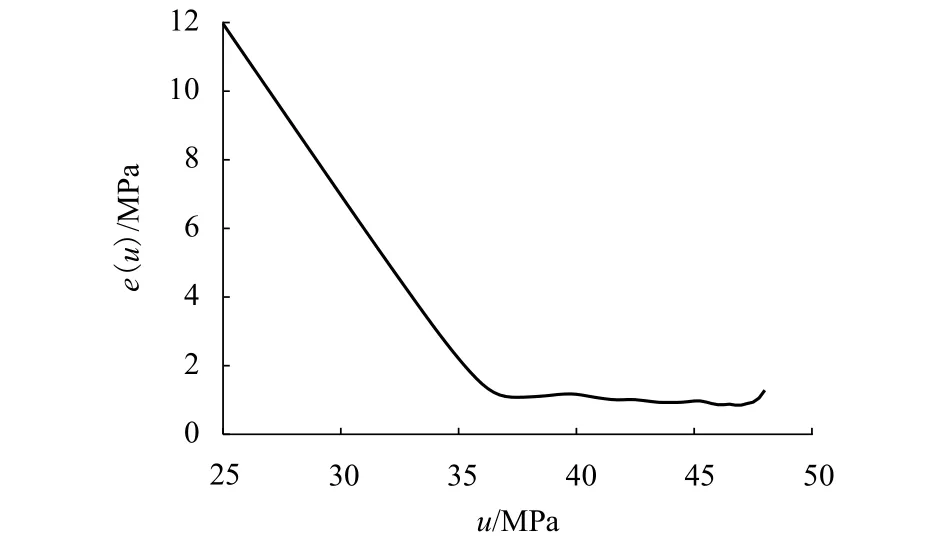
图4 截面 B 应力分布的e(u)Fig.4 e(u) of stress distribution for section B

图5 截面 B 的 Fu(s) 拟合效果Fig.5 Fitted Fu(s) of section B

参数ξ在极值理论中有重要意义，其倒数α=1/ξ反应了分布原点矩的最大阶数.任何阶数r＞α的原点矩必发散，即

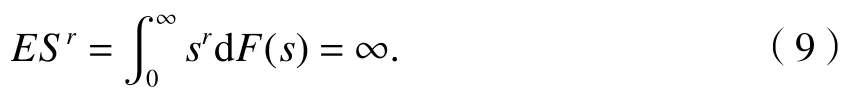
若α＜ 4（或等价地ξ＞ 0.250），表明F(s) 是严重偏态的分布；若α＜ 2（或等价地ξ＞ 0.500），则F(s) 是重尾（heavy-tailed）分布.对于这些情况，增加测试里程将会以相对更大的概率观测到明显高于smax的应力值.此时用 106次载荷循环的测试结果外推全寿命周期下应力的极值需十分谨慎.本文测试截面均有

车轴的安全性评估不必从统计效率最大化的角度考虑问题.作为工程应用，可计算在u不同取值下的smax（图6），并取smax中的最大者为，这样可得到更加保守的推断结果.截面B的为53.3 MPa，对应的u值为46 MPa.由图6可知smax的取值基本稳定在 50.0～53.0 MPa，说明本文的估计方法是比较有效的.如果smax随u的变化剧烈，需再次检验Gξ，β(s)的拟合效果，并谨慎对待推断结果.其它截面的推断结果见表3.

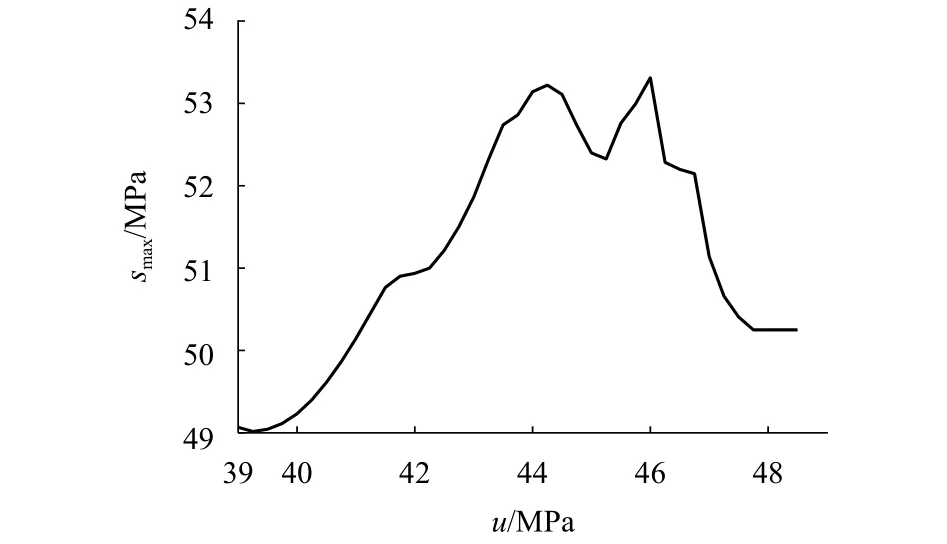
图6 u 取不同值时 smax的变化Fig.6 smax under different values of u

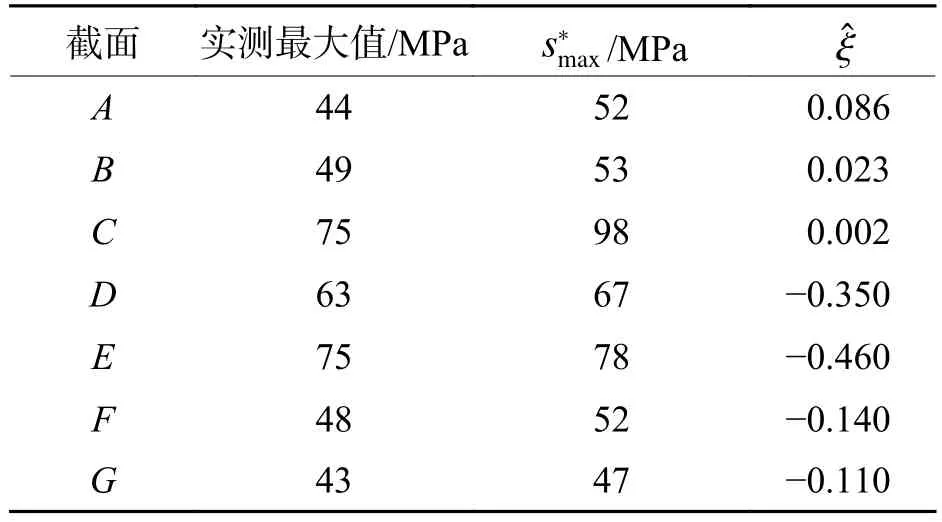
表3 各截面的实测最大值与应力的极值推断结果Tab.3 Measured maximum values and extreme value inferences of each section

本文测试的总应力循环数已经达到106（见图2），因此直接以测试结果的最大值作为smax的估计也可算作一种方法.表3 也分别列出了各截面的实测最大应力值.对比实测最大值与可知截面E、G二者大致相当，而截面A、C则相差较大，似乎不易发现二者间的必然联系.由于极小概率事件的发生有很强的随机性，因此，仅用最大值作为统计结果可能会出现较大偏差.

4 车轴的安全性评价

车轴除了在设计时须确保安全余量，一般在运营时也会保留一定的安全余量.本文测试车轴的设计轴重为17.0 t，生产方规定的最大运营轴重为14.1 t，本文实测满载工况的轴重大约在 13.5 t 上下.根据EN13104[3]，可算出不同的轴重下的校核应力，如表4所示.其中部分截面（如截面B、C、F）推得的要大于 13.5 t 甚至 14.1 t 轴重算得的校核应力.截面C的推断极值要比 14.1 t 轴重的校核应力高出 |98−86|/86×100%=13%.这意味着若按 17.0 t 轴重满载运营，车轴寿命期内的最大应力有可能超出标准规定的最大许用应力.因此运营时若不保留安全余量，完全按照设计轴重满载运营，需格外谨慎.

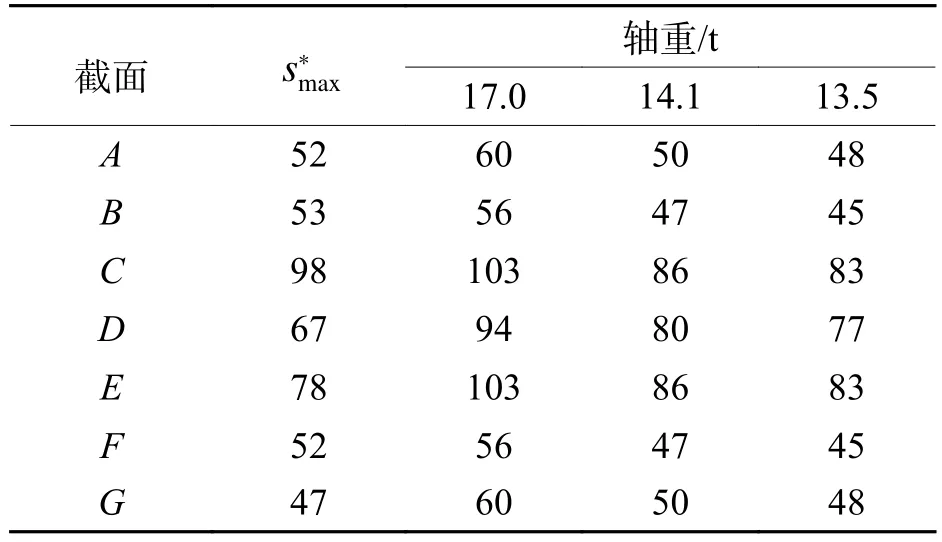
表4 与校核应力的对比Tab.4 Comparison between and allowable stresses MPa

截面 images/BZ_192_1567_2772_1630_2814.png轴重/t 17.0 14.1 13.5 A 52 60 50 48 B 53 56 47 45 C 98 103 86 83 D 67 94 80 77 E 78 103 86 83 F 52 56 47 45 G 47 60 50 48

由于标准中计算校核应力时考虑的是车轴运用的最差工况，叠加了偏载、过曲线、制动等的影响，因此算得的应力应当无法在实际运用中达到.虽然推断极值受测试设备精度和统计精度的影响会有一定误差，但该结果足以说明车轴的实际运用工况十分复杂.本文测试车轴各截面的值均小于按设计轴重 17.0 t 算得的校核应力，从而也不超过标准规定的材料最大许用应力.因此线路实测的分析结果表明，车轴的疲劳强度满足标准的要求.