基于头脑风暴优化的PCNN路面裂缝分割算法

范新南 ，汪 杰 ，史朋飞 ，李 敏

（河海大学物联网工程学院，江苏 常州 213022）

路面裂缝反映了道路的损坏程度，事关道路交通的安全，所以对于裂缝的检测必须予以重视.传统的路面裂缝人工检测耗时费力，随着科技的发展，越来越多的新技术应用到裂缝检测上.常见的裂缝分割方法有：基于阈值的分割[1]、基于局部和全局特征的分割[2]、基于图像显著性的分割[3]和基于神经网络的裂缝图像分割[4].前三类方法往往有复杂的预处理过程，而神经网络算法可直接将裂缝图像作为输入，但较传统方法而言，模型复杂，训练时间较长.脉冲耦合神经网络（pulse coupled neural network，PCNN）是单层神经网络，依据图像的自然属性进行图像的分割.宋蓓蓓等[5]基于PCNN模型实现裂缝的粗提取，但裂缝存在断裂且噪声干扰大.这是由于PCNN模型参数多而且设定复杂，关键参数需多次试验人工调整，不同的参数会导致不同的分割效果.

张坤华等[6]将粒子群算法和基于单调递增阈值搜索策略的改进PCNN模型相结合，自动寻优连接系数和迭代次数.周东国等[7]利用动态阈值与区域均值之间的关系，给出连接系数、动态阈值的幅度系数的确定准则，对灰度混叠的图像表现出较好的性能，但如果图像中同时存在亮目标和暗目标，会出现忽略暗目标的情况.这些改进的PCNN方法仅是针对特定的图像，用在复杂裂缝图像上的有效性有待验证.赵慧洁等[8]提出一种基于最小误差准则的PCNN裂缝图像分割方法，通过寻找最佳迭代次数实现对裂缝的有效分割，但是需要通过后续去噪去除干扰.宰柯楠等[9]采用遗传算法优化PCNN参数，完成对动态阈值时间参数、阈值放大系数、连接系数的自动设定，取得较佳的裂缝图像分割效果，但在分割含有较大像素的裂缝图像时，运算时间过长，且裂缝出现断裂、不连续的情况.

头脑风暴优化（brainstorming optimization，BSO）是近几年兴起的群体智能优化算法，BSO算法搜索效率高，全局寻优强[10-12].本文利用BSO自适应寻优PCNN参数，创新性地将PCNN与BSO算法结合，采用最大熵原则，实现了自动寻找PCNN模型参数的最优值完成裂缝图像的分割.

1 BSO-PCNN裂缝分割算法

1.1 基于PCNN图像分割模型

PCNN是基于哺乳动物视觉信息处理机制而提出的第三代神经网络模型，具有全局耦合性、同步发放脉冲的特性.神经元与邻域内的神经元组成反馈网络相互影响.PCNN模型由接收部分、调制部分以及脉冲产生部分组成，能较好地模拟神经元的特性，每个神经元对应于图像中的相应像素点.

当PCNN应用于图像分割时，影响分割效果的主要参数有动态阈值参数θ、连接系数β、阈值调节参数ε、衰减时间∂L.这些参数的选择一般先是凭经验确定，每幅图像通过大量试验手动调整参数.这种方法不仅费时费力，而且无法适用于不同类型的图像.因此，为减少人的主观性，如何自动确定PCNN参数显得尤为重要.

1.2 BSO算法模型

1.2.1 BSO 算法组成部分

BSO算法可以解决不同的优化问题[13-14]，其主体由5个部分组成：初始化、聚类、替换、生成以及选择过程[15].

1.2.2 BSO 算子

聚类算子和生成算子是影响BSO算法效果好坏的关键[16].聚类算子模拟了不同想法划分为不同类的过程，将相似的个体聚为一类，本文选择K-means作为聚类算子.生成算子模拟了新想法产生的过程，新个体对下一次的迭代影响很大，这里采用高斯变异法[17]，具体如式（1）所示.

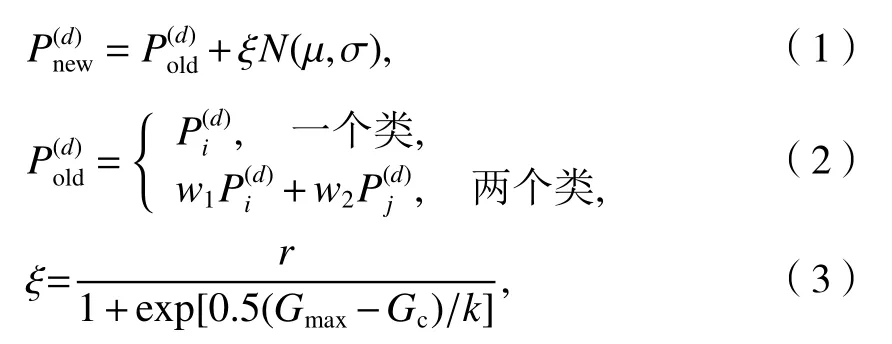
1.2.3 适应度函数

熵是图像中的一个重要概念，表示不确定性.本文采用最大熵准则[18]作为BSO算法的适应度函数.

1.3 BSO-PCNN裂缝图像分割算法

步骤1参数初始化.

将PCNN动态阈值参数θ初始化成种群个体.设定d=1；种群规模S=40；个体最大值Xmax=255，最小值Xmin=0；通过初始化随机生成40个个体P1、P2、···、P40；确定Gmax=50；聚类数为4；聚类中心被替代的概率pr=0.1；选择1个聚类的概率p1=0.5，选择1个聚类中心的概率pc1=0.3，选择2个聚类中心的概率pc2=0.2.

步骤2K-means聚类.

通过计算每个个体与其他个体之间的欧式距离，将40个不同的个体分配到4个不同的类中.

步骤3根据适应度函数评估个体.

计算图像直方图信息，统计每个像素的概率分布.根据最大熵公式计算每个类中每个个体的适应度，选择最优的个体作为该类的类中心.

步骤4聚类中心的替换.

随机产生一个数r1∈(0,1)，与预先设定的概率值pr比较，如果r1＜pr，则从不同的类中随机选中一个聚类中心Pc，用一个随机个体去取代这个选中的聚类中心.

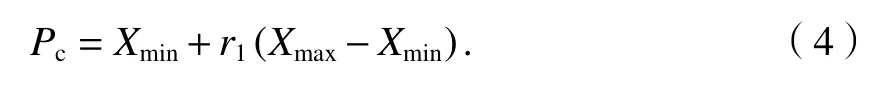
步骤5新个体的产生.

1）在0和1之间生成一个随机值r2；

2）若r2＜p1，

① 在类中随机选择一个类；

② 在0和1之间生成一个随机值r3；

③ 若r3＜pc1，对已选中的类中心通过高斯变异法加上随机扰动来产生新的个体；若r3≥pc1，从选中类中随机选择一个个体通过高斯变异法加上随机扰动，来产生新个体，如式（1）所示.

3）若r2≥p1，随机选择两个类：

① 在0和1之间生成一个随机数r4；

② 若r4＜pc2，选择两个类的聚类中心Pc1、Pc2，将他们融合产生高斯变异前个体Pold,c，再添加一个随机扰动产生高斯变异新个体Pnew,c，如式（5）所示；

③ 若r4≥pc2，从两个聚类中随机选择两个普通个体Pp1、Pp2，将它们融合产生高斯变异前个体Pold,p，再添加随机扰动产生一个随机扰动产生高斯变异新个体Pnew,p，如式（6）所示.

步骤6个体选择.

将新个体与本次迭代内的旧个体相比较，适应度值大的个体进入下次迭代.重复步骤4、5，对每个个体进行更新，使得整个种群进入下一代.

步骤7输出最优参数.

记录每一代适应度值，判断是否达到BSO算法最大迭代次数，直到算法终止，输出最优个体解Pbest.

步骤8PCNN网络参数的设置.

PCNN模型具有点火机制，神经元的状态会对邻域神经元产生作用，而点火阶段完全受到θ的影响.θ 如式（7）所示.

由于在传统PCNN模型中，脉冲门限具有非线性，本文通过ε 线性调节θ，每次得到θ后都减去ε ，从而影响脉冲产生.ε 如式（8）所示.

β控制邻域神经元的内部活动项强度，反映了当前像素与周围像素相互作用的范围，由式（9）确定.

式中：φ (I)为图像I归一化后的均方差.

衰减时间为

式中：∇I(x,y)为图像I在位置(x,y)处的梯度；W为链接权矩阵.

步骤9基于PCNN模型最佳参数的裂缝分割.

输入原始裂缝图像和PCNN模型参数，由脉冲输出矩阵Y记录点火情况，并判断是否达到PCNN模型最大迭代次数，若达到最大迭代次数，则输出最佳裂缝图像.

2 试验结果与分析

2.1 试验材料准备

本文提出的算法是针对不同环境下的路面裂缝图像分割的，选取的裂缝图像具有形态复杂、对比度差和噪声多的特点.

本文使用 2.40 GHz CPU和6.00 G RAM 的 Dell PC，MATLAB 2013编译环境进行仿真试验.

2.2 试验结果

首先将图像灰度化，统计裂缝图像的直方图信息，对PCNN中θ进行种群初始化，利用BSO算法进行聚类、替换、生成新个体、通过适应度计算个体熵值选择最优个体，BSO算法的参数优化测试结果如图1所示；每幅图像在很少的迭代次数之内均能达到最优解，虽然在最初的几代内最优解会出现微弱的波动，但在20代内基本达到一个恒定的值，收敛速度快；群体算法具有随机性，所以每幅图像的最差解会在最优解附近产生扰动，但整体不会偏差太多，从每幅图像的最优解和最差解对比来看，BSO算法较稳定，参数寻优能力强.同时结合图像自身特性和PCNN最大迭代次数，确定其他主要参数，将PCNN参数代到分割模型中迭代，由Y记录点火信息，并在PCNN模型迭代结束后，输出最佳裂缝图像，将其进行负变换，得到最终裂缝图像.

图1 BSO 参数优化曲线Fig.1 Curves of BSO parameter optimization

2.3 不同算法性能比较

对比度是图像分割中常用的指标，不同区域灰度大小的差异表现了目标与背景分割成不同区域效果的好坏，区域对比度如式（11）所示.

式中：uo、ub分别为目标区域（o）和背景区域（b）的平均灰度；Rτ为目标区域或背景区域；Sτ为分割区域τ内属于Rτ的像素数.

图像中的每个子区域具有相似的特征，子区域的一致性也能够体现分割效果的好坏，区域一致性如式（13）所示.

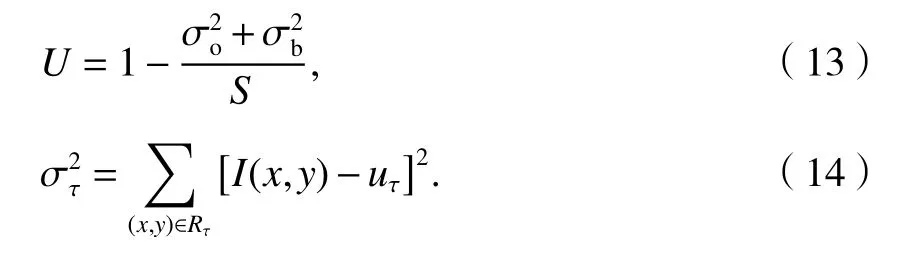
式中：στ2为区域τ的灰度方差；S为整幅图像的像素数.

算法运行时间反应了算法的效率，从而反映算法性能的好坏.分割后的图像与原始图像之间的信噪比（signal-to-noise ratio，SNR）反映了经过算法分割之后的图像质量.

为验证BSO-PCNN算法的性能和效果，将Sobel边缘检测算法、PCNN图像分割算法[5]（不包括形态学处理部分）、基于最大熵的遗传算法（genetic algorithm based on the maximun entropy of the histogram，GA-KSW）、基于遗传算法参数优化的PCNN 分割算法（genetic algorithm based on the pulse coupled neural network，GA-PCNN）[19]和 BSOPCNN算法进行对比，用不同形态、不同背景下的裂缝进行测试，效果如表1所示.

表1 不同算法对比试验Tab.1 Results Experiments of different algorithms comparison

不同算法的区域对比度和一致性对比结果如表2所示，算法运行时间和SNR对比结果如表3所示.

2.4 试验结果分析

由表1可知：Sobel边缘检测算法对于简单和复杂裂缝最大的问题就是噪声干扰大，裂缝边缘比较微弱，分割效果很差；PCNN算法虽然减少了单裂缝噪声，但是出现过分割现象，对于形态复杂的网状裂缝依然存在大量噪声造成欠分割；相较于前两种方法，GA-KSW分割后的裂缝图像噪声减弱；GAPCNN算法通过遗传算法寻优参数达到比较良好的裂缝分割效果，但依然有少量噪声存在，暗背景下的网状裂缝分割效果不明显；BSO-PCNN算法较GAPCNN算法而言，裂缝图像噪声更少，对不同类型图像分割都具有一定的适应性，不会出现过分割和欠分割的情况.

从表2可以看出：BSO-PCNN算法的平均区域对比度和区域一致性为0.090 0和0.992 4，要明显高于 Sobel算法的 0.039 7和0.991 7、PCNN 算法的 0.077 5和 0.992 0、GA-KSW 算法的 0.076 1 和0.992 3、GA-PCNN算法的 0.070 3和0.992 2，BSOPCNN算法对于不同背景环境下，不同形状复杂度下的裂缝图像都能达到比较理想的效果，裂缝轮廓边缘保留完整，在很大程度上明显削弱了噪声，裂缝整体更为突出.从表3看出：BSO-PCNN算法的分割时间为3.039 s，比 PCNN 算法的 7.479 s有明显的缩短，相较于PCNN算法前期的人工调参过程要节省大量时间.同时也要优于基于遗传算法优化的PCNN 算法的 3.265 s.与 Sobel、GA-KSW 算法相比，BSO-PCNN以时间复杂度换取了算法的有效性和准确性.BSO-PCNN算法和GA-PCNN的SNR都要高于Sobel、PCNN、GA-KSW的SNR.

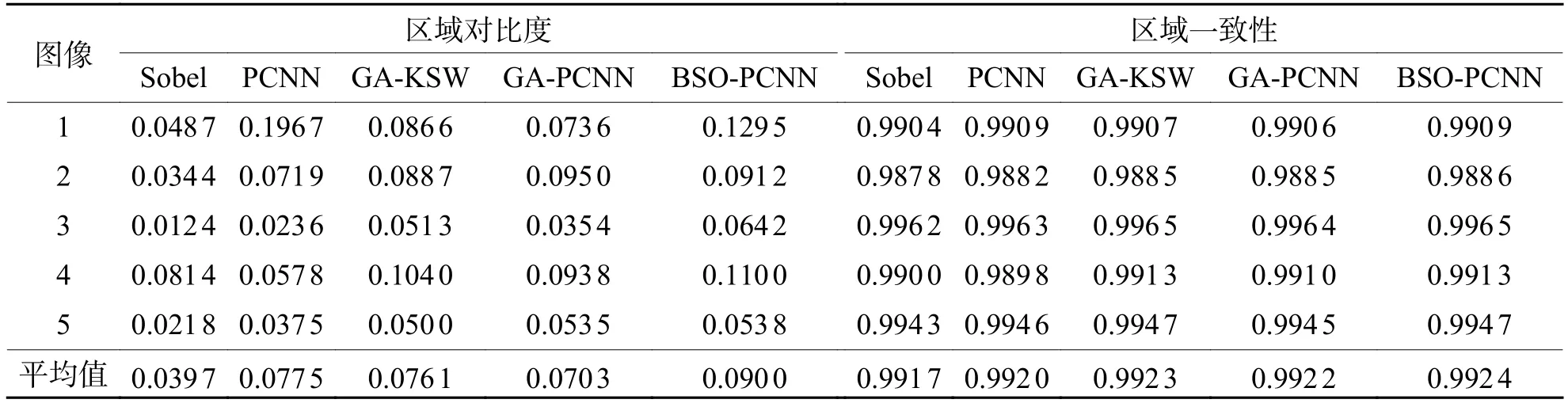
表2 不同算法的区域对比度和区域一致性Tab.2 Regional contrast and consistency of different algorithms

表3 算法时间和信噪比比较Tab.3 Comparison of algorithm time and signal-to-noise ratio

3 结 论

针对不同环境下不同形态的裂缝，本文提出了基于头脑风暴参数优化的PCNN裂缝分割算法.利用BSO算法解空间随机搜索能力强的特点，并结合图像自身特性自适应优化模型参数，较好地解决了人工调参的问题.BSO算法在3.039 s的迭代时间内就达到最大适应度值，找到最优参数，要远快于PCNN人工调参地时间.通过试验分析可知：BSO-PCNN算法的能有效改善PCNN算法的欠分割和过分割问题，较GA-PCNN算法而言，提取的裂缝轮廓更加清晰完整，且噪声少.性能指标中区域一致性、区域对比度都高于其他算法.但是对于一些形态复杂的裂缝分割，仍存在分割出的裂缝断裂的情况.