基于人工智能算法的隧道锚承载能力评价

王中豪 ，郭喜峰 ，杨星宇

（长江科学院重庆分院，重庆 400026）

随着我国道路基础建设的迅猛发展，跨越大江大河、深山峡谷的悬索桥被应用得越来越广泛，因造价优良、生态环保的显著优势，隧道锚这种锚碇结构形式也越来越多地应用到悬索桥的建设之中.悬索桥隧道锚方案首要探索的问题是稳定性评价，隧道锚稳定性的合理分析影响着经济建设和生命安全.

隧道锚稳定性分析主要为变形量和承载能力的分析，而张宜虎等[1]通过对10余个隧道锚专题研究统计发现，隧道锚在主缆数万吨级别荷载下的变形普遍为mm级，远远小于《公路悬索桥设计规范》（JTG/T D65-05—2015）[2]（以下简称《规范》）中对变形量的约束要求，控制隧道锚设计方案是否达标的主要问题是承载能力指标是否满足《规范》中要求的：锚塞体抗拔安全系数不应小于2.0，围岩稳定安全系数不应小于4.0.《规范》中对锚塞体抗拔安全系数给出了计算公式，将锚塞体看作重力式锚碇，采用重力锚抗滑稳定计算模式计算隧道锚抗拔安全系数，在操作上容易实现.而围岩稳定安全系数则由于隧道锚与围岩锚固受力体系的复杂性，隧道锚承载特性受围岩性质、锚塞体几何参数、锚塞体与围岩空间位置关系的影响，不同工程成果难以直接应用到下一个工程中，难以形成一个统一的解析计算方法和设计准则.《规范》中明确提出需要通过数值仿真模型确定围岩稳定安全系数，由于岩体力学参数的不易确定，甚至推荐较大比例的缩尺拉锚试验确定.

如邬爱清等[3]针对四渡河特大桥隧道锚的承载特性问题，采用了工程地质评价、室内及现场岩体力学试验、1∶12实体模型试验和有限差分数值模拟分析等岩石力学的综合研究方法，评价了隧道锚的变形和承载能力.张奇华等[4-5]在现场模型试验的基础上，结合数值分析，研究了普立特大桥隧道锚变形破坏过程，得到了隧道锚的超载稳定系数大于 8，并推导了假设圆台面破坏模式下的隧道锚抗拔力计算模式.李栋梁等[6]基于1∶10 的隧道锚原位缩尺模型试验，对太洪长江大桥隧道锚进行了承载特性的研究.胡波等[7]采用了现场模型试验和FLAC 3D数值模拟相结合进行对比研究的方法，研究了坝陵河大桥西锚碇的变形分布规律、破坏方式和承载最高应力.江南等[8]基于岩体弹脆塑性损伤本构模型，采用ABAQUS 有限元软件，针对丽江至香格里拉铁路云南金沙江大桥隧道锚进行稳定性分析计算，获得了隧道锚的承载能力，同时揭示了不同埋深情况下隧道式锚碇的破裂力学机制.

从上述可知，采用现场模型试验与数值模拟相结合的综合研究方法已成为每个隧道锚工程承载能力评价的标准配置.诚然，现场模型试验与数值模拟方法是对隧道锚设计方案的承载能力精确评价的可靠手段.但是现场模型试验是一个费时费力的工作，工程中往往是设计方案确定后，在施工的同时进行现场模型试验来对隧道锚设计方案进行验证.由于工程地质条件的复杂性、岩体力学参数的不确定性，数值模拟往往作为试验之后的辅助和补充.那么在反复调整的隧道锚初步设计阶段，如何设计出一个安全可靠、经济合理的隧道锚方案，设计者急需一种方法来对隧道锚承载能力做出评价，以验证初步设计方案的合理性.

岩体工程是一个定性、半定量的学科，重视工程经验的积累与类比.目前，随着近二十来年悬索桥的飞速发展，近二十余例隧道锚工程进行了以模型试验为主的专题研究，显然这些宝贵的工程案例为之后的隧道锚设计提供了丰富的经验来源.但影响隧道锚承载能力的因素很多，它们之间的耦合作用机制尚不明确，不同隧道锚的结构设计指标与工程地质、地形地貌差异性很大，难以找到两个条件相近的隧道锚，造成工程经验类比法使用起来障碍重重.而回避众多因素间相互作用的细观过程，从宏观上把控输入与输出关系的智能算法，为解决该类问题带来了新的思路.在21世纪，人工智能化高速发展、各种机器算法“百家争鸣”的今天，构建出一个既能学习这些宝贵的“大数据”又能预测新的隧道锚承载能力的非线性人工智能模型显然是具有可能性的.

1 承载能力影响因子及评价指标体系

隧道锚是一种楔形结构的特殊锚固体，悬索桥主缆荷载将主缆拉力传递到锚塞体混凝土，首先克服锚塞体混凝土的重力分量，然后再将剩余的荷载传递给周围岩体承担.与隧道锚相关的影响因素示意如图1所示.图中：A1为前锚面面积；A2为后锚面面积；L为锚塞体长度；γ 为扩散角；θ 为锚塞体倾角；E为岩体变形模量；F′为岩体抗剪断内摩擦系数；C′为岩体抗剪断黏聚力；H1为隧道锚的垂直埋深；H2为隧道锚距边坡地表的倾斜埋深.

图1 隧道锚相关影响因素示意Fig.1 Rlevant influencing factors of tunnel-type anchorage

显然，在混凝土设计密度较容易确定的情况下，锚塞体混凝土的体积大小决定了锚塞体混凝土承担的承载力份额，而A1、A2、L和 γ 则决定了其体积大小，同时锚塞体的空间布置形态（即锚塞体倾角θ）决定了重力在主缆拉力方向的贡献.

克服锚塞体重力分量后的剩余荷载经过复杂的锚/岩夹持效应传递过程，最终全部由岩体承担，本文不关心荷载如何传递的精细过程，仅着眼于如何从宏观上把握岩体承担荷载的能力大小和受哪些因素的影响.从内因上来说，岩体的质量越好，力学参数越高，岩体的承载能力就越强，在岩体工程计算中，常用变形模量E、岩体抗剪断强度（F′和C′）来表示.从外因上来说，首先岩体的力学特性受本身的应力场影响，隧道锚工程基本修建于埋深50～200 m左右的近浅部地下工程，应力场基本以自重应力场为主，因此可以用隧道锚的垂直埋深H1来表示自重应力的影响.其次由于隧道锚是埋设于边坡中的倾斜体，极限荷载下隧道锚的破坏轮廓基本以锚塞体中轴线为中心轴而沿边坡地表剪出，可见，隧道锚距边坡地表的倾斜埋深H2可代表岩体破坏后需要通过的路径大小.最后，由于隧道锚通常为两个，且分布的距离较近，两个隧道锚中间的岩体必然受应力叠加的影响，而考虑到同样的距离在不同的隧道锚会有不同的尺度效应，因此采用相对锚间距离S来量化，即双锚的中心轴距离与后锚面宽度的比值.对于单个隧道锚工程，理论上S为无穷大，但是为了计算的方便，取S=10.

综上所述，即可建立隧道锚承载能力Y与A1、A2、L、γ、θ、E、F′、C′、H1、H2和S影响因素指标体系的非线性映射函数关系，如式（1）.

根据隧道锚承载能力与影响因素指标的函数对应关系，收集张宜虎等[1]、王中豪等[9-10]、赵海斌等[11]和江南[12]文献资料中的工程案例信息，如表1所示，17个隧道锚工程同时涉及到软岩和硬岩，也同时包含了深埋和浅埋隧道锚.

表1 各隧道锚工程影响因素指标与承载能力汇总表Tab.1 Summary of influencing factors and bearing capacity of each tunnel-type anchorage project

2 最小二乘支持向量机

人工智能算法是一门多领域交叉的学科，亦能与岩体力学交叉、协调发展，并在解决很多岩体工程问题上提供了很好的途径，人工智能算法主要包括神经网络、专家系统、决策树、灰色系统和支持向量机等.结合本研究问题的特点和支持向量机的优良性能，本文采用最小二乘支持向量机构建非线性隧道锚承载能力评价映射模型.

1995年，Vapnik在统计学理论的基础上，基于结构风险最小化原理和Vapnik-Chervonenki维度概念，提出了支持向量机（support vector machines，SVM）这种新的机器学习方法，该方法引入了核函数，解决了在原空间上的非线性问题，有效避免了高维特征空间计算中的“维数灾难”，常用于解决模式识别、回归分析问题，特别是在解决小样本学习、非线性和高维的模式识别及回归分析问题中表现出显著的优势.在标准SVM的基础上，Suykens 采用了最小二乘线性系统误差平方和作为SVM的损失函数，扩展出了最小二乘支持向量机（least squares support vector machines，LSSVM）这种新的机器学习方法，从而将求解SVM 的凸二次规划问题转化成求解线性方程问题，大大降低了计算的复杂性，加快了求解速度.下面对LSSVM 非线性回归的原理作简要阐述.

假定有实数样本集(Xi,Yi)，其中：i=1,2,···,n，n为样本数；Xi∈Rm为m维系统输入向量；存在非线性映射函数 ϕ (•):Rm→Rmh将实现对m维输入向量映射至高维特征向量 Rmh；Yi∈R 为相应的一维输出值.对样本集可构造回归函数如式（2）.

最小二乘支持向量机优化问题的最小化函数为

式中：δ、ξi分别为惩罚系数和松弛变量.

函数的约束条件为

式中：ξ=(ξ1,ξ2,···,ξn)T.

引入Lagrange函数则变为

式中：α=(α1,α2,···,αn)T为Lagrange 乘子.

通过 Karush-Kuhn-Tucker条件获得参数 α 和b的最优值为

由式（6）得

将式（7）转换为矩阵方程，然后消去ω和ξ ，可得到等式方程为

式中：e=(1,1,···,1)T；I为n×n的单位矩阵；K为n×n的对称矩阵，其元素为满足Mercer条件的核函数，j=1,2,···,n.

当式（8）用核函数表示时，式（2）转化为

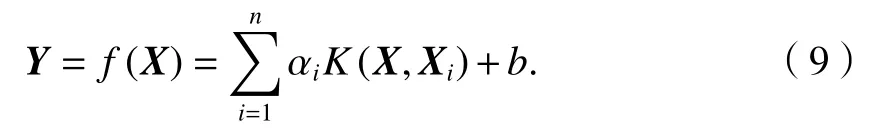
核函数K(X,Xi) 是将数据映射到高维空间增加线性学习器的计算能力，在计算和泛化性方面，核函数的使用都能够克服维数灾难.核函数是对称、连续、正定的函数.对于同样的问题，选择不一样的核函数会有不同的效果，目前，常用的核函数有多项式核函数、线性核函数、Sigmoid核函数和径向基核函数.考虑到径向基核函数具有较强的泛化能力和本研究问题的特点，因此本文以径向基函数作为核函数，径向基核函数的表示如式（10）.

式中：σ2为核函数参数.

因此LSSVM回归分析建模的质量的关键问题就转化为求解关键指标 σ2和δ.

3 粒子群优化算法

选定核函数的型式后，LSSVM模型结构即被确定，而核函数参数 σ2和惩罚系数 δ 的取值决定了LSSVM模型学习与预测性能的好坏.如何选取最佳组合( σ2, δ )是参数反演问题，需要在 σ2和δ的取值范围内进行若干次的赋值、运算、比较，才能确定出符合隧道锚承载能力评价模型的最佳组合( σ2, δ ).为了提高多次迭代的计算效率，目前常用遗传算法、粒子群算法、蚁群算法等优化算法进行处理.本文采用粒子群算法，郑志成等[13]用该算法与LSSVM完美地组合并有效解决了岩土工程问题.

粒子群算法中将求解任意一个最优问题类比为寻找所有粒子群中唯一的最优粒子.通过制定的优化函数，获得全部粒子的速度方向与距离，然后比选出最优粒子的方向，其它的粒子再跟随当前的最优粒子在解空间中继续搜索迭代，直到找到最优的解决方案.粒子群群体中经过多次的迭代计算后，会不断更新两个极值.一是在每次搜索中单个粒子的最好值，称为单体极值Pbest，其次为整个粒子群在每次搜索中所达到的最好值，称为全局极值gbest.

假设粒子群中，粒子i在解空间的位置为ui=(ui1,ui2,···,uin)，它的速度为vi=(vi1,vi2,···,vin) ，第i个粒子的个体极值为Pbest,i=(Pi1,Pi2,···,Pin) ，粒子群的全局极值为gbest=(g1,g2,···,gn).每次迭代得到Pbest,i与gbest后，用式（11）、（12）更新其速度和位置.

式中：µ1和 µ2为学习参数，在(0,2)范围内取值；r1和r2为随机数量，在(0,1)范围内取值；ψ 为动量参数，量值随迭代计算而变化；k为当前迭代次数.

4 LSSVM承载能力评价模型的学习

在MATLAB上进行模型的学习训练，根据经验，设置 σ2的取值范围为[1,5]，δ 取值范围为[100,500]，设定粒子群规模为20，首先在 σ2和δ 取值空间内随机产生一组( σ2, δ )作为粒子的初始位置，然后通过LSSVM工具箱中的trainlssvm函数，对表1中的输入样本进行拟合，并不断迭代计算、比较选择最优的粒子，经过100次的迭代得到 σ2为500、δ为1最优.由于隧道锚工程样本数量较少，将训练样本同时作为检验样本，使用simlssvm函数和该组参数对训练样本进行计算，得到承载能力预测值，并与试验值进行对比，如图2所示.从图中可知，预测值与试验值几乎重合，该模型的学习效果较好.

图2 输入样本中预测承载力与试验承载力对比Fig.2 Comparison of predicted bearing capacity and test one for input samples

5 工程应用

某大桥隧道锚单锚主缆设计荷载为130 MN，隧道锚洞斜长70 m，锚塞体最大埋深约50 m，双锚主缆中心距在IP 点处为33.365 m，锚塞体纵断面设计为前小后大的楔形体，锚塞体斜长40 m，与水平线的倾角为45°.锚塞体横断面采用城门洞形，顶部为半圆弧形，侧面和底部为直线形.前锚面顶部圆弧半径5.2 m，侧面边墙高5.2 m，底部宽10.4 m.后锚面顶部圆弧半径7.5 m，侧面边墙高7.5 m，底部宽15.0 m.该隧道锚的基岩以中风化较完整石英长石砂岩为主，经现场岩体力学试验获得成果如表2所示（表中F为抗剪强度内摩擦系数）.

表2 基岩物理力学参数Tab.2 Physical and mechanical parameters of surrounding rock

由前文可知，前锚面面积A1为96.5 m2、后锚面面积A2为200.8 m2、锚塞体长度L为40.0 m、扩散角 γ 为3°、锚体倾角 θ 为45°、变形模量E取 3 GPa、内摩擦系数F′ 取 0.73、黏聚力C′ 取 3.5 MPa、垂直埋深H1为45.0 m、倾斜埋深H2为64.0 m、相对锚间距离S为2.230.通过前述学习好的LSSVM承载能力评价模型进行预测计算，得到该隧道锚的承载能力为1 324.7 MN，将该预测承载能力与单锚主缆设计荷载进行比值即得到该隧道锚的承载能力为10.2P（1P表示1倍设计荷载）.

后期对该大桥隧道锚工程进行了现场1∶10缩尺模型锚试验，模型逐级加载到16.5P，地表开始出现第1条可见裂缝，继续逐级加载到18.0P后，地表的裂缝陆续增加至13条，压力不在继续增大，变形持续增长.通过对不同加载量与锚塞体变形的关系曲线进行分析，如图3所示.模型锚在4.0P荷载以下，锚体位移近乎线性增长，荷载 ＞ 4.0P后，变形速率增长，曲线向下凹，因此4.0P为比例极限强度，到11.0P时曲线出现拐点，位移随着荷载级数的增长而明显地增大变形速率，因此11.0P为屈服强度，而加载极限值18.0P为峰值强度.

图3 模型试验锚塞体荷载-变形曲线Fig.3 Load-deformation curves of anchoring concrete-plug in model test

于此同时，基于FLAC3D有限差分程序，对该隧道锚进行了弹塑性数值分析，采用超载法施加应力，监测锚塞体在各级荷载下的变形如图4所示.锚塞体的荷载变形曲线在11.0P呈现出明显的拐点，在 ＜ 11.0P时，变形基本呈线性增加，且增加缓慢，之后变形增加速率明显加快，表明超过11.0P后整个隧道锚系统处于塑性屈服破坏，即11.0P为该隧道锚的承载力.

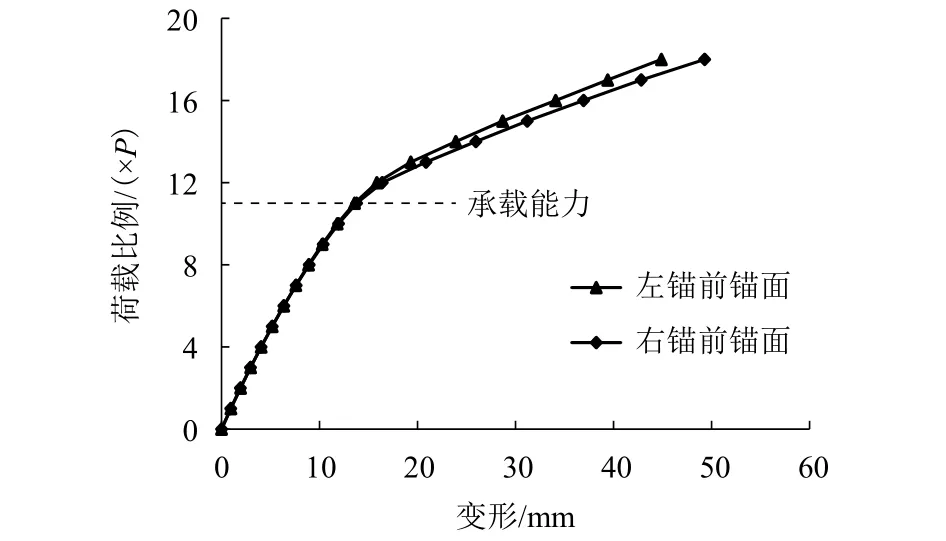
图4 数值模拟锚塞体荷载-变形曲线Fig.4 Load-deformation curves of anchoring concrete-plug by numerical simulation

该桥隧道锚综合现场1∶10缩尺模型锚试验和数值模拟专项论证后确定该隧道锚的承载能力为11.0P.上述结果表明，基于LSSVM承载能力评价模型预测的隧道锚承载能力10.2P与专项论证结果基本相近，表明用该方法进行预测是可行的，效果较为理想.同时预测结果略小于专项论证结果，主要是由于该模型的学习样本中，一些工程案例在无法得到承载能力真值的情况下，取用了低值，如泸定大渡河特大桥隧道锚现场模型试验由于施力系统的加载能力限制，最大只加载到7.8P，实际上还未达到它的承载极限，但对输入样本中以7.8P作为该隧道锚的承载能力，因此该模型的预测结果是偏于保守的.

6 结 论

1）基于隧道锚受力机制的分析，确立了前锚面面积、后锚面面积、锚塞体长度、扩散角、锚体倾角、变形模量、岩体抗剪断内摩擦系数和黏聚力、垂直埋深、倾斜埋深和相对锚间距离共同影响隧道锚承载能力的评价指标体系.

2）构建了PSO-LSSVM隧道锚承载能力评价模型，通过搜集到的17个隧道锚工程案例作为训练样本，取得了不错的学习效果.

3）将训练后的PSO-LSSVM模型预测某大桥隧道锚承载能力，通过与隧道锚现场缩尺模型试验和数值模拟方法获得的结果比较，其结果几乎一致，表明该模型的预测效果较为理想，对工程具有一定的指导意义.

4）本文的研究为解决隧道锚承载能力评价提供了新的途径，但还需积累更多的案例，不断扩充学习样本，向真正的“大数据”方向靠拢，从而建立吸收了更多工程经验、“越学越聪明”且适用各类工程地质条件的LSSVM模型，为新设计的隧道锚提供更准确的承载能力评价.