基于综合指数法的无砟轨道配筋方案检算与分析

高 亮 ，赵闻强 ，钟阳龙 ，仝凤壮

（北京交通大学土木建筑工程学院，北京 100044）

无砟轨道具有高平顺、高稳定、高可靠性等优势，在我国高速铁路和城市轨道交通线路得到了广泛的应用[1].无砟轨道是典型的钢筋混凝土结构，从结构及功能上，基本可将配置的钢筋分为轨道板普通钢筋、轨道板预应力筋、底座板钢筋及一些特殊的钢筋.例如以中国高速铁路无砟轨道系统（CRTS）为例，轨道板/道床板配有一定数量的普通钢筋，而在一些预制轨道板结构还额外配备了预应力筋对轨道板施加了预应力效应以改善其服役性能；除部分路基、隧道内结构采用素混凝土和HGT水硬性支承层外，在CRTSⅡ型、CRTSⅢ型板式无砟轨道底座板内均配置了钢筋骨架；CRTSⅢ型板式无砟轨道还设置了门型筋、自密实混凝土整体配筋及凹槽加强配筋等特殊钢筋以保证其特殊的功能定位[2].

目前国内外针对无砟轨道结构的配筋设计主流方法主要可分为容许应力法与极限状态法，并在设计后利用相关公式对强度及裂缝宽度进行检算.日本无砟轨道主要采用了容许应力法进行配筋设计，在严寒地区引入部分限界状态设计法的预应力结构；欧美地区则以极限状态设计法作为主流；我国主要采用了容许应力法设计[3]，但也有学者采用极限状态法对CRTSⅢ型板式无砟轨道进行了配筋设计[4-5].针对内部钢筋配置形式的研究，国内外学者已有一定的研究，其中很大一部分集中在由连续配筋混凝土路面（CRCP）发展而来的双块式无砟轨道（CRCT）上：王森荣[6]基于对双块式无砟轨道与配筋混凝土路面结构的对比分析，提出了我国双块式无砟轨道的道床板配筋要求；Cho等[7]针对配筋率对双块式无砟轨道拉应力、裂缝宽度等性能的影响初步探讨了改变钢筋位置对无砟轨道力学特性的影响；赵坪锐等[8-9]针对双块式无砟轨道连续道床板开展混凝土开裂特性模型试验；任娟娟等[10-11]则计算了配筋对连续道床板裂纹的影响.此外，部分学者还对内部钢筋失效、破坏后轨道结构受力性能进行了评估：赵磊等[12]对CRTSⅠ型板式无砟轨道部分预应力破坏后导致的附加荷载影响进行了分析，研究了不同位置、数量预应力筋破坏对轨道板附加荷载的影响；徐家铎[13]对CRTSⅠ型板式无砟轨道预应力筋锚穴附近混凝土损伤进行分析.

综合来看，现有无砟轨道配筋设计检算方法仍主要集中于基于平截面假定的容许应力法或极限状态法，设计后通过相关公式对材料强度及裂缝宽度进行检算.按照传统设计理念检算时结构内钢筋配筋率、特殊钢筋数量等指标合格即检算完成，对其结构及部件配筋后内部受力变形协调性等情况关注不多；对于钢筋布置方式的研究也大多集中于无砟轨道配筋率改变及预应力钢筋出现破坏时对无砟轨道对结构变形、应力的影响，少见针对无砟轨道内部钢筋具体排布方式对其服役特性的研究.

基于此，本文借鉴综合指数法构造了无砟轨道配筋检算指标，并以无砟轨道板内部配筋为例，通过有限元方法建立了无砟轨道配筋检算分析模型，研究了无砟轨道板内部钢筋具体排布方式对无砟轨道服役性能的影响.其主要目的在于弥补既有配筋方法在钢筋布置优化方面的局限，将配筋方案向可视、可调、精细化设计的方向发展.期望通过该方法的研究，只需在结构内力计算的基础上对结构配筋进行细微调整，达到改善、均衡局部应力应变状态的目的，从而进一步增强结构长期服役性能.

1 基于综合指数法的配筋检算指标构造

配筋方案的优劣在一定程度上影响了轨道板适应运营环境的能力.目前对轨道结构配筋表现进行评价时，大多采用了应力在某一路径的直观分布并比较其拉应力峰值，通用性不强，无法完全说明配筋方案改变带来的受力差异对整体服役性能的影响，对结构内部的受力变形均衡性也关注不够.为系统考虑结构相应特征，借鉴水质评价领域常用的综合指数法，结合无砟轨道结构特点，提出能够反映配筋后结构内部应力均衡、变形协调的配筋检算指标.

1.1 基于综合指数法思想的配筋指标构造流程

综合指数法具有综合性强及可比性高等特点[14]，本文基于其基本思想构造配筋检算指标，主要流程如图1所示.

图1 配筋检算指标构造流程Fig.1 Construction process of reinforcement check index

构造合理的配筋指标后，考虑到无砟轨道作为典型的板结构，在进行整体状态评价时，从空间分析的角度将轨道板沿厚度方向分为多层，获取单个指标的分量数据分布图层X1与X2，以此避开原有的峰值、路径评价方法在表征整体均衡性上的局限.确定权重因子后对各分量叠加运算，最终通过统计指标进行量化评价.

上述流程将应力均衡、变形协调特性分别独立，并通过数据的正则化/标准化避免了数据符号的影响，又通过空间分析（图层）以保证数据的连续性，使得原本的配筋后结构整体方案评价问题最终转换为构造合适的正则化特征分量的问题.

1.2 整体应力变形水平特征分量的选择

考虑到外力在变形过程中所做的功将全部转化为内能储存在弹性体内部，因此结构受力后的应变能增量为表征结构应力特征提供了一个合理的思路.参考第四强度理论中主要将形状改变能密度作为材料发生塑性屈服破坏的依据，即达到单向拉伸时发生塑性屈服破坏的形状改变能密度时，结构发生塑性屈服破坏[15]，本文也只考虑形状改变能密度作为结构应力特征的表征指标.

在应变能密度中，对应的形状改变能密度为

式中：σ1、σ2、σ3分别为结构的 3 个主应力；E为弹性模量；v为泊松比.

根据材料力学的概念，式（1）也可写为

式中：σx、σy、σz分别为结构三向正应力；τxy、τyz、τxz分别为结构三向 切应力；σS为结 构von-Mises应力.

由式（2）可知，Vd综合了结构各方向正、切应力及位移变化矢量，可作为结构整体应力特征分量X1.

1.3 受力变形均衡性特征分量的选取

在明确受力变形空间分布的基础上，评价其均衡协调性宜采用相对量，而无砟轨道受力变形分布从几何要素上可视为多个三维欧氏空间中的曲面.曲面上反映出的相对量特征可为本文寻求均衡性特征分量X2提供一定参考.

曲面曲率在一定程度上反映了曲面的质量，在各个曲率指标中，高斯曲率实际反映曲面的弯曲程度，当高斯曲率发生突变时，即发生曲率不连续时，结构已存在开裂等不连续问题.根据前期研究，轨道板受力变形分布不易出现反弯特征，也规避了高斯曲率为负的条件.本文选取高斯曲率作为结构均衡性分量的表征指标X2.当曲面表达为式（3）时，

高斯曲率K则为

图2为某一层面产生变形后的位移分布及相对应的高斯曲率，由图2可以很清晰地看出高斯曲率所代表的物理意义.

图2 层面变形与高斯曲率分布Fig.2 Deformation and Gaussian curvature of structure layer

1.4 叠加计算及整体均衡性指标量化

在综合指数法的具体实施过程中，将无砟轨道板结合单元划分情况沿厚度方向划分为多个图层，于各层节点提取各点处形状改变能密度及变形后高斯曲率.从物理意义上，形状改变能密度中已包含了应力分量与位移矢量，此处曲面曲率的作用则是引入均衡性评判指标，即相当于通过定量评价位移变量的挠曲程度，将变形均衡系数引入应力特征分量中，因此确定其权重比为1∶1，并根据其正相关关系进行点乘得到最终整体图层结构面某一点的结构受力变形综合指数为

为了量化各方案间受力变形差异，借鉴轨道不平顺评价指标中幅值管理及轨道质量指数（track quality index，TQI）的理念，选取结构各图层结构受力变形综合指数峰值及均方差进行对比，为消除由量纲和数据尺度带来的影响，进一步提取变异系数进行对比.变异系数定义为标准差σ与平均值μ之比，即

2 无砟轨道配筋检算分析模型

本文以CRTSⅢ型普通板式无砟轨道为例，应用文章提出的配筋评价指标，分析无砟轨道板内部钢筋排布方式对其受力特性的影响.

2.1 无砟轨道数值仿真模型的建立

CRTSⅢ型普通板式无砟轨道自上而下分别由轨道板、自密实混凝土、底座板组成，但考虑经济性取消了轨道板内双向预应力筋.

钢轨为CHN60轨，采用梁单元模拟；扣件采用多根三向弹簧-阻尼单元模拟，扣件间距为0.63 m，垂向静刚度为45 kN/mm，横向静刚度为50 kN/mm，最大纵向阻力9 kN/组.

采用实体单元对轨道结构主体建模，轨道板采用C60混凝土，标准轨道板长5.6 m，宽度为2.5 m，厚度 0.2 m.自密实混凝土层厚度为0.09 m，宽度与轨道板相同；底座采用C40混凝土，宽度为2.8 m，厚度为0.3 m，底座上设置2 个尺寸为600 mm × 600 mm ×100 mm的凹槽，每块底座板上设置3块轨道板，轨道板间保有一定长度的伸缩缝[16].

本文采用桁架单元模拟轨道板纵、横向主筋，认为其预制施工后钢筋与混凝土间粘结良好，为计算便利，模拟钢筋与轨道板单元相互作用时将钢筋单元嵌入至轨道板单元内.模拟轨道板与自密实混凝土层间关系时，考虑门型筋对层间粘结作用的补强，将两者共节点建模；对自密实混凝土与底座间的隔离层，将其模拟为法向可分离，切向存在一定摩擦的“硬接触”行为；底座凹槽四周配备有缓冲垫层，模拟时将其定义为一定的接触刚度；下部基础采用路基弹簧进行简化模拟，建模具体材料参数如表1所示[17].

表1 数值仿真模型材料参数Tab.1 Material parameters of numerical model

为消除边界效应，模型计算长度取三块底座板长度，并以中间底座板的正中轨道板作为分析对象，所建立的无砟轨道配筋检算模型如图3所示.

图3 CRTSⅢ型普通板式无砟轨道配筋检算模型Fig.3 Reinforcement checking calculation model of CRTS Ⅲ ordinary steel type slab track

2.2 配筋工况设计

依据相应荷载下结构内力，采用传统的配筋设计方式对该无砟轨道板进行钢筋配置方案的初步设计.设计结果表明，为满足配筋率要求，横向钢筋面积应不小于 4720.1 mm2，纵向配置钢筋面积应不小于3618.3 mm2.为了保证钢筋骨架的成型，将横、纵向钢筋按两排进行布置，在保证构造要求及保护层厚度的前提下，选用多种直径及数量的钢筋进行配筋方案的具体设计.

在设计不同轨道板钢筋排布方式时，以相同配筋率为基本设计原则，考虑实际施工、绝缘等要求，选取了ϕ12～ϕ16的HPB300钢筋进行排布.首先配置了整体较为稀疏、钢筋直径较大的方案1；减小钢筋直径，增加了钢筋数量将钢筋尽量满布至轨道板内，并在轨下位置适当加密，以此设置了方案2；之后考虑车辆荷载下弯矩分布在轨道板内对应承荷位置钢筋间距进一步加密，基于此对方案2 进行调整设置了方案3（为保证骨料咬合最密间距为两倍保护层厚度），具体方案情况如表2所示，各方案横纵向钢筋在轨道板内部的具体位置采用红色线条表征，见表3.

表2 保证相同配筋率条件下不同普通钢筋配置方案Tab.2 Different reinforcement arrangement scheme under same reinforcement ratio

表3 横纵向钢筋在轨道板内部的具体位置Tab.3 Specific position of transverse and longitudinal reinforcement inside the rail plate

在检算过程中，考虑到不同方案在不同荷载下表现有所区别，本文以无砟轨道服役时所受长期荷载内较为典型的车辆荷载与温度荷载为例，对其荷载效应影响下的轨道板服役状态进行分析.其中车辆垂向荷载以CRH3型车为例，根据《高速铁路设计规范》[18]取为三倍静轮重225 kN，温度荷载取整体升温 45 ℃、整体降温 40 ℃、正温度梯度 90 ℃/m及负温度梯度45 ℃/m，温度梯度单独加载轨道板.

3 不同钢筋配置方案检算分析

3.1 车辆荷载下不同方案表现分析

首先对综合指数作评价指标的效果进行验证.以车辆荷载作用下方案1为例，施加垂向车辆荷载后，提取轨道板板底纵向应力、垂向变形以及板底、板顶受力变形综合指数分布如图4（a）～（d）所示.

由图4可知，在分布形式上，相较于传统的纵向应力、垂向位移指标，综合指数峰值主要集中分布于直接承受车辆荷载的扣件位置，更能集中反映出轨道板整体的不均衡点（此处为扣件支承效应）.

图4 车辆荷载作用下轨道板典型力学指标分布（方案1）Fig.4 Distribution of typical mechanical indexes of track slab under vehicle load (scheme 1)

为定量比较综合指数指标对差异率的贡献，提取不同力学指标的统计值如表4所示.

表4 车辆荷载作用下不同普通钢筋配置方案下板底指标对比Tab.4 Comparison of statistical indexes of bottom of track slab for each scheme under vehicle load

由表4可知：3个方案在各指标上均有不同程度的差异；以量值差异较大的方案1与方案3为例，方案3在纵向应力、垂向位移的峰值较方案1分别下降了8.3%和6.1%，而在综合指数峰值上差异率达到了16.3%；在均方差与变异系数指标上，两方案的综合指数也较传统指标差异更大.

即使在荷载经过传递更为分散的轨道板底，综合指数较传统指标也体现出更大的差异率，说明本文提出的综合指数在局部配筋细微调整评价方面效果更好，对钢筋排布方案的检算更具适应性.

本文在空间分析时将轨道板依据网格情况沿厚度方向分为多个图层，以板宽与板长方向作为图层的基本坐标系.由图4（c）和图4（d）可知：不同于有砟道床的散体结构，轨道板的相同坐标节点在厚度方向各指标变化呈现出连续性，即只需通过提取顶面与底面图层来综合评价结构配筋后整体表现.

为更全面地评价3种方案在受力均衡性上的优劣，进一步提取分布较为集中的板顶综合指数统计指标量值如表5所示.

相对其他层面，顶面综合指数指标量值最大，且差异更为显著，由表5可知：方案1相对方案2在各指标上均有不同程度地增加；方案1综合指数峰值与均方差较方案2增加了20.5%，说明此时方案1的均衡性表现更差；方案3较方案2在综合指数峰值、均方差、变异系数指标上均有减小，说明此配筋方案在钢轨轨下位置确实对轨道承载刚度有一定程度的加强.

表5 车辆荷载作用下不同普通钢筋配置方案下板顶各综合指数指标对比Tab.5 Comparison of statistical indexes of track slab top for each scheme under vehicle load

综合车辆荷载作用下各配筋方案表现，可认为方案3表现最佳，方案2次之，方案1表现最差.

3.2 整体升温荷载下不同方案表现分析

以整体升温作用下方案1为例，对轨道结构施加整体升温45 ℃后，提取轨道板板顶及板底的受力变形综合指数分布如图5（a）、（b）所示.

由图5（c）、（d）可知，在整体升温荷载作用下轨道板热胀变形受到了来自上部扣件的约束作用，轨道板板顶能够看出明显的扣件支承约束效应.轨道板综合指数峰值均出现在轨下板端位置处.提取各方案轨道板顶、板底受力变形综合指数的各统计量进行横向对比如表6所示.

图5 整体升温下轨道板板顶、底综合指数分布Fig.5 Comprehensive index distribution of top and bottom of track slab under overall temperature rising load

表6 整体升温作用下不同普通钢筋配置方案板顶、底各综合指数指标对比Tab.6 Comparison of comprehensive statistical indexes of different schemes under overall temperature rising load

由表6可知：综合对比3种配筋方案轨道板受力变形情况，从方案1到方案3，各综合指数统计指标均有不同程度的变化；其中方案2在轨道板顶面与底面综合指数峰值上分别较方案1减小了13.58%和34.67%；但方案3轨道板顶面在综合指数峰值方面较方案1增大了一倍有余.对比各方案综合指数的均方差与变异系数也能发现类似的规律.

对比图5后发现：方案1与方案3轨道板受力变形综合指数分布相似，两方案在板中等大部分位置量值也基本接近，只在峰值处（即轨下板端位置）有非常明显的区别，说明此时方案3在轨道板端部受力更不均衡.这也解释了方案3与方案1的变异系数与标准差存在较大差异的现象.

提取各方案钢筋von-Mises应力分布云图进行对比，如图6.

由图6可知：3种方案钢筋von-Mises应力峰值差异不大，且均远远小于300 MPa的限值，说明此时3种方案的钢筋都处于正常工作范畴；相较于方案1与方案2，方案3在集中布置的纵向主筋端部的von-Mises应力分布更大，集中布置钢筋后，此处钢筋温度力增加明显，并集中传递至轨道板混凝土端部.很好地解释了方案3轨道板的综合指数在端部较方案1与方案2有显著增加的现象.

图6 整体升温时各方案钢筋 von-Mises应力分布Fig.6 von-Mises stress distribution of reinforcement of different schemes under overall temperature rising load

综合对比3种配筋方案在整体升温荷载下的表现可知：方案2要优于配筋数量较少、钢筋直径更大的方案1；由方案3结果可以发现，在对应轨下位置集中配置纵筋后，该处由钢筋温度力集中于端部区域，使得轨道板端部受力增加；尽管钢筋与混凝土的温度线膨胀系数相近，当温度变化时，二者之间不会产生较大的相对变形，但此时端部集中的配筋仍然导致轨道板受力更不均衡.

对整体降温荷载下3种配筋方案进行分析也可得出类似的规律，限于篇幅，在此不再赘述.

3.3 正负温度梯度下不同方案表现分析

对轨道板施加正温度梯度90 ℃/m与负温度梯度45 ℃/m后，提取各方案轨道板顶、板底受力变形综合指数的各统计量如表7所示.

由表7可知：正温度梯度作用下，3种方案在顶面综合指数上的差异较小，各统计指标主要差别集中在底面；对比底面各指标可知，方案2较方案1在综合指数峰值上减小了11.97%，综合指数均方差减小了8.4%，变异系数减小了14.4%；此时方案2轨道板受力更为均匀，说明此时方案2轨道板受力更为均匀；方案2与方案3基本一致，与方案1存在差异；负温度梯度作用下各方案综合指数统计指标无明显差异.

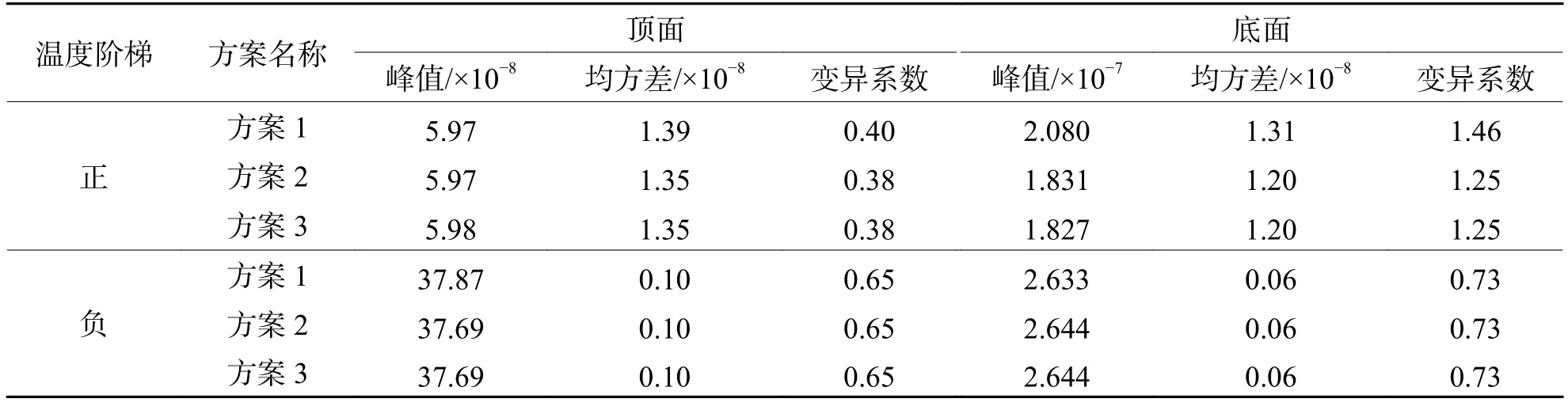
表7 正、负温度梯度作用下不同普通钢筋配置方案综合指数指标Tab.7 Comprehensive index of different reinforcement schemes under positive and negative temperature gradients

综合本文3种方案在不同荷载下的检算结果，由上述一系列定性、定量分析，以方案2为基准，将不同方案进行比较如表8所示.

表8 不同荷载作用下各方案综合比较（以方案2为参照）Tab.8 Comparison of different schemes under different loads (referring to scheme 2)

由表8可知：除了车辆荷载作用下方案3较方案1、2服役性能略有提升，综合其余工况，方案2要明显好于方案1、方案3；方案1配筋数量较少，配筋方式过于分散，在承受不同荷载时其表现较其余两方案更差；方案3中过于集中的配筋在加强结构局部刚度的同时反而破坏了原有的协调性，可能会在承受复杂温度荷载时带来新的问题，此外，在局部过于集中的配筋还有可能导致局部的超筋破坏风险，并对施工造成影响.因此，钢筋排列密布且轨下适度加密排布的方案2对复杂服役环境环境适应性更强，其布置方案较为合理.

4 结 论

本文基于综合指数法构造了无砟轨道结构配筋检算指标，并通过有限元方法建立了无砟轨道配筋检算分析模型，研究了钢筋排布方式对无砟轨道力学性能的影响，主要结论如下：

1）在配筋检算时，可将结构的形状改变能密度与曲面高斯曲率基于综合指数法思想结合，以评价结构配筋后应力、变形均衡性.

2）相较传统应力指标变形，本文提出的综合指数在分布上能更好地突出不均匀区域；在量化方案评价时指标间具有更大的差异率，在评价调整配筋方案时更具适用性.

3）在满足配筋率的前提下于轨下位置额外密布钢筋，能够在一定程度上增强刚度，提升轨道板抵抗垂向车辆荷载的能力.

4）轨下位置过于集中的配筋在加强结构局部刚度的同时反而破坏了整体的均匀性，尤其在整体升降温荷载下轨道板端部综合指数明显升高，较均匀密布工况增大了近1倍.

综合来看，满足配筋率与构造要求的情况下，选择钢筋直径较小、排列更为密布的钢筋方案并在轨下位置适度加密，更能够改善轨道板在不同环境下的受力状态，使其在控制裂纹、结构耐久性上能够保持更为优越的长期服役性能.本文关注了轨道结构受力的均衡性特征并对在评估方法方面进行了一定的尝试，未来还可结合进一步的理论研究，提出更为完善的均衡性评估指标.