薄壁箱梁挠度的一种简化分析方法

周茂定 ，蔺鹏臻 ，张元海 ，冀 伟

（1.兰州交通大学土木工程学院，甘肃 兰州 730070；2.甘肃农业大学水利水电学院，甘肃 兰州 730070）

薄壁箱梁因其具有较好的力学特性而被广泛应用.随着我国桥梁建设步伐的加快，有关在役箱梁桥出现不同程度开裂下挠的报道[1-2]也逐渐增多.对此学者从设计、施工等方面进行了深入研究，结果表明剪切和徐变变形是造成箱梁持续下挠的重要原因[3]，因此剪切变形对薄壁箱梁挠度的影响将不容忽视.同时，随着新型轻质高强混凝土的逐步应用，现代箱形梁截面不断向着薄壁轻型化方向发展[4]，剪切变形对箱梁挠度的影响将更加凸显.近年来，研究发现箱梁翼板面内剪切变形（即箱梁剪力滞效应）对箱梁挠度有重要影响[5-6].我国现行公路桥梁规范[7]给出了剪力滞的简单计算方法，却未给出挠度对应的计算方法.对此，蔺鹏臻等[8]利用规范剪力滞的方式修正计算翼板剪切引起的箱梁挠度.目前，在求解箱梁剪力滞效应产生的附加挠度时必须进行剪力滞效应分析[5-6，8]，因而导致分析复杂.对箱梁腹板剪切变形的分析，文献[9-11]通过给腹板引入不同的挠曲转角函数分析其对箱梁挠度的影响.当采用能量变分法求解时，由于涉及多个未知挠曲转角函数，使得求解分析过程十分复杂.综上所述，以上求解箱梁挠度的方法均需分析薄壁箱梁的剪力滞效应，同时所涉及的未知函数较多，分析过程相对复杂.文献[12]虽将翼板与腹板剪切变形综合为一个未知函数来分析，但截面参数等求解复杂，不便于实际工程应用.因此，寻求一种简便适用的薄壁箱梁挠度计算方法就很有必要.

本文将利用材料力学中的单位力法及虚功原理对考虑全截面剪切影响的薄壁箱梁挠度展开研究，并基于Timshenko梁理论提出薄壁箱梁挠度求解的简化方法.

1 简单箱梁结构的挠度分析

以承受任意分布荷载p(z) 的悬臂箱梁为分析对象，采用正交笛卡尔坐标系O-xyz，如图1所示.图中：ht、hb分别为形心轴x与顶板、底板中心处的垂直距离；h为梁高；b1、b2和b3分别为箱梁顶板、底板的一半宽度和单侧悬臂板宽度；P0为梁端的单位荷载.

材料力学中常采用单位力法求解上述悬臂梁的挠度[13].对于图1 所示箱梁，假设P0=1，单位荷载产生的总外功为[13]

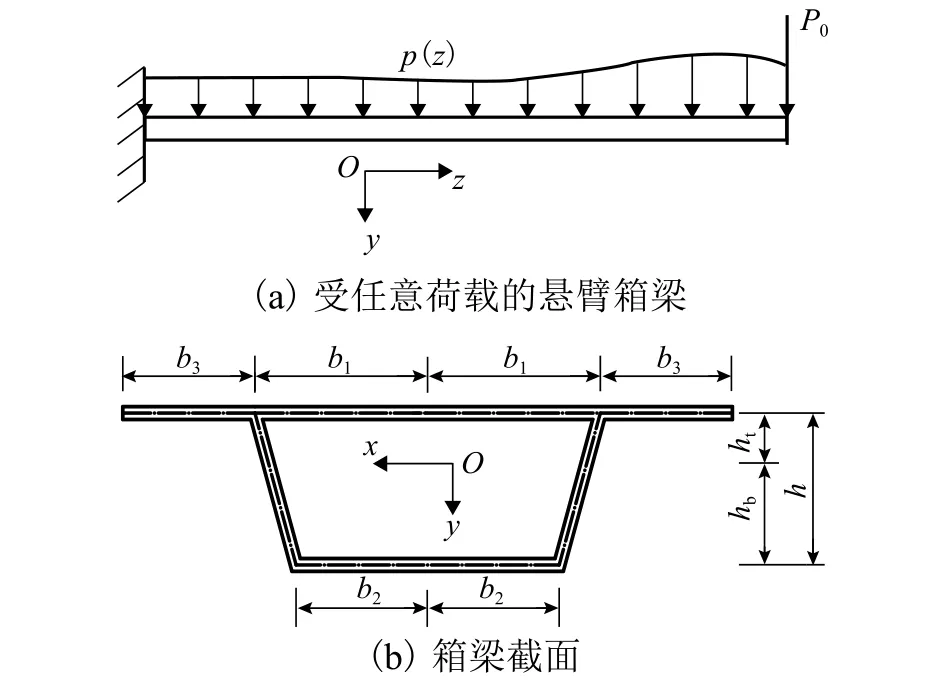
图1 悬臂箱梁示意Fig.1 Schematic of cantilever box girder

式中：Δ为广义位移，在此可认为是悬臂梁的挠度.

悬臂梁的内虚功是当箱梁的应力（由单位荷载引起）在实际荷载产生的变形上所做的功.单位荷载作用于上述箱梁结构引起的内力为弯矩M0和剪力Q0.设s为沿箱壁中心周线的流动坐标，从箱梁截面中取出任意 ds× dz的微元板，如图2 所示.图中：t为壁厚；σ为在此微元上产生的正应力；τ为剪应力；ε和γ分别为正应变和剪应变.应力、应变如式（2）～（5）所示.

图2 微元板虚功分析Fig.2 Virtual work analysis of micro-element

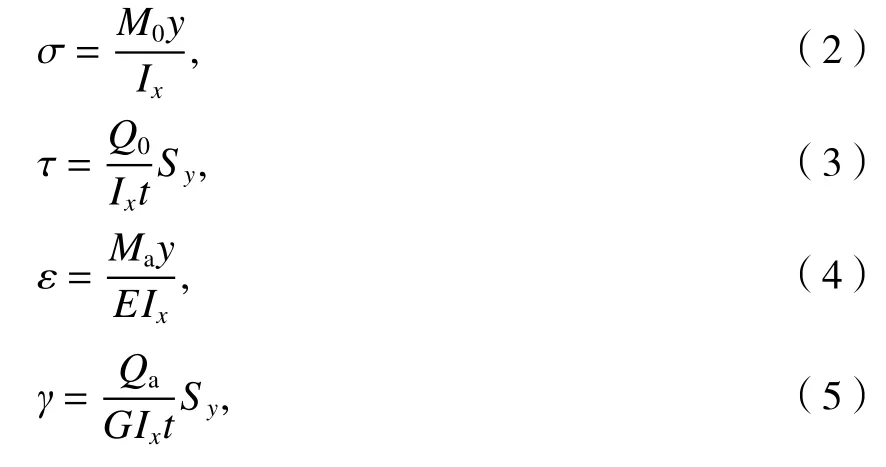
式（2）～（5）中：Ix为箱梁截面关于x轴的惯性矩；Sy为微元板的静距；Ma、Qa分别为实际荷载p(z)在微元截面产生的弯矩、剪力；E、G分别为箱梁材料的弹性和剪切模量.

由式（2）～（4）可知，挠曲应力σ和τ在微元板上做的内虚功dWin表示为

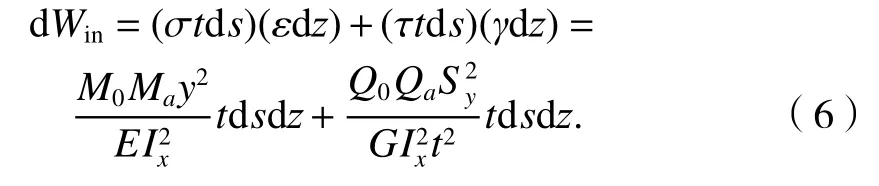
可求得箱梁的总内功为

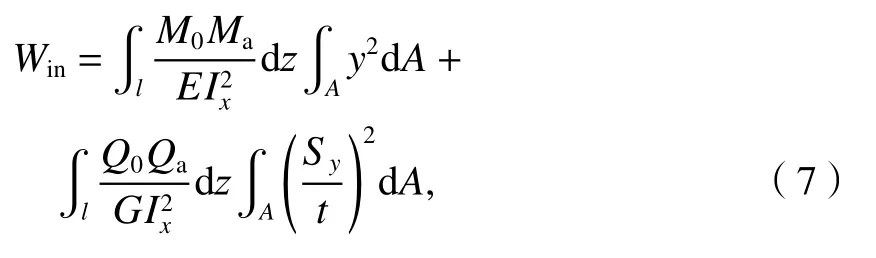
式中：A为箱梁截面面积；l为梁长.

为了形式统一且表示方便，引入截面剪切影响系数k如式（8）所示.

将式（8）代入式（7），并根据虚功原理Wex=Win，由式（7）与式（1）的关系，可求得

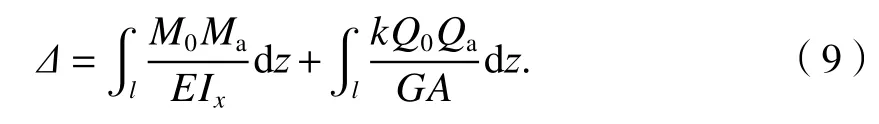
显然，式（9）等号右端第1项表示箱梁弯曲引起的挠度，第2项表示剪切引起的附加挠度.若能求解出适合于箱形截面的k，则通过式（9）很容易分析出图1所示的悬臂箱梁挠度.同样，若已知k时，对于考虑剪切变形影响的简单静定等截面箱梁结构挠度求解，可采用文献[14]的计算式，在此不再赘述.

2 箱梁剪切影响系数分析

由式（8）可知，欲求箱梁的剪切影响系数，需分析箱梁截面各个微元面积与箱壁厚的比值函数.对图1所示的箱梁截面，当其发生竖向挠曲时，根据薄壁箱梁的弯曲理论和截面的对称性[15]可知，箱梁任意点的弯曲剪力流（在箱梁顶板对称中心处虚设开口，且逆时针为正）如式（10）所示.

式中：Q(z) 为箱梁截面承受的剪力.

由式（10）可得箱梁任意点的弯曲剪应力为

观察式（11）与式（8）可知，箱梁微元的面积静矩与壁厚的比值与弯曲剪应力成正比关系.由此可给出箱梁任意断面的剪应力分布如图3所示，图中：α为斜腹板与竖轴的交角.

通过图3分析可得箱梁顶板处S y与t的比值ξd可表示为

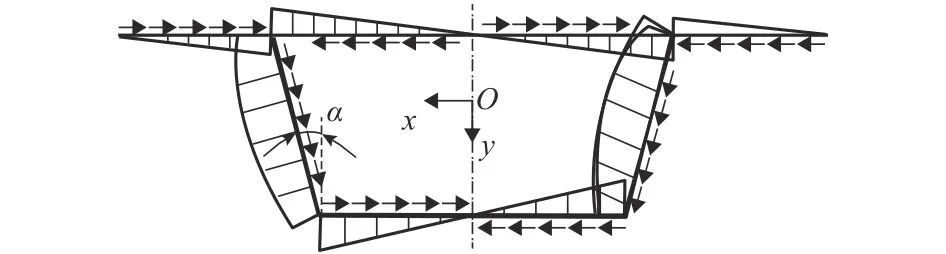
图3 箱梁弯曲剪应力分布示意Fig.3 Bending shear stress distribution of box girder

同样，对应箱梁悬臂板与底板处S y与t的比值分别为ξc和ξb，如式（13）、（14）所示.

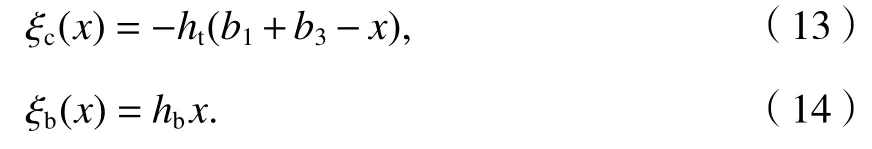
将式（12）～（14）代入式（8），化简后求得箱梁翼板剪切影响系数kf为

式中：At、Ac和Ab分别为箱梁顶板、两侧悬臂板和底板的面积.

分析剪应力分布可知，S y与t的比值沿箱梁腹板高度为二次函数.于是S y与t在腹板剪应力最大处（y=0）和任一点的比值分别为ξ0和ξw，表示为式（16）、（17）.

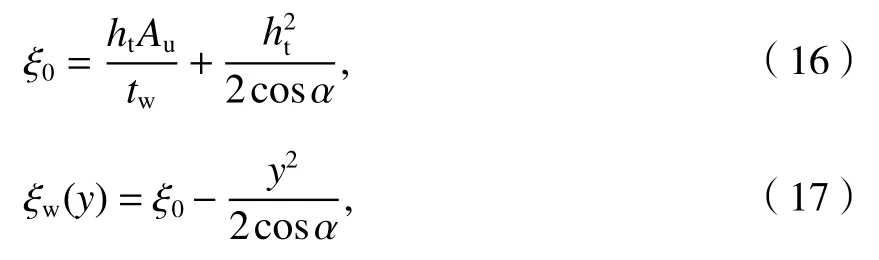
式中：Au为箱梁上半翼板的面积；tw为腹板厚度.

将式（17）代入式（8）后，可导出箱梁腹板的剪切影响系数kw为

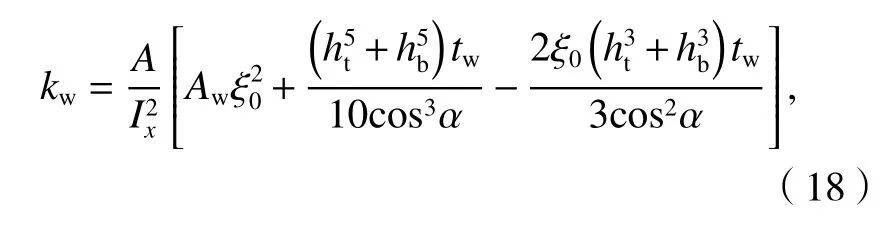
式中：Aw为箱梁腹板面积.

由式（15）和式（18）可求得

与文献[9-11]中求解薄壁箱梁挠度的方法不同，利用式（19）求得的剪切影响系数，再结合Timoshenko梁理论，可以在不分析箱梁剪力滞效应时求得较为精确的箱梁挠度，求解过程也相对简单.

3 梁段单元的刚度矩阵

利用剪切影响系数和文献[14]方法可方便求解等截面箱梁挠度，然而对于变截面复杂连续箱梁挠度的求解则需采用梁段数值方法.为此，取长度为L的有限梁段单元e如图4所示.图中：i、j为单元的两端节点；θi、θj分别为梁段的i、j端挠曲转角，与之对应的弯矩分别为Mi、Mj；wi、wj分别为梁段i、j端的竖向挠度，与之对应的剪力分别为Qi、Qj.

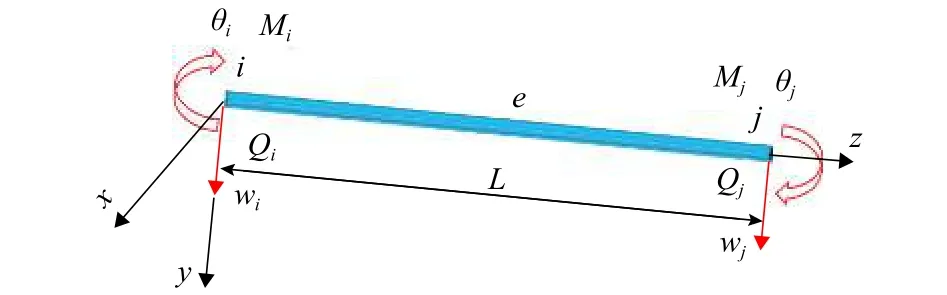
图4 有限梁段分析图示Fig.4 Beam segment analysis

对于悬臂箱梁，相当于梁段左端完全固定，即θi和wi均为0，于是梁段内任意点的剪力Q和弯矩M分别为

对于小变形的线弹性箱梁结构，其应变能为[16]

将式（20）～（21）代入式（22）可得

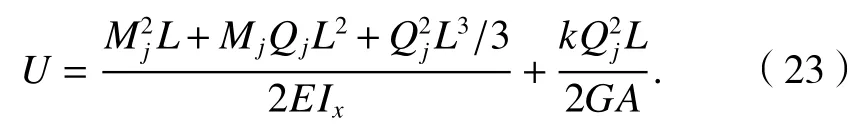
根据卡氏第二定律可知[16]

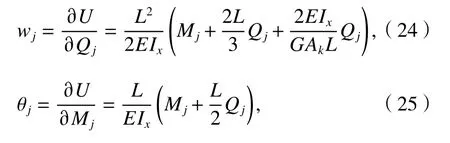
式中：Ak=A/k为箱梁的有效抗剪面积.

将式（24）和式（25）写成矩阵形式为

式中：φ=6EIx/(GAkL2).

对式（26）求逆矩阵可得

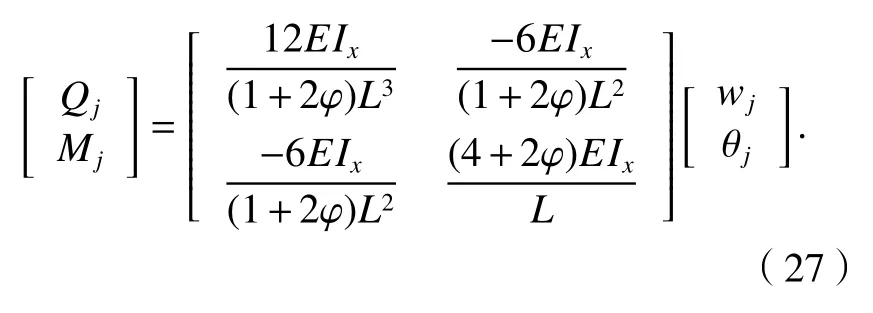
式（27）用矩阵符号表示为

式中：Fj为j端荷载列向量；Kjj为j端的近端刚度矩阵；δj为j端位移列向量.

根据节点力与节点位移的关系，建立图4梁段单元的节点力向量与节点位移向量的关系为

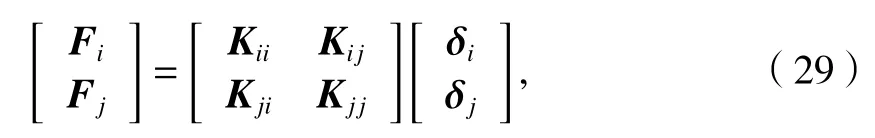
式中：Fi为i端荷载列向量；Kii为i端近端刚度矩阵；Kij与Kji分别为梁段单元e的i端和j端的远端刚度矩阵；δi为i端位移列向量.

当梁段δi=0 时，根据静力平衡条件可得

式中：H为平衡矩阵.

由于δj为任意值，将式（28）代入式（30）中，并根据式（29）与式（30）关系可得

当梁段δj=0 时，根据式（29）及式（32）可得

利用静力平衡条件式（30）及式（33）～（34），可得

将式（28）、式（31）～（35）代入式（29），求得考虑剪切影响的箱梁梁段单元刚度矩阵为

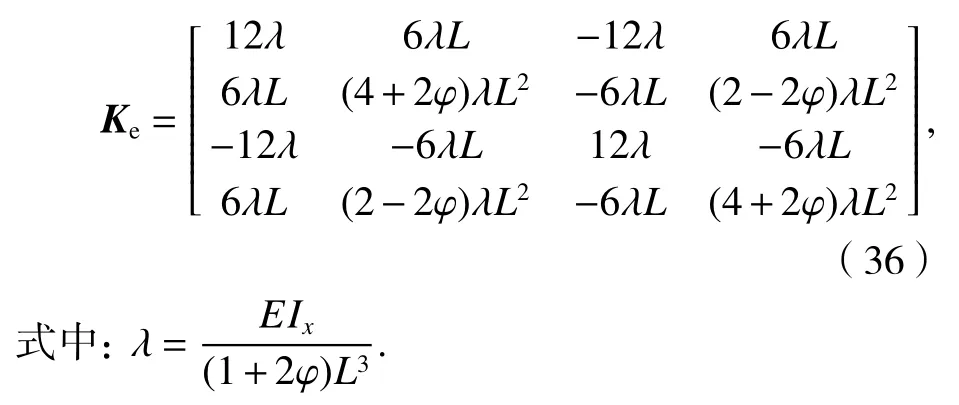
4 数值算例分析

4.1 等截面箱梁

模型箱梁截面如图5所示[5]，结构形式分别为单跨简支和两跨连续梁，跨长为80 cm，跨中承受集中荷载 1.6 kN.其材料特性为E=2.9 GPa，泊松比为0.4.

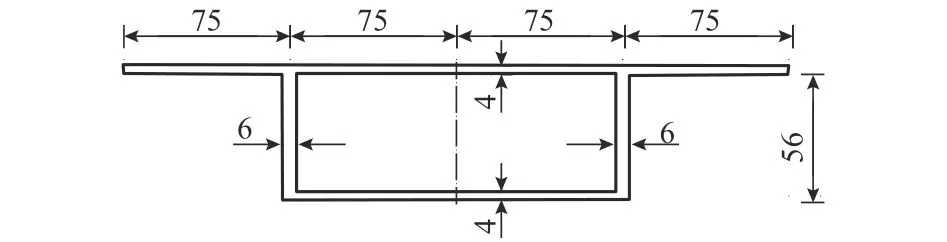
图5 模型梁截面Fig.5 Section of box girder model

为对比分析，分别按初等梁理论、本文方法、文献[5]方法和采用SHELL63壳单元建立ANSYS空间有限元计算上述箱梁的挠度曲线，如图6所示.

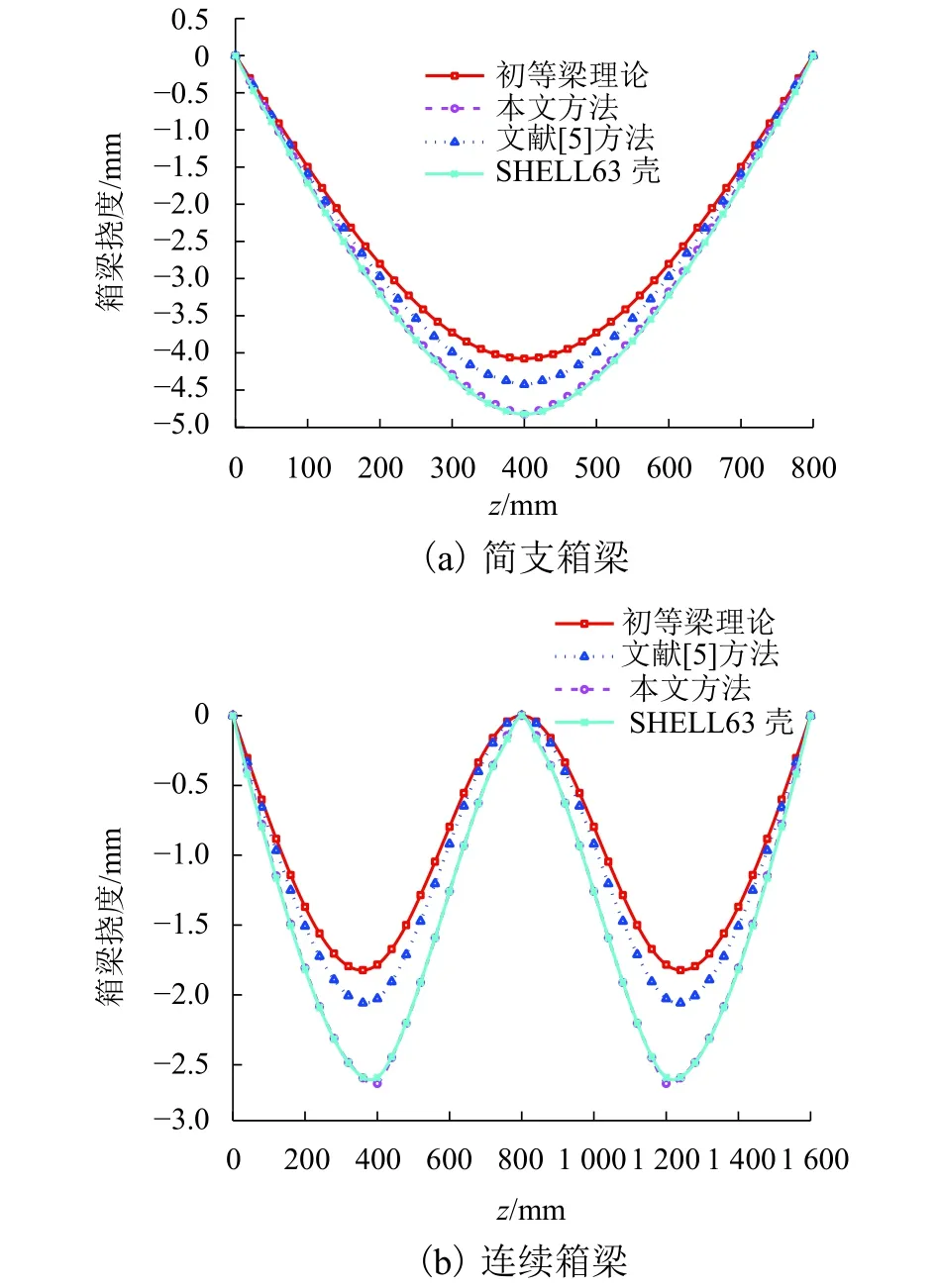
图6 等截面箱梁的挠度曲线Fig.6 Deflection curves of box girder with constant section

由图6可知，按照本文方法计算的箱梁挠度与SHELL63壳单元的空间有限元计算结果吻合良好，与初等梁理论和仅考虑剪力滞影响（文献[5]的方式）相比，挠度计算精度有较大提高.为了定量分析仅考虑剪力滞效应和考虑全截面剪切变形对等截面箱梁挠度的影响，表1分别给出了仅考虑剪力滞影响以及考虑腹板剪切影响（采用本文及文献[9]方式）时上述箱梁的计算挠度值.

由表1可知：考虑箱梁的全截面剪切影响时，计算箱梁挠度与实测值及空间有限元吻合较好；仅考虑剪力滞影响的箱梁挠度与空间有限元结果相差也达10%～20%，说明针对此箱梁，腹板的剪切对挠度影响较大.

表1 箱梁跨中挠度对比Tab.1 Comparison of mid-span deflection of box girders

4.2 变截面箱梁

以如图7所示的有机玻璃变截面连续箱梁[17]为例，变截面箱梁边跨端部和中跨跨中处各有6 cm长的等截面直线梁段.箱梁中支点梁高8 cm，边支点梁高4 cm，梁高按二次抛物线变化.有机玻璃的弹性模量为2.6 GPa，泊松比为0.4.施加于模型梁的荷载工况为：1）均布荷载施加于全梁，荷载值为5 N/cm；2）在中跨跨中截面施加集中荷载为137.33 N.

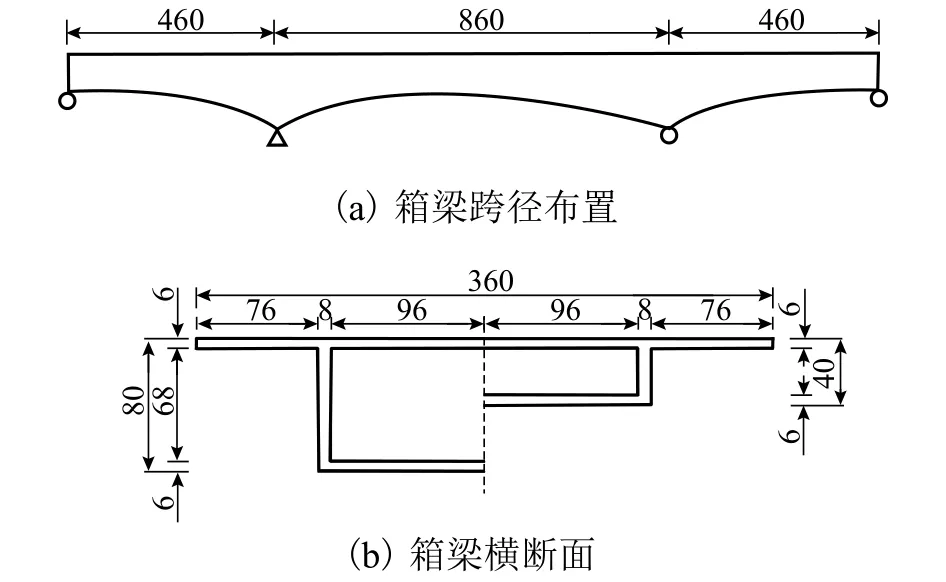
图7 变截面连续箱梁模型Fig.7 Continuous box girder model with variable section

基于前文的单元刚度矩阵，利用Fortran编制了箱梁梁段计算程序DBOX，分析上述变截面连续箱梁挠度.程序分析时，梁段单元长度选为10 mm，沿箱梁长度方向共划分为178个单元，单元的截面参数取为每个梁段的中心截面.为更加清楚了解箱梁的翼板和腹板剪切变形影响，分别以kf和k计算上述变截面箱梁模型挠度.为对比分析，分别采用文献[6]的分析方法和利用SHELL63壳单元建立的ANSYS空间有限元模型计算所得该箱梁挠度曲线，如图8所示.

由图8可知：仅考虑翼板剪力滞效应时，本文方法与文献[6]吻合良好；综合考虑截面剪切影响时，本文梁段程序计算的箱梁挠度与空间有限元结果吻合良好，说明本文方法求得的挠度精度较高；不同荷载作用下，剪切变形均使得中跨箱梁挠度有显著提高.为更准确分析翼板和腹板剪切变形对该变截面箱梁中跨挠度的影响，若以vf和vw分别表示翼板和腹板剪切变形引起的附加变形，vc表示初等梁理论的挠度，表2给出上述变形在箱梁跨中部位的挠度值.

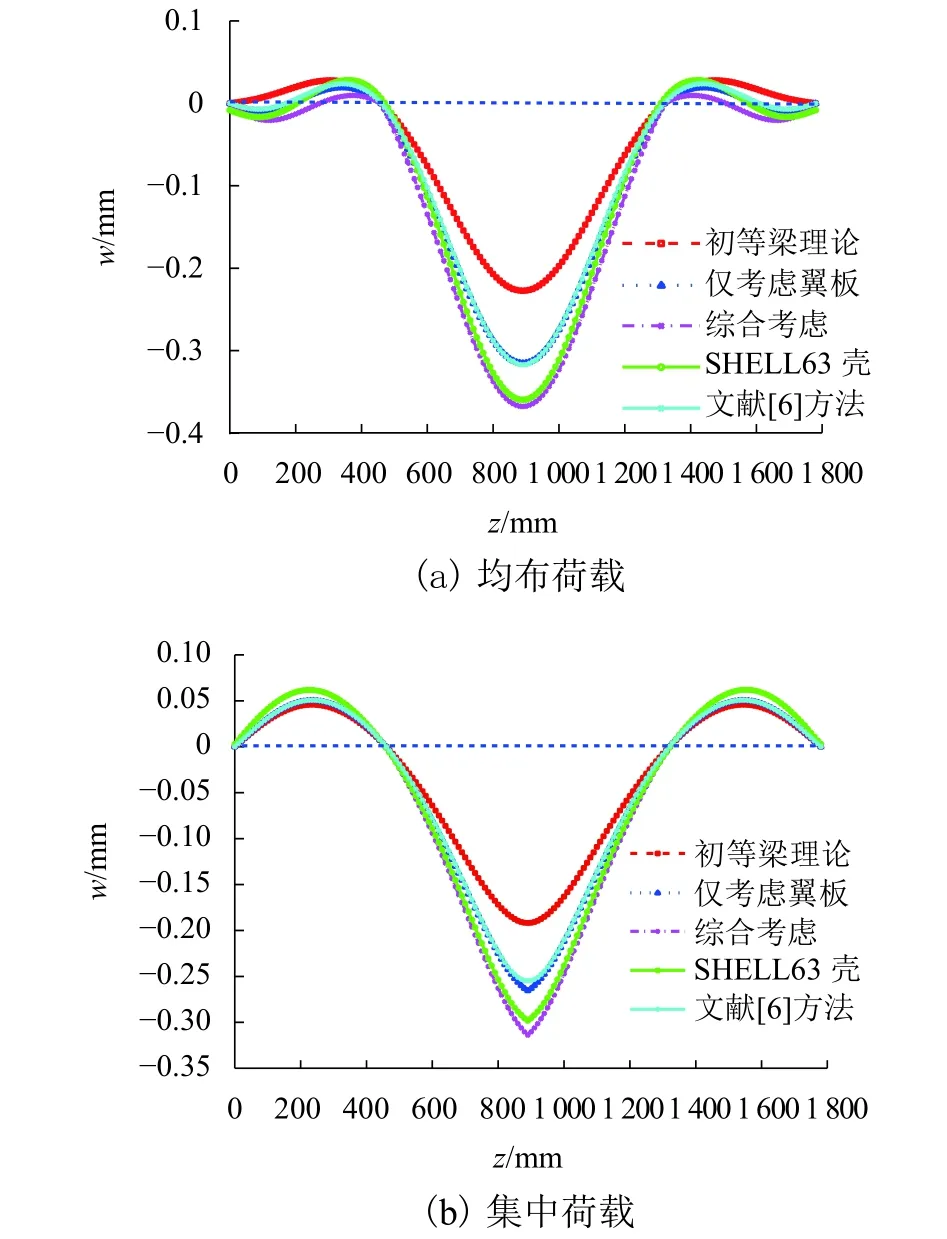
图8 荷载作用下箱梁挠度曲线Fig.8 Deflection curves of box girder under load

表2 跨中截面处挠度分析Tab.2 Mid-span deflection analysis

由表2可得，该变截面箱梁翼板和腹板剪切变形产生的挠度已达忽略剪切变形计算挠度的25%～38%.

4.3 参数分析

在文献[9-11]中，薄壁箱梁腹板的剪切影响系数ks为A/Aw.为分析该系数与本文给出的剪切影响系数之间的差异，图9以算例1所示截面为基础，给出了剪切影响系数与宽高比2b1/h的关系曲线.

由图9可得：宽高比对剪切影响系数影响较大，宽高比较小时两种腹板剪切影响系数值接近，但当宽高比较大时，采用文献[9]方式计算的腹板剪切影响系数值可能会过大，因此会过高估计腹板的剪切变形的影响.

图9 剪切影响系数Fig.9 Shear influence coefficient

为分析腹板和翼板剪切变形对箱梁挠度影响的大小，图10给出kf和kw与k的剪切影响系数占比随宽高比的变化.

图10 各板的剪切影响系数占比Fig.10 Proportion of shear influence coefficient of each board

由图10可得：随着宽高比的增大，翼板剪切影响系数占比会增大，而腹板占比减小，说明随着宽高比的增大，翼板产生剪切挠度会增大而腹板则与之相反.

5 结 论

1）通过单位荷载法，结合箱梁弯曲剪应力的分布特点，分析出适合于箱形梁的剪切影响系数.在该剪切影响系数的基础上，利用卡氏第二定律及梁段刚度矩阵特性，导出考虑截面剪切影响的箱梁梁段单元刚度矩阵，并编制了相应的箱梁挠度计算程序.

2）分别以等截面和变截面箱梁为数值算例，采用本文方法计算的挠度与空间有限元结果及实测值吻合良好.与已有文献方法相比，本文计算方法在不损失挠度计算精度时，可略去分析箱梁剪力滞效应的复杂过程，从而大大简化分析过程，提高计算效率，是一种十分简便的分析方法.

3）本文的变截面算例结果表明：翼板剪切变形致使挠度增加约38%，而腹板剪切变形使挠度增加约25%以上；参数分析表明，随着宽高比的增大，翼板剪切产生的附加挠度会增大，而腹板则与之相反.

致谢：甘肃农业大学公招博士科研启动基金（GAUKYQD-30）与水利水电学院创新基金（SLXY-QN-2020-05）的资助.