一种改进的病态测距方程非线性估计的正则化数值迭代法

张建霞，曲国庆，席 换，王 晖

(山东理工大学 建筑工程学院，山东 淄博 255000)

测距定位方程用来描述已知点和待测点之间的欧氏距离，是大地测量与导航定位中重要的观测方程[1]。该方程是非线性方程，传统方法利用非线性最小二乘法，依据泰勒级数展开至一阶项进行求解，适用于初值精度高和非线性强度弱的情况；对于非线性强度较强的模型，线性近似产生的模型误差可能大于观测误差，给观测方程带来系统性的误差，降低解的精度和可信度[2-3]。对于这类问题，可采用智能优化算法或将其线性化展开至二阶项进行求解[4-7]。对于残差小的非线性方程，一般采用高斯牛顿迭代法进行求解[8]。但是，若测距定位方程存在病态问题时，初始迭代矩阵具有严重的病态性，基于非线性最小二乘的数值迭代法会出现强烈的不稳定现象，无法收敛[9-10]。因此，根据测距定位方程的病态机制，选择合适的求解病态非线性方程的方法就显得尤为重要。

针对短程测距问题，有学者研究了测距定位方程非线性最小二乘解的性质，指出非线性最小二乘解是观测向量末端以观测权为质量的质点系的重心，发展了短程测距定位方程的重心迭代方法和封闭式牛顿方法，能够一定程度缓解短程测距的病态问题[11-13]。近年来的研究包括基于数值最优化理论通过附加稳定泛函或者避免迭代矩阵取逆运算，优化迭代步长来提高短程测距定位的收敛效率、稳定性和可靠性[1，14-15]。非线性正则化数值方法在处理病态测距定位问题的应用过程中过于硬套，多集中于数值方法的构建，但在大地测量中，测距定位方程的病态问题主要是因为已知点和未知点近似共面，如三维测边网、室内定位方程和水下测距定位方程，导致测距定位方程在高程方向即Z方向产生病态问题[16]。传统非线性正则化数值迭代法假设各个方向都存在病态问题，给各个方向附加正则化约束，这会严重加剧问题的复杂性、非线性收敛效率和解的可信度。

因此，针对大地测量观测构型缺陷产生的病态问题，提出一种改进的病态测距方程非线性估计的正则化数值迭代法。该方法采用分方向处理的思想，将非线性正则化约束只作用于病态方向，不对态性良好的水平方向进行约束，这样既保证水平方向能够稳定收敛到非线性最小二乘解，又能够有效降低病态方向对参数估计解的影响。本研究通过分析正则化参数与协方差的关系，提出采用协方差迹最小准则来确定正则化参数。最后采用病态仿真数据和实测数据，验证了该方法的有效性。

1 病态测距定位方程的非线性正则化数值迭代法

假设某观测系统中，共存在n个已知点，第i个已知点可表示为(xi,yi,zi)，已知点到未知点的观测距离为L1,L2,…,Ln，所对应的观测误差为ε1,ε2,…,εn。要求根据已知点坐标和观测距离来确定未知点的几何位置(x,y,z)，观测数据和已知点坐标n≥4，即可列出超定测距定位方程：

Li=di(x)+εi，

(1)

(2)

其中Δi为线性化残余误差。

大地测量与导航定位中，由于观测几何结构设计问题导致测距定位方程具有病态性，比如已知点与待测点近似共面会导致测距定位方程在Z方向产生病态问题，为将病态方向与态性良好的方向分开讨论，可将观测方程表示为：

(3)

忽略线性化余项，可构建线性化平差模型的向量表达式：

L=B1dr+B2dz+ε，

(4)

式中，dr=[dx,dy]T为水平方向坐标信息变化量；dz为高程方向坐标信息变化量；B1为平面方向的方向矢量，即水平方向所对应的设计矩阵；B2为Z方向的方向矢量，即Z方向所对应的设计矩阵。根据式(4)可得线性化误差方程：

V(x0)=B1dr+B2dz-l，

(5)

式中，l=L-d(x0)。上述方程的最小二乘解使残差在平方意义上取极小值min：

(6)

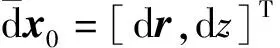
(7)

将式(5)代入式(7)进行化简，考虑到线性化初值精度，可构建高斯牛顿迭代公式：

(8)

其中k为迭代次数。

高斯牛顿法收敛条件相对于牛顿法更加严格。对于一般非线性最小二乘问题，文献[17]利用几何性质证明高斯牛顿法的适应条件取决于残差的大小和非线性强度。当残差较大或者设计矩阵存在病态时，此时高斯牛顿法易陷入死循环或者得到的解并非有效解[15]。为解决测距定位方程的病态问题，传统方法是基于标准稳定泛函约束的正则化方法，其目标函数为：

(9)

其中α为正则化参数，主要用来平衡解的不稳定性和平滑性[10]。考虑到线性化初值，将目标函数对待估参数求一阶偏导数令其等于零，结合式(5)进行化简可得：

(10)

式(10)为传统非线性正则化迭代法。

由式(10)可知，传统非线性正则化迭代法假设各个方向具有相同的病态问题，因此将稳定泛函作用于所有方向，这种假设能够提高解的稳定性，但并不切合实际，增加了问题的复杂度且降低了数值算法的收敛性。大地测量与导航定位中，观测结构共面导致的病态问题较常见，先计算设计矩阵的条件数证明存在病态，再利用特征分析法求得3个方向对应的特征值，一般将“特征值很接近于零”作为判断方程病态性的依据[18-19]来判断病态方向。针对共面导致的病态集中于Z方向的问题，给出一种改进的正则化数值迭代法，即

(11)

该方法采用分方向处理病态问题的思想，降低了问题的复杂度，能保证水平方向上仍然为最小二乘解，在降低病态性对解的影响的同时提高收敛效率。

2 正则化参数的确定

精确确定正则化参数是保证病态测距定位方程的非线性正则化迭代法解算效果的关键，过大或过小都会影响参数估计解，过大会导致解算模型过度平滑，过小对问题解算未起到明显改善效果，解的不稳定性依然存在。本研究提出一种基于最小协方差迹来确定正则化参数的方法。设

(12)

根据协因数传播定律，结合式(12)可计算观测方程的协因数阵为：

(13)

根据分块矩阵求逆运算，可得到参数估计解垂直方向和水平方向的协因数阵

(14)

若不附加正则化约束，水平方向和垂直方向的协因数阵为：

(15)

由式(15)可知，测距定位方程Z方向的病态性也会影响水平方向即X和Y方向的求解精度，使X和Y方向也产生病态性的“虚假”问题。如果将正则化约束直接作用于所有的方向，虽能够改善问题的病态性，但加剧了问题的复杂性，降低了非线性迭代收敛效率。将式(15)减去式(14)可得：

(16)

由式(16)可知，在一定取值范围内，参数估计解的协因数阵与正则化参数呈递降关系。通过将正则化参数作用于Z方向能够降低Z方向病态给水平方向即X和Y方向产生的影响。取水平方向和垂直方向的互协因数阵为Qdrdz，则可计算参数估计解的协方差估计值

(17)

(18)

综上分析，参数估计解在水平方向和垂直方向的方差是α的递降函数，这表明在适当条件下，方差会随正则化参数的增加而降低，但由于系统残差以及偏差等问题，方差会逐渐趋于稳定值。由于协方差迹能够整体反映该方法的求解精度，可设计如式(19)最优化函数来计算正则化参数：

(19)

式(19)为协方差迹最小准则函数，类似于采用L曲线法来确定正则化参数，其搜索结果如图1所示，协方差随着正则化参数的增加而降低，最后趋于稳定，形状类似于L形。

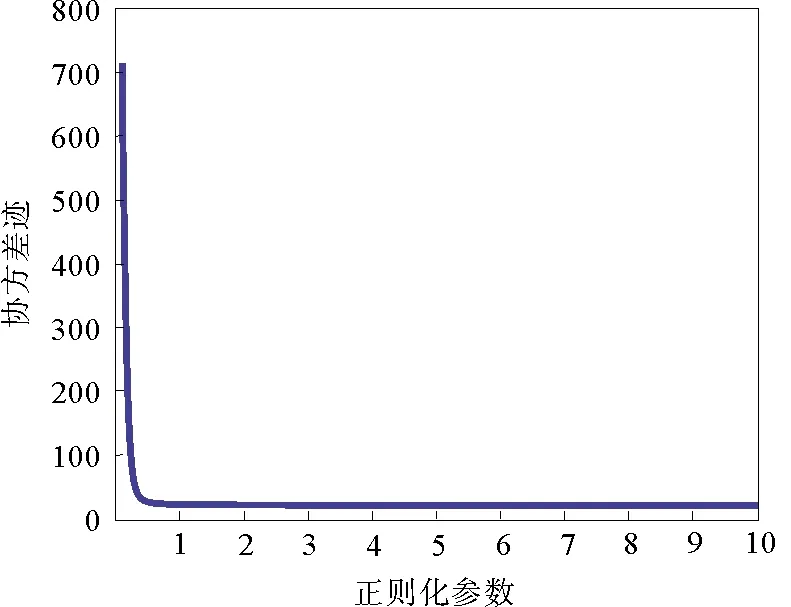
图1 基于协方差迹最小准则确定正则化参数搜索结果

3 算例

3.1 算例1：短程测距定位模拟实验

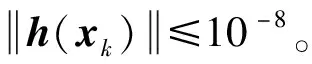
由表1数据构造的短程测距定位方程是非线性方程，且已知点和待定点呈近似共面分布，计算设计矩阵的条件数为115.052 0，存在中等程度的病态，再计算设计矩阵3个方向上的特征值分别为6.719 4、1.222 2、0.058 4，Z方向上的特征值最接近于0，可判断该方程的病态性主要集中于Z方向，X方向和Y方向态性良好。对于这类病态问题，分别采用非线性最小二乘法、高斯牛顿法、传统非线性正则化迭代法和本研究方法进行计算并对比收敛结果和迭代次数，结果如表2所示。

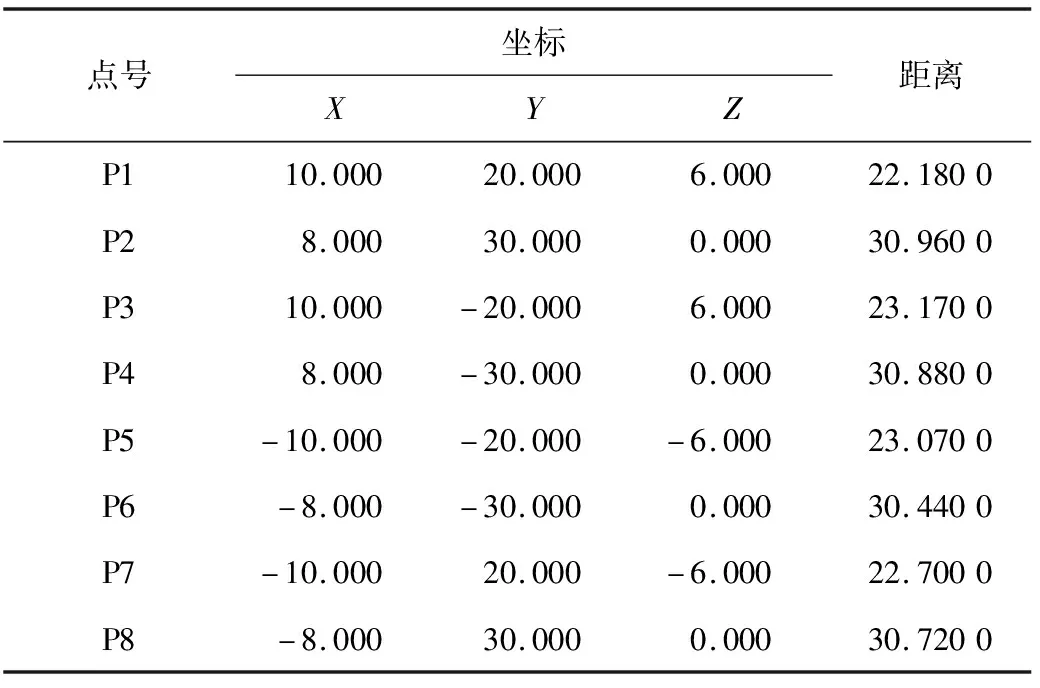
表1 短程测距定位已知点的三维坐标和已知观测距离

由表2给出的4种方法的数值收敛解对比可知，非线性最小二乘法虽然简单易实现，但由于受到病态的影响，解的精度较差，结果不可靠，尤其是Z方向上的解与真值的偏差最大，进一步证明了该方程的病态性集中于Z方向；高斯牛顿法在处理病态问题时，受到强烈扰动而使解不稳定，无法收敛到数值解，因此不适用于病态方程组的解算；传统非线性正则化迭代法和本研究方法基于稳定泛函约束的思想，降低了病态问题对方程组解的影响，提高了非线性最小二乘解的精度；而本研究方法既保证水平方向能够稳定收敛到传统意义上的非线性最小二乘解，又能够有效降低病态方向对解的影响，通过迭代次数比较，说明本研究方法能够较快地得到数值收敛解，提高了传统非线性正则化迭代法的收敛效率，在处理大地测量中已知点和待定点近似共面导致的病态问题时具有良好的性能。

表2 不同方法的解算结果(算例1)

图2给出了本研究方法和传统非线性正则化迭代法的点位迭代序列，横轴代表迭代次数，纵轴分别代表X、Y、Z3个方向上的数值收敛解。由图2可知，该方法没有影响解的稳定性，且能更快地收敛到估计解，具有良好的性能。对于水下GPS定位、室内导航定位等短距离测距定位方程，也存在已知点和未知点近似共面的情况，本研究方法仍然适用。

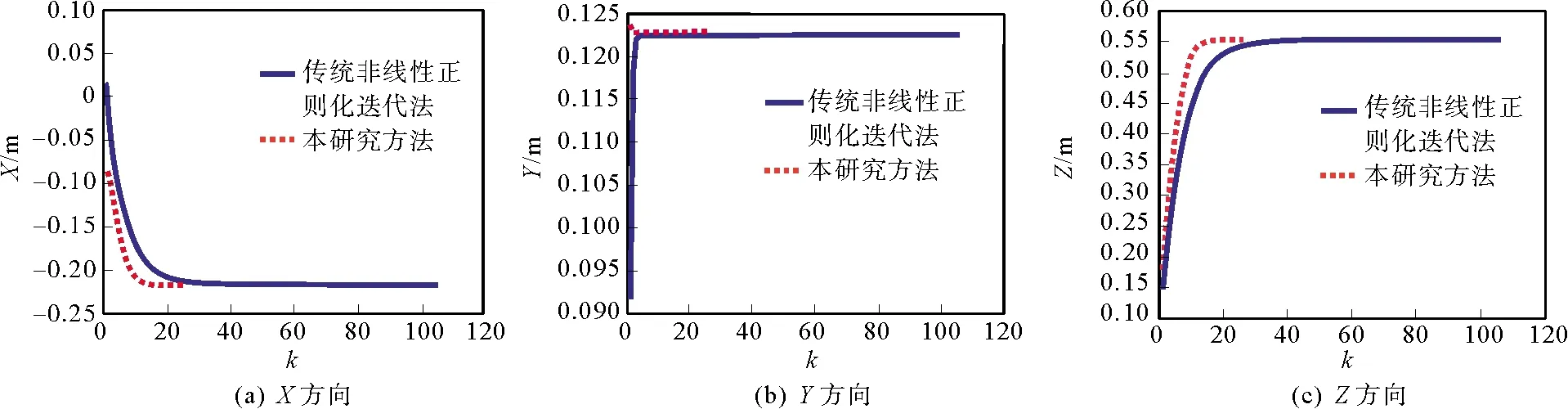
图2 2种方法的点位迭代序列图(算例1)

3.2 算例2：蜂窝网定位模拟实验

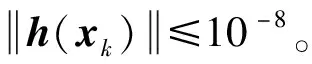
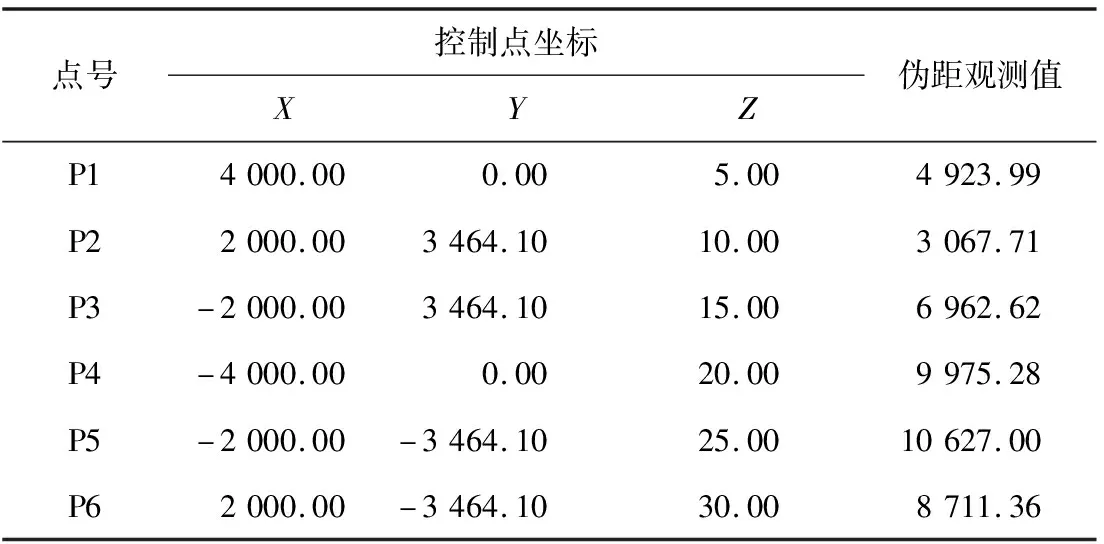
表3 蜂窝网已知点的三维坐标和已知观测距离

在蜂窝网的三维定位中，控制点和未知点一般都近似分布于地表，即控制点和未知点近似共面，测距定位方程的设计矩阵存在病态问题。计算设计矩阵的条件数为1.563 0×106，方程存在严重病态，再计算设计矩阵3个方向上的特征值分别为10.449 5、1.518 7、0.031 8，Z方向上的特征值最接近于0，可判断该方程的病态性主要集中于Z方向，X和Y方向的病态性较弱。同算例1，分别采用4种方法进行计算，结果如表4所示。

表4 不同方法的解算结果(算例2)

由表4可知，从数值收敛解来看，非线性最小二乘法得到的收敛解误差较大，尤其是Z方向的解偏离真实值最大，解算结果不可信，证明Z方向确实受病态影响最大，病态主要集中在Z方向；高斯牛顿法不适用于处理病态方程，易受到初值的约束和病态的影响，使解无法收敛；传统非线性正则化迭代法和本研究方法虽然得到收敛解的数值相同，但该方法在水平方向得到的还是传统意义上的非线性最小二乘解，但因为Z方向受到正则化约束的作用，使得Z方向上解的病态性减弱，误差减小，同时因为方程整体病态的减弱也影响了其余2个方向的解，与模拟真值更相近，提高了非线性最小二乘法的精度。从迭代次数对比来看，该方法提高了传统非线性正则化迭代法的收敛效率，具有良好的性能。

图3给出了传统非线性正则化迭代法和本研究方法的点位迭代序列图，从图中可以看出，该方法在提高收敛效率的同时稳定性并没下降，能更早更快的趋于收敛。结合表4可以得出结论：该方法在处理病态测距定位方程时表现出良好的性能。

图3 2种方法的点位迭代序列图(算例2)

3.3 算例3：水下定位实测数据实验

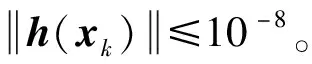
表5 不同方法的解算结果(算例3)

由表5可知，非线性最小二乘法得到的收敛解误差较大，解算结果不可信，尤其是Z方向上的解与真值的偏差最大，证明Z方向上的病态性最强；高斯牛顿法这类普通的数值迭代法易受到初值的约束和方程病态性的影响，解无法收敛，不适用于处理病态问题。与传统非线性正则化迭代法相比，本研究方法性能更优。因此，对于水下定位存在的已知点和未知点近似共面的情况，该方法也能表现出良好的性能，适用于实际问题。

图4给出了传统非线性正则化迭代法和本研究方法的点位迭代序列。从图中可以明显地看出，该研究方法开始收敛的早，稳定性较好，没有较大的扰动，并且大大提高了传统非线性正则化迭代法的收敛效率，表明本方法在水下定位的实际应用中能够发挥良好的性能。

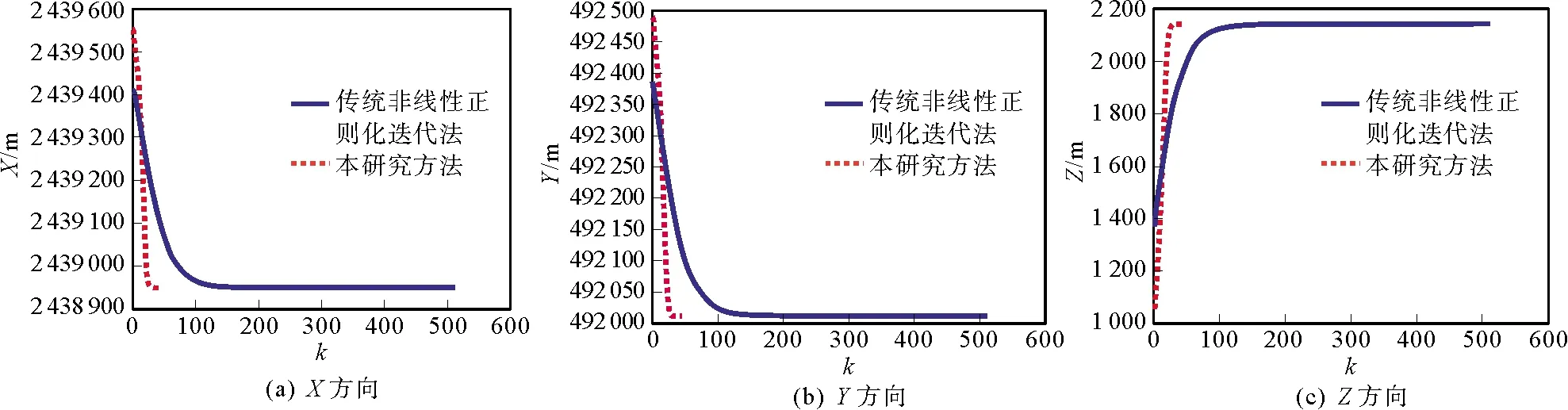
图4 2种方法的点位迭代序列图(算例3)

4 结束语

在大地测量中，非线性正则化数值迭代法被广泛地应用于病态测距定位方程的解算中。然而，在测距定位中，常出现已知点和未知点近似共面的情况，此时方程线性化后的设计矩阵具有病态性，通过条件数法和特征分析法可以判断病态主要集中于Z方向。本研究提出一种改进的非线性正则化数值迭代法，将正则化约束仅作用于病态方向，来提高非线性收敛效率，增强解的稳定性。实验结果表明，本研究方法能够降低病态性对解的影响，提高传统非线性正则化迭代法的收敛效率，具有更好的局部收敛性质。