一类四阶弹性梁方程正解的存在唯一性
2021-07-02韦孝东白占兵
韦孝东,白占兵
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
研究如下四阶两点边值问题正解的存在唯一性:
z(4)(t)=f(t,z(t),z′(t),z′′(t)),0 (1) z(0)=z′(1)=z′′(0)=z′′′(1)=0, (2) 这里f:[0,1]×R3→R是连续的。 梁是工程建筑的基本构件之一,材料力学和工程物理中常用四阶常微分方程边值问题来描述弹性梁的状态。基于这类问题的普遍性与重要性,四阶两点边值问题受到了广泛的关注,也取得了许多重要研究成果,见文献[1-14]。 1986年,Aftabizadeh[1]首次讨论了如下边值问题: z(4)(t)=f(t,z(t),z′′(t)),0 (3) z(0)=z(1)=z′′(0)=z′′(1)=0。 (4) 在边值条件(2)下的其他四阶边值问题也被广泛研究。2009年,姚庆六[7]研究了问题(2)~(5)正解的存在性与多解性: z(4)(t)=f(t,z(t),z′(t)),0 (5) 通过构造适当的积分方程并利用锥上的不动点定理证明了问题(5)~(2)在满足与n有关的条件下存在n个正解(其中n是自然数)。2012年,文献[8]利用度数理论中的Krasnosel'skii不动点定理、实变函数中的Lebesgue控制收敛定理和Fatou引理证明了两个新的正解存在定理。2011年,路慧芹[9]通过构造一个特殊的锥,利用锥上的不动点定理研究了问题(2)~(5),得到了方程存在正解的一个充分条件。 由Gupta[10]的经典分析可知,问题(1)~(2)是六种典型的弹性梁方程之一,描述了一类一端简支,另一端滑动夹紧的弹性梁的形变。2013年,郭环[11]研究了问题(1)~(2)解的存在性问题,由Schauder不动点定理和上下解方法得到了正解存在的充要条件。虽然可以通过上下解方法得到问题(1)~(2)的解,但在实际应用中上下解选取的难度比较大。 受以上工作的启发,研究问题(1)~(2)正解的存在唯一性。通过给出问题的Green函数并研究其相关性质,使算子A的定义更加明确。得到的Green函数在文献[7-9]中都有所提及,与上述文献不同的是,通过Laplace变换求Green函数更加直观易懂。在Banach空间中构造了一个闭球B[O,L],由Schauder不动点定理证明了问题解的存在性,由压缩映射原理证明了问题解的唯一性,解的正性也被讨论。最后给出了一个数值例子。 引理1.1给定k(t)∈C[0,1], (6) 是如下边值问题的唯一解: z(4)(t)=k(t),0 (7) z(0)=z′(1)=z′′(0)=z′′′(1)=0。 (8) 这里,G(t,s)是该问题的Green函数: (9) 证明:对式(7)进行拉普拉斯变换得: s4Z(s)-s3z(0)-s2z′(0)-sz′′(0)-z′′′(0)=K(s), 这里,Z(s)=L[z(t)],K(s)=L[k(t)]。易知: 由边值条件z(0)=z′′(0)=0,得 因此: (10) (11) (12) (13) 将t=1代入式(11)和式(13),由边值条件z′(1)=z′′′(1)=0,得 代入式(10),得 证毕。 引理1.2由(9)式定义的Green函数有如下性质: 1)G(t,s)≥0,G1(t,s)≥0,G2(t,s)≥0,对∀t,s∈[0,1]。 证明:由式(9),有 (14) (15) 由式(9)、(14)和(15)可知,G(t,s)≥0,G1(t,s)≥0,G2(t,s)≥0。 再由 同理, 即 证毕。 引理1.3给定k(t)∈C[0,1],令 证明:由引理1.2易知结论成立。 引理1.4[12]设A1,A2,…,Ai是C[0,1]→C[0,1]的全连续算子,函数f(t,x1,x2,…,xi)在[0,1]×Ri上是连续的,则非线性算子A: (Ak)(t)=f(t,(A1k)(t),(A2k)(t),…,(Aik)(t)) 是C[0,1]上的全连续算子。 定义一个集合 (16) 这里L>0是一个实数。在C[0,1]中定义一个球心在O半径为L的闭球B[O,L]。定义一个非线性算子A:C[0,1]→C[0,1], (Ak)(t)=f(t,(A1k)(t),(A2k)(t),(A3k)(t)), 定理2.1假设存在一个正数L>0使得 |f(t,z,r,p)|≤L,(t,z,r,p)∈DL。 (17) 这里f:[0,1]×R3→R是连续的。那么,问题(1)~(2)至少有一个解。 同时,由式(17)可知 |(Ak)(t)|=|f(t,z(t),r(t),p(t))|≤L, 所以,(Ak)(t)∈B[O,L],即算子A是B[O,L]→B[O,L]的映射。 由Schauder不动点定理可知,算子A至少有一个不动点,即问题(1)~(2)至少有一个解。 证毕。 定理2.2假设定理2.1的(17)式成立,且存在三个常数M1,M2,M3≥0使得对∀(t,zi,ri,pi)∈DL,i=1,2,有 |f(t,z2,r2,p2)-f(t,z1,r1,p1)|≤M1|z2-z1|+M2|r2-r1|+M3|p2-p1|, (18) (19) 则问题(1)~(2)有唯一解z(t)∈B[O,L]⊂C[0,1],且满足 证明:只需要证明算子A是一个压缩映射即可。事实上,因为B[O,L]⊂C[0,1],所以B[O,L]是完备距离空间。由式(18)及引理1.3,对k1(t),k2(t)∈B[O,L],有 ‖(Ak2)(t)-(Ak1)(t)‖ =‖f(t,z2(t),r2(t),p2(t))-f(t,z1(t),r1(t),p1(t))‖ ≤M1|z2(t)-z1(t)|+M2|r2(t)-r1(t)|+M3|p2(t)-p1(t)| =q‖k2(t)-k1(t)‖。 即 ‖(Ak2)(t)-(Ak1)(t)‖≤q‖k2(t)-k1(t)‖。 结合式(19),算子A是一个B[O,L]→B[O,L]的压缩映射,因此算子A在B[O,L]中有唯一不动点,即问题(1)~(2)有唯一解z(t)。 下面考虑一种特殊的情况,定义两个特殊的集合: (20) SL={k(t)∈C[0,1]|0≤k(t)≤L}。 (21) 0≤f(t,z,r,p)≤L, (22) 且满足式(18)~(19),则问题(1)~(2)有唯一非负解。 推论2.1如果存在0 迭代方法如下: 1)给定一个初始方程k0(t)=f(t,0,0,0),t∈[0,1]; 迭代解zj(t)和精确解z*(t)满足如下估计: 例1考虑如下四阶边值问题: (23) z(0)=z′(1)=z′′(0)=z′′′(1)=0。 (24) ≤L, 解不等式得1.228 另一方面,对(t,z,r,p)∈DL, 取M1=1.5,M2=0.6,M3=0.5,则定理2.2的式(18)成立。 定理2.2的式(19)成立。 所以,问题(23)~(24)有唯一解(迭代过程见图1)。
1 预备知识和引理
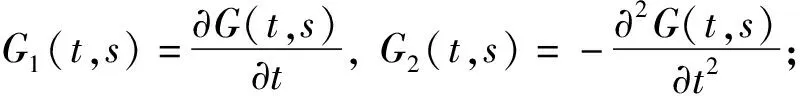


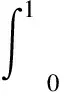
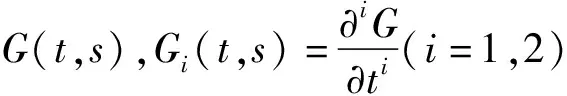
2 存在唯一性
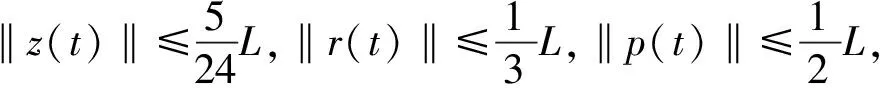

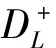
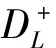
3 迭代方法和数值例子