基于三维扫描模型的兵马俑足踝有限元分析

兰德省，易伟同，祝 磊，蒋永慧，胡云岗，侯妙乐

(1. 秦始皇帝陵博物院，陕西西安 710600； 2. 北京建筑大学土木与交通工程学院，北京 100044；3. 北京建筑大学测绘与城市空间信息学院，北京 100044)

0 引 言

中国作为历史悠久的文化大国，留下了许多宝贵的文物，具有重要的历史研究价值[1]。其中陶质文物具有鲜明的中华民族特征，反映了近万年的文化演变、技术发展和社会变迁，是中华民族先民们所遗留下来的最宝贵的历史文化遗产之一[2]，兵马俑则是中国古代陶质文物的杰出代表[3]。兵马俑的修复与保护一直是文物保护领域的研究热点。

对于文物的保护和修复过程，常需要多学科、多领域的交叉融合共同完成。其与化学、物理学、地质学、生物学、历史学、文物保护学、考古学、材料学、美学、力学等方面均有密切的联系。力学作为基础应用学科，在文物保护修复中有着十分重要的地位，在文物粘接修复、加固包装等方面均有诸多的应用[4]。作为大型陶质文物，兵马俑具有质地偏脆的特性，且体积和重量较大、形状复杂，因而无论在展陈、运输还是存储的过程中，都会受到各种荷载的影响。因此，通过对整俑结构进行力学分析，可了解俑体在外荷载作用下的应力和变形特性，确定整俑结构受力薄弱部位，从而提出有针对性的加固和修复措施，对确保俑体结构的安全稳定具有重要意义。

有限元法是一种计算机数值仿真力学分析方法[5]，具有化繁为简的特性，是一种适用性强、应用广泛、结果可靠的结构力学分析方法。在文物保护领域，有限元法较多用于大型古建筑结构，如塔式结构、古代桥梁、古代楼阁、大型石窟等，大多采用木或砖石材料建造而成，力学分析的内容多为地震工况[6-12]。对于陶质文物，其力学方面的研究多集中于材料力学性能方面[4，13]，对文物整体结构的力学特性研究相对很少。因而采用有限元法对兵马俑进行整体力学分析，对于陶质文物保护方面具有开创性的意义。

对于有限元分析而言，模型精度对分析结果的准确性具有重要影响。兵马俑形状不规则、拓扑关系复杂，因而采用传统建模软件和方法往往费时且精确度极差。而随着三维激光扫描、计算机可视化、图形图像处理、实物数字化、虚拟现实等技术的迅速发展，文物保护与修复工作也进入了信息化时代[14-15]。基于三维激光扫描、计算机可视化和图形图像处理技术的文物碎片逆向建模，则能形成精确的几何信息，为文物整体结构的力学分析提供可靠的实现基础。

然而，随着三维激光扫描技术的快速发展，三维点云采集工具更加精密，从而使得点云数据采集密度越来越高，数据量愈加庞大。海量的数据往往存在数据冗余，因而采用原始数据处理势必耗费巨大的时间成本，造成计算资源的浪费。因而，对海量点云数据进行简化处理显得尤为必要[16-17]。

本研究将利用三维扫描技术获取兵马俑残片的三维点云数据，逆向建立高精度的残片三维实体模型，并对足踝部分进行有限元力学分析，以研究重力作用下足踝部分的应力和变形特征，进一步探究点云简化对计算结果的影响，从而在保证计算精度情况下缩短建模时间。

1 材料与方法

1.1 材料、硬件设备与软件

材料：以一套较为完整的秦俑残片组为原型进行逆向建模。残片组包含46块残片，整俑高度约1.9 m，总重量约135 kg。其中足踝部分包含8块残片，总重量约35 kg。硬件设备：美国法如(FARO)公司的手持式三维激光扫描仪，该仪器可直接将点云扫描数据实时传输到逆向建模软件杰魔(Geomagic Studio)中。软件：点云逆向建模软件杰魔(雨滴科技公司，美国)，有限元前处理CAE软件Hypermesh(阿泰尔公司，美国)，有限元分析软件ABAQUS(达索公司，法国)。

1.2 点云模型的逆向重建

点云模型的逆向重建原理是将点连成线，进而生成面，最终形成实体。采用杰魔软件进行点云逆向重建，主要过程分为3个阶段：点云封装、网格修复和精确曲面。

选取足踝部分8块残片相应的点云，在点云降噪处理后进行封装，封装时最大三角形数设置为点个数的1.5倍。将封装后的三角网格模型通过网格医生功能进行错误修复，再利用填充孔功能将网格缺损处补齐。最后将修复后的三角网格模型通过精确曲面流程转化为NURBS曲面，从而实现点云模型的实体化。精确曲面流程包括构造曲面片、构造格栅和拟合曲面。对于构造曲面片的步骤，需要保证曲面的边界线路径不相交，同时尽可能减少曲面片角度过小的情况。模型各步骤的处理效果如图1所示。

图1 点云模型逆向重建过程

1.3 有限元模型的建立

1.3.1Hypermesh网格划分 Hypermesh是一个功能强大的有限元前处理软件，支持多种有限元计算平台的数据格式交换，在网格划分方面支持丰富的单元类型和灵活的划分方法。通过杰魔软件将NURBS模型导出IGS格式，再导入到Hypermesh中，可进行有限元网格划分。模型导入后的效果如图2a所示，可以看出Hypermesh将不同残片通过颜色进行区别。残片按照先左后右的顺序从1～8进行编码，其中1～3为右腿底部，4～6为左腿底部，7为右腿，8为左腿。

选取合理的网格类型是保证有限元计算结果收敛的必要条件。秦俑残片具有复杂的几何特征和拓扑关系，采用六面体单元时易出现因曲面过于复杂而造成的网格退化情况，从而影响计算精度[5]。因此，采用四面体实体类型(C3D4)作为网格划分单元。根据该陶俑足踝部分残片尺寸和形状，设置网格种子尺寸为4，最终划分的网格总数为82 254。网格划分后的效果如图2b所示。

图2 有限元建模

1.3.2网格导入与材料属性 在Hypermesh中将划分好网格的模型导出为INP格式，再以部件形式导入到ABAQUS中，并进行装配。装配后的足踝模型如图2c所示。可以看出，模型以四面体网格形式直接导入，因而无需再利用ABAQUS网格划分模块进行操作。

将导入的所有残片赋予陶体材料属性。对于有限元模型的单位体系，长度单位采用mm，力单位采用N，质量单位采用kg。因此对应的密度单位为kg/mm3，应力、强度单位为MPa(N/mm2)。参考现有对秦朝陶俑的力学性能研究[4]，陶体材料属性参数如表1所示。

表1 材料参数取值

1.3.3接触和约束 为简化计算，将相邻残片之间的接触网格面设置绑定约束，如图2d所示。除此之外，将整体模型的底部网格面的六个自由度全部约束，相当于模型固定在地面上，如图2e所示。

1.3.4荷载本研究模拟 整俑在重力作用下足踝部分的受力特性，因而将荷载分为两部分进行施加，如图2f所示。对于足踝部分，直接添加全局重力，设置重力加速度为9.8m/s2。对于上部结构，则通过施加表面外力的方式代替重力，施加面位于腿部残片上表面。

对应受力为上部结构重力的一半，即500 N。因此左腿施加的表面力为：

500/9 896=0.050 5(N/mm2)

对于右腿，其荷载施加表面形状近似于长轴为135 mm，短轴为80 mm的椭圆，因而表面积为：

π/4×140×90=9 896(mm2)

对于左腿而言，其荷载施加表面形状近似于长轴为140 mm，短轴为90 mm的椭圆，因而表面积为：

π/4×135×80=8 482(mm2)

对应受力同样为500 N。因此左腿施加的表面力为：

500/8 482=0.058 9(N/mm2)

2 结果与讨论

2.1 有限元分析结果

有限元分析结果中的应力应变图可直观反映秦俑残片的应力和变形规律。对于足踝部分而言，各残片的Mises应力如表2所示，整体应力云图如图3a所示。可以看出，模型最大应力位于左腿足踝处，为0.723 MPa，显著大于其他部位，说明左腿足踝处出现应力集中。对于右腿足踝处，其最大应力相对较小，为0.353 MPa。根据现有研究，秦俑陶片强度在3.6～18.5 MPa之间[4]，因此足踝部分的各处应力远小于材料强度，结构在重力作用下处于安全状态。

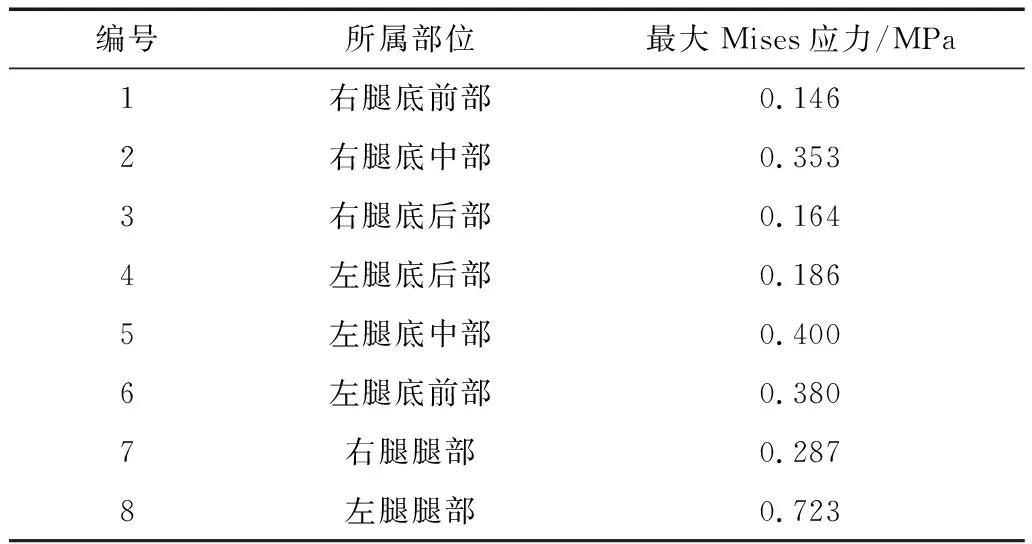
表2 残片Mises应力

图3 整体应力和变形结果

对于结构变形，整体形状如图3b所示(为清楚显示变形状态，将变形放大1 000倍进行展示)。可以看出最大变形同样出现在左腿，其对应的绝对值为0.080 mm。相比于右腿以竖向为主的变形特点，左腿变形还出现明显的侧向变形。

2.2 点云简化参数优化分析

2.2.1点云简化方法 杰魔提供了统一采样、格栅采样和曲率采样三种点云简化的处理方法，本研究采用统一采样的方式。通过调整统一采样的绝对间距，可以控制点云去除的数量。间距越大，点云去除数越多，保留的点数相应越少。待点云完成简化后，进行封装过程，设定封装的三角形数为简化后点数的1.5倍。封装完成后，运行网格医生和填充孔功能，保证封装无几何错误。以8号残片(左腿腿部)为例，该残片的原始点数目为27 893，对其进行从10%到80%的简化，则剩余点数和封装三角形数如表3所示。

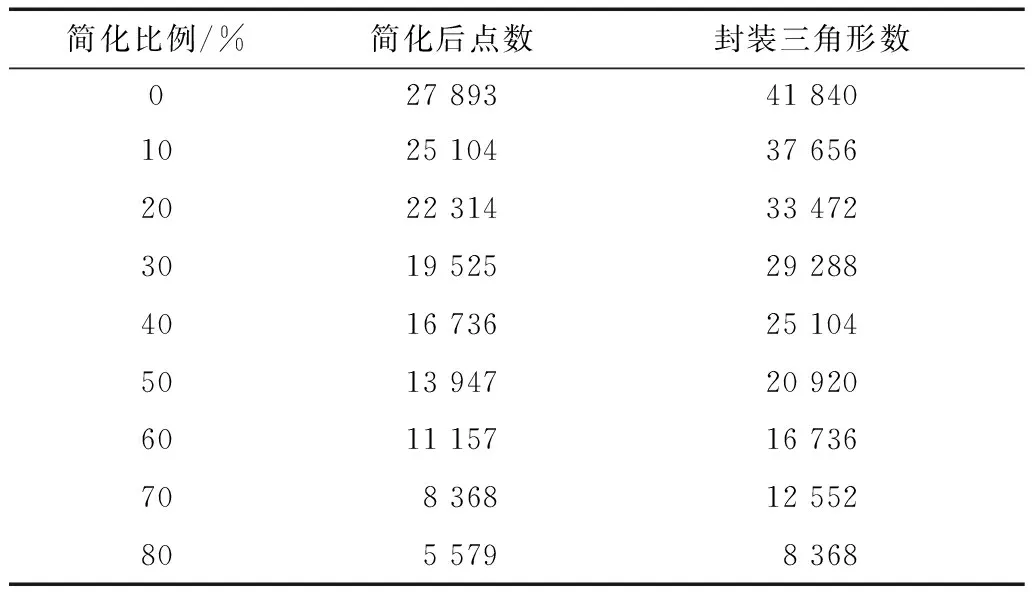
表3 8号残片简化对照表

2.2.2偏差分析 偏差分析可用于评估模型的准确性。在杰魔中，通常运用到以下4个指标进行偏差分析的评估：

1) 最大距离。即从分析体到参考体任意一点的最大偏差距离，分为正负两个方向[16]。

2) 平均距离。即从分析体到参考体上任意一点的平均偏差距离[16]。

3) 标准偏差S，表示偏差的离散程度[16]，可以反映数据的可靠性。即：

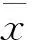
4)RMS，表示均方根，同样能够反映数据的可靠性：

式中，di为一组分析值与参考值的偏差[16]。

总之，小学语文教学中“儿童视野”的运用，不仅仅“师生关系”的调节剂，更是学生学习、教师进步的奠基石。用儿童视野看世界，能够收获不同的感受、能够看到不同的风景。每个孩子的想法不同，更需要教师耐心倾听，会对自己的教学，乃至日后的工作有非常大的帮助。

对于点云简化情况，相当于简化前后点个数不同。因此相比于最大距离和平均距离，采用标准偏差和RMS指标更能反映点数变化情况下模型的可靠性。本研究选取标准偏差指标作为偏差分析的评估参考。

对全部残片从10%～80%的比例进行简化，并统计每次简化后简化模型和参考模型之间的标准偏差值，该值可在软件中直接查看。各残片的标准偏差值与简化比例之间的关系如图4所示。

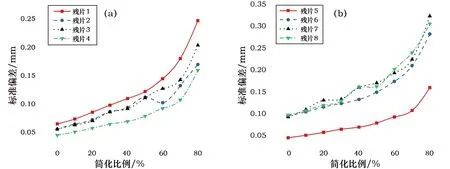
图4 不同点云简化比例下的标准偏差值

由图4可以看出，一般情况下，点云简化后的标准偏差随着简化比例的增加而增大。对于大部分残片，其曲线斜率在70%时发生显著变化，说明此时随着点数的进一步缩减，模型误差也在迅速增大。因而对于所有残片，其简化比例都应该控制在70%以内。对于残片8，简化比例在40%与50%的时候标准偏差接近，而在60%情况下偏差显著增大，因而该残片最优简化比例为50%；对于残片2，简化比例为60%的时候相比于50%的情况反而出现下降，因此该残片的最优简化比例为60%；对于其他残片，其最优简化比例在60%或70%，此时点云简化对偏差的增加影响较小。所有残片的最优简化比例如表4所示。其中，残片6由于在采用70%或60%的简化比例时后期出现曲面片错误，因而经调整后，其最优简化比例为40%。

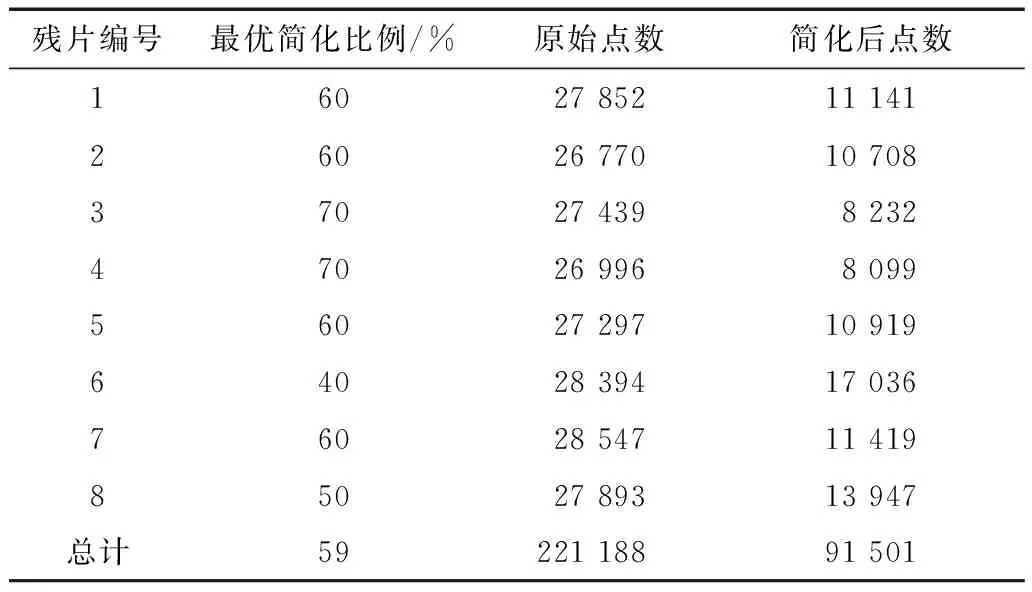
表4 各残片最优简化比例

对于各残片，在根据最优比例进行点云简化后，可以通过偏差分析云图观察简化后的效果。以8号残片为例，该残片最优简化比例为50%，简化后偏差分析云图如图5所示。从图中的数值信息可以看出，除标准偏差值与图4对应为0.161 3 mm以外，其最大偏差为±(1.256 4～1.071 5)mm，平均偏差为±(0.096 6～0.107 4)mm，RMS值为0.161 8mm，误差精度符合要求。从偏差云图形状可以看出，简化后的残片大部分颜色较为一致，且该颜色位于色谱中部，说明模型封装效果较好。对于其他残片，其数值信息和云图均满足精度要求。

图5 8号残片偏差分析云图

2.2.3点云简化前后模型处理时间比较 将原始点云残片和简化后的点云残片分别进行精确曲面过程，采用软件提供的自动曲面化功能，比较点云简化前后的处理时间。结果如表5所示，时间单位为s。可以看出，模型整体处理时间减少了51%。对于单一残片，除1号残片时间减少不明显外，其余残片的处理时间均缩减在35%以上。因此，点云简化对模型处理时间的缩短具有显著的意义。

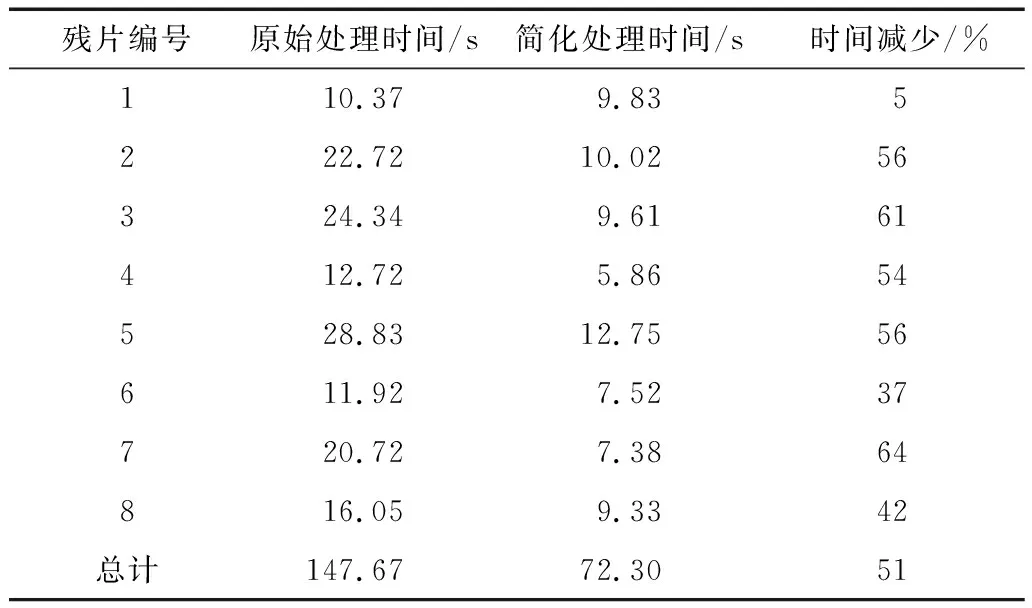
表5 点云简化缩减时间

2.2.4点云简化前后 有限元结果比较对于简化后的NURBS模型，在导入到Hypermesh进行网格划分时，同样设置网格种子尺寸为4，得到的四面体网格数为81 146。将简化前后各残片的模型体积进行比较，如表6所示。可以看出，模型简化后总体积相比于原始模型减少了0.37%，说明简化过程对模型的自身质量影响很小。

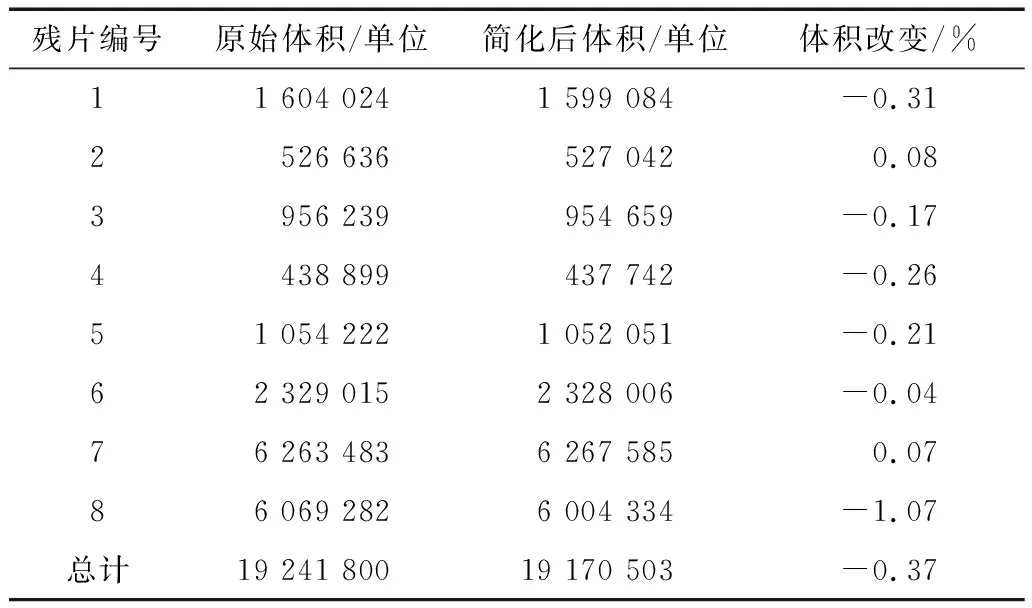
表6 点云简化前后模型体积比较

简化后模型的整体应力和变形如图6所示。与图3相比，应力方面，模型简化前后应力云图形状接近，且简化后的最大Mises应力同样位于左腿足踝处，为0.826 MPa，相比于原始结果误差为14%。变形方面，两者同样形状接近。可以看出，模型简化过程对计算结果影响较小，简化模型仍可较准确反映结构受力特征和规律。

图6 简化模型计算结果

3 结 论

本研究通过三维激光扫描对兵马俑残片进行了逆向建模，利用杰魔软件将点云模型实体化，再用Hypermesh将模型划分为四面体网格，从而在ABAQUS中进行有限元分析。进一步探究了点云简化对有限元分析结果的影响。得到的主要结论如下：

1) 原始未简化模型中，最大应力位于左腿足踝处，该最大应力远小于材料自身强度，说明结构在重力作用下处于安全稳定的状态。相比于左腿，右腿足踝处的最大应力较小，且右腿变形特征主要为竖向变形。而左腿的变形除竖向变形外还存在侧向变形。说明该俑的左腿为相对受力薄弱部位。

2) 对于本研究模型，根据偏差分析的结果，大部分残片最佳点云简化比例为60%～70%(即简化后保留30%～40%的点个数)。简化后模型实体化处理时间缩短了约50%，且模型的最大偏差处于精度要求范围内，简化后模型的总体积变化小于0.5%。说明该模型简化可在保证模型精度的前提下，有效缩短实体化处理的时间。

3) 采用点云简化模型进行有限元分析的结果，与采用原始点云模型相比，最大Mises应力误差小于15%，且应力云图和变形图形状基本一致。可以说明简化模型仍能较准确反映结构受力特征和规律。适当进行点云简化，可以有效节省建模时间，同时得到较为准确的结果。