离子径迹特征与纳米反相器链单粒子瞬态的关联性研究*

赵雯 陈伟 罗尹虹 贺朝会 沈忱

1) (西安交通大学核科学与技术学院, 西安 710049)

2) (西北核技术研究所, 强脉冲辐射环境模拟与效应国家重点实验室, 西安 710024)

3) (苏州珂晶达电子有限公司, 苏州 215000)

1 引 言

重离子单粒子效应(single event effects, SEE)实验通常采用线性能量传输值(linear energy transfer, LET)来量化沉积在器件敏感区的能量,这也是重离子SEE截面曲线以LET作为自变量的原因.然而, 不同能量和种类的离子可具有相同的LET值, 大多数重离子SEE地面模拟实验装置提供的离子能量在1—10 MeV·n—1, 少数重离子SEE地面模拟实验装置提供的离子能量在10—100 MeV·n—1, 但宇宙空间中重离子能量最高可至几百GeV·n—1, 峰值通量处的重离子能量也在几百MeV·n—1[1], 这意味着高能离子在宇宙空间中广泛存在, 地面重离子加速器可以提供与其LET值相当的离子, 但是能量偏低.已有研究表明[2-5], 相同LET值、不同能量和种类的重离子会导致器件的SEE响应存在差异, 这种差异与粒子径迹特征的差别有关联.Stapor等[2]用相同LET值、不同能量的离子辐照互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)工艺的晶体管, 发现高能离子导致的SEE电荷收集量更多, 与低能离子导致的电荷收集量差异最大可达60%左右.他们认为是高能离子径迹半径更大、径迹中心的载流子复合更少造成的.Dodd等[3]针对Sandia的一款绝缘体上硅工艺静态随机存取存储器(static random-access memory, SRAM)开展重离子实验, 发现在单粒子翻转(single event upset, SEU)截面曲线的高LET值区, 低能离子的截面比高能离子更大.他们认为是低能离子径迹的径向分布更紧凑、电荷收集效率(器件收集到的电荷量与离子在器件中沉积的电荷量的比值)更高所致.高丽娟等[4]对0.15 μm工艺的SRAM进行了重离子SEE测试, 发现在截面曲线接近饱和区的位置, 低能离子翻转截面比高能离子翻转截面大;而且通过Geant4模拟发现, 相同LET值条件下高能离子可在较远处沉积能量, 更易使同一存储单元内的相邻节点共享电荷, 引发单粒子翻转再恢复, 从而减小SRAM的SEU截面.Raine等[5]比较了相同LET值、不同能量和种类的重离子入射下, 70 nm部分耗尽绝缘体上硅工艺分立晶体管的SEE收集电荷差异, 发现低能离子导致更多的SEE收集电荷.他们认为高能离子径迹的径向宽度大于晶体管的敏感体积, 导致部分沉积电荷无法被有效收集, 而低能离子径迹的径向宽度小于晶体管的敏感体积, 沉积的电荷几乎全部对晶体管的单粒子响应产生贡献, 因此, 低能离子的电荷收集效率更高; 此外, 与高能离子相比, 低能离子入射导致的晶体管寄生双极放大增益更高, 这与低能离子径迹径向电荷分布更加紧凑有关.当器件特征尺寸减小到纳米尺度, 工作电压的降低和节点电容的减小使得SEE临界电荷变小, 相同LET值、不同能量和种类的离子入射纳米器件后, 在粒子径迹特征方面的较小差异可能会导致器件单粒子响应的明显不同.

在离子径迹特征与器件SEE的关联性研究中,晶体管SEE收集电荷和存储器SEU的相关研究占绝大多数[2-15], 组合逻辑电路单粒子瞬态(single event transients, SET)的相关研究未见报道.随着器件特征尺寸的减小和时钟频率的增加, 组合逻辑电路SET造成的软错误急剧增加并逐渐成为SEE软错误的主体[16-21], 开展离子径迹特征与纳米组合逻辑电路SET的关联性研究对准确预估纳米微电子器件在轨SEE软错误率具有重要意义.

本文以纳米CMOS工艺的体硅反相器链为研究载体, 结合TCAD (technology computer aided design)和Geant4耦合仿真, 研究了相同LET值的高低能离子的每核子能量比率、离子LET值、离子入射角度和反相器链偏置电压等参数对相同LET值的高低能离子所导致的纳米反相器链SET脉宽差异的影响, 从离子径迹特征与SET的内在关联角度对影响机制进行了分析.

2 TCAD模型的建立和离子径迹计算程序的开发

通过TCAD和Geant4耦合仿真开展研究, 其中TCAD软件Genius[22-24]用于纳米反相器链三维TCAD模型的构建及SET响应的计算, Geant4负责入射离子的输运模拟和离子径迹特征的提取.耦合仿真的基本思路是: 1)基于开源解析器minixml[25]建立Geant4和TCAD的接口程序, Geant4通过接口程序从TCAD模型中获取器件的几何结构及材料定义等参数, 并在Geant4环境中重构与TCAD仿真完全一致的几何模型[26]; 2)由于TCAD模拟采用四面体单元构建器件网格模型, 获取器件SET响应需要得到每个四面体元中的能量沉积, 这里利用Geant4开发相关程序, 对入射离子的随机输运过程进行跟踪模拟[27], 得到离子在各体元的能量沉积分布; 3)将各体元的能量沉积转换为SEE电荷产生率(见(1)式[28]), 把该产生率作为源项引入半导体方程组(包含泊松方程、漂移扩散方程以及载流子连续性方程), 通过有限元法求解方程组的数值解即可得到器件的SET响应[28].

其中,Edep为入射离子在四面体中沉积的能量,VTet为四面体体积,η= 3.6 eV (代表硅中产生一个电子-空穴对所需的能量),T(t) 为载流子时间分布的解析表达式.

2.1 TCAD模型的建立和校准

针对65 nm体硅CMOS反相器链建立TCAD模型, 考虑到电荷共享的存在, 反相器链选取为四级, 相应的电路原理图和TCAD模型如图1(a)和图1(b)所示.p型金属氧化物半导体(PMOS)晶体管和n型金属氧化物半导体(NMOS)晶体管的栅宽分别为0.32和0.24 μm, 栅长均为60 nm.晶体管的TCAD模型均通过电学特性校准, 即晶体管TCAD模型的I-V特性曲线与该晶体管HSPICE宏模型的I-V特性曲线一致, 如图2和图3所示.当反相器链的输入为逻辑低电平时, NMOS晶体管对SET敏感; 反相器链的输入为逻辑高电平时,PMOS晶体管对SET敏感.效应仿真中, 离子入射第一级反相器的敏感NMOS或者敏感PMOS,在第一级反相器的输出端产生瞬态脉冲, 该瞬态脉冲沿反相器链传播至输出端.仿真考虑的物理模型主要包括: 费米-狄拉克统计模型, 禁带变窄模型,Shockley-Read-Hall (SRH)复合和俄歇复合模型,考虑掺杂、电场和载流子浓度对迁移率影响的模型, 漂移扩散模型等.

图1 四级反相器链的(a)电路原理图和(b)三维TCAD模型Fig.1.(a) Schematic and (b) three-dimensional TCAD model of the 4-stage inverter chain.

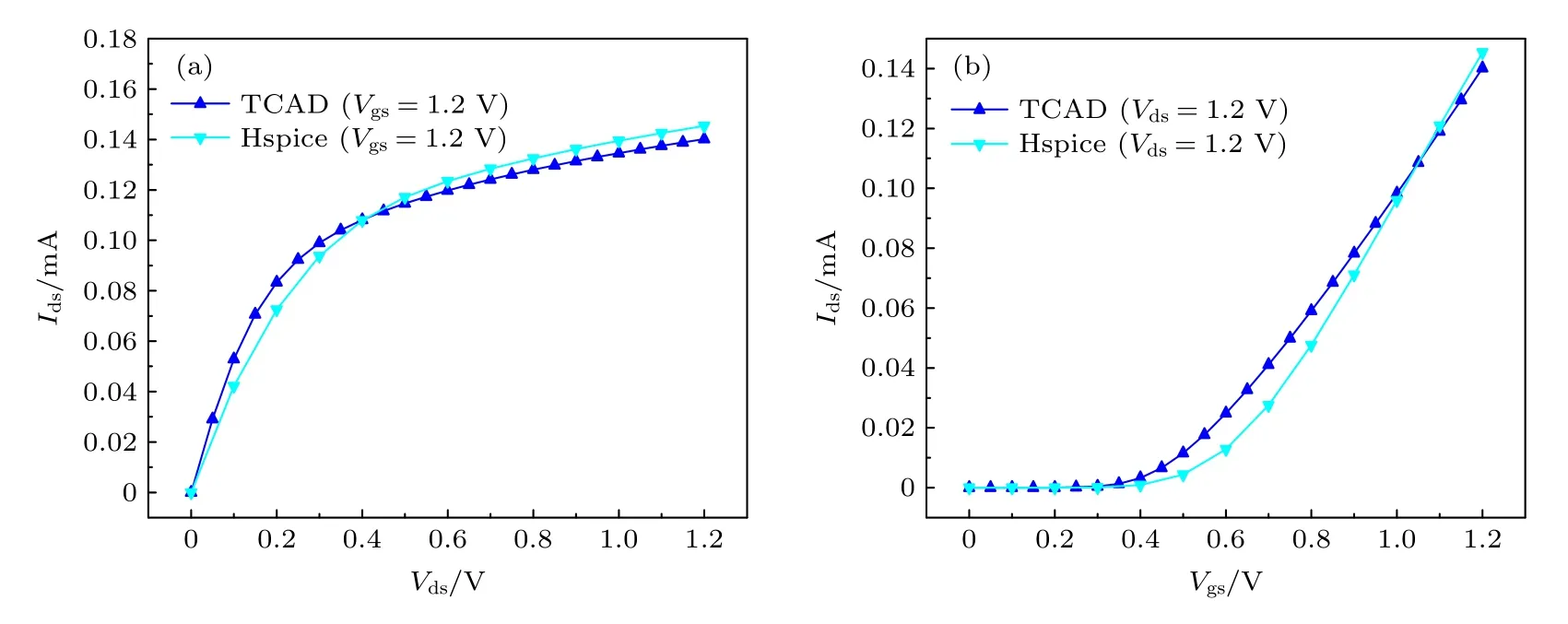
图2 NMOS晶体管的I-V特性校准 (a) Ids-Vds曲线; (b) Ids-Vgs曲线Fig.2.Calibration of I-V characteristics of the NMOS transistor: (a) Ids-Vds curves; (b) Ids-Vgs curves.

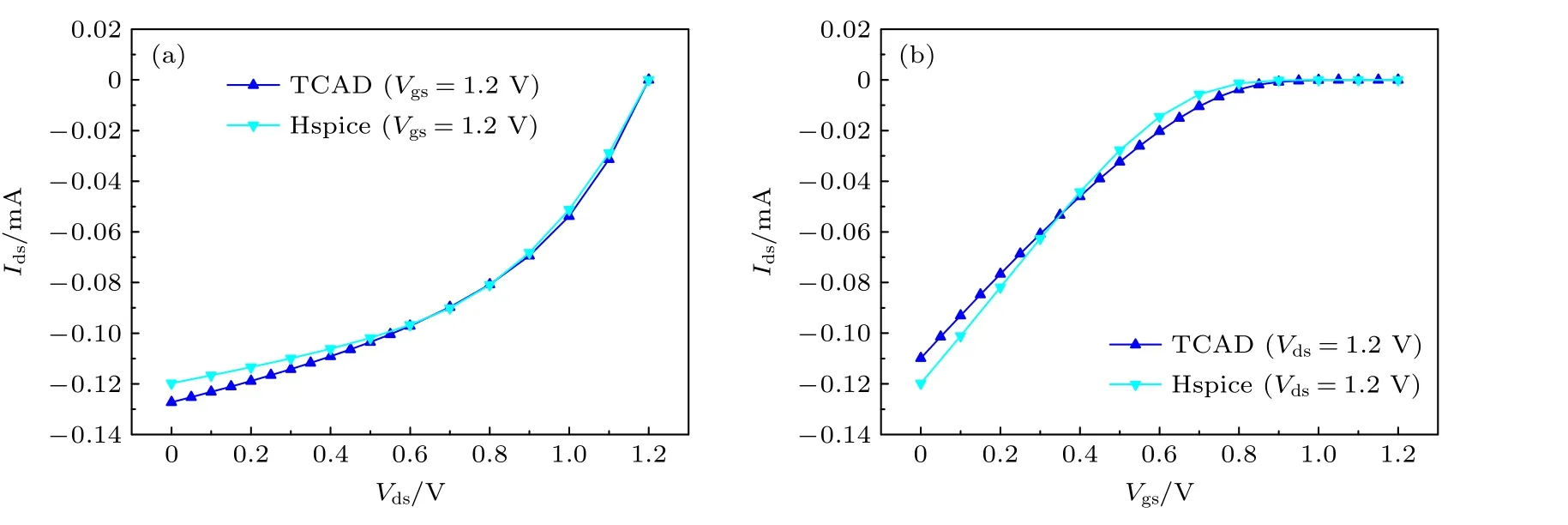
图3 PMOS晶体管的I-V特性校准 (a) Ids-Vds曲线; (b) Ids-Vgs曲线Fig.3.Calibration of I-V characteristics of the PMOS transistor: (a) Ids-Vds curves; (b) Ids-Vgs curves.

2.2 离子径迹计算程序的开发和结果验证

基于Geant4开发了离子径迹计算程序.Geant4的G4hIonisation类可以用来计算由于带电粒子本身电离损失的能量和次级粒子电离产生的离散式能量损失, 在仅考虑直接电离的情况下, 次级粒子主要是电子, 对于电子与材料相互作用过程的描述选用G4EmLivermorePhysics模型, 在该模型中包括光子、电子和正电子的一系列物理过程, 如康普顿散射、光电效应、韧致辐射和正电子湮灭等.离子径迹计算程序旨在获取离子径迹的径向能量沉积分布.考虑到能量沉积围绕径迹中轴线(中轴线由离子入射位置和入射方向共同决定)呈径向对称, 在计算能量沉积分布时, 以径迹中轴线为中心设置一系列同轴圆柱壳, 圆柱壳的半径从内向外依次增大[29], 相邻圆柱壳围成具有一定径向厚度的圆筒状敏感探测器, 敏感探测器相对于径迹中轴线的径向距离为内圆柱壳和外圆柱壳半径的平均值.为减小各敏感探测器内能量沉积的统计误差, 令1000个离子沿相同方向从同一位置入射硅材料,统计每一个敏感探测器内的能量沉积, 然后除以相应敏感探测器的体积得到能量沉积密度, 再除以1000归一化到单个离子的能量沉积密度, 该能量沉积密度所对应的沉积位置由敏感探测器相对于径迹中轴线的径向距离来表征, 如此就可以得到单个离子的能量沉积密度随离子径迹径向尺度的变化.有时在离子径迹计算时, 会将能量沉积密度转化为电子-空穴对密度(离子在硅材料中每沉积3.6 eV的能量可产生一个电子-空穴对).

将本文中用Geant4计算的23 MeV·n—1Kr 离子的径迹数据与文献[30]用Geant4计算的离子径迹数据进行了比较, 这里的径迹数据是指离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化.本文和文献[30]均采用G4EmLivermorePhysics模型处理次级电子的输运过程, 对比结果如图4所示.可以看出, 两者计算的离子径迹数据符合较好, 证明了离子径迹计算程序的可靠性.值得一提的是, 文献[30]未提供敏感探测器的设置、粒子射程截断值等物理模型参数的选取信息, 本文在进行对比计算时无从参照, 这可能是造成两径迹数据略微存在差异的原因.

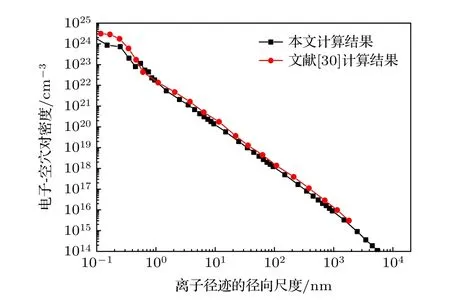
图4 本文和文献[30]通过Geant4计算得到的23 MeV·n—1 Kr离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化Fig.4.Density of electron-hole pairs generated by 23 MeV·n—1 Kr ion incidence into silicon vs.the radial scale of ion track, which are calculated by Geant4.The calculated data of our work and Ref.[30] are compared.

3 研究结果及分析

仿真用到的重离子的详细信息如表1所列.离子分为三组, 三组的LET值依次增大.每一组中的离子在硅表面的LET值相同, 但离子能量和种类不同, 其中每核子能量小于10 MeV的离子为低能离子.第一组离子中, 低能离子为5.3 MeV·n—1的Si离子, 高能离子为83.3 MeV·n—1的Kr离子.第二组离子中, 低能离子为3.8 MeV·n—1的Ti离子, 而高能离子为66.7 MeV·n—1的Xe离子以及150.3 MeV·n—1的Ta离子.第三组中, 低能离子为3.4 MeV·n—1的Br离子, 高能离子为50.3 MeV·n—1的Ta离子.

表1 重离子的详细信息Table 1.Detail information of the heavy ions.

图5所示为Geant4计算得到的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化.可以看出, 同一组离子中的高能离子的径迹半径为低能离子径迹半径的数倍; 在1—10 nm的径向尺度内, 低能离子产生的电子-空穴对密度明显大于高能离子, 最大差异超过1个数量级; 而在小于零点几纳米的径向尺度内, 高能离子产生的电子-空穴对密度高于低能离子.上述规律与文献[5]通过Geant4计算得到的高低能离子径迹数据的对比结果在趋势上是一致的.

图5 Geant4计算得到的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化 (a) 第一组高低能离子; (b)第二组高低能离子; (c)第三组高低能离子Fig.5.Density of electron-hole pairs generated by ion incidence into silicon vs.the radial scale of ion track: (a) The first group of ions; (b) the second group of ions; (c) the third group of ions.

仿真中, 离子入射位置分布在第一级反相器的有源区(图6), 让离子依次入射图6所示的位置,记录每一个入射位置所对应的反相器链输出端的SET脉宽(半高宽)Wout, 然后比较高低能离子在每一个入射位置上的Wout差异δ(δ等于低能离子的Wout减去高能离子的Wout), 最后将δ在不同入射位置上的数值通过统计图显示出来.

图6 离子入射位置示意图(*表示入射位置)Fig.6.Schematic diagram of ion strike locations, where *indicates the ion strike locations.

3.1 高低能离子每核子能量比率的影响

第二组的Ti离子为低能离子, Xe和Ta均为高能离子, Xe离子与Ti离子的每核子能量比率约为17.5, 而Ta离子与Ti离子的每核子能量比率更高, 约为39.5.图7(a)为Ti离子与Xe离子的脉宽差异δ随入射位置的分布, 图7(b)为Ti离子与Ta离子的脉宽差异δ随入射位置的分布.离子垂直入射, 反相器链偏置电压为1.2 V.图中X坐标为离子入射位置在沿阱方向的坐标,Y坐标为离子入射位置在垂直阱方向的坐标,Z轴物理量为脉宽差异δ, 图中红色柱代表δ等于0, 黑色柱代表δ小于0, 灰色柱代表δ大于0, 柱的高低代表δ的数值大小.通过对比发现, 不同入射位置上Ti离子与Xe离子的脉宽差异绝对值均小于50 ps, 但Ti离子与Ta离子的脉宽差异的绝对值最大可达到157 ps.此外, 计算了各入射位置脉宽差异δ的平方和Σ, 发现图7(a)脉宽差异δ和图7(b)脉宽差异δ的平方和分别为14796和47079.综上, 高低能离子的每核子能量比率越大, 脉宽差异越明显.通过图5(b)可以看出, 150.3 MeV·n—1的 Ta离子与3.8 MeV·n—1的Ti离子的电子-空穴对密度在径迹中心轴附近区域的差异比66.7 MeV·n—1的Xe离子与3.8 MeV·n—1的Ti离子的电子-空穴对密度在径迹中心轴附近区域的差异更加明显.径迹中心轴附近区域的电子-空穴对密度的差异越明显,电子-空穴对的复合差异就越大, 从而使后续的电荷收集量存在较大差别, 这应该是导致高低能离子的每核子能量比率越大脉宽差异越明显的原因.

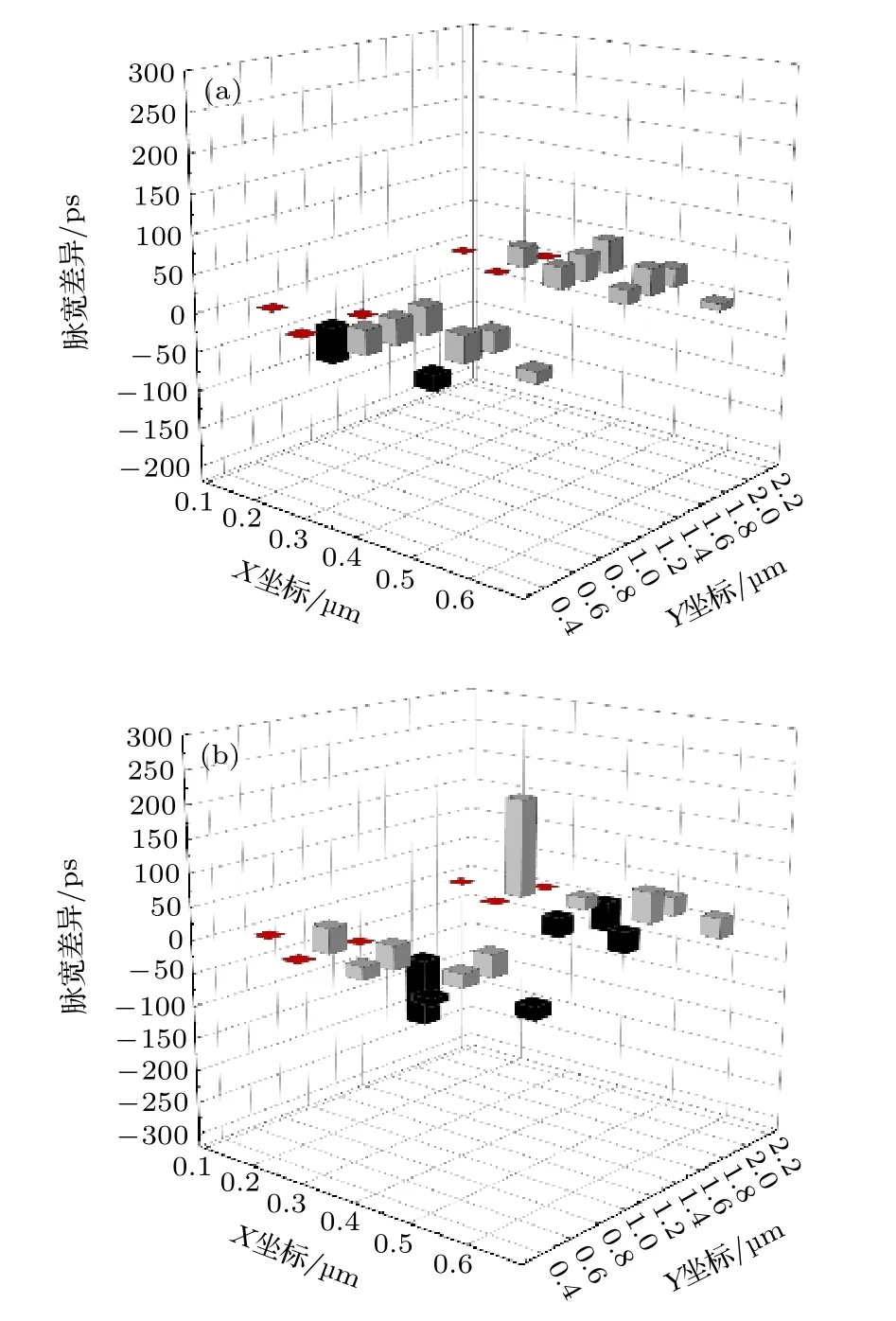
图7 第二组高低能离子导致的瞬态脉宽差异在不同入射位置上的分布 (a)第二组离子Ti和Xe的比较; (b)第二组离子Ti和Ta的比较Fig.7.Distribution of the transient pulse width differences at various strike locations for the second group of ions:(a) Low- and high-energy ions are Ti and Xe respectively;(b) low- and high-energy ions are Ti and Ta respectively.

3.2 离子LET值的影响

接下来比较三组离子的脉宽差异分布, 结果如图8所示.其中第二组离子选取Ti和Xe离子, 以保证高低能离子每核子能量比率尽量与其他两组接近.对于第一组离子(LET = 8.8 MeV·cm2·mg—1),多数入射位置下的脉宽差异为0 ps; 对于第二组离子(LET = 21.3 MeV·cm2·mg—1), 多数入射位置下都存在脉宽差异, 但脉宽差异的绝对值均小于50 ps; 而对于第三组离子(LET = 41.4 MeV·cm2·mg—1), 基本所有入射位置下都存在脉宽差异,且脉宽差异的绝对值最大可达到262 ps.此外, 三组高低能离子的脉宽差异的平方和Σ分别为6832, 14796和153339.因此, 随着LET值的增大,相同LET、不同能量和种类的离子所导致的脉宽差异逐渐明显.将高低能离子每核子能量比率基本一致的三组离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化统一示于图9, 可以看出, 在相同径向尺度上, 随着LET值的增大, 高低能离子所产生的电子-空穴对密度的差异逐渐增大(纵坐标为对数坐标), 这将导致高低能离子在电路敏感区及周围的电荷沉积差异更大, 进而使得脉宽差异更明显.

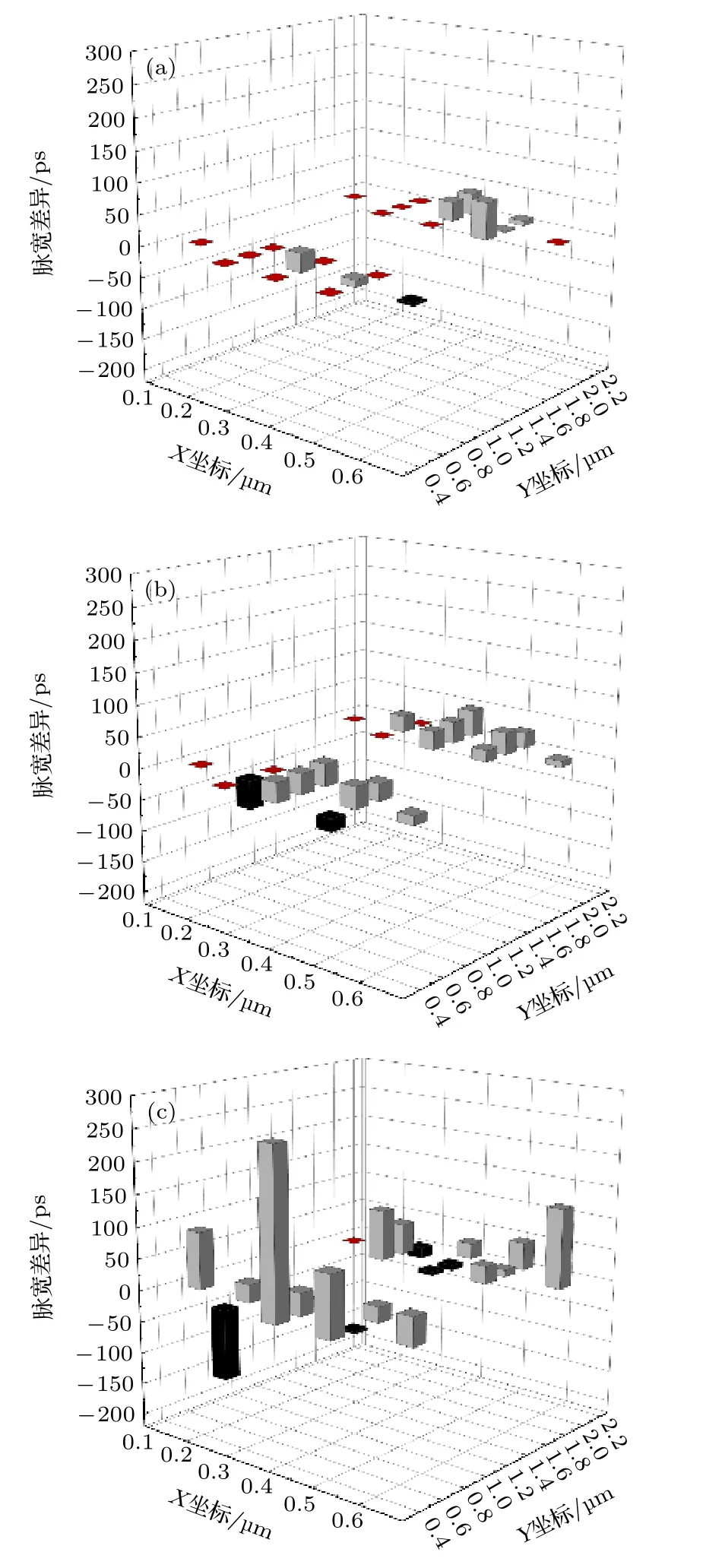
图8 三组高低能离子导致的瞬态脉宽差异在不同入射位置上的分布 (a)第一组离子Si和Kr的比较; (b)第二组离子Ti和Xe的比较; (c)第三组离子Br和Ta的比较Fig.8.Distribution of the transient pulse width differences at various strike locations: (a) Comparison of Si and Kr ions in the first group; (b) comparison of Ti and Xe ions in the second group; (c) comparison of Br and Ta ions in the third group.

图9 每核子能量比率接近的三组高低能离子入射硅材料生成的电子-空穴对密度随离子径迹径向尺度的变化Fig.9.Density of electron-hole pairs generated by ion incidence into silicon vs.the radial scale of ion track.The energy per nucleon ratios of high-energy ion to low-energy ion are similar for the three groups.

3.3 离子入射角度的影响

图10 所示为第三组的Br和Ta离子在不同入射角度下(沿阱方向30°入射、沿阱方向60°入射、垂直阱方向30°入射、垂直阱方向60°入射)的脉宽差异分布, 表2统计了两种离子在不同入射角度下的脉宽差异的平方和.通过对比发现, 沿阱方向斜入射的脉宽差异比垂直阱方向斜入射的脉宽差异更加明显.垂直阱斜入射时, 随着入射角度从30°增加到60°,Σ值从13765变为14131, 两者差别不大.然而, 沿阱方向斜入射时, 随着入射角度从30°增加到60°,Σ值从93602增加到161159,两者差别明显, 且沿阱方向60°斜入射与沿阱方向30°斜入射相比, 在更多的入射位置上出现了高能离子脉宽较大的现象(δ小于0).下面将通过TCAD仿真来研究沿阱方向30°和60°斜入射的差异.

表2 第三组的Br和Ta离子在不同入射角度下导致的瞬态脉宽差异平方和Table 2.Square sum of the transient pulse width differences at various strike locations for the Br and Ta ions in the third group at different ion incidence angles.

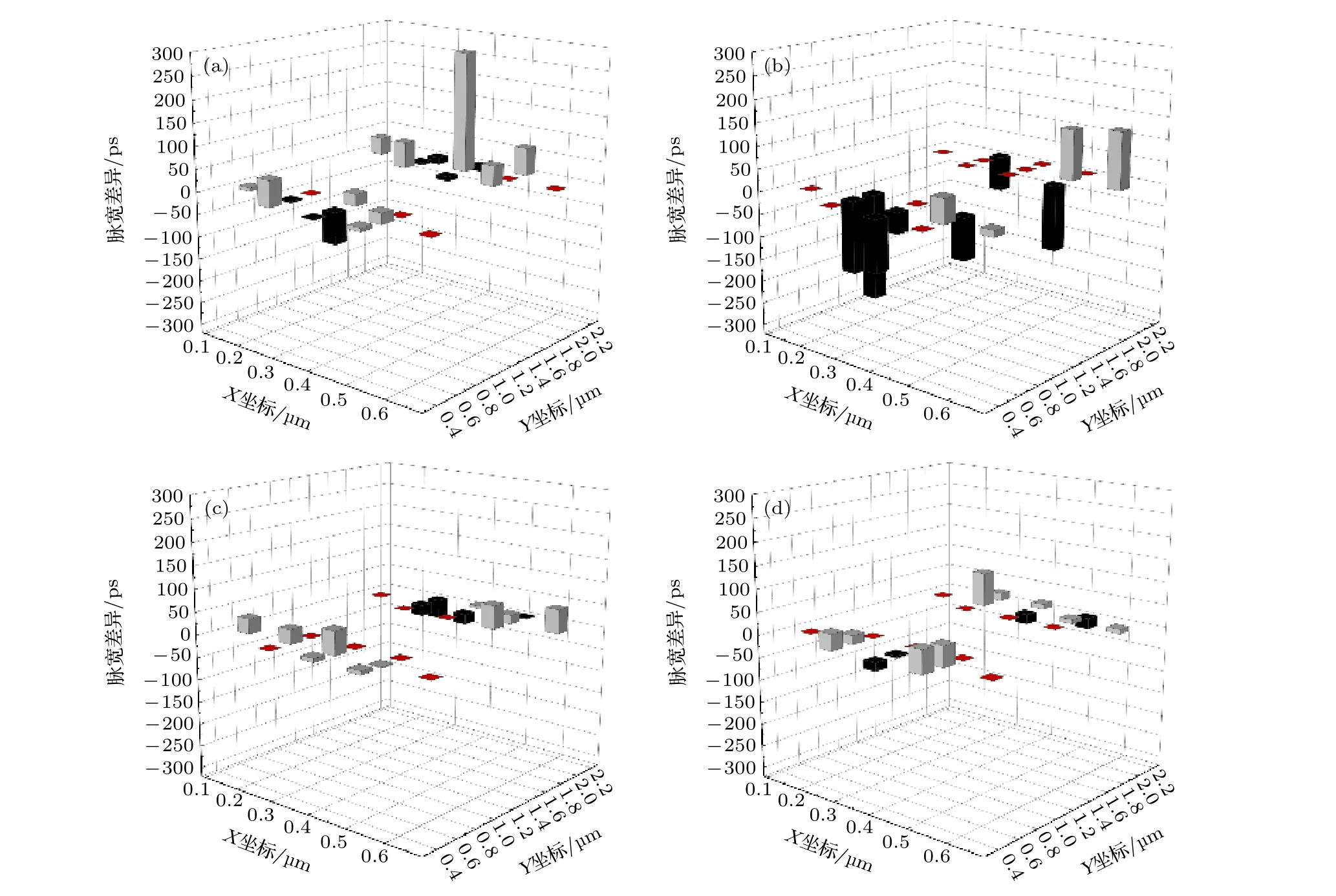
图10 第三组的 Br和Ta离子在不同入射角度下导致的瞬态脉宽差异随入射位置的变化 (a)沿阱方向30°入射; (b)沿阱方向60°入射; (c)垂直阱方向30°入射; (d)垂直阱方向60°入射Fig.10.Distribution of the transient pulse width differences at various strike locations for the Br and Ta ions in the third group at different ion incidence angles: (a) 30° along the well; (b) 60° along the well; (c) 30° across the well; (d) 60° across the well.

图11 所示为Br和Ta离子沿阱方向30°入射第一级反相器NMOS漏极附近位置(0.51 μm,0.77 μm)时, 反相器链各级输出端的SET波形;图12所示为Br和Ta离子沿阱方向60°入射第一级反相器NMOS漏极附近位置(0.51 μm, 0.77 μm)时, 反相器链各级输出端的SET波形.可以看出,离子沿阱方向30°入射时, 随着入射深度的增加,径迹开始远离反相器的有源区, 后三级反相器收集电荷很少, SET波形受电学屏蔽的影响从第一级反相器输出端开始逐级消减, 到第四级时SET几乎消失.两离子的效应规律类似, 最终的SET脉宽基本没有差异.离子沿阱方向60°入射时, 两离子在第一级反相器输出端的SET脉宽略有差异,Br离子导致的SET脉宽稍小, 这可能与Br离子径迹中心轴附近区域的电子-空穴复合率较高有关;第二级反相器由于脉冲淬熄效应导致输出端SET脉冲基本消失; 第三级反相器通过收集斜入射径迹的扩散电荷而产生SET脉冲, 两离子诱发的SET脉宽相近; 在第四级反相器, Br离子斜入射产生的脉冲淬熄比Ta离子更严重, 最终导致Br离子的SET脉宽较小.之所以Br离子在第四级反相器的脉冲淬熄更严重, 是因为随着离子径迹向远端反相器下方延伸, 径向电荷分布紧凑的低能Br离子比径向电荷分布较松散的高能Ta离子的电荷收集效率更高, 导致低能Br离子在第四级反相器处的电荷共享更明显.通过沿阱方向30°和沿阱方向60°的仿真对比发现, 离子入射角度的变化导致电荷收集过程存在差异.

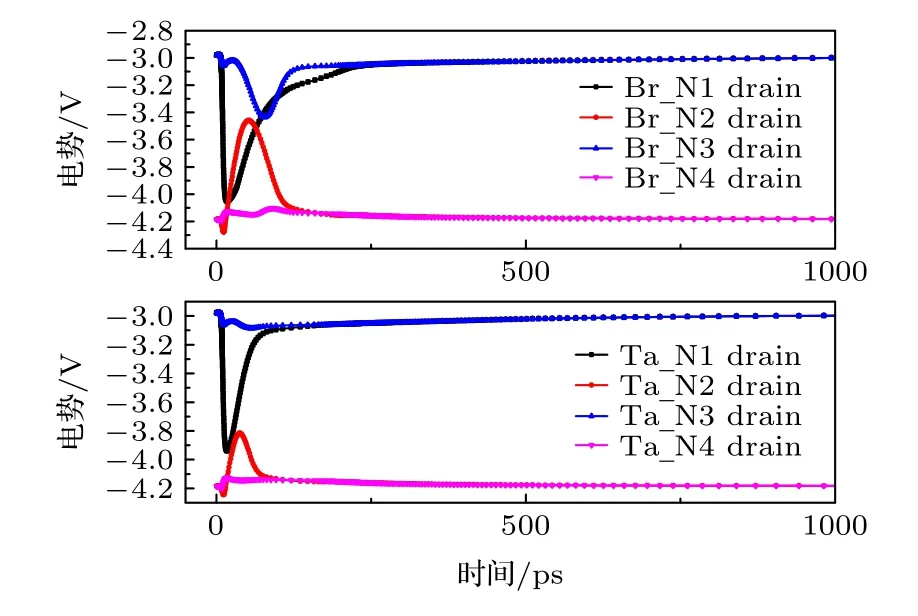
图11 第三组的Br和Ta离子沿阱方向30°入射(0.51 μm,0.77 μm)时, 反相器链各级输出端的SET波形Fig.11.Transient waveforms for N+-drains of the inverter chain, which are induced by Br and Ta ions in the third group.The ion incidence angle is 30° along the well.The strike location is with the coordinate of (0.51 μm, 0.77 μm).

图12 第三组的Br和Ta离子沿阱方向60°入射(0.51 μm,0.77 μm)时, 反相器链各级输出端的SET波形Fig.12.Transient waveforms for N+-drains of the inverter chain, which are induced by Br and Ta ions in the third group.The ion incidence angle is 60° along the well.The strike location is with the coordinate of (0.51 μm, 0.77 μm).

相同LET值的高低能离子入射纳米反相器链后在电荷产生方面存在差异, 离子入射角度的变化导致电荷收集过程存在差异, 两种差异的相互耦合决定了相同LET值的高低能离子的脉宽差异存在一定的离子入射角度依赖性.

3.4 反相器链偏置电压的影响

选取第二组的Ti和Xe离子, 为反相器链设置1.0, 1.2和1.4 V的偏置电压, 比较不同偏置电压下高低能离子的脉宽差异, 结果如图13所示.可以看出, 相同LET值的高低能离子导致的脉宽差异没有表现出明显的偏置电压依赖性, 且通过计算发现, 1.0, 1.2和1.4 V偏置电压下, 高低能离子的脉宽差异的平方和分别为17322, 14796和15583,也未呈现出明显的偏置电压相关性.

从宏观角度来看, 偏置电压的改变会影响被入射反相器的开态晶体管的驱动电流, 随着偏置电压的升高, 开态晶体管的驱动电流增大, SET脉宽减小, 但这一影响机制与离子径迹无直接关联.从微观角度来看, 偏置电压会影响反相器有源区的电场分布, 由于高低能离子入射反相器所产生的电子-空穴对分布存在差异, 该差异导致电子、空穴后续的输运和收集过程受电场分布变化的影响会有所不同, 这种影响机制与离子径迹存在关联, 但从图13的仿真结果来看, 在绝大多数离子入射位置上, 这种关联性并不明显, 考虑是偏置电压变化量太小(纳米反相器链在实际工作中, 其偏置电压的可调节范围十分有限), 不足以将电场分布变化所带来的影响呈现出来.

图13 不同偏置电压下, 第二组的Ti和Xe离子导致的瞬态脉宽差异随入射位置的变化Fig.13.Transient pulse width differences under different supply voltages vs.the strike location for the Ti and Xe ions in the second group.

4 讨 论

对于相同LET值的高低能离子入射硅材料而言, 两者在径迹中心轴10 nm径向尺度范围内的电子-空穴对密度存在明显差异, 虽然该尺度范围相对于离子的径迹半径(微米量级)而言很小, 但在离子径迹形成早期, 由于径迹中心轴附近区域载流子浓度很高, 部分电子-空穴对发生复合, 同时,该区域产生快速内部电场[31], 电场对低能次级电子造成陷阱效应, 这些微观机制直接影响SET的电荷收集量.高低能离子在径迹中心轴附近区域的电子-空穴对密度的差异, 造成了电子-空穴对复合率和快速内部电场的变化, 导致SET电荷收集量的不同, 最终反映在SET脉宽的差异上.此外, 对于相同LET值的不同高能离子入射硅材料而言,径迹结构差异主要体现在径迹中心轴1 nm径向尺度范围内, 通过3.1节的仿真结果不难看出, 即使在如此小的径向尺度范围内存在电子-空穴对密度的差异, 也会导致SET脉宽的不同, 说明径迹中心轴附近区域的电子-空穴对微观演化机制在离子径迹特征对纳米组合逻辑电路SET的影响中发挥重要作用.

在LET值相同的情况下, 高能离子的径迹半径是低能离子径迹半径的数倍, 若纳米组合逻辑电路对SET非常敏感且相邻敏感单元之间的间距很小, 高能离子更大的径迹覆盖范围将可能导致电路多个敏感单元收集电荷, 产生单粒子多瞬态, 而低能离子可能由于径迹半径较小只产生单个瞬态脉冲; 若纳米组合逻辑电路对SET不太敏感或者相邻敏感单元之间的间距不够小, 高低能离子径迹覆盖范围的差异不会对纳米组合逻辑电路SET产生明显影响.

5 结 论

以65 nm体硅CMOS反相器链为研究载体,基于TCAD和Geant4耦合仿真, 从离子径迹特征与SET的关联性出发, 研究了相同LET值、不同能量和种类的离子所导致的SET脉宽差异, 其中低能离子能量小于10 MeV·n—1, 高能离子能量介于几十MeV·n—1和几百MeV·n—1之间.结果显示: 具有相同LET值的高低能离子的每核子能量比率越大, 两者在径迹中心轴附近的电子-空穴对密度差异越大, SET脉宽差异越明显; 在高低能离子的每核子能量比率相近的情况下, LET值较大的高低能离子在相同径迹径向尺度上所产生的电子-空穴对密度的差异较大, SET脉宽差异更显著;离子径迹特征对纳米反相器链SET的影响存在一定的离子入射角度依赖性, 但与反相器链偏置电压的相关性不强.本研究工作为航天器用纳米微电子器件在轨单粒子效应软错误率预估提供支撑.