高中数学培养学生数学抽象素养的策略探究——以人教A版数学必修第一册函数的概念教学为例

文/中山市濠头中学 乔爽丽

数学是研究客观世界数量关系和空间形式的科学，其学科本质是让学生理解数学概念，把握数学思想，感悟数学思维，追求数学精神。数学学科的核心素养是高中阶段学生育人价值的集中体现，是学生在中学阶段需要的必备品格和关键能力。在新课标要求下，数学抽象在高中数学六大核心素养中有重要地位。

高中数学抽象素养的主要任务是:引导学生用数学的眼光看待生产生活、社会中的活动经验和具体问题，运用数学的知识和方法进行思考，把握事物的数学本质，能高度概括、表达准确地抽象出数学问题，用数学语言或者数学符号表述出来并加以解决，逐步养成理性思考问题的习惯，从而更好解决问题。

函数是描述变量间依赖关系的重要数学模型。用集合和对应的语言更清楚地表达函数的概念，有助于我们正确认识函数、理解函数和运用函数解决问题。函数概念是新人教A 版数学必修第一册第三章“函数的概念与性质”中第一节。本节课主要蕴含了数学抽象、逻辑推理、数学运算、直观想象四大核心素养，是高中学习函数的起始课。作为中学阶段数学课程的一条主线，函数内容的安排体现了数学概念抽象的层次性。第一个层次，作为第一册第三章内容，它是对第一章集合内容的巩固和发展。第二个层次，高中函数学习具有系统性，与后面三角函数、数列、方程、不等式、导数、解析几何等内容存在密切联系。现代，函数的应用已经渗透到数学、计算机科学、自然科学乃至人文科学的各个领域中了。在计算机程序语言中，函数概念有了很大拓展并得到了充分应用。特别是在某些人工智能语言中，几乎所有的操作都用函数来表示。因此，在函数概念教学中加强学生数学抽象素养的培养，是高中阶段数学学科的必然要求。

一、情境设计，抽象数学问题

教科书60 页首先回顾了初中阶段学生学习的函数的定义。然后引出情境设计:“正方形的周长l 与边长x 的对应关系式是l =4x，而且对于每一个确定的x都有唯一的l 与之对应，所以l 是x 的函数. 此函数与正比例函数y =4x 是否相同?又如，你能用初中学过的函数知识判断y =x 与是否相同吗?”如果学生要回答这些问题，需要对函数的概念再认识。

通过适当的问题设置，让学生体会到，由于知识储备有限，利用初中所学函数定义回答这些问题有困难，需要对函数概念有更高层次的解释和理解. 需要从根本上揭示函数的本质。重新从集合和对应的语言更清楚来表达函数的概念。

二、归纳探索，抽象函数概念

新人教A 版数学必修第一册教科书60 －62 页，问题1 是运动中的路程问题，以解析式呈现。通过问题设置激发学生认知上的冲突，发现初中函数概念“变量说”的不严谨、不完整性，使学生体会用集合语言和对应关系重新定义函数的必要性。在教师的引导下，给出了用更高层次的数学语言抽象具体问题中对应关系的示范。为后续三个实例做铺垫，在变化的情境中引导学生用同样的语言描述相应的变量关系和规律，从而形成归纳、概括概念的素材。

第2 个问题属于经济生活问题，教科书中是用解析式呈现。通过问题2，学生能锻炼抽象概括能力，知道函数的三个要素能完全确定一个函数。

第3 个问题属于自然界情境问题，教科书中是用图像呈现的。学生在理解图像呈现的函数时会出现困难，特别是当函数值的集合和函数值所在的集合不一样时，从而增强用抽象符号表示函数的必要性。

第4 个问题属于生活问题情境，教科书中是用表格呈现的。使学生注意到函数的对应关系不仅可以用解析式、图像表示，还可以用表格表示，为抽象出函数的对应关系f 做铺垫，让学生进一步体会到函数的三个要素的意义，也再次让学生体会函数值的集合和函数值所在的集合是不同的。

通过上述问题1 ～问题4 中的函数的共同特征，回顾用集合与对应语言刻画函数的过程，引导学生以表1的形式抽象出函数的本质特征。

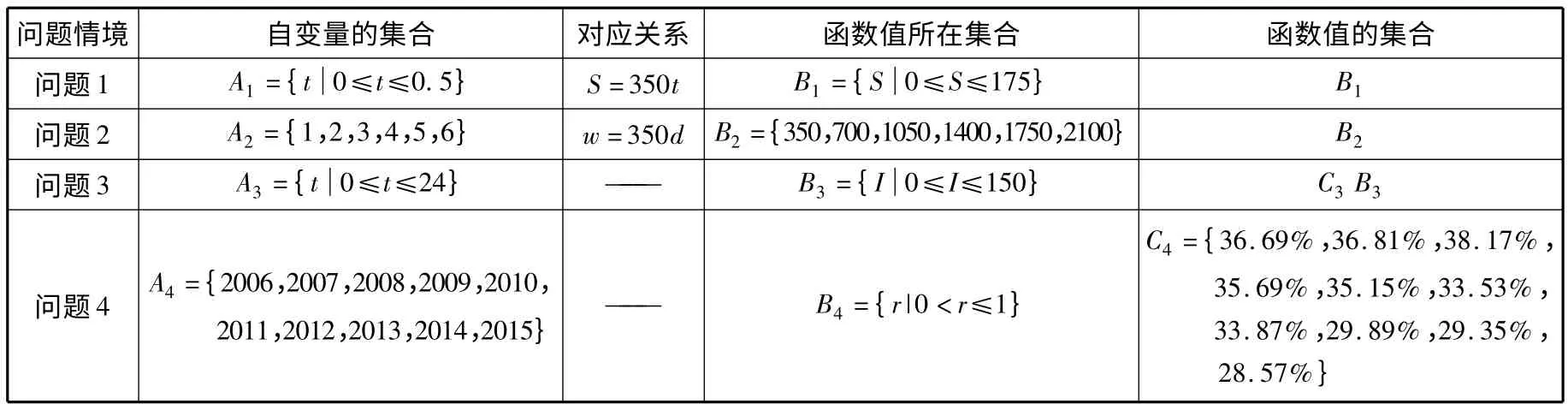
表1 函数特征表

引导学生对4 个问题归纳、概括，从而得出函数的3 点共同特征:①都有两个非空的实数集，我们用A，B来表示;②都有一个对应关系;③虽然4 个问题中对应关系的表示方法不同，但都有一个共同的特征:一个数集到另一个数集的一种确定的对应关系。对于数集A中的任意一个数x，按照对应关系，在数集B 中都有唯一确定的数y 和它对应。

由上面的共同特征，抽象出函数的一般性定义。强调函数的对应关系不仅可以用解析式、图像表示，还可以用表格表示，在高中数学定义中，我们引进用抽象的符号f 来表示对应关系。

三、巧用数学抽象符号y =f(x)，理解数学抽象内涵

在认识了函数自变量与函数值这两个要素后，如何理解函数的对应关系成为很关键的教学问题。在教学中，引导学生通过四个问题的分析，在解析式、图像和表格中认识并抽象出函数的对应关系。对于数学抽象符号y = f(x)，很多学生不理解函数符号的意义。1797 年，法国数学家拉格朗日指出:“我们用字母 f 或者F 放在一个变量前面以表示该变量的一个函数，即表示依赖于这个量的另一个量，它按一种给定的规律随那个变量一起变化”。当自变量为x 时，f(x)表示对应的唯一确定的函数值，并不表示f 与x 的乘积。此处的抽象符号f 实际上是一种对应关系，在题目中可以是解析式，也可以是图像或者图表来呈现。

四、类比联想，促进学生数学抽象素养

用这个新的函数定义，引导学生重新认识初中学过的三类函数，如表2 所示。

表2 函数类形表

让学生用新的语言描述学过的函数，既可以熟悉新概念，又能和旧的概念做比较，感受“集合—对应说”函数概念的严谨性，从而促进数学抽象素养培养。

五、概括演练，提升学生的数学抽象

例题:试构建一个问题情境，使其中的变量关系可以用解析式y=x(10 －x)来描述。

我们把y =x(10 －x)看成一个二次函数，那么它的定义域就是R，值域是对应关系f把R 中的任意一个数x 对应到B 中唯一确定的数x(10 － x)。

构建问题情境，解析函数y =x(10 －x)的对应关系，这是一个从抽象到具体的过程，也可以看成是不同表示方式之间的相互转换，可以使学生体会函数的三要素，以及一个一般抽象函数表达式的广发适用性，从而提升学生的数学抽象思维。