基于粒子群优化算法和长短时记忆神经网络的蟹塘溶解氧预测

任妮 鲍彤 刘杨 荀广连 蒋永年

摘要： 为准确预测蟹塘溶解氧质量浓度，及时掌握溶解氧质量浓度的变化趋势，提前采取防控措施从而降低河蟹养殖风险，提出了一种基于粒子群优化算法（PSO）和长短时记忆神经网络（LSTM）的蟹塘溶解氧质量浓度预测模型，采用PSO算法优化LSTM模型参数后对蟹塘溶解氧质量浓度进行预测。结果表明，PSO-LSTM模型不仅整体优于ARIMA模型，相较于其他LSTM模型也有更高的预测精度，在连续10个时间点的预测中相比于LDO-LSTM、LSTM和ARIMA模型平均百分误差分别降低了2.55%、1.891%和4.055%。说明PSO-LSTM模型在蟹塘溶解氧质量浓度预测中具有良好的准确性和稳定性，可以为河蟹养殖中水质精准预测与调控提供参考。

关键词： 溶解氧预测;河蟹养殖;粒子群优化算法;长短时记忆神经网络

中图分类号： S126  文献标识码： A  文章编号： 1000-4440（2021）02-0426-09

Abstract： To predict the mass concentration of dissolved oxygen in Chinese mitten crab ponds accurately， grasp the changing trend of the mass concentration of dissolved oxygen timely and take preventive and control measures in advance to reduce the risk in Chinese mitten crab culturing， a model for predicting the mass concentration of dissolved oxygen in Chinese mitten crab ponds based on particle swarm optimization （PSO） and long short-term memory （LSTM） neural networks was proposed. The mass concentration of dissolved oxygen in Chinese mitten crab ponds was predicted after optimizing LSTM model parameters by PSO algorithm. The results showed that the PSO-LSTM model was not only superior to the ARIMA model， but also had higher prediction accuracy compared with other LSTM models. In the predictions at 10 consecutive time points， the average percentage error of the PSO-LSTM model reduced by 2.55%， 1.891% and 4.055% respectively， compared with the LDO-LSTM， LSTM and ARIMA models. It can be seen that the PSO-LSTM model has good accuracy and stability in the prediction of the mass concentration of dissolved oxygen in Chinese mitten crab ponds， and can provide a reference for accurate prediction and regulation of water quality in Chinese mitten crab culturing.

Key words： prediction of dissolved oxygen;culturing of Chinese mitten crab;particle swarm optimization algorithm;long short-term memory neural networks

河蟹，學名中华绒螯蟹，俗称大闸蟹。河蟹养殖是中国很多地区实施精准扶贫、拉动经济增长、促进农民增收的重要突破口。溶解氧（Dissolved oxygen，DO）即溶解于水中的分子态氧，是集约化河蟹养殖成功与否的关键因素之一，其含量多少关乎河蟹的生长速度、发病率、死亡率，以及蟹塘中饲料的利用率和有害物质的产生量等。准确预测蟹塘中溶解氧的含量，有利于及时掌握溶解氧的变化趋势，提前采取防控措施，从而降低河蟹养殖风险，增加养殖经济效益，同时还对水质监测和疾病防控等生态问题具有预警意义。

近年来，随着机器学习和深度学习等技术的发展，越来越多的研究者将此类方法应用于水体溶解氧的预测研究中。刘双印等[1]采用支持向量机方法构建了基于蚁群优化的LSSVR溶解氧预测模型。宦娟等[2]提出基于K-means聚类和极限学习机（Extreme learning machine，ELM）结合的溶解氧预测模型，降低了不同趋势样本间的干扰，提升了预测准确度。Khan等[3]提出了模糊线性回归的溶解氧预测方法，与贝叶斯方法相比均方误差更低。吴慧英等[4]提出了主成分分析法（Principal component analysis， PCA）和SVR的池塘溶解氧预测模型，提取影响养殖水体溶解氧浓度的关键指标，降低模型输入变量的维度，提高了模型的训练速度。以上诸如支持向量机、K-means聚类等浅层的机器学习方法在有限样本和计算单元的情况下对复杂函数的表征学习能力有限，普遍缺乏长效性。

深度学习方法通过深层的非线性网络结构可以实现利用少量参数表示复杂函数，更有助于挖掘数据的内在信息，具有强大的数据学习能力和泛化能力。循环神经网络（Recurrent neural network， RNN）作为深度学习处理时间序列任务的经典网络结构，在时序数据预测中表现突出，但是随着序列长度的增加存在梯度爆炸或梯度消失风险，性能受到制约[5-6]。而基于RNN改进的长短时记忆网络（Long short-term memory， LSTM）[7]加入了细胞状态单元，较好地解决了长时间序列的依赖问题。有大量学者利用LSTM模型对时间序列进行预测的研究。温惠英等[8]利用遗传算法（GA）对LSTM的神经网络隐藏层数、训练次数、dropout等参数进行优化并利用高速公路交通流的数据进行验证，阐述了不同参数对LSTM模型调优过程中的影响。白盛楠等[9]在使用灰色关联度分析后搭建了基于LSTM的PM2.5预测模型，为空气污染的预警和治理提供了新的思路。魏昱洲等[10]利用双层LSTM网络结构，对风速数据进行了预测，证明超前10 min内各时间段的预测准确率达到了98.8%以上，具有很好的预测精度。也有少数学者利用LSTM模型对水体溶解氧进行了预测[11-13]，取得了一定成果。其中朱南阳等[14]在LSTM的基础上通过对低溶解氧权重的调节进行预测，在确保溶解氧趋势拟合的前提下提高了低浓度溶解氧的预测精度。陈英义等[15]提出主成分分析和LSTM相结合的溶解氧预测方法，试验证明LSTM模型的各项误差指标都优于其他浅层模型。

选择不同模型参数对LSTM模型预测性能的提升影响巨大。目前模型参数的选择往往过多依赖于研究者的经验和反复调试，需要大量的人力和计算资源。而粒子群优化算法（Particle swarm optimization，PSO）可以在保证模型评价指标最优的前提下，通过不断迭代寻优过程找到模型的最优参数，从而避免了依据经验选取参数而导致的预测精度低、调参时间长的问题。近两年，有少量学者开始尝试用PSO与LSTM相结合的方式对时间序列进行预测研究。杨孟达[16]提出改进PSO-LSTM模型对未来一天日均温度进行预测，试验结果表明PSO-LSTM模型有更好的准确性。刘可真等[17]利用PSO-LSTM模型对变压器中溶解气体浓度进行了预测，证明相较于传统预测方法，PSO-LSTM模型可以更好地追踪油中溶解气体浓度的变化规律。李万等[18]采用改进粒子群算法优化LSTM模型并对铁路客运量进行了预测。宋刚等[19]基于粒子群优化LSTM模型对各类股票的变化曲线进行了预测，证明了该模型具有普遍适用性。

本研究提出一种基于PSO-LSTM模型的蟹塘溶解氧预测方法，首先将LSTM模型中样本批次、隐藏层单元数、学习率、迭代次数等参数设为优化对象并给予取值范围，利用PSO算法根据参数范围初始化各粒子的位置信息并建立初始模型，将模型在验证集的预测误差作为粒子的适应度值不断更新，当满足最大迭代次数时停止更新优化，利用优化后的各类参数搭建LSTM预测模型对溶解氧进行预测。

1 材料与方法

1.1 数据采集

试验数据源自江苏省宜兴市高塍镇河蟹养殖基地，该基地内各池塘面积约为37 000 m2，水深约为1.2 m。每個池塘选取2～3个位置，每个位置分别选取距离水底30 cm、60 cm、90 cm处作为数据采集点布设传感器（图1）。

每个数据采集点设有溶解氧质量浓度、温度、浊度、pH、铵态氮质量浓度、电导率等传感器，传感器型号如表1所示。

试验所选取的数据为位置1-2（图1）的中层传感器采集的数据，采集时间为2020年4月11日至2020年5月24日，数据采集间隔时间为10 min，共采集到溶解氧质量浓度、温度、浊度、pH、铵态氮质量浓度、电导率等有效数据6 226条。其中5月8日采集的部分数据如表2所示。

分析长期监测数据后发现，蟹塘养殖水相关参数每小时内波动范围较小，其中溶解氧质量浓度和温度随着时间呈周期变化。水体溶解氧质量浓度在清晨和傍晚较高，而中午随着水温升高，尽管水草等植物光合作用增强，但是水中好氧因子也多，因此水中溶解氧质量浓度降低。除此之外，溶解氧质量浓度随着季节的不同也呈现明显的周期变化，而pH、铵态氮质量浓度、浊度、电导率等参数随溶解氧质量浓度的变化呈振荡变化特点，无明显的线性关系。

1.2 数据预处理与相关性分析

由于水下环境、设备腐蚀和人为干预等因素的影响，传感器的原始数据存在缺失值或异常值，在预处理阶段对获取到的6 226条原始数据采用均值法（公式1）对缺失值进行补充和异常值替换。

为了降低数据维度，筛选出与溶解氧质量浓度相关性较高的影响因子，采用SPSS工具的皮尔逊相关系数法（Pearson correlation coefficient）进行相关性分析。结果表明，溶解氧质量浓度与温度（相关系数-0.150**）、浊度（0.338**）、pH值（0.811**）、铵态氮质量浓度（-0.118**）具有显著相关性（P<0.01）， 而与电导率（-0.040）的相关性较低，因此选择温度、浊度、pH、铵态氮质量浓度等主要影响因子作为模型输入参数。

1.3 数据归一化

为了消除奇异样本数据，减少模型训练时间，通过公式（2）对数据进行归一化，将原数据映射到[0，1]之间。并将归一化后的数据按照8∶1∶1划分训练集、验证集和测试集。

1.4 模型构建

1.4.1 长短时记忆网络（LSTM） LSTM是一种特殊的RNN结构。为了解决传统RNN在长序列训练过程中的梯度弥散问题，LSTM引入了特殊的“门”结构。LSTM网络结构如图2所示，由输入门、遗忘门、输出门和细胞单元组成[7]。

图2中ft是遗忘門，决定上一时刻的细胞中有多少信息需要传递到当前时刻;it是输入门，用来控制当前单元嵌入细胞状态的程度;ot是输出门，输出门结合了细胞状态用来输出;Ct是记忆单元，用来记录不同门结构情况下细胞的状态;ht是输出。各个门之间的计算过程如下：

其中Wf，Wi，Wc，Wo是各个门的权重，bf，bi，bc，bo是各个门的偏置项。通过上述计算，LSTM可以利用门控单元进行长序列的信息传递，从而避免长期依赖问题。

1.4.2 粒子群优化算法（PSO） 粒子群优化算法的思想源于对鸟类觅食行为的研究，鸟群通过搜寻目前离食物最近的鸟的周围区域，利用个体的飞行经验判断食物所在并不断向集体共享信息，从而使得整个群体快速获得觅食路线的最优解[20]。PSO将群体中的个体看作在空间中进行搜索的粒子，每个粒子随机得到一组随机解，每个解都有特定的位置、速度和适应度，粒子在空间的搜寻过程中不断跟踪空间内最优解调整自身的参数，从而完成从局部最优到全局最优的搜索过程。

式中，ω为惯性权重，控制粒子在局部最优和全局最优中的权重分配;c1和c2为加速因子，用以调整飞行的步长，一般非负;r1和r2为值在[0，1]之间的随机数;Xkid，Vkid，Pkgd，Pkid分别对应该时刻下粒子的位置、速度、局部最优解和全局最优解。

1.4.3 粒子群优化算法优化LSTM模型参数流程 LSTM尽管在一定程度上解决了传统RNN的梯度弥散问题，但是由于门结构的加入增加了参数量，需要不断调整参数才能达到最优的效果。本研究利用粒子群优化算法对LSTM模型中样本批次、隐藏层单元数、学习率、迭代次数等参数进行寻优，确定溶解氧质量浓度预测模型的最佳参数。PSO-LSTM模型结构如图3所示：

算法流程：步骤1，将LSTM的样本批次、隐藏层单元数、学习率、迭代次数作为优化对象，根据预先设定的范围初始化粒子的位置信息。步骤2，初始化粒子群，划分训练集和测试集，并将步骤1中初始化参数输入LSTM网络进行训练，将模型预测误差作为粒子的适应度值。步骤3，比较每个粒子的适应度值及其经历过的最好位置，确定粒子的最优位置，并根据公式9和公式10更新粒子的速度和位置，计算新一轮粒子适应度值。步骤4，当搜寻过程达到预先设定的最大迭代次数，或粒子的适应度值不再随迭代次数明显变化时停止更新，并获得此时LSTM模型的样本批次、隐藏层单元数、学习率、迭代次数值。步骤5，将步骤4获得的各项数值输入LSTM模型进行训练和预测。

1.4.4 模型评价指标 为了验证PSO-LSTM模型对溶解氧质量浓度的预测性能，选取平均绝对百分比误差（MAPE）、均方根误差（RMSE）、均方误差（MSE）作为模型评价指标。各评价指标计算公式如下：

式中，N为预测的总次数，yi代表真实值，y^i代表预测值，MAPE表示预测值与真实值的百分误差，MSE反映了预测值与真实值之间偏差的期望值，RMSE是均方误差的算术平方根。

1.4.5 PSO-LSTM模型验证对比模型的选择 为了验证PSO-LSTM模型的有效性，选择单一LSTM模型、自回归移动平均模型（ARIMA）和低溶解氧预测模型（LDO-LSTM）作为对比模型。ARIMA模型是研究时间序列的重要模型，由自回归模型（AR）与滑动平均模型（MA）结合而成，仅需要对数据进行平稳性检验和差分即可搭建模型，具有适用范围广、预测误差小的特点。由于蟹塘溶解氧质量浓度偏低时危害更大，有学者通过更改损失函数的权重建立了LDO-LSTM模型提升低溶解氧时预测精度[10]，该模型根据溶解氧真实值在反向传播时给损失函数分配不同的权重，使网络更关注低溶解氧质量浓度时刻的特征，取得了良好的预测精度。

1.4.6 PSO-LSTM模型参数设置 本试验环境为Anaconda，编程语言为Python3.6，模型训练框架为基于Keras的Tensorflow1.4。LSTM模型的输入层神经元数量为4，隐藏层数量为1，输出层神经元数量为1，预测所需步长为40。训练过程中用Adam算法优化参数，将样本批次、隐藏层单元数、学习率、迭代次数设置为待优化参数，具体取值范围设置如下：样本批次取值范围为[4，128]，隐藏层单元数为[2，20]，学习率为[0.000 1，0.010 0]，迭代次数为[30，300]。粒子群优化算法参数设置为：粒子群数量为20，加速因子c1=c2=2，惯性权重ω设置为0.8，最大迭代次数为300。ARIMA中阶层（p）、阶数（q）和差分（d）分别设置为1、1、2。LSTM模型学习率设置为0.001，样本批次为32，迭代次数为100，隐藏层数量为1，每层神经元数量为10。LDO-LSTM模型的学习率为0.001，时间步长为10，输入层节点数为4，隐藏层节点数为20。

2 结果

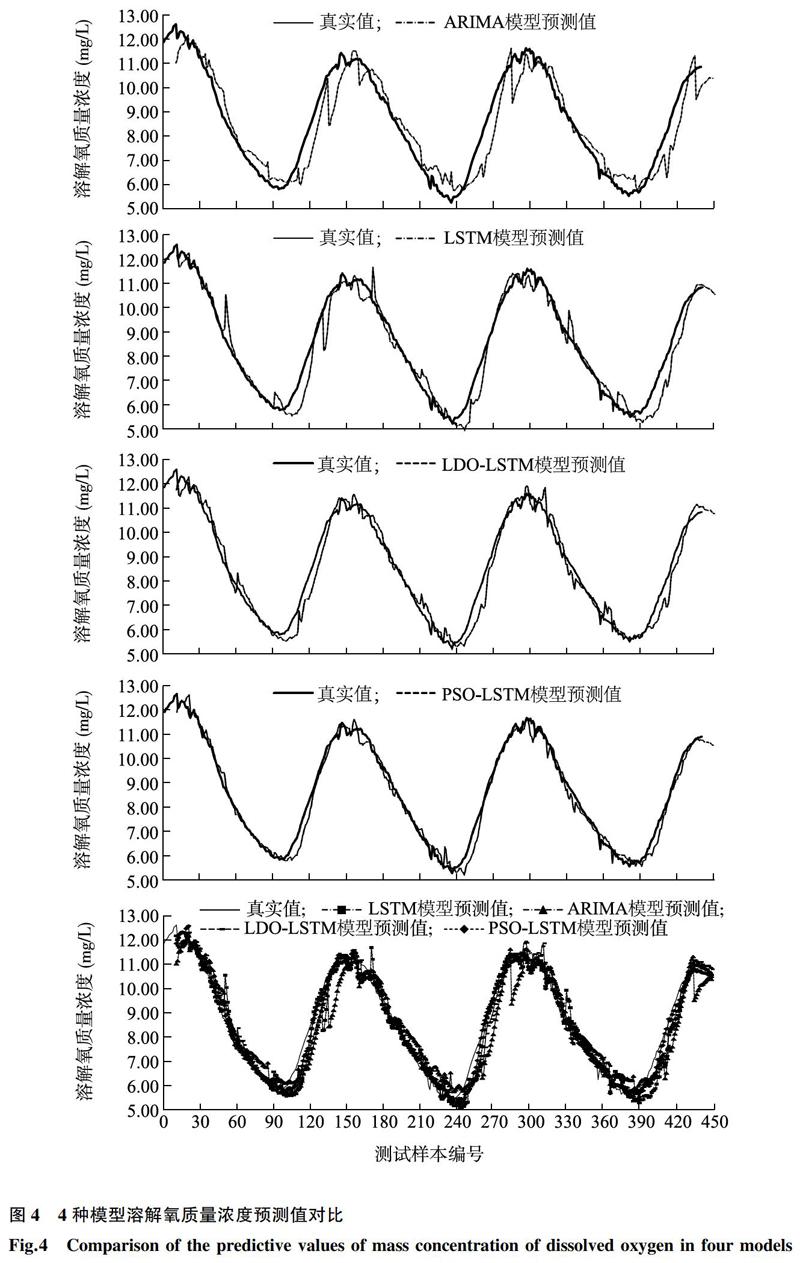
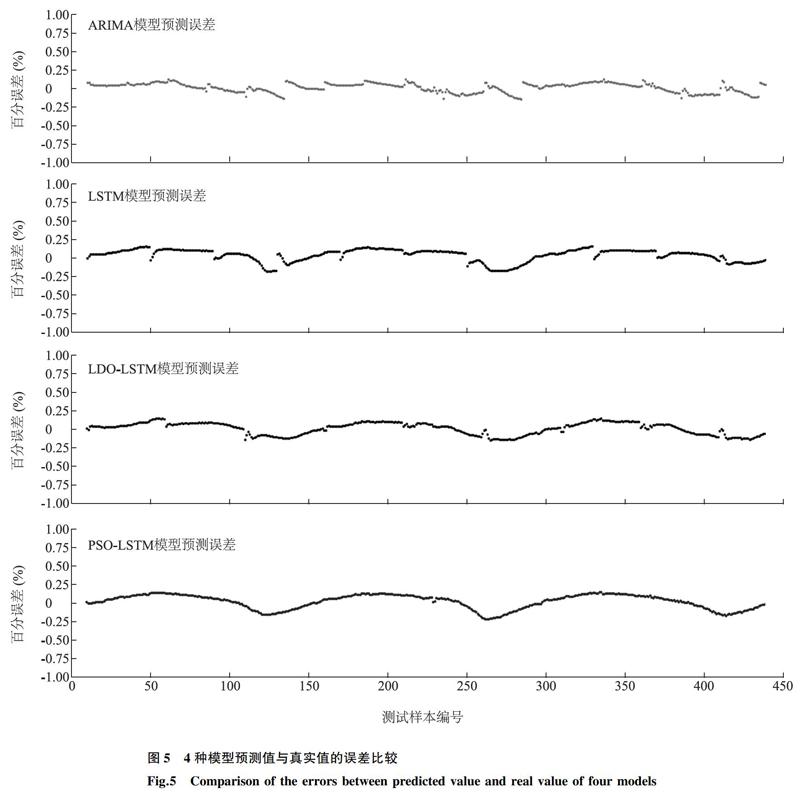
选取不同模型对蟹塘溶解氧质量浓度进行预测，各模型在测试集上的部分预测曲线和百分误差分别如图4、图5所示。

从图4可以看出，ARIMA模型在平滑区间的预测值与真实值曲线趋势基本拟合，但整体在时间上具有一定的滞后性，且部分点的预测值和真实值存在较大误差;LSTM模型相较于ARIMA模型减少了平均误差，具有更好的拟合曲线，但是在低质量浓度溶解氧的预测上普遍存在偏大的现象;而LDO-LSTM模型由于调整了在低溶解氧质量浓度时的权重分配，因此在继续保持了LSTM模型优点的基础上，还在低溶解氧质量浓度的预测上有较好的表现，但仍有部分时间段在时间上存在滞后性;PSO-LSTM模型相比较于其他模型在整体上曲线拟合和缩短时间滞后性上都得到了提升，预测值更贴近于真实值，说明PSO-LSTM模型比其他模型有更好的预测精度。

从图5可以看出，ARIMA、LSTM和LDO-LSTM模型部分相邻点的预测误差会出现“跳崖”现象，波动较大。而PSO-LSTM模型的预测误差曲线更加平滑，误差波动较小，具有很好的稳定性。

为了更加直观地反映各模型的预测效果，选择MSE、RMSE和MAPE 3个评价指标对4种模型进行评价（表3）。4种模型用于蟹塘溶解氧质量浓度预测的精度从高到低依次为PSO-LSTM模型、LDO-LSTM模型、LSTM模型和ARIMA模型。其中，PSO-LSTM模型的MSE、RMSE、MAPE值分别是0.013、0.114、0.354，与ARIMA模型相比MSE、RMSE、MAPE值分别降低了0.035、0.106、0.308，与单一的LSTM模型相比MSE、RMSE、MAPE值分别降低了0.016、0.058、0.18，与LDO-LSTM模型相比MSE、RMSE、MAPE值分别降低了0.009、0.035、0.116。可见，利用PSO进行參数优化后的LSTM模型在溶解氧质量浓度预测上整体表现突出，预测值和真实值之间的偏差小，准确性和稳定性提升明显。

为了进一步比较不同模型在连续性预测中的表现，选取测试集中未来连续10个时间点的预测值和真实值进行比较分析，结果如表4所示。可以看出，PSO-LSTM模型在测试集连续10个时间点中单值最大误差为1.496%，而LDO-LSTM、LSTM和ARIMA模型的最大误差分别为4.959%、3.140%，和7.245%。另外PSO-LSTM模型在10个采集点的平均绝对误差为0.658%，相较于LDO-LSTM、LSTM和ARIMA等模型的误差分别降低了2.550个百分点、1.891个百分点、4.055个百分点，证明PSO-LSTM模型在连续性、长期性的蟹塘溶解氧质量浓度预测方面具有很高的准确性，对于溶解氧质量浓度变化情况的提前预警和调控具有重要意义。

3 讨论

本研究针对采集到的蟹塘水质数据先进行变量间皮尔逊相关性分析，确定影响溶解氧质量浓度的主要变量，再结合目前主流的时间序列模型LSTM，利用粒子群优化算法优化LSTM模型的超参数，根据优化结果搭建PSO-LSTM模型研究蟹塘溶解氧质量浓度变化规律。通过试验对比发现：（1）对数据进行相关性分析可以有效降低训练数据的维度，减少训练时间，提升预测精度。（2）LSTM网络模型能较好地解决ARIMA模型在溶解氧质量浓度预测中的滞后性问题，并且提高准确性。（3）PSO-LSTM模型的精度较单一的LSTM有明显提升，说明参数的优化对模型预测精度具有较大影响。（4）相比于ARIMA、LSTM、LDO-LSTM模型，PSO-LSTM模型的预测值和真实值之间的偏差小，准确性和稳定性提升明显，尤其是PSO-LSTM模型在未来一个时间点和多个时间点的预测精度优于其他模型，能够较好地应用于蟹塘溶解氧质量浓度的预警预报。

综上所述，基于PSO-LSTM模型预测蟹塘溶解氧质量浓度具有较好的预测精度，可以在蟹塘水质预警、水质环境监测、溶解氧质量浓度自动精准调控等方面发挥作用。但是在试验过程中仅考虑了水体内部不同因子对溶解氧质量浓度的影响，并没有考虑气压、风速等外在环境因素，在未来的实际应用中需要对数据进行更全面的整合与分析，进一步提升预测的准确性和稳定性。

参考文献：

[1] 刘双印，徐龙琴，李道亮，等. 基于蚁群优化最小二乘支持向量回归机的河蟹养殖溶解氧预测模型[J].农业工程学报，2012，28（23）：167-175.

[2] 宦 娟，刘星桥. 基于K-means聚类和ELM神经网络的养殖水质溶解氧预测[J].农业工程学报，2016，32（17）：174-181.

[3] KHAN V C. Comparing A Bayesian and fuzzy number approach to uncertainty quantification in short-term dissolved oxygen prediction[J]. Journal of Environmental Informatics， 2017， 30（1）：1-16.

[4] 吴慧英，杨日剑，张 颖，等. 基于PCA-SVR的池塘DO预测模型[J].安徽大学学报（自然科学版），2016，40（6）：103-108.

[5] BENGIO Y， SIMARD P， FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks， 1994， 5（2）： 157-166.

[6] 杨 丽，吴雨茜，王俊丽，等. 循环神经网络研究综述[J].计算机应用，2018，38（S2）：1-6，26.

[7] HOCHREITER S， SCHMIDHUBER J. Long short-term memory[J]. Neural Computation， 1997， 9（8）： 1735-1780.

[8] 温惠英，张东冉，陆思园. GA-LSTM模型在高速公路交通流预测中的应用[J].哈尔滨工业大学学报，2019，51（9）：81-87，95.

[9] 白盛楠，申晓留. 基于LSTM循环神经网络的PM_（2.5）预测[J].计算机应用与软件，2019，36（1）：67-70，104.

[10]魏昱洲，许西宁. 基于LSTM长短期记忆网络的超短期风速预测[J].电子测量与仪器学报，2019，33（2）：64-71.

[11]LIU S Y， XU L Q， LI D L. Prediction of dissolved oxygen content in river crab culture based on least squares support vector regression optimized by improved particle swarm optimization[J]. Computers and Electronics in Agriculture， 2013， 95：82-91.

[12]TA X X， WEI Y G. Research on a dissolved oxygen prediction method for recirculating aquaculture systems based on a convolution neural network[J]. Computers and Electronics in Agriculture， 2018， 145： 302-310.

[13]LIU Y Q，ZHANG Q，SONG L H. Attention-based recurrent neural networks for accurate short-term and long-term dissolved oxygen prediction[J]. Computers and Electronics in Agriculture，2019，165：1-11.

[14]朱南陽，吴 昊，尹达恒，等. 基于长短时记忆网络（LSTM）的蟹塘溶解氧估算优化方法[J].智慧农业，2019，1（3）：67-76.

[15]陈英义，程倩倩，方晓敏，等. 主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧[J].农业工程学报，2018，34（17）：183-191.

[16]杨孟达. 基于改进PSO-LSTM神经网络的气温预测[J].现代信息科技，2020，4（4）：110-112.

[17]刘可真，苟家萁，骆 钊，等. 基于PSO-LSTM模型的变压器油中溶解气体浓度预测方法[J]. 电网技术，2020，44（7）：2778-2785.

[18]李 万，冯芬玲，蒋琦玮. 改进粒子群算法优化LSTM神经网络的铁路客运量预测[J].铁道科学与工程学报，2018，15（12）：3274-3280.

[19]宋 刚，张云峰，包芳勋，等. 基于粒子群优化LSTM的股票预测模型[J].北京航空航天大学学报，2019，45（12）：2533-2542.

[20]李爱国，覃 征，鲍复民，等. 粒子群优化算法[J].计算机工程与应用，2002（21）：1-3，17.

（责任编辑：张震林）